РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ ВТОРОЙ СТЕПЕНИ

 9 класс     Урок №_______________________________________________________________
Решение систем уравнений второй степени
Цели урока:

• обобщить и систематизировать знания учащихся по теме урока ; подготовить учащихся к написанию самостоятельной  работы.
• Развитие монологической речи учащихся, логического мышления;
• Воспитание интереса к математике.

Задачи урока.

·         обобщить и систематизировать знания учащихся о способах решения систем уравнений второй степени. ;создать условия для самооценки своих возможностей, атмосферу заинтересованности каждого ученика в результатах деятельности;

• развивать познавательную активность, навыки индивидуальной и самостоятельной работы

Тип урока: Урок обобщения и систематизации знаний.

Ход урока

I. Организационный момент.

II. Устная работа. (Подготовка к ОГЭ)Решите систему уравнений способом сложения:

а) 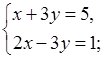                       б)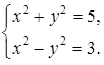

III. Формирование умений и навыков. Все задания разбиты на две группы

IV. Итоги урока.

В о п р о с ы   у ч а щ и м с я:

– Что называется решением системы уравнений?

– Опишите способ подстановки решения систем уравнений второй степени.

– Опишите алгоритм решения систем уравнений второй степени способом сложения.

– Любое ли уравнение второй степени можно решить способом подстановки? способом сложения?

Домашнее задание_____________________________________________Д о п о л н и т е л ь н о: № 438.

9 класс Урок №_______________________________________________________________________
Тема урока:      решения задач       с помощью систем уравнений

Цели урока

·         рассмотреть, как могут решаться текстовые задачи с помощью систем  уравнений  второй  степени;  формировать  умение  решать  такие задачи:

·         Развитие монологической речи учащихся, логического мышления;

• Воспитание интереса к математике.

Задачи урока.

·         рассмотреть, как могут решаться текстовые задачи с помощью систем  уравнений  второй  степени;  формировать  умение  решать  такие задачи:

·         обобщить и систематизировать знания учащихся о способах решения систем уравнений второй степени. ;создать условия для самооценки своих возможностей, атмосферу заинтересованности каждого ученика в результатах деятельности;

• развивать познавательную активность, навыки индивидуальной и самостоятельной работы

Тип урока: урок усвоения новых знаний.

Ход урока

I.      Организационный момент.

II.   Проверка домашней работы .СР по текстам . аналогичным ДР

III.             Устная работа.

Решите систему уравнений:

а) 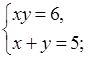                                 б)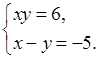

IV.Актуализация опорных знаний

V.   Объяснение нового материала.  

Учащиеся уже умеют применять системы линейных уравнений для решения текстовых задач. Поэтому главным при изучении данного материала будет обобщение и систематизация их знаний о решении таких задач, а также закрепление методов решения систем уравнений второй степени.

Для демонстрации принципа решения задач с помощью систем уравнений второй степени достаточно привести пример из учебника.

V1. Формирование умений и навыков. Цель: На этом уроке главное, чтобы учащиеся усвоили схему решения задач с помощью систем уравнений второй степени. Необходимо дать им под запись примерный план, согласно которому можно осуществлять решение таких задач. На первых порах необходимо, чтобы учащиеся вслух комментировали решение задач согласно записанному плану

Схема решения задач с помощью систем

 уравнений второй степени

1. Прочитать условие задачи и понять его.

2. Указать объекты, о которых идет речь в задаче.

3. Одну из величин обозначить за х, а другую – за у.

4. Составить систему уравнений по условию задачи.

5. Решить эту систему уравнений.

6. Интерпретировать полученные результаты.

.

№ 460.

Р е ш е н и е

1) В условии речь идет о прямоугольном треугольнике. Требуется найти его площадь.

2) Известна гипотенуза треугольника и его периметр. Для нахождения площади нужно знать его катеты.

3) Обозначим  один  катет  треугольника  через  х  см,  а  другой –  через у см.

4) Зная периметр треугольника, составим уравнение: х + у +37 = 84.

По теореме Пифагора составим второе уравнение: х² + у² = 37².

Получим систему уравнений:

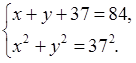
5) Решим эту систему уравнений способом подстановки:

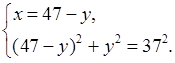
47² – 94у + у² + у² – 37² = 0;

2у² – 94у + (47 – 37) (47 + 37) = 0;

2у² – 94у + 10 · 84 = 0;

у² – 47у + 420 = 0;

у₁ = 35   х₁ = 12;

у₂ = 12   х₂ = 35.

6) Получаем, что катеты треугольника равны 12 см и 35 см. Найдем его площадь: S= a . b

S =  · 12 · 35 = 210 (см²).           

 О т в е т: 210 см².

3. № 463.        При решении этой задачи учащимся поможет рисунок, сделанный согласно ее условию.

Пусть стороны прямоугольника равны х см и у см. Учитывая, что его площадь равна 30 см², получим уравнение: ху = 30.S₁ = х² см², S₂ = у² см².Получим уравнение 2х² + 2у² = 122 или  х² + у² = 61.

Составим систему уравнений:

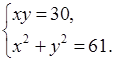Находим ее решения: (–6; –5), (6; 5), (–5; –6), (5; 6).

Первое и третье решения не подходят по условию задачи. Значит, стороны прямоугольника равны 5 см и 6 см.      О т в е т: 5 и 6 см.

V. Итоги урока.

В о п р о с ы   у ч а щ и м с я:

– Какие  существуют  способы  решения  систем  уравнений  второй степени?

– В чем заключается каждый из этих способов?

– Опишите  план  решения  текстовой  задачи  с  помощью  системы уравнений.

Домашнее задание: № 456, № 458, № 459.

9 класс Урок №___________________________________________________Решение задач с помощью
систем уравнений второй степени

Цели урока формировать умение решать задачи на движение с помощью систем уравнений второй степени рассмотреть, как могут решаться текстовые задачи с помощью систем  уравнений  второй  степени;  формировать  умение  решать  такие задачи: Развитие монологической речи учащихся, логического мышления;Воспитание интереса к математике.

Задачи урока. рассмотреть, как могут решаться текстовые задачи с помощью систем  уравнений  второй  степени;  формировать  умение  решать  такие задачи:обобщить и систематизировать знания учащихся о способах решения систем уравнений второй степени. ;создать условия для самооценки своих возможностей, атмосферу заинтересованности каждого ученика в результатах деятельности;развивать познавательную активность, навыки индивидуальной и самостоятельной работы

Тип урока: урок усвоения новых знаний.

Ход урока

VI.Организационный момент.

VII.          Проверка домашней работы

Устная работа. Периметр прямоугольника равен 20 см, а его площадь равна 21 см². Пусть х и у – стороны этого прямоугольника. Какая из систем соответствует условию задачи?

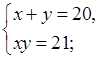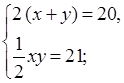а) б) в)

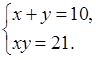
III. Проверочная работа.

IV. Формирование умений и навыков. Сначала необходимо актуализировать знания учащихся о решении задач на движение, выделив  р я д   э т а п о в.

1) Анализ условия:

– Какие объекты рассматриваются в задаче?

– Какое движение описано в задаче (однонаправленное, движение навстречу, по кругу и т. д.)?

– Значения каких величин известны?

2) Выделение процессов, которые описаны в задаче.

3) Выбор неизвестных величин и заполнение таблицы.

4) Составление системы уравнений.

5) Решение системы уравнений.

6) Интерпретация и проверка полученного решения.

Как реализуются описанные этапы, можно разобрать на примере задачи № 472.

Р е ш е н и е

1) В задаче описано движение двух пешеходов навстречу друг другу. Известно расстояние между пунктами и расстояние, которое прошли пешеходы за 4 часа.

2) Выделим два процесса:

– реальное движение пешеходов;

– движение при условии выхода одного из пешеходов на 1 ч раньше.

3) Пусть х км/ч – скорость первого пешехода и у км/ч – скорость второго пешехода.

Заполним две таблицы:

4) Известно, что расстояние от А до В равно 40 км, поэтому получим уравнение: 4х + 4у = 36. Известно, что при движении с заданным условием первый пешеход был в пути на 1 ч дольше, то есть получим уравнение: 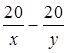 = 1. Составим систему уравнений:

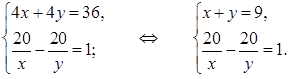 5) Решим ее способом подстановки: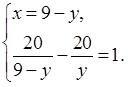

20у – 20 (9 – у) – у (9 – у) = 0; 20у – 180 + 20у – 9у + у² = 0; у² + 31у – 180 = 0; у₁ = 5    х₁ = 9 – 5 = 4;

у₂ = – 36 (не подходит по смыслу задачи).

6) Получаем скорости  пешеходов: 4 км/ч и 5 км/ч.         О т в е т: 4 и 5 км/ч.

Упражнения: 1. № 473, № 547.(индивидуальные задания)

2. № 461. (коллективное решение)

Р е ш е н и е

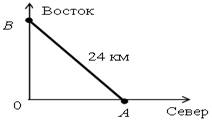
Пусть х км/ч – скорость первого отряда и у км/ч – скорость второго отряда.

Заполним таблицу:

Известно, что первый отряд прошел на 4,8 км больше, чем второй. Получим уравнение:

4х – 4у = 4,8. На рисунке ОА = 4х и ОВ = 4у. По теореме Пифагора, получим уравнение:

(4х)² + (4у)² = 24².  Составим систему уравнений:

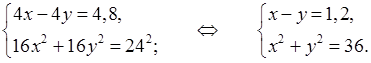 Решая  систему  способом  подстановки, находим, что х = 4,8 и у = 3,6 (другое решение является отрицательным). О т в е т: 4,8 и 3,6 км/ч.

Сильным в учебе учащимся можно дополнительно дать выполнить № 548.

Р е ш е н и е

Пусть  х км/ч  –  скорость  первого  автомобиля,  а у км/ч  –  скорость второго.

В первую таблицу занесем данные о прохождении каждым автомобилем всего пути, а во вторую – об их движении после встречи.

Поскольку после встречи первый автомобиль приходит в N через 1,25 ч, а второй в М через 0,8 ч, то первый на весь путь тратит на 1,25 – 0,8 = 0,45 ч больше. Получим уравнение:

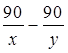 = 0,45. После встречи первый автомобиль проходит 1,25х км, а второй – 0,8у км. Получим уравнение: 1,25х + 0,8у = 90.

Составим систему:

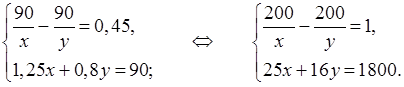
Решая эту систему, находим, что х = 40 и у = 50.

О т в е т: 40 км/ч и 50 км/ч.

V. Итоги урока.

В о п р о с ы   у ч а щ и м с я:

– Опишите различные способы решения систем уравнений второй степени.

– Перечислите этапы решения задач на движение.

– Какие виды движения могут описываться в задаче?

– В чем заключается интерпретация полученного решения?

Домашнее задание: № 462, № 474. Д о п о л н и т е л ь н о: № 549.

Скачано с www.znanio.ru