Решение тригонометрических уравнений

“Приобретать знания - храбрость, приумножать их - мудрость, а умело применять - великое искусство”.

Восточная мудрость

Тема: Решение тригонометрических уравнений.

Цели и задачи урока:

     1. Образовательные:

 - закрепление программных знаний и умений по решению тригонометрических уравнений;

- обобщение и систематизация материала;

-  создание  условий для  контроля и самоконтроля  усвоения знаний и умений;

- установление межпредметных связей.

     2. Воспитательные:

- воспитание навыков делового общения, активности;

-формирование интереса к математике и ее приложениям.

    3. Развивающие:

- формирование умений применять приемы: сравнения, обобщения, выделения главного, переноса знаний в новую ситуацию,

- развитие познавательного интереса, математического кругозора, мышления и речи, внимания и памяти.

 

Формы организации работы учащихся на уроке:

индивидуальная, фронтальная, парная.

Оборудование: ноутбук, мультимедийный проектор, презентация.

Ход урока

I. Организующее начало урока

- Сегодня у нас не совсем обычный урок. У нас присутствуют гости, и я надеюсь, что мы не разочаруем.

И начать урок мне хочется тоже не совсем обычно.

Презентация

Слайд 1

- Французский математик и физик Паскаль говорил: “Предмет математики настолько серьезен, что полезно не упускать случаев делать его намного занимательным”.

Я решила начать последовать совету Паскаля и предложить вам разгадать такой ребус.

Слайд 2

- Как вы думаете, почему я предложила вам расшифровать такое слово? Что оно означает?

Слайд 3

“Тригонометрия” происходит от греческого слова τριγουο треугольник и греческого μετρειν измерять, т.е. означает измерение треугольников. Тригонометрия - это раздел математики, в котором изучаются тригонометрические функции и их приложения к геометрии.

- Одной из наиболее важных тем тригонометрии является решение тригонометрических уравнений, с которыми мы познакомились в этом учебном году. Эта тема очень актуальна и важна, т.к. входит в вопросы переводного экзамена в 10 кл. и широко представлена на ЕГЭ в 11 кл.

Итак, тема сегодняшнего урока “Решение тригонометрических уравнений”.

II Актуализация знаний

Слайд 4. “Решение тригонометрических уравнений”.

Слайд 5

Восточная мудрость гласит: “Приобретать знания - храбрость, приумножать их - мудрость, а умело применять - великое искусство”

Какие-то знания по теме “Тригонометрические уравнения” мы уже приобрели, приумножать знания - никогда не поздно, поэтому и на сегодняшнем уроке будем мудрыми, и еще раз посмотрим, насколько умело мы применяем наши знания.

Чтобы решить любое тригонометрическое уравнение, что необходимо знать?

- Общие формулы решения простейших тригонометрических уравнений.

- Какие простейшие тригонометрические уравнения вы знаете?

- sin x = a, cos x = a, tg x = a, ctg x = a.

- Вспомните общие формулы их решений.

Слайд 6

Простейшие тригонометрические уравнения sin x = a, cos x = a

- Что надо помнить при решении таких уравнений?

- Частные случаи. Слайд 7

Слайд 8

Уравнения вида tg x = a и ctg x = a.

- Проверим, насколько хорошо мы умеем решать простейшие тригонометрические уравнения.

Укажите общую формулу, по которой находятся все корни уравнения. Слайд 9. (Для удобства - задания на листах на каждом столе)

Вариант I

1) 

А) ,

Б) ,

В) Корней нет,

Г) ,

Д) .

Ответ: А), Г)

2) 

А) ,

Б) ,

В) ,

Г) Корней нет,

Д) .

Ответ: В).

Вариант II

1) 

А) ,

Б) ,

В) ,

Г) ,

Д) 

Ответ: В).

2) 

А) ,

Б) 

В) 

Г) ,

Д) .

Ответ: А), В).

Слайд 10

Проверьте себя! (Указаны правильные ответы).

- Поднимите руку, кто не допустил ни одной ошибки.

III. Основная часть урока

- Решение простейших уравнений мы вспомнили, можно приступать к решению более сложных уравнений.

Вспомним, какие методы тригонометрических уравнений мы знаем.

Наверное, надо начать с общих методов:

- разложение на множители,

- метод введения новой переменной,

- графический метод,

- решение однородных уравнений 1-ой и 2-ой степени

Сегодня мы будем работать над решением этих уравнений. Некоторые решим устно, более сложные - письменно.

Слайд 11

1. .

- Метод?

- Введение новой переменной (у = sin х)

Слайд 12

2. 

- Сведение к квадратному уравнению относительно cos x.

Слайд 13

3. 

- Как называется такое уравнение и как его решить?

- Однородное II степени : cos² x 0

Сведение квадратному уравнению относительно tg.

4. Укажите число корней уравнения  на промежутке [0; 2π]

- Какой метод решения удобно использовать?

- Графический.

- А теперь решим следующие уравнения письменно (сразу 2 человека на боковых досках).

5. 

Упростим левую часть уравнения:

, 

 - посторонний корень

6.Каким методом воспользуемся?

(Вынесением за скобки общего множителя)

- А можно поделить на соsx? Давайте проверим (к доске идут 2 ученика выполняют двумя способами)

1)2COS²X-COSX=0                                  2) )2COS²X-COSX=0 :COSX

                                                                     2cosx-1=0

                                                                     Cosx=1/2

COS X (2COSX-1)=0                                     x=        

 X=

.

Решение прикладной задачи

      Учитель: «Решение прикладных задач помогает формировать представление о роли математики в изучении окружающего мира, видеть разницу между реальным и идеальным, между физическим явлением и его математической моделью.

      О прикладной направленности изучаемой темы расскажет ученик, который подготовил физическую задачу».

 

    Задача. Под каким углом  должен плыть пловец, чтобы из точки  А попасть в точку , если скорость пловца , скорость течения реки , ? (см. рис к задаче).

 

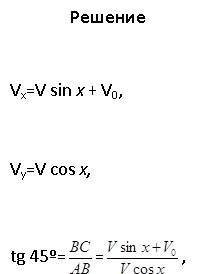
=1,

cos x – sin x=1,

               sin ( - x) - sin x = 1,

               2 sin ( - x) cos = 1,

                sin(x - )= -,

                 x = 2 πn, n∈Z;                             

                 x = – +2 πn, n∈Z.

 

 

 

Учитель: «Решение проведено в общем виде, применительно к реальным явлениям

 x =0°».

 

Вывод:

Решение упражнений на систематизацию уравнений.

        Ученикам предлагаются блоки уравнений на сравнение, обобщение, выделение главного.

1.      Что бы это значило?

 

Нельзя?!

1) sin x + cos x = 0

2) sin2 x - 5 sin x cos x + 6 cos2 x = 0

3) 4 sin x cos x - cos2 x= 0

Можно ?!

 

     

Ответ: 1 - однородное уравнение первой степени, решается методом деления

на  cos x (sin x);

                  2 - однородное уравнение второй степени, решается методом деления

на  cos² x (sin² x);

                     3 -  нельзя  делить  на cos² x,  это приведет к потере корней.

 

IV. Постановка домашнего задания

 

 

V. Рефлексия

При подведении итога урока мне хочется задать вам один вопрос: что бы вы посоветовали ученику, который только начинает учиться решать тригонометрические уравнения?

Начните свои советы со слов: “Помни, что…”.

И в конце нашего урока хочу обратить ваше внимание на такие слова Станислава Коваля “Уравнение - это золотой ключ, открывающий все математические сезамы”.

Слайд 28

Спасибо за урок!