Решение уравнений вида х2

Решение уравнений вида х² = а                      17.11.2021г.

Цели: рассмотреть вопрос о количестве корней уравнения х² = а и формировать умение решать такие уравнения.

Задачи урока:

·         рассмотреть решение квадратного уравнения вида х² = а.

·         научить применять умения преобразовывать выражения, содержащие квадратные корни;

·         поддержать интерес учащихся к математике с целью совершенствования вычислительных навыков;

·         отработать умение находить арифметический квадратный корень из числа.

Ход урока

I.                    Организационный момент.

Приветствие учащихся. Проверка готовности учащихся к работе.

Актуализация опорных знаний.

II. Устная работа.

– Вычислите:

а) ;        б) ;        в) ;        г) ;        д) ;

е) 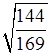;        ж) 0,3²;        з) (–0,3)²;        и) ;        к) .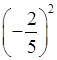

III. Объяснение нового материала.

Желательно, чтобы учащиеся самостоятельно решили вопрос о возможном количестве корней уравнения вида х² = а.

Для этого сначала можно предложить им выполнить следующее задание: какие числа можно вписать в пустые карточки, чтобы равенство было верным?

а) ² = 25;                              б) ² = ;             в) ² = –9;

г) ² = ;              д) ² = 0;                           е) ² = .

Затем перейти к уравнению х² = а и предложить учащимся сформулировать утверждение о различных случаях, возникающих при поиске корней таких уравнений.

На доску можно вынести  з а п и с ь:

После этого перейти к графической интерпретации решения уравнения х² = а. Сделать вывод, что если а > 0, то корнями уравнения х² = а будут числа  и  –.

IV. Формирование умений и навыков.

1. № 319, № 320.

2. № 321 (а, в).

3. Даны уравнения:

х² = 16,        х² = –100,        х² = 5,        х² = 0,        х² = .

Выберите из них те, которые:

а) имеют два корня;

б) имеют два рациональных корня;

в) имеют два иррациональных корня;

г) имеют один корень;

д) не имеют корней.

4. № 322.

5. Составьте какое-нибудь уравнение, имеющее корни:

а) 7 и –7;             б) 0,2 и –0,2;            в)  и  –.

Необходимо, чтобы учащиеся составили к каждому случаю несколько уравнений. Можно устроить своеобразное соревнование: у кого из них получится больше различных уравнений.

Н а п р и м е р, в первом случае можно составить такие уравнения:

х² = 49,        2х² = 98,        х² + 1 = 50,        10 – х² = –39 и т. п.

6. № 324 (а, в).

О б р а з е ц   о ф о р м л е н и я:

а) (х – 3)² = 25

О т в е т: –2; 8.

V. Итоги урока.

В о п р о с ы   у ч а щ и м с я:

– Что называется арифметическим квадратным корнем из числа?

– Может ли в выражении  число а быть отрицательным? Почему?

– Сколько корней может иметь уравнение х² = а? От чего это зависит?

– Какие корни имеет уравнение х² = а, если а > 0? а = 0?

Домашнее задание: № 321 (б, г), № 323, № 324 (б, г).