
9.1. Методика поиска решения в MS Excel
Для решения задач оптимизации в MS Excel используют надстройку Поиск решения, которая вызывается из пункта главного меню «Сервис» (рис. 9.1).
Рис. 9.1.
Если в версии Excel, установленной на Вашем компьютере, отсутствует данный подпункт меню «Сервис», необходимо вызвать пункт меню «Надстройки» и в предложенном списке дополнительных модулей выбрать «Поиск решения» (рис. 9.2).
Рис. 9.2.
Рассмотрим на примере использование данной надстройки. Решим с её помощью задачу, математическая модель которой строилась в примере 1.1. Математическая модель задачи имеет вид:
![]()
![]()
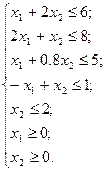
Составим шаблон в редакторе Excel, как показано на рис. 9.3.
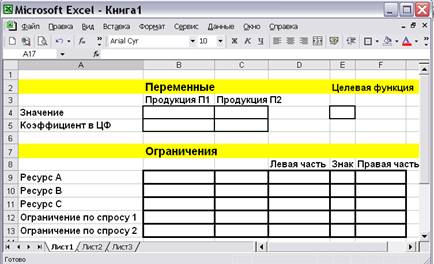
Рис. 9.3. Шаблон оформления задачи.
Теперь занесём данную в задаче числовую информацию (рис.9.4).
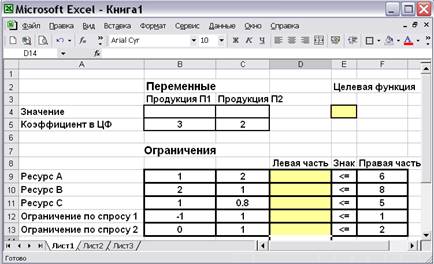
Рис.9.4. Исходные данные задачи
В выделенные пустые ячейки (значения целевой функции и левых частей неравенств) необходимо занести формулы, отображающие связи и отношения между числами на рабочем листе.
Ячейки B4 – С4 называются в Excel изменяемыми (в нашей модели это неизвестные переменные), т.е., изменяя их Поиск решения будет находить оптимальное значение целевой функции. Значения, которые первоначально вводят в эти ячейки, обычно нули (незаполненные клетки трактуются по умолчанию как содержащие нулевые значения).
Теперь необходимо ввести формулы. В нашей математической модели, целевая
функция представляет собой произведение вектора коэффициентов на вектор
неизвестных. Действительно, выражение ![]() можно
рассматривать как произведение вектора (3,2) на вектор
можно
рассматривать как произведение вектора (3,2) на вектор ![]() .
.
В Excel существует функция СУММПРОИЗВ, которая
позволяет найти скалярное произведение векторов. В ячейку Е4 необходимо вызвать
данную функцию, а в качестве перемножаемых векторов задать адреса ячеек,
содержащих коэффициенты уравнений (в данном случае, это В5:С5) и ячеек, в
которые в результате решения будут помещены значения ![]() (ячейки
В4:С4) (рис. 9.5).
(ячейки
В4:С4) (рис. 9.5).
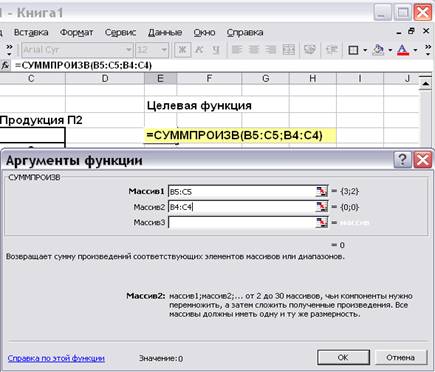
Рис. 9.5. Вызов функции СУММПРОИЗВ.
Каждая левая часть ограничения тоже представляет собой произведение двух
векторов: соответствующей строки матрицы затрат и вектора неизвестных. То
есть, выражение ![]() (для первого
ограничения
(для первого
ограничения ![]() ) будем рассматривать как
произведение вектора коэффициентов (1,2) и вектора пока переменных
) будем рассматривать как
произведение вектора коэффициентов (1,2) и вектора пока переменных ![]() .
.
В ячейке, отведенной для формулы левой части первого ограничения (D9), вызовем функцию СУММПРОИЗВ. В качестве адресов перемножаемых векторов занесем адрес строки коэффициентов В9:С9 и адрес значений переменных В4:С4 (рис. 9.6).
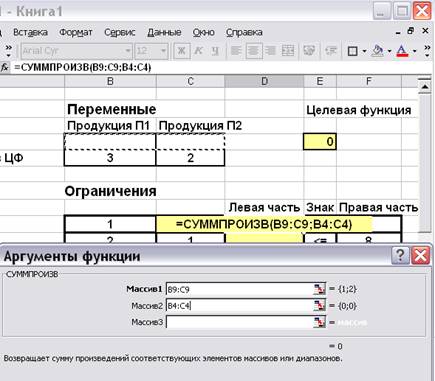
Рис. 9.6
В четыре оставшиеся ячейки графы «Левая часть» вводим аналогичные формулы, используя соответствующую строку матрицы затрат. Фрагмент экрана с введёнными формулами показан на рис.9.7.
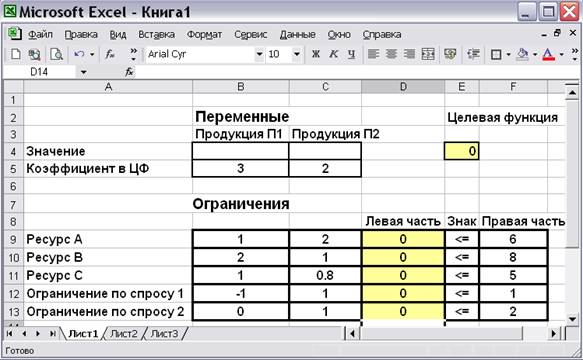
Рис. 9.7
Важно! К моменту вызова сервиса «Поиск решения» на рабочем листе с задачей должны быть занесены формулы для левых частей ограничений и формула для значения целевой функции.
В меню Сервис выбираем Поиск решения. В появившемся окне задаём следующую информацию:
1. в качестве целевой ячейки устанавливаем адрес ячейки для значения целевой функции Е4;
2. «флажок» устанавливаем на вариант «максимальному значению», т.к. в данном случае, целевая функция дохода подлежит максимизации;
3. в качестве изменяемых ячеек заносится адрес строки значений переменных В4:С4;
4. справа от окна, предназначенного для занесения ограничений, нажимаем кнопку «Добавить», появится форма для занесения ограничения (рис. 9.8)
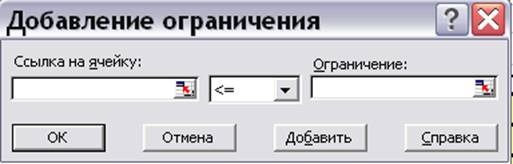
Рис.9.8. Форма для занесения одного ограничения ЗЛП.
5. в левой части формы «Ссылка на ячейку» заносится адрес формулы для левой части первого ограничения D9, выбирается требуемый знак неравенства (в нашем случае, <=), в поле «Ограничение» заносится ссылка на правую часть ограничения F9 (рис. 9.9).
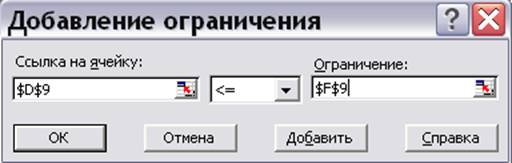
Рис.9.9. Занесение первого ограничения задачи.
Аналогично заносятся все ограничения задачи, после чего нажимается кнопка «ОК».
Таким образом, окно «Поиск решения» с занесенной информацией выглядит следующим образом (рис.9.10):
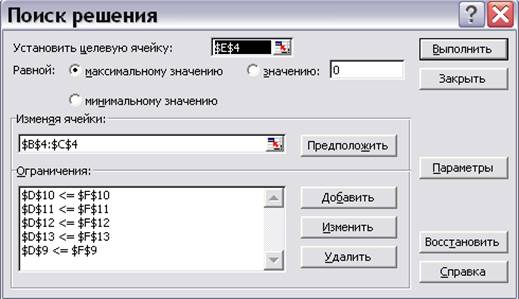
Рис. 9.10.
Далее необходимо нажать кнопку Параметры, установить «флажки» «Линейная модель» и «Неотрицательные значения», поскольку в данном случае задача является ЗЛП, а ограничение 6) требует неотрицательности значений (рис.9.11).
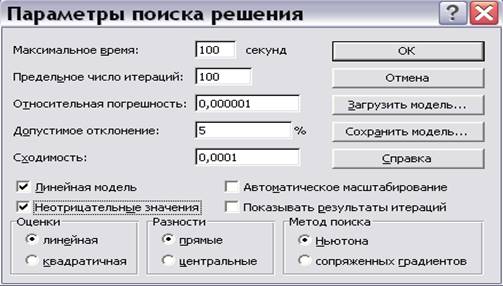
Рис. 9.11. Установка параметров
Затем следует нажать «ОК», «Выполнить», после чего появляется окно результата решения (рис.9.12).
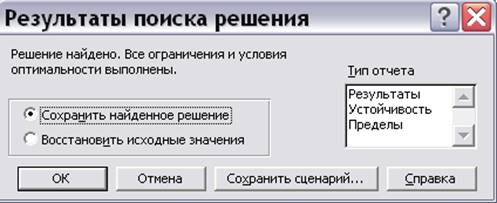
Рис. 9.12. Окно результата решения
Если в результате всех действий получено окно с сообщением «Решение найдено», то Вам предоставляется возможность получения трех типов отчета, которые полезны при анализе модели на чувствительность. В данном примере достаточно сохранить найденное решение, нажав «ОК». В результате получено решение задачи из примера 1.1. (рис.9.13).
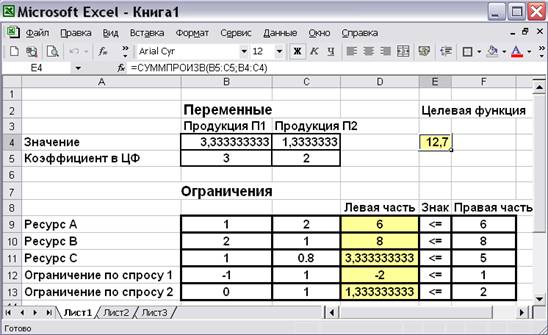
Рис.9.13. Результат применения «Поиска решения»
Если в результате решения задачи выдано окно с сообщением о невозможности нахождения решения (рис.9.14), это означает, что при оформлении задачи была допущена ошибка (не заполнены формулы для ограничений, неправильно установлен «флажок» максимизации/минимизации и т.д.).
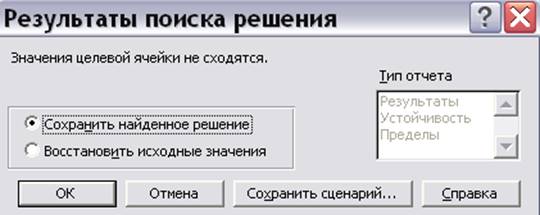
Рис.9.14. Сообщение об ошибке
В данном разделе рассмотрен общий формат решения задач оптимизации в Excel. В зависимости от экономических моделей, выполняют его соответствующие модификации.
Например, можно установить условие на целочисленность некоторых переменных.
9.2. Анализ отчётов по результатам, пределам и устойчивости
Анализ решения задач линейного программирования можно проводить с помощью отчетов, выдаваемых MS Excel в результате решения с помощью надстройки «Поиск решения».
Для получения отчётов в диалоговом окне «Результаты поиска решения» (см. рис. 8.12) в окне «Тип отчёта» следует выбрать соответствующий отчёт «Результаты», «Устойчивость», «Пределы». После нажатия на кнопку «OK» отчёты будут представлены на отдельных листах с соответствующими названиями.
При анализе отчёта по результатам следует обратить внимание на колонку «Статус». Если статус имеет значение «связанное», то это говорит о том, что ресурс, который соответствует ограничению, был использован полностью. Т.е. этот ресурс является дефицитным.
При анализе отчёта по устойчивости следует обратить внимание на следующее.
Нормированная стоимость (часто, редуцированная стоимость, от английского: cost reduction – уменьшение затрат) показывает, насколько по модулю уменьшится целевая функция при принудительном выпуске единицы данной продукции. Т.е., если нормированная стоимость положительна, то увеличение соответствующей переменной приведёт к уменьшению целевой функции. Другими словами, выпуск продукта, соответствующего рассматриваемой переменной, является нерентабельным (неприбыльным).
Допустимое увеличение показывает, насколько максимально можно увеличить коэффициент целевой функции (цену продукта), чтобы структура оптимального плана осталась прежней. Допустимое уменьшение, наоборот, показывает, насколько можно максимально уменьшить коэффициент ЦФ, чтобы осталась прежней структура оптимального плана.
Теневая цена в отчётах Excel показывает, как изменится целевая функция при изменении запаса ресурса на единицу. Понятно, что если ресурс использован полностью, то теневая цена этого ресурса положительна. Допустимое увеличение и уменьшение показывают границы, в которых могут изменяться ресурсы, чтобы структура оптимального решения, т.е. номенклатура выпускаемой продукции, остались без изменений.
В отчёте по устойчивости указаны значения целевой функции при значении переменных на нижнем и верхнем пределах.
Для более подробного самостоятельного изучения возможностей использования MS Excel для анализа рекомендуется следующая литература: Орлова И.В. «Экономико-математические методы и модели. Выполнение расчетов в среде Excel» Практикум. М.: «Финстатинформ»,2000.
9.3. Задачи и упражнения
9.3.1. Решить задачу из п. 1.5.2 и применением MS Excel.
9.3.2. Решить задачу из п. 1.5.2, приведённую к ЗЛП с двумя переменными (см. результаты выполнения упражнения 2.5.2) с применением MS Excel. Сделать выводы по результатам решения этой задачи и задачи из п. 9.3.1.
1. Грызина Н.Ю., Мастяева И.Н., Семенихина О.Н.. Математические методы исследования операций: Учебное пособие / Московский государственный университет экономики, статистики и информатики. М.: МЭСИ, 2003
2. Мастяева И.Н., Горбовцов Г.Я., Семенихина О.Н., Турундаевский В.Б., Математические методы исследования операций./ Учебное пособие. Московский международный институт эконометрики, информатики, финансов и права. - М.: , 2002. Алферова З.В. и др. "Линейная алгебра", М.:МЭСИ, 2000.
3. Строцев А.А. Методы оптимизации систем управления. Часть1. Методы оптимизации линейных задач. Тексты лекций. МО РФ, 1996.
4. Мину М. Математическое программирование. Теория и алгоритмы. – М.: Наука, 1990.
5. Карманов В.Г. Математическое программирование. – М.: Наука, 1986.
6. Сборник задач по высшей математике для экономистов: Учебное пособие. – М.: ИНФРА-М, 2003.
7. Моисеев Н.Н., Иванилов Ю.П., Столярова Е.М. Методы оптимизации. – М.: Наука, 1978.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.