Решение задач по теме ромб

Решение задач

Цели: закрепить в процессе решения задач полученные знания и навыки, подготовить учащихся к контрольной работе.

Ход урока

I. Проверка домашнего задания.

Учащимся гораздо труднее дается применение признаков фигур, чем использование их свойств. Поэтому необходимо не только повторить рассматривавшиеся в определениях, теоремах и задачах признаки параллелограмма, прямоугольника, ромба и квадрата, но и обратить внимание учащихся на различие в применении свойств и признаков.

Устно:

1. Определите вид четырехугольника АВСD, если АС и ВD – диаметры одной окружности.

Ответ: АВСD – параллелограмм, так как его диагонали пересекаются и делятся точкой пересечения пополам. Из равенства диагоналей делаем вывод о том, что он является прямоугольником.

2. Верно ли, что четырехугольник, у которого диагонали взаимно перпендикулярны, является ромбом.

Ответ: нет. Посмотрите на чертеж. Какое еще условие должно выполняться?

3. Дан четырехугольник, у которого два противоположных угла прямые. можно ли утверждать, что такой четырехугольник всегда будет прямоугольником?

Ответ: Нет. Смотрите на рисунок. Какое еще условие должно выполняться?

Вывод:

– Если по условию задачи дано, что четырехугольник является параллелограммом (или прямоугольником, или ромбом, или квадратом), то можно использовать в решении любое его свойство;

– Признаки используются, когда нужно доказать, что данный четырехугольник является параллелограммом (прямоугольником, квадратом или ромбом). При этом нужно привести определенный набор фактов, достаточный для того, чтобы сделать вывод о виде четырехугольника.

4. Всякий ли четырехугольник, у которого есть две параллельные стороны, является трапецией?

Ответ: Нет. Параллелограмм, у которого есть две параллельные стороны, не является трапецией.

5. Является ли данный четырехугольник трапецией?

Ответ: Да, ВС || АD, АВCD.

II. Решение задач.

№№, 438.

№ 438.

Решение

1) 2 =3 как накрест лежащие при ВС || АD и секущей АС.

2) 1 =2 = 3 = 30°,

1 + 2 = 60° АВСD – равнобокая трапеция.

3) АВС – равнобедренный треугольник, так как 1 = 3.

4) СD против угла 30°, поэтому АD = 2СD.

5) По условию АВ + ВС + СD + АD = 20

3СD + 2СD = 20

СD = 4

АD = 2СD = 8 (см).

Задача

1. В ромбе АВСD биссектриса угла ВАС пересекает сторону ВС и диагональ ВD соответственно в точках M и N. Найдите АNВ, если АМС = 120°.

Решение Вариант III

1. ВСО = ВАО.

Пусть ВАN = САМ = х°;

ВСА = 2х°;

АМС: 2х + х + 120° = 180°;

х = 20°.

ВОА: АВО = 90° – 40° = 50°;

ВNА: ВNА = 180° – 50° – 20°;

ВNА = 110°.

III. Самостоятельная работа.

Вариант I

1. Через точку пересечения диагоналей параллелограмма АВСD проведена прямая, пересекающая стороны АD и ВС соответственно в точках Е и F. Найдите стороны параллелограмма, если его периметр равен 28 см. АЕ = 5 см, BF = 3 см.

Ответ: 6 и 8 см.

2. Найдите меньшую боковую сторону прямоугольной трапеции, основания которой равны 10 см и 6 см, а один из углов равен 45°.

Ответ: 4 см.

3. 1. Найдите углы ромба, если его диагонали составляют с его стороной углы, один из которых на 30° меньше другого.

1. АВО на 30° больше ВАО.

АВО – прямоугольный;

ВАО = х°, АВО = х + 30°;

ВАО + АВО = 90°;

х + х + 30 = 90°;

х = 30°.

Вариант II

1. Биссектрисы углов А и D параллелограмма АВСD пересекаются в точке М, лежащей на стороне ВС. Найдите стороны параллелограмма, если его периметр равен 36 см.

Ответ: 6 и 12 см.

2. Найдите боковую сторону равнобедренной трапеции, основания которой равны 12 см и 6 см, а один из углов равен 120°.

Ответ: 6 см.

3. Угол между диагоналями прямоугольника равен 80°. Найдите углы между диагональю прямоугольника и его сторонами.

1. ОС = ОВ DОС – равнобедренный ОСD = СDО = 50°.

Домашнее задание: вопросы 1–20, с. 114–115; готовиться к контрольной работе.

1. В ромбе АВСD D = 140°. Определите углы треугольника АОD (О – точка пересечения диагоналей).

2. На диагонали MP прямоугольника MNPQ отложены равные отрезки МА и РВ. Докажите, что ANBQ – параллелограмм.

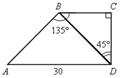
3. Найти ВС.

Решение задач Цели: закрепить в процессе решения задач полученные знания и навыки, подготовить учащихся к контрольной работе

Вывод: – Если по условию задачи дано, что четырехугольник является параллелограммом (или прямоугольником, или ромбом, или квадратом), то можно использовать в решении любое его свойство;…

ВСО = ВАО . Пусть ВАN = САМ = х °;

Угол между диагоналями прямоугольника равен 80°

Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

15.12.2021