Решение задач с параметром 11 класс

Параметры. От простого к сложному

Рассмотрим задачи на параметры различной сложности. В основном это задачи из тренировочных сборников к ЕГЭ. Приводим достаточно подробные решения с объяснением всех шагов. Первые задания попроще.

1. а) При каких значениях a неравенство

                                                       (1)

выполняется при всех x и k?

б) При каких значениях a найдутся такие x и k, при которых неравенство (1) выполняется? [1]

Решение. а) Таких значений a не существует, так как при k = 0 неравенство (1) имеет вид  Оно не выполняется при всех значениях x ни при a = 0 (для любых x), ни при a > 0 (для x < 0), ни при a < 0 (для x > 0).

б) Найдём все значения a, при каждом из которых найдётся решение неравенства

                                                          (2)

Если a = 0, то неравенство (2) справедливо при любом x и при любом k ≠ 0. 

Если a > 0, то неравенство (2) справедливо при любом x > 0 и при любом k.

Если a < 0, то неравенство (2) справедливо при любом x < 0 и при любом k.

Это означает, что при любых значениях a найдутся такие x и k, при которых неравенство (1) выполняется.

Ответ. а) Таких значений a не существует; б) при любых значениях a.

2. При каких значениях величины h многочлен от x

        (1)

является квадратом квадратного трёхчлена относительно x? [1]

Решение. Пусть  — исходный квадратный трёхчлен, тогда его квадрат имеет вид

               (2)

Так как (1) и (2) один и тот же многочлен, то коэффициенты при соответствующих степенях x равны. Тогда справедливы четыре равенства:

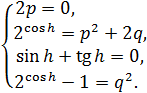                                                                   (3)

Так как p = 0, то q = , а   . Осталось решить систему двух уравнений

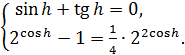                                                           (4)

Из второго уравнения системы (4) получим, что , т. е. что , где  — целое число. Все такие  являются решениями первого уравнения системы (4). Все наши рассуждения строились на явно не высказанном предположении, что система (3) имеет решения, поэтому сделаем проверку. Система (3) имеет решения: , , , где  — целое число.

Ответ. , где  — целое число.

3. Найдите все значения а, для каждого из которых число решений относительно x уравнения

                                                (1)

не превосходит числа решений относительно y уравнения

[1]       (2)

Решение. Уравнение (1) перепишем в виде

                                        (3)

Уравнение (3) квадратное, оно имеет не менее одного корня, так как его дискриминант D равен

Если  ≤ 0, т. е. если  ≤ , то правая часть уравнения (2) не имеет смысла, в этом случае уравнение (2) корней не имеет, а значит, все a, такие, что  ≤  не удовлетворяют условиям задачи.

Это означает, что уравнение (1) имеет единственный корень лишь при  = .

Уравнение (2) при  =  имеет вид

 

                                                                   (4)

Уравнение (4) имеет единственный корень , следовательно,  =  удовлетворяет условиям задачи.

При a ∈  уравнение (1) имеет два корня, а уравнение (2) имеет вид

                                

где A > 0 и B — числа. Это уравнение имеет не более одного корня, так как функция z =  является возрастающей (как сумма возрастающих функций).

Это означает, что любое a, такое, что a ∈  не удовлетворяет условиям задачи.

Ответ.  = .

В следующей задаче нахождения значений параметра B является лишь небольшим эпизодом решения.

4. Найдите наибольшее и наименьшее значения выражения

,

если величины x, y, z,  удовлетворяют системе уравнений

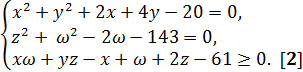                         (1)

Решение. Сначала перепишем систему в виде:

 

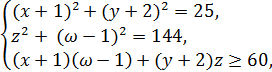
затем в виде:

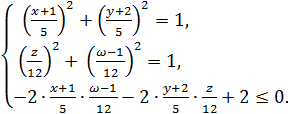                            (2)

Перепишем систему (2), используя новые неизвестные а =,
b = , m = , n = :

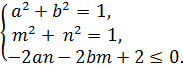                                                 (3)

Подставив вместо числа 2 в неравенство системы (3) выражение , перепишем неравенство системы (3) в виде:

                                             (4)

Из неравенства (4) следует, что, система (3) имеет решения лишь при условии a = n, b = m.

Преобразуем выражение A:

 = = =
= =
.

Таким образом, задача свелась к отысканию наибольшего и наименьшего значений выражения B = , где a и b — числа, удовлетворяющие системе:

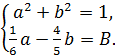                                                               (5)

 Первое уравнение системы (5) — уравнение окружности радиуса 1 в системе координат bOa, второе уравнение при каждом значении параметра B задаёт прямую a = 4,8b + 6B в той же системе координат. Искомые наибольшее и наименьшее значения параметра B получатся из условия, что прямая касается окружности. Здесь ответ можно получить геометрическими средствами.

Условие касания прямой и окружности означают, что система (5) имеет единственное решение. Подставим в первое уравнение системы (5) 4,8b + 6B вместо a и выясним, при каких значениях параметра B полученное квадратное уравнение относительно b

24,04                              (5)

имеет единственный корень. Для этого приравняем нулю дискриминант уравнения (5):

.                           (6)

Решив уравнение (7) получим: , откуда получим наибольшее и наименьшее значения B, удовлетворяющие условиям задачи:  и . Теперь можно найти наибольшее и наименьшее значения искомой величины A:

 и .

 Ответ.  и .

5. Найдите все значения а и b, при которых система уравнений

                  (1)

имеет два решения (; ) и  (; ), удовлетворяющие условию

                     . [2]                                               (2)

Решение. 1) Первое уравнение системы (1) преобразуем к виду:

                                   (3)

Получилось уравнение окружности с центром  и радиусом |b|; b , так как в противном случае вместо окружности получится точка и система не будет иметь двух решений. 

2) Второе уравнение системы (1) преобразуем к виду:

                           (4)

Получилось уравнение окружности с центром  и радиусом 3. Так как координаты точки  удовлетворяют уравнению
y = x + 6, то точка  принадлежит прямой y = x + 6.

3) Условие (2) означает, что ,  ≠  и  + +, т. е. точки A (; ) и B (; ) одинаково удалены от начала координат. Это означает, что эти точки лежат на окружности

                                                    (5)

с центром O (0; 0) и радиусом OA.

Из пунктов 1) – 3) следует, что A (; ) и B (; ) являются точками пересечения трёх окружностей: (3), (4) и (5). Но тогда все три центра окружностей лежат на одной прямой, т. е. точка  лежит на прямой , задаваемой уравнением y = –2x. Подставим координаты точки  в уравнение y = –2x:

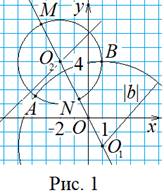a = –2(a – 6),

получим его корень a = 4.

Итак, мы нашли a, осталось найти b.

Окружность (4) задаётся уравнением

Эта окружность пересекает прямую y = –2x в точках M и N, удалённых от точки O на рассто­яние  и  соответственно. Так как  = , то OM =  + 3, ON =  – 3.

Мы получили границы для радиуса |b| окружности (3):

 – 3 < |b| <  + 3.

Ответ. a = 4,   – 3 < |b| <  + 3.

Разберём решение двух задач с модулями. В задаче 7 нет параметров, но работа с ней поможет быстрее освоить решение следующей за ней задачи.

6. Найдите все значения a и n, при которых разность между наибольшим и наименьшим положительными корнями уравнения

равна 18,3. [2]

Решение. Рассмотрим функции вида

 =

и их графики (рис. 2):

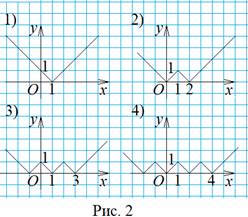1)  = ,

2)  = ,

3)  = ,

4)  = .

Каждый следующий график получается из предыдущего переносом на 1 единицу вниз и отражением отрицательной части графика относительно оси Ox.

Все графики для чётных значений n — 2), 4), … — ведут себя похожим образом. Если прямая y = a пересекает график такой функции более чем в двух точках, то разность d между наибольшим и наименьшим положительными корнями уравнения  = a постоянна и равна n. Эта разность не может быть равной 18,3.

Все графики для нечётных значений n — 1), 3), … — тоже ведут себя похожим образом. Если прямая y = a пересекает график такой функции более чем в двух точках, то разность d между наибольшим и наименьшим положительными корнями уравнения  = a меняется d в пределах

n – 1 ≤ d < n + 1.

Поэтому d = 18,3 лишь при n = 19 (рис. 3). Так как d = AC + CB, то при n = 19 имеем: AB = 18, BC = 0,3. Из равнобедренного прямоуголь­ного треугольника с гипотенузой BC находим a = 0,5BC = 0,15.

Ответ. При n = 19, a = 0,15.

Для самоконтроля решите похожую задачу, заменив 18,3 на 2019. Должен получиться ответ: при n = 2019, a = 0,5.

7. Решите уравнение

|х – 1| + |х + 1| + |х – 2| + |х + 2| + … + |х – 100| + |х + 100| = 200х. [3]

Решение. Обратим внимание на то, что если x ≥ 100, то все модули раскрываются со знаком «+» и уравнение имеет вид:

200х = 200х.

Его корнем является любое число x, такое, что x ≥ 100. Остаётся выяснить, есть ли у исходного уравнения корни левее точки x = 100. На каждом из промежутков, на которые разбивают координатную ось числа 1, –1, 2, –2, … 100, –100, функция

f (x) = |х – 1| + |х + 1| + |х – 2| + |х + 2| + … + |х – 100| + |х + 100|

является линейной, а на всей своей области определения R она является непрерывной. На промежутке [100; +∞) функция f (x) задаётся формулой y = 200x. При движении влево от точки х = 100 на каждом следующем участке угловой коэффициент линейной функции на 2 меньше, чем на предыдущем. Следовательно, левее точки (100; 20000) все точки графика функции y = f (x) лежат выше прямой y = 200x, поэтому графики функций y = f (x) и y = 200x не имеют общих точек для x < 100, исходное уравнение на этом промежутке не имеет корней.

Итак, уравнение имеет бесконечное множество корней — все числа полуинтервала [100; +∞).

Ответ. [100; +∞).

Замечание. Здесь полезно повозиться с графиками функций

y = |х – 1| + |х + 1|,  y = |х – 1| + |х + 1| + |х – 2| + |х + 2|, …,

а также решить уравнения

|х – 1| + |х + 1| = 2х,

|х – 1| + |х + 1| + |х – 2| + |х + 2| = 4х, …

8. Найдите все значения b, при которых система уравнений

            (1)

имеет хотя бы одно решение, где

 + … + . [2]

Решение. Система уравнении (1) равносильна системе

       

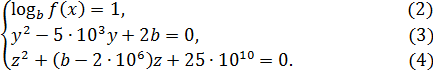
Система уравнений (2), (3), (4) имеет хотя бы одно решение , если выполнены три условия:

1)  b, b > 0, b ≠ 1.

2) ,

3) .

Условия 2) и 3) задают ограничения на b:

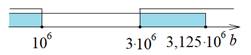 или .

Осталось из условия 1) найти наименьшее значение  функции  . Это число ограничит значения b снизу. Ответ будет иметь вид:

 ≤ b ≤ ,     .

Функция  линейная на каждом из промежутков

(–∞; 0] , , , [; +∞).    

До центрального слагаемого  и после него в сумме по 52 слагаемых:

 + … + .

 Если найти значение функции в любой точке x < , то при раскрытии модулей коэффициент у x будет отрицательный;   если найти значение функции в любой точке x >  , то при раскрытии модулей коэффициент у x будет положительный. Это означает, что слева от точки x =  функция  убывает, справа — возрастает, а в точке
x =  она достигает своего минимума, т. е.  = .

Вычислим  :

  =  + … +  =

=  + … +  +

+  + ) + … + ).

В сумме всего 105 слагаемых. В предпоследней строке, где мы раскрывали модули со знаком «+», получили 53 слагаемых , а в последней строке, где мы раскрывали модули со знаком «–», получили  52 слагаемых . Поэтому все слагаемые, выделенные жирным шрифтом, дадут в сумме  = 2704.

Для вычисления суммы

… ) + … ) =

= 2… ) +

+ … … ) =

= … ) – 2… )

воспользуемся формулой …  = , которая справедлива для любого натурального n и доказывается методом математической индукции.

 = 2704 +  –  = 2704 +  = 286624.

Ответ. 286624 ≤ b ≤ ,   .

9. Найдите наибольшее значение ω, при котором система

             

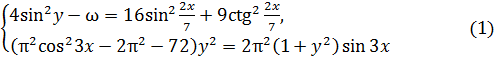
имеет решение. [2]

Решение. Из первого уравнения системы (1) получим, что

                           (2)

Пусть t = , тогда t + 1 =  = , а .

Перепишем равенство (2) в виде:

                             (3)

Так как t ≥ 0, а t + 1 ≥ 1, то в равенстве (3) последнее выражение, заключённое в скобки не меньше 2 (в силу неравенства a + , справедливого для a > 0), причём это выражение равно 2 при условии  = 1, т. е. при условии t = .

Наибольшее значение  получится при условии, что

                                                 (4)

и при этом найдётся значение y, которое вместе с корнем уравнения (4) обращают второе уравнение системы (2) в верное равенство. И то при условии, что увеличить слагаемое  в равенстве (2) невозможно.

Решив уравнение (4), получим, что x = , где n ∈ Z.

Тогда =  = , где n ∈ Z.

Все значения α = , где n ∈ Z, можно задать более простой формулой α = , где k ∈ Z.

1) Если k = 2p, где p ∈ Z, то = 0, α = 1. В этом случае второе уравнение системы (1) имеет вид

,                           

откуда следует, что  = 0 и .

2) Если k = 2p + 1, где p ∈ Z, то возможны два варианта = 1 и = –1.

Если = –1, то α = 0. В этом случае второе уравнение системы (1) имеет вид

,                      

откуда следует, что  = , тогда  и , –14 > –15.

Если = 1, то α = 0. В этом случае второе уравнение системы (1) имеет вид

,                         (5)

но равенство (5) неверно при любом значении , так как левая часть равенства (5) неположительна, а правая часть положительна.

Итак,  при условии, что  = 1. Выясним, можно ли в равенстве (3) увеличить значение выражения .

Из второго уравнения системы (1) выразим :

,

,

.

Разделив обе части полученного равенства на положительное число, получим, что

.

Наибольшее значение дроби достигается при условии, что её числитель достигает наибольшего, а знаменатель наименьшего  значения, что возможно лишь при условии, что  = –1. Это наибольшее значение равно , но тогда

.

Следовательно, увеличить первое слагаемое   в равенстве (3) и тем самым увеличить значение   невозможно.

Ответ. –14.

10. Найдите все значения a, при каждом из которых ровно 5 различных наборов (x; y; z) натуральных чисел x, y, z удовлетворяют системе

                  (1)

Решение. 1) Перепишем первое уравнение системы (1) в виде

                            (2)

Так как x и y — натуральные числа, то каждый множитель в левой части равенства (2) является делителем числа –12. Нетрудно убедиться, что из всех делителей d числа –12 лишь для d = –1, 1, 3 существует натуральный корень уравнения

                                                        (3)

Уравнения

                  

имеют корни  = 1,  = 2,  = 3 соответственно.

Подставив числа , ,  в уравнение (2), получим соответствующие значения y:  = 1,  = 31,  = 29.

Итак, имеется только три пары (x; y) натуральных чисел x и y, удовлетворяющих уравнению системы (1):

 = 1,  = 1;          = 2,  = 31;              = 3,  = 29.   

Рассмотрим неравенство системы (1) для каждой из этих пар.

2) Для  = 1,  = 1 неравенство системы (1) имеет вид:

az + az + a > z,

(1 – 2a)z < a.                                                       (4)

а) Если , то 1 – 2a ≤ 0 и неравенство (4) имеет бесконечно много натуральных решений z, а значит, только для первой пары значений x и y имеется более пяти различных наборов (x; y; z) натуральных чисел x, y, z, удовлетворяющих системе (1).

б) Если , то 1 – 2a > 0 и неравенство (4) равносильно неравенству

z < .                                                             (5)

Если при некотором значении a неравенство (5) имеет натуральное решение , то оно имеет натуральные решения z = 1, 2, …, . Поэтому надо найти такие значения a, при каждом из которых  = 5 — наибольшее натуральное решение неравенства (5). Для этого должно выполняться двойное неравенство

5 <  ≤ 6,

5 – 10a < a ≤ 6 – 12a.                                         (6)

Двойное неравенство (6) равносильно системе

                                                           (7)

Система неравенств (7), а значит, равносильное ей двойное неравенство (6) имеют решения .

Это означает, что для каждого значения a из промежутка  имеется ровно 5 различных наборов (x; y; z) натуральных чисел x, y, z, удовлетворяющих системе (1): (1; 1; 1), (1; 1; 2), (1; 1; 3), (1; 1; 4),
(1; 1; 5).

3) Для  = 2,  = 31 неравенство системы (1) имеет вид:

31az + 2az + 62a > 62z,

(62 – 33a)z < 62a.                                               (8)

а) Если , то 62 – 33a ≤ 0 и неравенство (8) имеет бесконечно много натуральных решений z, а значит, для второй пары значений x и y имеется более пяти различных наборов (x; y; z) натуральных чисел x, y, z, удовлетворяющих системе (1).

б) Если , то 62 – 33a > 0 и неравенство (8) равносильно неравенству

z < .                                                          (9)

Чтобы  = 5 было наибольшим натуральным решением неравенства (9), должно выполняться двойное неравенство

5 <  ≤ 6,

310 – 165a < 62a ≤ 372 – 198a.                          (10)

Двойное неравенство (10) равносильно системе

                                                    (11)

Система неравенств (11), а значит, равносильное ей двойное неравенство (10) имеют решения .

Это означает, что для каждого значения a из промежутка  имеется ровно 5 наборов (x; y; z) натуральных чисел x, y, z удовлетворяющих системе (1): (2; 31; 1), (2; 31; 2), (2; 31; 3), (2; 31; 4), (2; 31; 5).

Отметим, что промежутки значений a, полученные в пунктах 2) и 3), не имеют пересечений, значит, на каждом из них выполнены условия задачи.

4) Для  = 3,  = 29 неравенство системы (1) имеет вид:

29az + 3az + 87a > 87z,

(87 – 32a)z < 87a.                                               (12)

а) Если , то 87 – 32a ≤ 0 и неравенство (12) имеет бесконечно много натуральных решений z, а значит, для третьей пары значений x и y имеется более пяти различных наборов (x; y; z) натуральных чисел x, y, z, удовлетворяющих системе (1).

б) Если , то 87 – 32a > 0 и неравенство (12) равносильно неравенству

z < .                                                          (13)

Чтобы  = 5 было наибольшим натуральным решением неравенства (13), должно выполняться двойное неравенство

5 <  ≤ 6,

435 – 160a < 87a ≤ 522 – 192a.                          (14)

Двойное неравенство (14) равносильно системе

                                                    (15)

Система неравенств (15), а значит, равносильное ей двойное неравенство (14) имеют решения .

Это означает, что для каждого значения a из промежутка  имеется ровно 5 наборов (x; y; z) натуральных чисел x, y, z удовлетворяющих системе (1): (3; 29; 1), (3; 29; 2), (3; 29; 3), (3; 29; 4), (3; 29; 5).

Отметим, что промежутки значений a, полученные в пунктах 2), 3) и 4) не имеют пересечений, значит, на каждом из них выполнены условия задачи. 

Итак, имеется три промежутка значений a, удовлетворяющих условиям задачи: , , .

Ответ. ∪  .

Выражаю сердечную благодарность М. Г. Назарову за помощь в подборе задач для данной заметки, надеюсь получить на адрес электронной почты, указанный в начале, предложения и замечания, улучшающие решения. Более простые и интересные решения тех же задач могут быть добавлены в текст заметки с указанием авторов решений. Пишите.

 

Используемая литература

1. Ткачук В. В. Математика – абитуриенту. 15-е изд., исправленное и дополненное. М.: МЦНМО, 2008. – 1024 с.

2. Козко А. И., Панферов В. С., Сергеев И. Н., Чирский В.Г. ЕГЭ 2011. Математика. Задача С5. Задачи с параметром /Под ред. А. Л. Семенова и И. В. Ященко. – М.: МЦНМО, 2011. – 144 с.

3. Сергеев И. Н. ЕГЭ. Практикум по математике: подготовка к выполнению части С, В. С. Панферов, И. Н. Сергеев. – М.: Издательство «Экзамен», 2012. – 126, [2] с. (Серия «ЕГЭ. Практикум»).

4. Сергеев И. Н. Математика. Задачи с ответами и решениями: пособие для поступающих в вузы. – М.: КДУ: Высшая школа, 2003. – 336 с.