Решение задач теме "Трапеция " с дополнительным построением

236

13

Поучи учителя

1149 подписчиков

Подписаться

Эти 5 дополнительных построений решат любую задачу про трапецию

22 октября 2019

4,1 тыс. дочитывания

1,5 мин.

5,6 тыс. просмотров. Уникальные посетители страницы.

4,1 тыс. дочитываний, 73%. Пользователи, дочитавшие до конца.

1,5 мин. Среднее время дочитывания публикации.

На радость восьмиклассникам расскажем про универсальный набор, который поможет справиться с любой задачей про трапецию. Заодно докажем признаки и свойства равнобедренной трапеции.

Проведите прямую, параллельную стороне

Сайт для аттестующихся педагоговСвидетельство сразу. Всероссийское издание Портал Педагога. Взнос от 90 р.Свидетельство сразу. Всероссийское издание Портал Педагога. Взнос от 90 р.portalpedagoga.ruПубликацииВебинарыКонференцииКонкурсыВсероссийские конкурсыОфициальное СМИСайт для аттестацииПерейти₽

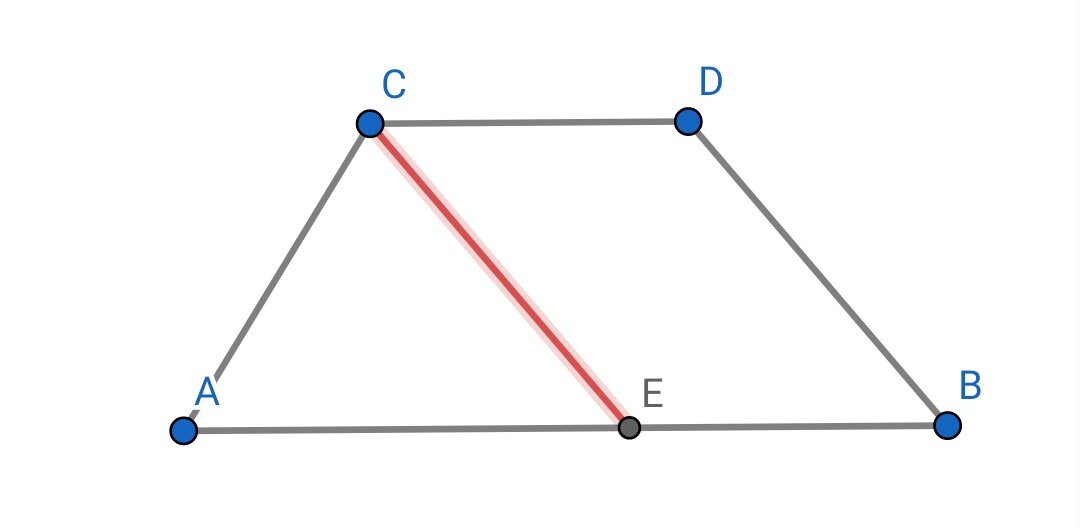
Задача: докажите, что в равнобедренной трапеции углы при основании равны.

Проведем СЕ. СЕВD — параллелограмм. АСЕ — равнобедренный треугольник. Отсюда следует равенство углов.

Это построение пригодится, если в задаче есть разность оснований трапеций, она тут есть — отрезок AE.

Продлите боковые стороны до пересечения

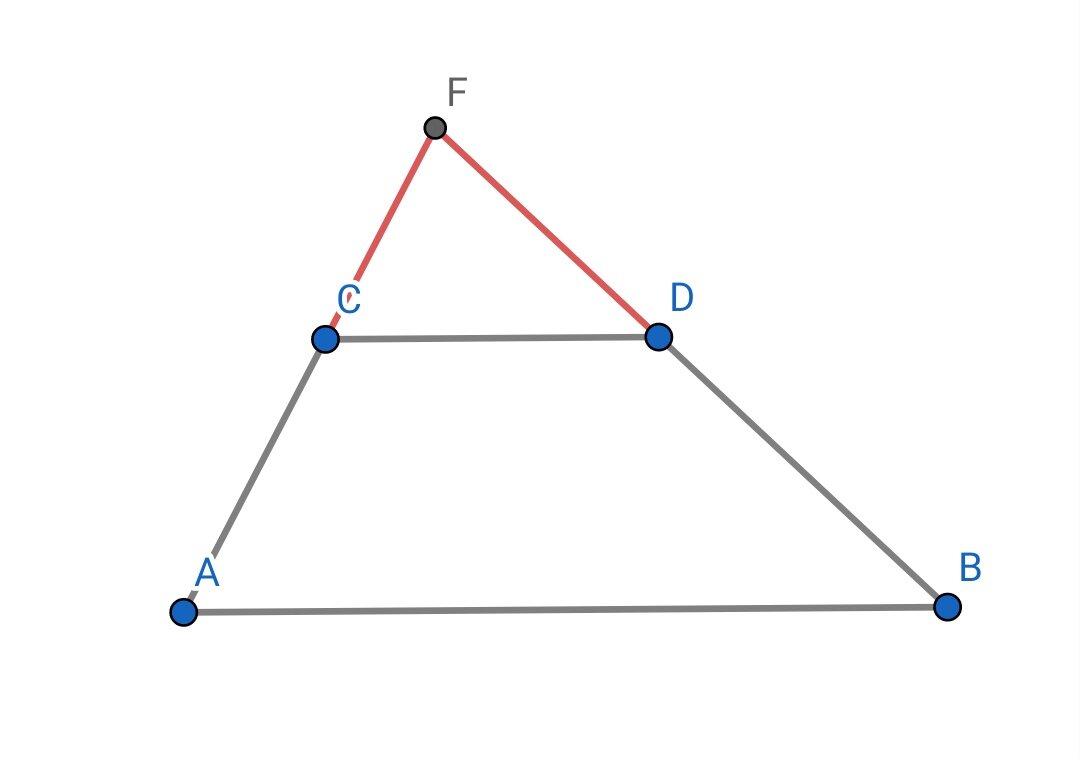
Задача: докажите, что если в трапеции углы при основании равны, то она равнобедренная.

Продлим стороны до пересечения. AFB — равнобедренный треугольник, CFD — тоже. Значит AC=BD

Опустите высоты

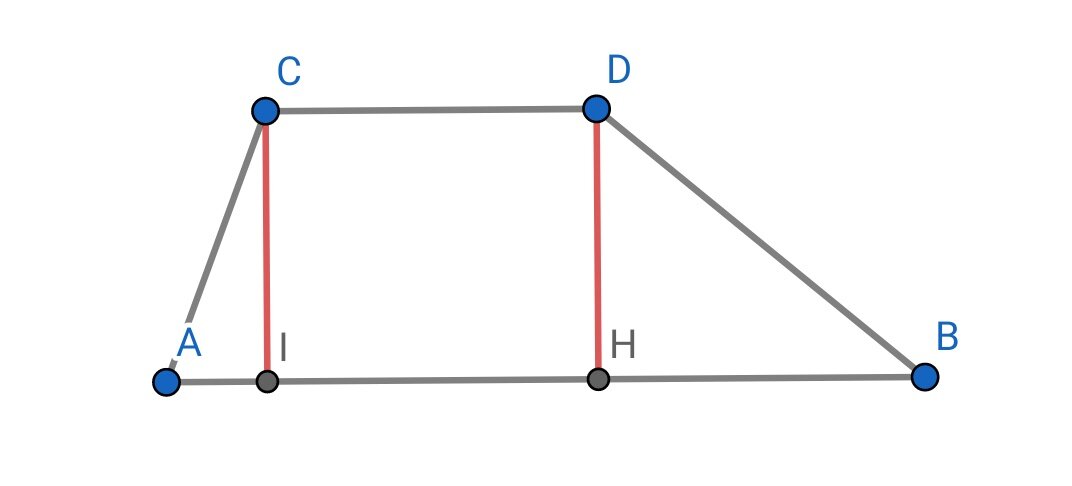
Задача: в равнобедренной трапеции равны диагонали.

Опустим высоты. Треугольники ACI и BDH равны по гипотенузе и острому углу. AI=BH, значит AH=BI. Значит треугольники ADH и CBI равны по двум катетам. Отсюда AD = BC.

Проведите прямую, параллельную диагонали

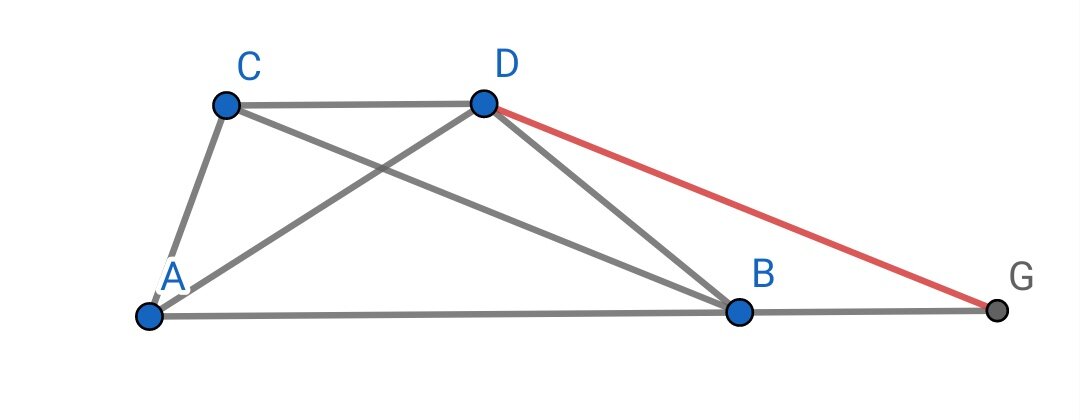
Задача: если в трапеции диагонали равны, то она равнобедренная.

Проведем DG параллельно CB. Из равнобедренности треугольника ADG получим равенство углов ∠DAB=∠DGB=∠DCB=∠ADC. Пусть диагонали пересекаются в точке О. Треугольники ABO и CDO — равнобедренные, значит треугольники ACO и BDO — равные, то есть AC = BD.

Это построение пригодится, если в задаче есть сумма оснований трапеций, она тут есть — отрезок AG.

Проведите прямую через вершину и середину боковой стороны

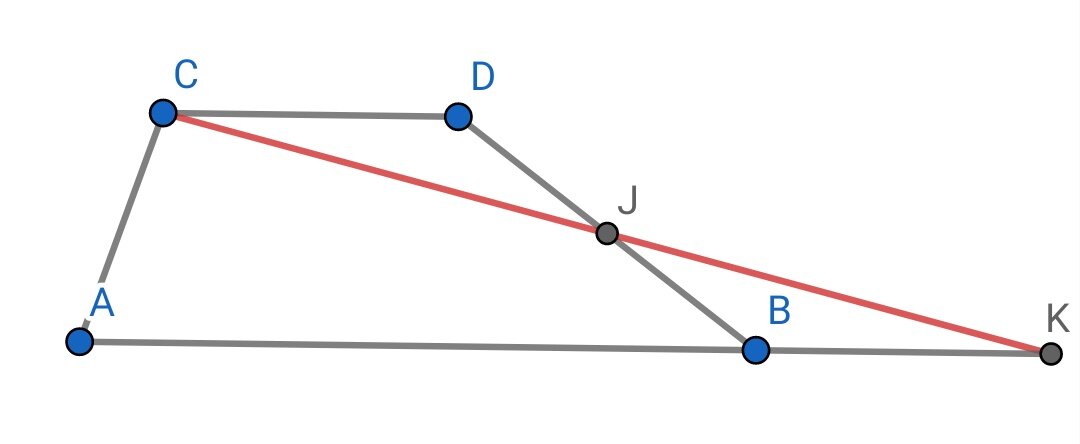
Задача: разрежьте трапецию на две части, из которых можно сложить треугольник.

Решение на чертеже. Треугольники CDJ и BJK равны по стороне и прилежащим к ней углам. Значит, мы разрезали трапецию по отрезку CJ и собрали треугольник ACK.

Комментарий для учителя

Задачи в этой статье собраны не случайно. Сначала решаем с учениками предложенные задачи разными способами. А потом спрашиваем их самих: «ну что, какие мы использовали дополнительные построения для трапеции?».

Пусть школьники сами вспомнят все 5 построений и нарисуют их на доске или плакате. В дальнейшем начинайте решение с вопроса: «Какое построение лучше применить?»

Иллюстрации построены в программе Geogebra, рекомендую.

Вопросы — в комментарии.

Скачано с www.znanio.ru