Реверсия: примеры и контрпримеры, доказательство «от противного», от конца к началу

Реверсия: примеры и контрпримеры, доказательство «от противного», от конца к началу.

Структура занятия.

1.       Мотивационно-ориентировочная часть – 5 мин

2.       Операционно-познавательная часть – 38 мин

3.       Рефлексивно-оценочная часть – 2мин

Ход занятия

Мотивационно-ориентировочная часть

Актуализация

-Посмотрите на рисунки а, б, в и скажите о каких свойствах можно говорить?

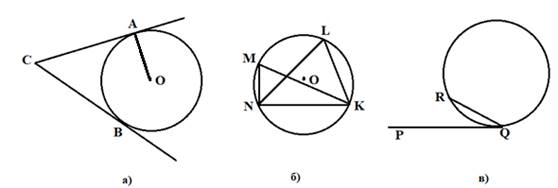
Рисунок 71

(под а) отрезки касательных, проведенных к окружности из одной точки, равны, радиус, проведенный к точке касания перпендикулярен касательной.

б) угол, вписанный в окружность, измеряется половиной угловой величины дуги, на которую он опирается.

вписанные углы, опирающиеся на одну и ту же дугу, равны.

в) угол, образованный касательной и хордой, равен половине дуги, находящейся между его сторонами)

Мотивация

Задача 1. Пусть a, b, c – стороны треугольника, а p – его полупериметр. Доказать, что

-С чего бы вы начали доказывать задачу? (привели ли бы к общему знаменателю выражение в скобках)

-Я предлагаю немного по-другому подойти к данной задаче. Иногда при решении задач полезно задать себе вопрос, насколько правдиво данное высказывание, то есть попробовать подобрать такие значения, при которых можно утверждать, что данное выражение неверно.

Если доказательство утверждения (гипотезу) упирается в громоздкие выкладки, то часто бывает полезно не начинать  с попыток доказательства – нередко предпочтительнее сначала отдать себе отчет, насколько данная гипотеза правдоподобна, не приводит ли она к явно ошибочным или сомнительным выводам, нельзя ли ее опровергнуть.

-Давайте попробуем решить данным способом задачу, т.е. подберем такие числа, при которых выражение будет верно или нет, но перебирать числа мы можем очень долго, какой самый простой случай? (когда a, b и с равны)

- Правильно, проверяем!

()

-Какой вывод сделаем? (утверждение ошибочно)

-Чтобы решить задачу мы с вами подобрали контрпример.

Постановка учебной задачи

Сегодня на занятии продолжаем изучать новые приемы решения геометрических задач, в частности, рассмотрим контрпримеры, доказательство от противного, прием от конца к началу.

Операционно-познавательная часть

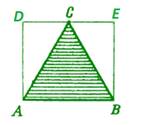
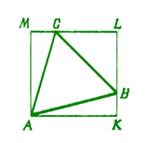
-Начертите прямоугольник, описанный около правильного треугольника (рис. 72 и рис. 73).

-Верно ли суждение о том, что прямоугольник, описанный около правильного треугольника, имеет вдвое больше площадь, чем этот треугольник?

(в 1 случае, да, так как  (AD=BE (т.к. ABED – прямоугольник), AC=BC, DC=CE (т.к. DABC - правильный)) и Þ

-Да, хорошо, для этого случая это верное суждение, но один подтверждающий случай здесь еще ничего не доказывает. Почему?

(Не для всех случаев оно будет верно)

-Правильно, давайте рассмотрим 2 рисунок, который мы с вами начертили. Проведем через точку B прямую BD, параллельную стороне KA, пересекающую сторону AC в точке F (рис. 74). Тогда что мы можем сказать про площади DAFB и DADB?

()

-В свою очередь  как можно выразить через ? (т.к. диагональ прямоугольника AKBD делит его на 2 равных треугольника, то

-То есть получили, что

-Проанализируем теперь . Чему она равна? (проведем высоту CP и тогда )

-А чему равна площадь прямоугольника BDML? ()

-Что мы можем сказать о  и ? (т.к. DB>FB, то )

-Как мы выразим ? (

-Подставим найденные соотношения. Что получим? ()

-То есть мы нашли пример, которые не подтверждает искомое суждение.

-На уроках математики вы сталкивались с методом от противного. Этот метод состоит в том, чтобы взять за основу результат противоположный тому, что нам был задан и от него отталкиваться. Затем, путем рассуждений, приходим к выводу, который противоречит либо условию теоремы, либо какой-либо теореме. На этом основании заключаем, что наше предположение было неверно, а значит, верно утверждение теоремы.

Задача 3. Высота треугольника в два раза меньше его стороны, а один из углов при основании равен 75^o. Докажите, что треугольник равнобедренный.

Дано: DABC

BN=AС

ÐA=75°

Доказать: DABC - равнобедренный

Поиск решения:

-Как можно доказать, что треугольник равнобедренный? (доказать, что боковые стороны равны, или углы при основании равны, или высота является медианой и биссектрисой)

-Я предлагаю вам решить данную задачу следующим образом: предположим, что BC≠AC, тогда какие случаи будем рассматривать? (1 случай - BC<AC, 2 случай – BC>AC)

-Рассмотрим 1 случай, против ÐA=75° лежит сторона BC, а против ÐB лежит сторона AC, что следует из неравенства BC<AC?

(ÐABC >75^o)

-Тогда что можно сказать про градусную меру ÐACB? (ÐACB<30^o)

-Каким является DCBN? И что известное про его катет?

(прямоугольным, катет, противолежащий углу в 30°, равен половине гипотенузы)

-А у нас ÐACB<30^o, тогда какой вывод можно сделать? (BN<BC<AC)

-А это противоречит условию. Самостоятельно докажите, что BC не может быть больше AC.

-Получили, что исходный вариант BC=AC оказался верным.

Решение:

1)      Предположим, что BC≠AC, тогда возможны 2 случая: 1-BC<AC, 2- BC>AC

2)      Рассмотрим 1 случай. Т.к. BC<AC и ÐA=75°, то ÐABC >75^oÞÐACB<30^o

Т.к. DCBN-прямоугольный, то по свойству катета, противолежащего против угла в 30° BN<BC<AC.

3)      2 случай: Т.к. BC>AC и ÐA=75°, то ÐABC <75^o ÞÐACB>30^o

Т.к. DCBN-прямоугольный, то BN>BC>AC. А это противоречит условию

Задача 4. Хорда AB стягивает дугу окружности в 92°. Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.

Дано: AB – хорда

ÈAB=92°

BC - касательная

Найти: ÐABC

Решение:

-Какие дополнительные построения нужно сделать? (Проведем радиусы OB и OA (рис))

-Каким по виду является DAOB? (равнобедренный, т.к. OB=OA=r)

-Откуда можно найти градусную меру ÐABC? (через разность градусных мер углов ÐOBC и ÐOBA)

-Можно ли найти эти углы? (да, по условию задачи ÐAOB=92°Þпо свойству равнобедренного треугольника

ÐOBC=90° по свойству касательной к окружности).

-Сформулируйте свойство касательной к окружности. (Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.)

-И тогда чему равен ÐABC? (46°)

-То есть половине угловой величины дуги AB. Мы получили важное свойство: угол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними.

Данной задачей мы не изучили новый прием, но мы познакомились с новым для вас свойством, которое поможет нам решить следующую задачу.

Задача 5. ABCD – вписанный четырехугольник. Касательные, проведенные в точках B и D, пересекаются в точке M, лежащей на прямой AC. Доказать, что AB·CD=BC·AD.

Дано: ABCD – вписанный четырехугольник

BM, DM – касательные

MÎAC

Доказать: AB·CD=BC·AD

Поиск доказательства: Начнем поиск решения этой задачи с конца, изучая равенство AB·CD=BC·AD, которое нужно доказать.

-К какой равносильной пропорции можно перейти? ()

- Как правило, откуда следуют пропорции? (из подобия треугольников).

- На какие треугольники наша пропорция "указывает"? (на DABD и DBCD)

-Что можно про них сказать? (про их подобие мы ничего сказать не можем, так как они составляют произвольный вписанный четырехугольник).

-Что можно сказать про ∠CBM? (он находится между касательной и хордой и равен  по свойству)

-Какой еще угол равен половине дуги BC? (∠BAC)

-Тогда какие треугольники подобны? (DABM~DBCM, по двум углам: ∠M – общий, а ∠BAC=∠CBM, потому что они измеряются половиной одной и той же дуги BC, как вписанный угол и угол между касательной и хордой)

-А еще какие треугольники будут подобны? (DADM~DDCM по двум углам, т.к. ÐA – общий, ÐAMD=ÐCDM, потому что они измеряются половиной одной и той же дуги CD, как вписанный угол и угол между касательной и хордой)

-Из подобия этих треугольников какие пропорции имеем? (, .)

- Рассмотрим пропорции:  и . Левые части пропорций содержат пропорцию (*).

-Что можно сказать про BM и DM? (BM=DM, как отрезки касательных)

-Какой вывод? (что правые части двух последних пропорций равны, т.е. , а значит )

Доказательство:

1.    AB·CD=BC·ADÞ

2.       DABM~DBCM, по двум углам: ∠M – общий, а ∠BAC=∠CBM, т.к. что они измеряются половиной одной и той же дуги BC, как вписанный угол и угол между касательной и хордойÞ

3.       DADM~DDCM по двум углам, т.к. ÐA – общий, ÐAMD=ÐCDM, т.к. они измеряются половиной одной и той же дуги CD, как вписанный угол и угол между касательной и хордойÞ 

4.     Рассмотрим пропорции:  и .

5.     BM=DM, как отрезки касательныхÞ Þ .

- С чего мы начали решение задачи? (проанализировали равенство, которое нам надо доказать на то, как мы его можем получить)

- В процессе доказательства (решения задачи) рассуждения, как правило, проводят от данного к искомому. Но возможна и схема обратного хода. Для доказательства некоторого утверждения предполагают, что оно верно, и, проводя рассуждения (равносильные преобразования), получают следствие. Ложное следствие означает, что предположение неверно и доказательство заканчивается; истинное следствие означает, что предположение верно, но лишь в том случае, если все рассуждения (преобразования) обратимы.

Рефлексивно-оценочная часть

-Какова была цель занятия? (Отработать решение геометрических задач с использованием поиска в противоположном направлении).

-Достигли ли мы ее? (да)

-Как мы ее достигли? Про какие эвристические приемы вы узнали на сегодняшнем уроке? (контрпримеры, доказательство «от противного», от конца к началу)

Домашнее задание.

1.  Каждая диагональ четырёхугольника разбивает его на два равнобедренных треугольника. Верно ли, что четырёхугольник – ромб ?

2.      Докажите, что если в треугольнике центры вписанной и описанной окружностей совпадают, то этот треугольник равносторонний