Роль геометрических преобразований в решении задач школьного курса по математике

ЧАСТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ-

СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА «НОВЫЙ ПУТЬ»

ИНДИВИДУАЛЬНЫЙ ПРОЕКТ ПО МАТЕМАТИКЕ

ТЕМА:

«Роль геометрических преобразований в решении задач школьного курса математики»

Предмет: математика

Вид проекта:

исследовательский

Выполнил:

Батоян Роберт Левонович,

 учащийся 10 класса ЧОУ-СОШ «Новый путь»

Руководитель:

Санкина Лариса Степановна,

учитель математики

г. Армавир, 2020-2021 учебный год

ОГЛАВЛЕНИЕ

Введение…………………………………………………………...………3-5

ГЛАВА 1.ДВИЖЕНИЯ

1.1Геометрические преобразования ……………...……….………..……6

1.2 Центральная симметрия……………………………………………….6-7

1.2 Симметрия относительно точки………………………......…………..7-8

1.3 Поворот…………………………………….…………...…...………...9-10.

1.4 Параллельный перенос……………………………………..……...…11

1.5 Осевая симметрия……………….…………………………………….11-12

ГЛАВА 2. ПОДОБИЕ

2.1 Подобие………………………………………………...………………13

2.2 Гомотетия……………………………………………………………....13-17

ГЛАВА 3. ЗАДАЧИ С ПРЕОБРАЗОВАНИЯМИ

3.1 Движения………………………………………………………………18-24

3.2  Подобия……………………………………………………….……….24-32

ЗАКЛЮЧЕНИЕ…………………………………………………………….33

СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ………………………….………………………………….34

ВВЕДЕНИЕ

«Раз, стоя перед черной доской и рисуя на ней мелом разные фигуры, я вдруг был поражен мыслью: почему симметрия приятна для глаз? Что такое симметрия? Это врожденное чувство, отвечал я сам себе. На чем же оно основано? Разве во всём в жизни есть симметрия?»

Л. Толстой «Отрочество»

В век всеобщей информатизации человек сталкивается с множеством проблем. Немаловажной среди них является проблема поиска нужной информации за наименьшее время. Ценнейшим умением становится умение обрабатывать материал, включающее в себя систематизацию и выделение главного. Однако, не все люди обладают в должной мере этими умениями, а нехватка литературы, способствующей решению данной проблемы, к сожалению, ощущается в школе.

Настоящая работа обращается к геометрическим преобразованием на плоскости. Большую проблему составляет для данного курса отсутствие задачников. В существующей литературе наблюдается серьезный разрыв между книгами, успешно решающими вопрос пробуждения интереса к миру геометрических преобразований (в них справедливо пропускается теоретический раздел и небольшое место отводится знакомству с симметрией, поворотом, параллельным переносом, гомотетией) и солидными пособиями, со всей строгостью излагающими теоретический материал, и содержащими задачи, способы решения которых не всегда понятны, а указания к решениям носят схематичный характер.

Следовательно, существует потребность в литературе, содержащей как доступный для понимания учащихся, так и подробно изложенный теоретический материал по геометрическим преобразованиям на плоскости, подкрепленный содержательной практической частью - задачами, закрепляющими знания ранее приведенного материала. При этом большинство задач (а особенно содержащие в своем решении ранее не использованные методы) должно быть с подробными пояснениями к решению, понятными замечаниями или, как минимум, ответами. Именно такойматериал станет связующим звеном между первым увлечением удивительным миром преобразований и уже серьезным изучением теории геометрических преобразований, что обосновывает актуальность выбранной темы.

Цель исследования: разработать комплекс практических задач, в основе которых лежит теория геометрических преобразований на плоскости..

Для достижения данной цели определили следующие задачи исследования:

1.        Выполнить анализ и обобщить результаты математической литературы по теории геометрических преобразований на плоскости.

2.        Выстроить логическую цепочку из определений и свойств из теоретического материала теории геометрических преобразований на плоскости.

3.        Разработать комплекс заданий теории геометрических преобразований на плоскости.

4.        Показать решение заданий, включенных в комплекс.

Объектом исследования данной работы является теория геометрических преобразований на плоскости.

Предмет исследования: содержание и решение практических задач в основе которых лежит теория геометрических преобразований на плоскости.

Для решения поставленных задач были использованы следующие методы:

·        анализ математической литературы;

·обобщение  и обработка теоретических положений, включаемых в работу;

·        подбор и решение заданий для комплекса теории геометрических преобразований.

Новизна состоит в следующем:

·        разработан комплекс заданий теории геометрических преобразований;

·        приведены решения заданий, включенных в комплекс.

Практическая значимость состоит в том, что проанализированный и обобщенный теоретический материал, а также разработанный комплекс заданий теории геометрических преобразований на плоскости. может быть использован учителями школы при изучении тем: "Центральная и осевая симметрия. Поворот. Параллельный перенос. Подобие. Гомотетия", в их практической деятельности для повышения качества и эффективности обучения.

Проектная работа состоит из введения, двух глав, заключения и списка литературы.

ГЛАВА 1.ДВИЖЕНИЯ

Геометрические преобразования.

     Преобразования - одно из важнейших понятий математики, возникающее при рассмотрении разного рода соответствий, связывающих элементы различной природы. (9).

    При геометрических исследованиях часто приходится изменять все размеры той или иной фигуры в одном и том же отношении, увеличить радиусы кругов на одну и ту же величину, вообще сопоставлять данной фигуре другую, получаемую из нее по определенным правилам.

    Преобразование называют соответствием, в силу которого каждому элементу Х некоторого множества Х сопоставляется вполне определенный элемент у некоторого другого множества У.

Преобразование - отображение некоторого множества М (наделенного некоторой структурой) в себя. Образ элемента  а Π М при преобразовании и обозначается    u(α) или uα ,  или   α u , или    α^u .

Геометрическое преобразование плоскости - взаимно-однозначное отображение этой  пло   скости на себя. Наиболее важными геометрическими преобразованиями являются движения т.е. преобразования, сохраняющие расстояние. Иначе говоря, если  f-движение пло­скости, то для любых двух точек А, В этой     плоскости   расстояние   между   точками  f(A) и f(B)равно АВ (48).

Преобразование фигур в пространстве определяется таким же образом, как и преобразование фигур на плоскости Помимо преобразования относительно точки и преобразования относительно прямой, в пространстве рассматривают преобразование относительно плоскости.

Движение в пространстве определяется таким же образом, как и на плоскости. При движении в пространстве сохраняются расстояния между точками. И так же, как и на плоскости, прямые переходят в прямые, отрезки в отрезки, углы между полупрямыми сохраняются. Новым свойством, которым обладает движение в пространстве, являются то, что при движении плоскость переходит в плоскость.

Центральная симметрия:

Определения:

Расстоянием между двумя точками будем называть длину отрезка с концами в этих точках.

Преобразованием пространства называется взаимно-однозначное отображение пространства на себя.

при любом преобразовании пространства образы любых двух различных точек пространства различны и любые две различные точки пространства являются образами двух его различных точек.

Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно точки, называется центральной симметрией пространства относительно точки. При этом точка  отображается на себя и называется центром симметрии.

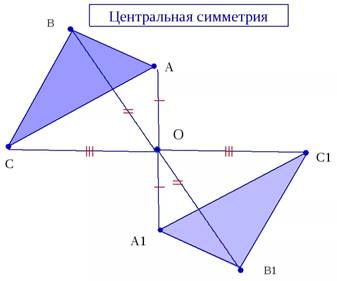
рисунок 1

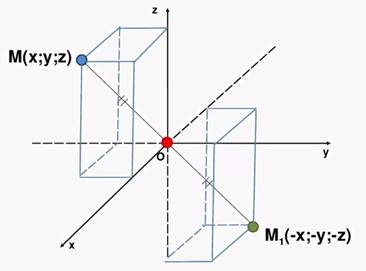
рисунок 2

Симметрия относительно плоскости (зеркальная симметрия):

Определение. Преобразование пространства, при котором сохраняются расстояния между любыми двумя точками, называется движением пространства.

Свойства: при движении в пространстве прямые переходят в прямые, полупрямые – в полупрямые, отрезки – в отрезки, плоскости – в плоскости; сохраняются углы между полупрямыми. Две фигуры называются равными, если они совмещаются движением.

Определение. Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно плоскости , называется симметрией пространства относительно плоскости . Плоскость называется плоскостью симметрии.

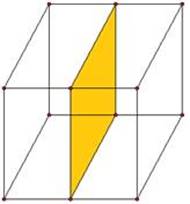
рисунок 3

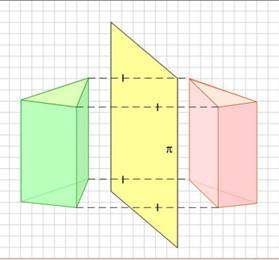
рисунок 4

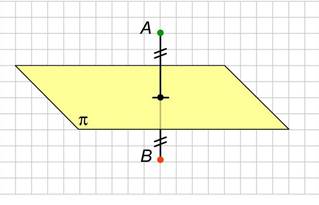
рисунок 5

Поворот:

Определение. Поворотом фигуры вокруг точки  O на угол α в заданном направлении называется такое ее преобразование, при котором каждой точке X фигуры соответствует такая точка X′, что OX′=OX, ∠X′OX=α и луч OX′ откладывается от луча OX в заданном направлении.

Если точка O принадлежит фигуре, то ей соответствует она сама. 

Точка O называется центром поворота, α — углом поворота.

Можно считать, что −180∘<α⩽180∘. При этом число α считается положительным, если направление поворота против часовой стрелки, и отрицательным — если по часовой

Следствия и остальные свойства. 

• Преобразование, обратное повороту, есть поворот с тем же центром на противоположный угол.
• Композиция двух поворотов с общим центром есть поворот на угол, равный сумме углов данных поворотов (возможно, с точностью до прибавления или вычитания 360∘).
• Поворот на нулевой угол является тождественным преобразованием.
• Поворот, отличный от тождественного преобразования, имеет единственную неподвижную точку (центр поворота). Если угол поворота, отличного от тождественного преобразования, не равен 180∘, то неподвижных прямых нет.
• Координатные формулы. Пусть точка M с координатами (x;y) при повороте с центром в начале координат на угол φ переходит в точку M′(x′;y′). Тогда x′=xcos⁡φ−ysin⁡φ и y′=ycos⁡φ+xsin⁡φ.

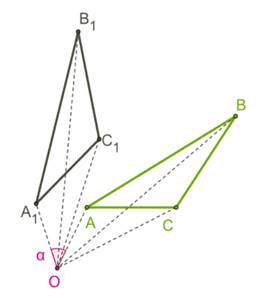
рисунок 6

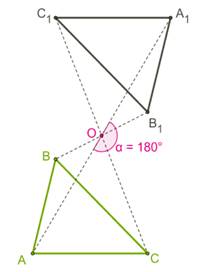
рисунок 7

ц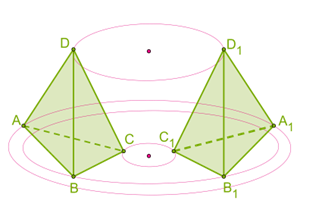

рисунок 8

Параллельный перенос:

Определение. Параллельным переносом на вектор называется такое преобразование пространства, при котором любая точка  отображается на такую точку , что выполняется векторное равенство  . Это перенос (движение) всех точек пространства в одном и том же направлении, на одно и то же расстояние

Если плоскость (прямая) не параллельна вектору переноса, то при переносе на этот вектор она отображается на параллельную ей плоскость (прямуюц).

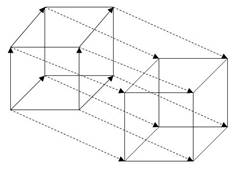
рисунок 9

Осевая симметрия:

Определение. Осевая симметрия — это симметрия относительно проведённой прямой (оси).

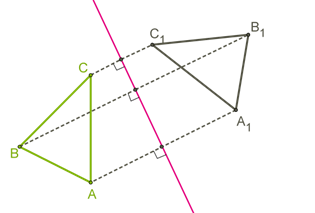
рисунок 10

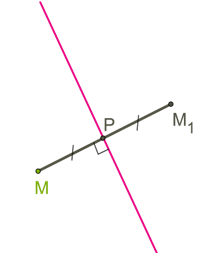
рисунок 11

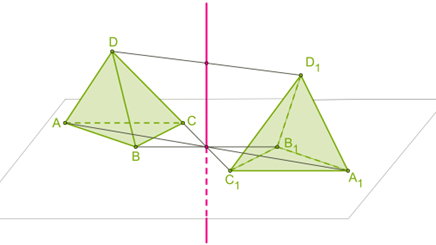
рисунок 12

ГЛАВА 2. ПОДОБИЯ

Подобие:

Подобием называется такое преобразование на множестве точек плоскости, которое изменяет расстояние между произвольными точками плоскости в постоянное число раз  k ( k> 0), то есть, какие бы две точки   M и  N  мы не взяли, в результате преобразования подобия они перейдут в такие точки  M¢ и  N¢ , что   M¢N¢ = k× MN, где через  MN  обозначено расстояние между точками  M и N,  k – коэффициент, число положительное (7).

Каждое движение так же можно рассматривать как преобразование подобия с коэффициентом k = 1.

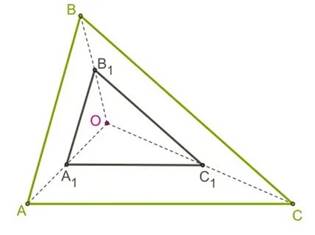
рисунок 13

Гомотетия:

         Ученики 10 класса хорошо знакомы, а ученики 9 класса уже познакомились с такими геометрическими преобразованиями  плоскости как поворот вокруг некоторой точки на заданный угол, параллельный перенос, осевая и центральнаясимметрии. Наша задача: сделать небольшой шаг за рамки школьного учебника и изучить еще несколько замечательных преобразований плоскости. Начнем мы с гомотетии.

         Определение 1. Гомоте­тией с центром О и коэффициентом к¹0 на­зывается геометрическое преобразование, которое произвольно взятую точку А переводит в такую точку А', что ОА' = к×ОА () (рис. 8).

Го­мотетия переводит каждую прямую в парал­лельную ей прямую, каждую окружность сно­ва переводит в окружность. Гомотетия со­храняет углы, а все длины увеличивает в | к | раз: если при гомотетии точки А, В переходят в А'В', то А'В¢= êкê×АВ.Из этого выте­кает, что гомотетия сохраняет форму (но не размеры) фигур; если, например, к > 1, то фи­гура F¢, в которую переходит фигура Fпри гомотетии с центром О и коэффициентом к,представляет собой увеличенную копию фи­гуры F(рис. 1), а если 0<к< 1-уменьшенную копию.

Поскольку при гомотетии все длины изме­няются в одинаковое число раз, отношение длин не меняется. На этом основаны раз­личные способы оценки расстояний; например, зная длину руки и длину большого паль­ца и прикинув, сколько раз большой палец вытянутой руки укладывается в видимом образе предмета, можно найти отношение вы­соты  вертикального предмета к расстоянию до него (на рис. 9) имеем АВ:ВО = А'В¢: В¢ О, откуда, измерив  ВО, можно найти АВ, а потому и высоту трубы, которая примерно втрое больше   АВ(48) .

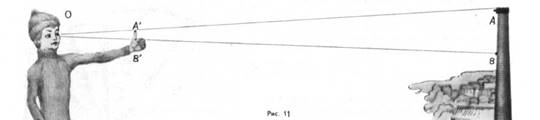
рисунок 15

Фигура  F называется подобной  фигуре  F¢, если существует преобразование подобия, при котором  F  ®  F¢. Подобная фигура является отношением эквивалентности, то есть обладает свойствами: рефлексивности, симметричности и транзитивности.

     Преобразование подобия точки, лежащие на одной прямой, преобразуются в точки , так же лежащие на одной прямой с сохранением порядка их следования. Действительно, соотношение  АВ + ВС = АС выполняется только для трех точек одной прямой, таких, что В лежит между А и С . Но из справедливости этого отношения для А,В,С следует что

A¢B¢ + D¢C¢  = kAB + kBC = k ( AB + BC ) = kAC = AC   ,то есть точки А¢, В¢, С¢, так же лежат на одной прямой и В  находится между А¢С¢

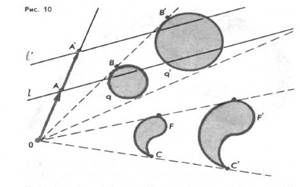
Подобие есть взаимно – однозначное отражение эвклидова пространства –пространство, свойства, которого описываются аксиомами евклидовой геометрии. (20 (Т2); 395) на себя. Подобие сохраняет порядок точек на прямой, то есть, если точка В лежит между точками А и С и В¢, А¢ ,С¢   - соответствующие их образы при некотором подобии, то  В  так же лежит между точками А¢, С¢ точки , не лежащие на прямой, при любом подобии переходят в точки, не лежащие на одной прямой. Подобие преобразует прямую в прямую; отрезок в отрезок; луч в луч; угол в угол; окружность в окружность. Однако, в отличие от гомотетии, подобие может переводить прямую в прямую, не параллельную ей. При подобии угол сохраняет величину (рис. 10).

Простейшие свойства гомотетии:

  1. Гомотетия есть взаимнооднозначное отображение евклидова пространства в себя с одной неподвижной точкой.

 2. При к = 1 гомотетия есть тождественное преобразование.

 3. Гомотетия задается чаще всего (геометрически) центром гомотетии и парой соответственных точек. Гомотетия есть аффинное преобразование – взаимно однозначное точечное отображение плоскости на себя, при котором трем точкам, лежащим на одной прямой соответствуют три точки, так же лежащие на одной прямой (20 (Т1);362)-имеющие одну (и только одну) двойную точку.

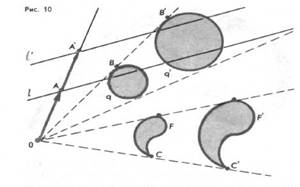
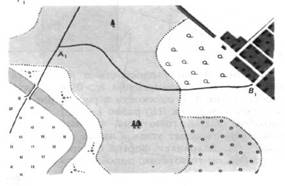
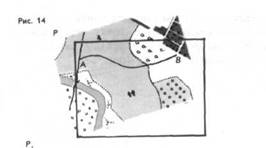На рис. 11 и 12  изображены два плана Р и Р¢,  одного и того же участка местности, выпол­ненные в разных масштабах и по-разному лежащие   на   плоскости.   Эти   планы   представляют собой подобные, но не гомотетичные фигуры;   например,   прямая   АВ   и   соответ­ствующая ей прямая А₁В₁не параллельны. Чтобы получить план Р¢, исходя из плана Р, можно   поступить   так:   сначала   повернуть план   Р,   чтобы   его   стороны   стали   парал­лельными сторонам плана Р¢_; а затем приме­нить гомотетию. Иначе говоря, план Р¢по­добный   Р,   получается   из   Р   при   помощи композиции  движения  (поворота)  и   гомотетии.

Р                     

                                                                                      Р¢

     В элементарной геометрии теория подобия опирается на учение о пропорциональности отрезков. Такой подход был осуществлен еще в «Началах» Евклида, где подобию посвящена 6 книга. Подобие многоугольников определяется следующим образом: два многоугольника подобны, если стороны одного пропорциональны сторонам другого, а углы между пропорциональными сторонами равны.

        Для подобия треугольников необходимым и достаточным является  каждый из следующих признаков:

 1.Стороны одного пропорциональны сторонам другого;

 2. Два угла одного равны двум углам другого;

 3.Две стороны одного пропорциональны двум сторонам другого, а углы между этими сторонами равны;

 4. Две стороны одного пропорциональны двум сторонам другого, а наибольший угол одного равен наибольшему углу другого.

      Два многоугольника подобны тогда и только тогда , если между их точками можно установить взаимнооднозначное соответствие, при котором треугольники с вершинами лежащими в соответствующих точках подобны. Это свойство принимается за определение подобия произвольных фигур. Правильные одноименные многоугольники подобны между собой; подобны так же все окружности. В подобных фигурах углы между каждыми двумя линиями одной фигуры равны углам между соответствующими линиями другой, а отношение расстояния между двумя точками одной фигуры к расстоянию между соответствующими точками другой равно постоянному числу, называемому коэффициентом подобия.

      Площади замкнутых подобных фигур относятся, как квадраты их коэффициентов подобия, а объемы – как кубы.

     Геометрическое преобразование, при котором каждый треугольник переходит в треугольник, подобный ему, называется подобным преобразованием. Подобное  преобразование является частным случаем аффинного преобразования. Две фигуры подобны тогда и только тогда, когда

            Таким образом, мы доказали, что интересующие нас прямые пересекаются на большой окружности в точке С нетрудно видеть, что точка С однозначно определена хордой MN – это точка через которую проходит касательная к большой окружности, параллельная рассматриваемой хорде

ГЛАВА 3. ЗАДАЧИ С ПРЕОБРАЗОВАНИЯМИ

Задачи на центральную симметрию

Задача . В какую точку перейдет точка  при центральной симметрии относительно точки ? Найти координаты получившейся точки .

рисунок 19

Решение

Вариант . Если точка  переходит в некоторую точку , то  – середина . Значит, координаты точки  есть полусумма координат  и :

То есть точка  имеет координаты .

Вариант . 

Получаем: 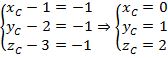. То есть .

Ответ: .

Задача . Докажите, что при центральной симметрии прямая, не проходящая через центр симметрии, перейдет в прямую, параллельную исходной.

Решение

Пусть . Нужно доказать, что  (Рис. 10).

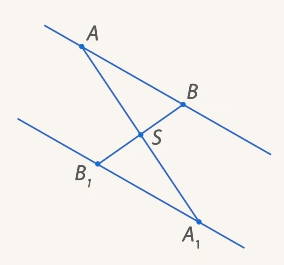
рисунок 20Иллюстрация к условию

Точка  перешла в точку , а точка  – в точку . Образовалась прямая , т.к. образом прямой при движении является прямая.

Распишем вектор :  (коллинеарные векторы). Значит, .

Задачи на осевую симметрию

Задача . Есть ли ось симметрии у прямоугольного параллелепипеда?

(Рис. 21)

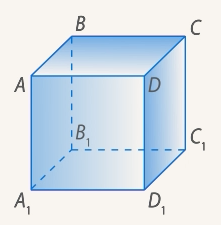
рисунок 21

Решение

Рассмотрим прямую, проходящую через центр любой грани параллелепипеда, перпендикулярно ей (Рис. 19).

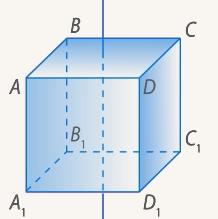
рисунок 22

Рис. 16. Перпендикулярная прямая, проходящая через центр грани

Тогда очевидно, что каждое перпендикулярное сечение будет симметрично относительно этой оси (повернув прямоугольник на , получим такой же прямоугольник), а значит, и вся фигура также будет симметрична.

Ответ: да, есть.

Задача . Рассмотрим правую перчатку. Проведем через средний палец ось параллельно пальцу и сделаем осевую симметрию перчатки относительно этой оси. В какую перчатку: правую или левую перейдет исходная перчатка?

Ответ: В правую перчатку, ведь это просто поворот относительно прямой на .

Задачи на поворот

Задача. Построить отрезок , который получается из отрезка  поворотом вокруг данного центра  на:

а) -150

б) 100

в) 180

Решение.

Для поворота отрезка, повернем концы этого отрезка. Для того, чтобы повернуть точку А, построим прямую ОА. От точки О с помощью транспортира отметим 150° (мы помним, что если угол меньше 0, то поворачиваем по часовой стрелки, то есть угол будем откладывать в эту сторону). С помощью циркуля измеряем расстояние АО и отложим это расстояние на получившейся прямой.

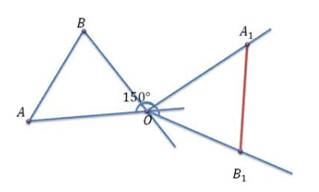
рисунок 23

Поставим точку А₁. Аналогично, построим точку B₁. Тогда получившийся отрезок A₁B₁ – искомый. Для того, чтобы выполнить поворот на 100°, надо 100° отложить против часовой стрелки.

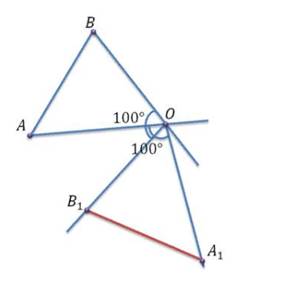
рисунок 24

Все остальные построения проводятся аналогично тому, как мы делали в первом пункте. При повороте на 180° точка A₁ будет лежать на продолжении прямой ОА. Точка B₁ будет лежать на продолжении прямой OB.

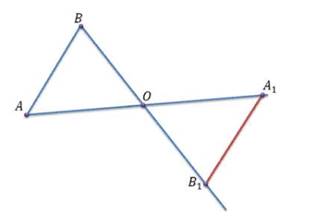
рисунок 25

Задача. Постройте треугольник, который получается из данного треугольника  поворотом вокруг:

а) точки А на 80 градусов

б) вокруг точки О, не лежащей внутри треуольника на 50 градусов

в)  вокруг точки О, лежащей внутри треугольника на -65 градусов

Решение.

Строить треугольник будем по точкам. Поскольку центром поворота является точка А, то она отображается сама на себя. Отобразим точку B. От точки А отложим против часовой стрелки угол равный 80°. Отложим на этой прямой отрезок равный стороне AB и получим точку B₁. Аналогично построим точку C₁. Тогда треугольник AB₁C₁ – искомый.

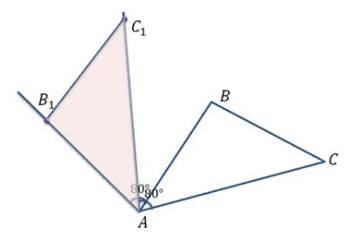
рисунок 26

Проведя аналогичные построения, построим треугольники A₁B₁C₁ для остальных двух случаев.

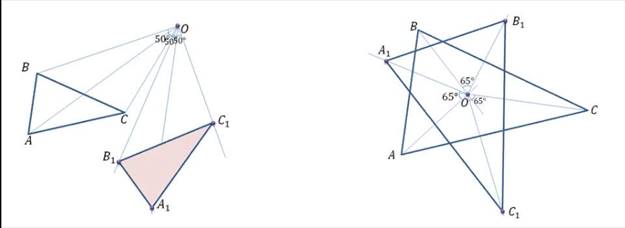
рисунок 27 ; 28

Задачи на параллельный перенос:

Задача: начертить треугольник АВС и вектор а . Построить треугольник А1В1С1, который получится из треугольникa АВС параллельным переносом на вектор а.

Решение: отобразим с помощью параллельного переноса точки А, В, С в точки А1, В1,С1. Соединив полученные точки, мы получим искомый треугольник А1В1С1.

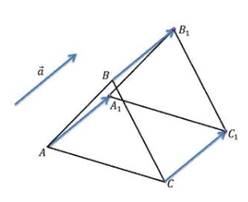
рисунок 28

Задача: начертить пятиугольникABCDE и вектор a. Построить пятиугольник A1B1C1D1E1, который получится из пятиугольника ABCDE параллельным переносом на вектор a.

Решение: 

решать эту задачу будем аналогично тому, как мы решали предыдущую задачу. Отобразим каждую вершину пятиугольника с помощью параллельного переноса на вектор a. Соединим получившиеся точки и получим искомый пятиугольник A1B1C1D1E1.

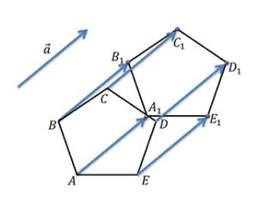
рисунок 29

ЗАДАЧИ  НА ПОДОБИЕ

Для девятого класса:

Проектор полностью освещает экран A высотой 80 см, расположенный на расстоянии 250 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 160 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?

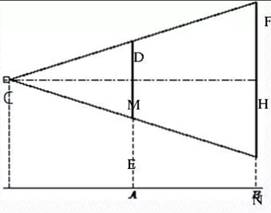
рисунок 30

Решение.

Заметим, что высота экрана, расположенного на расстоянии 250 см, в 2 раза меньше высоты экрана, расположенного на искомом расстоянии, значит, по теореме о средней линии, искомое расстояние в два раза больше первоначального экрана: 250·2 = 500.

Ответ: 500.

Человек ростом 1,7 м стоит на расстоянии 8 шагов от столба, на котором висит фонарь. Тень человека равна четырем шагам. На какой высоте (в метрах) расположен фонарь?

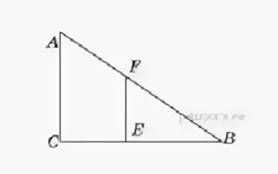
рисунок 31

Решение.

Столб и человек образуют два прямоугольных треугольниках ABC и FEB. Эти треугольники подобны по двум углам. Пусть высота фонаря равна  тогда, поскольку расстояние от фонаря до конца тени равно 12 шагов, получаем:AC:FE=BC:BE

 откуда(1.7*12)/4

Поэтому фонарь расположен на высоте 5,1 м.

Ответ: 5,1.

Короткое плечо шлагбаума имеет длину 1 м, а длинное плечо – 3 м. На какую высоту (в метрах) опустится конец короткого плеча, когда конец длинного плеча поднимается на 1,8 м?

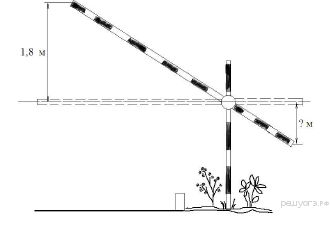
рисунок 32

Решение.

Найдём синус угла, на который поднимается длинное плечо:

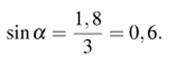
Угол подъема длинного плеча равен углу на который опустится короткое плечо. Пусть x — высота, на которую опустится короткое плечо, имеем:

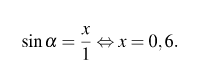
Таким образом, короткое плечо опустится на 0,6 м.

Ответ: 0,6.

Человек ростом 1,8 м стоит на расстоянии 12 м от столба, на котором висит фонарь на высоте 5,4 м. Найдите длину тени человека в метрах.

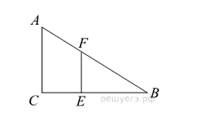
рисунок 33

Решение.

Столб и человек образуют два прямоугольных треугольниках ABC и FEB. Эти треугольники подобны по двум углам. Пусть длина тени равна x, тогда

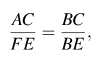
откуда

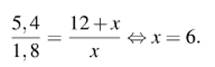
Поэтому длина тени равна 6 м.

Ответ: 6.

На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?

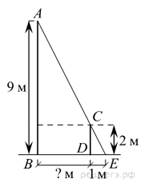
рисунок 34

Решение.

Введём обозначения, как показано на рисунке. Рассмотрим прямоугольные треугольники  и  они имеют общий угол  и, следовательно, подобны по двум углам. Значит,  откуда  Получаем, что 

Ответ: 3,5.

Для одиннадцатого класса:

В треугольнике АВС проведены высоты АК и СМ. На них из точек М и К опущены перпендикуляры МЕ и КН соответственно.

а) Докажите, что прямые ЕН и АС параллельны;

б) Найдите отношение ЕН : АС, если угол АВС равен 30°.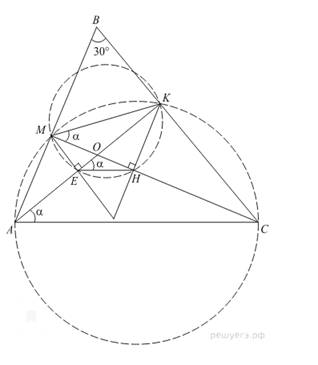

рисунок 35

Решение.

Заметим, что отрезок AC виден из точек K и M под углом 90°, поэтому точки М, К, С и А лежат на одной окружности, диаметром которой является отрезок АС. Аналогично, точки M, K, H, E лежат на окружности, диаметром которой является MK.

Пусть  Тогда , так как они опираются на одну дугу KC в окружности, описанной вокруг четырёхугольника AMKC. Кроме того,  так как они опираются на одну дугу KH в окружности, описанной вокруг четырёхугольника MKHE. Так как  прямые EH и АС параллельны, поскольку это соответственные углы при пересечении EH и AC секущей OA. Это и требовалось доказать.

б) Используем подобие треугольников:

,  кроме того,  поэтому  тогда EH = 

Тем самым искомое отношение длин сторон равно 3:4.

Приведем другое решение пункта б).

Пусть КС = 2x, тогда из треугольника KHC находим HC = X, из ΔOKC: ∠KOC = 30°, тогда OC = 4x, откуда

В силу подобия ΔOEH и ΔОАС получаем:

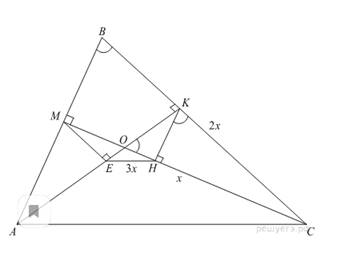
рисунок 36

Приведем решение Александра Шевкина (Москва).

а) Построим вспомогательную окружность с диаметром MK. Она пройдёт через точки E и H, так как 

Построим вспомогательную окружность с диаметром AC. Она пройдёт через точки M и K, т. к. 

По свойству вписанных углов , а , значит, . А это соответственные углы при прямых ЕН и АС и секущей AE. Из равенства этих углов следует параллельность прямых ЕН и АС, что и требовалось доказать.

б) Прямая MK, проходящая через основания высот треугольника ABC, отсекает треугольник KMB, подобный треугольнику ABC. Коэффициент подобия равен 

Рассмотрим треугольники MOK и EOH. Они подобны по двум углам:  (свойство вписанных углов),  (вертикальные). Коэффициент подобия равен 

Умножив полученные равенства

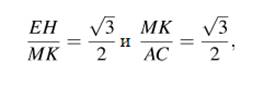
найдём отношение  оно равно 

Ответ: 3:4

Приведем решение Софии Николенко (Москва).

а) Пусть высоты АК и СМ пересекаются в точке О. Рассмотрим треугольник AMO. В нем ME является высотой, проведенной к гипотенузе, поэтому треугольники AME и OME подобны, а углы MAE и OME равны. Пусть эти углы равны α, тогда ∠MOE = 90° − α. Углы KOH и MOE равны 90° − α, тогда угол OKH равен α. Углы EMO и OKH равны так как опираются на одну дугу EH, таким образом, в четырехугольник EMKH можно вписать в окружность.

Четырехугольник AMKC также можно вписать в окружность с диаметром AC. Углы KAC и KMC равны, углы KEH и KMC тоже равны, поэтому угол KEH равен углу KAC. Углы KEH и KAC являются соответственными при пересечении прямых EH и AC секущей AO. Таким образом, прямые EH и AC параллельны.

б) Рассмотрим треугольник AMO, пусть ME = x, тогда

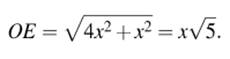
Рассмотрим треугольник AME, в нем: 

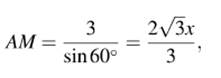
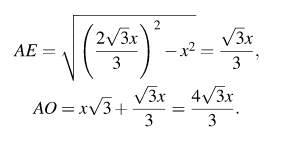
ТреугольникиAOCиEOH подобны по двум углам. Значит, 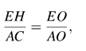 откуда 

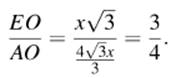
ЗАКЛЮЧЕНИЕ

Геометрические преобразования играют исключительно важную роль в геометрии. Более того, известна трактовка геометрии как науки о свойствах фигур, инвариантных относительно группы геометрических преобразований. Последнюю широко применяют в таких научных областях как физика, химия, биология и т.д.

Применение во внеурочной работе мероприятий на тему «Геометрические преобразования» не только повысит уровень знаний учащихся, но и позволит им освоить способы решений широкого класса задач на доказательство, вычисление, построение и исследование.

В заключении хочется сказать, что использование геометрических преобразований в школьном курсе имеет большое методическое значение. Методы симметрии, поворота, параллельного переноса, гомотетии позволяют учащимся решать большой класс задач. Использование метода геометрических преобразований при решении задач развивает образное мышление, способствует развитию различных форм мыслительной деятельности школьников. Геометрические преобразования являются связующим звеном между курсами алгебры и геометрии. Они используются при построении графиков функций и служат хорошим материалом для развития пространственного воображения, творческих способностей учащихся, воспитания интереса к предмету, самостоятельности, инициативы и других качеств личности.

СПИСОК ЛИТЕРАТУРЫ:

Аммосова Н.В. «Движение фигур на плоскости, их положение и композиция движения» // Математика в школе. – 1987-№3 с.6

Большая советская энциклопедия, М., «БЭС»,1957, т.23,с 413

Большой справочник для школьников. Математика. Изд.дом «Дрофа»   2000.

Вейль Г., Симметрия, пер. с англ., М., 1968.

Вульф Г.В., Симметрия и ее проявление в природе,5 изд., М.-1959.

 Гинзбург А.И., Симметрия на плоскости , Харьков, 1964,

Леонтьев А. Н. Деятельность, сознание, личность. – М., Политизд.,  1975.

Математическая энциклопедия, М., «Советская энциклопедия: 1984.-Т1, Т2, Т4.

Математический энциклопедический словарь - М.: Советская энциклопедия, 1988

Подходова Н.С. Теоретические основы построения курса геометрии 1-6 классов (Целостный подход в обучении геометрии). //Наука и школа.-1999, №1, с 20.

Энциклопедия для детей. Т.11 Математика/ Глав. Ред. М.Д. Аксенова.- М.: Аванта+, 2000.