Самостоятельная работа 11 класс

Вариант 1

1.    Расстояние между пристанями А и В равно 77 км. Из А в В по течению реки отправился плот, а через 1 час вслед за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот проплыл 40 км. Найдите скорость моторной лодки в неподвижной воде, если скорость течения реки равна 4 км/ч. Ответ дайте в км/ч.

2.    Водолазный колокол опускают на дно озера. В начальный период времени в нем находится v = 2 моля воздуха. Во время погружения воздух изотермически сжимается до объема V₂, при этом вода совершает работу 15960 Дж, которая вычисляется по формуле: A=α⋅v⋅T⋅log​₂​​​(V​₁/​​​​V​₂​) где α=13,3Дж/моль · К – постоянная; T = 300K – температура воздуха. Определите объем V₂, который займет воздух после погружения, если начальный объем 

V₁ = 10 литров. Ответ выразите в литрах.

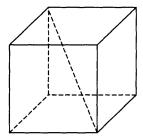
3.    Диагональ куба равна . Найдите его объём.

Вариант 2

1.    Из пункта А в пункт В, расстояние между которыми 60 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 30 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 2 часа 40 минут позже автомобилиста. Ответ дайте в километрах в час.

2.    Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковой сигнал частотой 749 МГц. Приёмник регистрирует частоту сигнала, отражённого от дна океана. Скорость погружения батискафа (в м/с) и частоты связаны соотношением

где = 1500 м/с — скорость звука в воде,f0 — частота испускаемого сигнала (в МГц), f — частота отражённого сигнала (в МГц). Найдите частоту отражённого сигнала, если батискаф погружается со скоростью 2 м/с.

3.    Если каждое ребро куба увеличить на 9, то площадь его поверхности увеличится на 810. Найдите ребро куба.

Вариант 3

1.    В розетку электросети подключены приборы, общее сопротивление которых составляет R1=56 Ом. Параллельно с ними в розетку предполагается подключить электрообогреватель. Определите наименьшее возможное сопротивление R₂ этого электрообогревателя, если известно, что при параллельном соединении двух проводников с сопротивлениями R₁ и R₂ их общее сопротивление задаётся формулой , а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 24 Ом. Ответ дайте в Омах. 

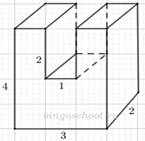
2.    На рисунке изображен многогранник, у которого длины сторон обозначены рядом с соответствующей стороной. Найдите объем данного многогранника, при условии, что все двугранные углы – прямые.

3.    Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 18 км/ч, а вторую половину пути — со скоростью 108 км/ч, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста, если известно, что она больше 63 км/ч. Ответ дайте в км/ч.

Вариант 4

1.    Для определения эффективной температуры звёзд используют закон Стефана — Больцмана, согласно которому мощность излучения нагретого тела PP прямо пропорциональна площади его поверхности S   и четвёртой степени температуры  T:P=σST⁴, где σ=5,7⋅10⁻⁸ - постоянная, площадь измеряется в квадратных метрах, температура — в кельвинах, а мощность — в ваттах. Известно, что некоторая звезда имеет площадь S=1/128​⋅10²⁰м², а излучаемая ею мощность P не менее 1,14⋅10²⁵ Вт. Определите наименьшую возможную температуру этой звезды. Ответ дайте в кельвинах.

2.    На рисунке изображен цилиндр, радиус которого равен 5/π​ , а высота – 4. Определите площадь боковой поверхности цилиндра.

3.    Один гонщик проезжает круговую дистанцию за 12 минут, а второй — за 20 минут. Гонщики стартовали из одной точки этой дистанции, но в разных направлениях.

   Через сколько минут они встретятся?

Вариант 5

1.    Первый куб по объему больше второго в 27 раз. Необходимо определить значение коэффициента, отношения площади поверхности первого куба к площади поверхности второго куба?

2.    Два тела массой m = 2 кг каждое, движутся с одинаковой скоростью v = 10 м/с под углом 2α друг к другу. Энергия (в джоулях), выделяющаяся при их абсолютно неупругом соударении определяется выражением Q = mv2sin2α. Под каким наименьшим углом 2α (в градусах) должны двигаться тела, чтобы в результате соударения выделилось не менее 50 джоулей? Решение. Для решения задачи нам необходимо решить неравенство Q ≥ 50,  на  интервале 2α ∈ (0°; 180°).

3.     

Заказ на 110 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 1 деталь больше?

Вариант 1

1.       18

2.       2,5

3.       64

Вариант 2

1.       15

2.       60

3.       3

Вариант 3

1.       42

2.       20

Вариант 4

1.       4000

2.       40

3.       7,5

Вариант 5

1.       9

2.       751

3.       10

3.75