
ПРИЛОЖЕНИЕ ВЕКТОРНОЙ АЛГЕБРЫ К ДОКАЗАТЕЛЬСТВУ ТЕОРЕМ.
3адача.1. Два
треугольника АВС и ![]() расположены
так, что вершины
расположены
так, что вершины ![]() < последнего
лежат соответственно на лучах
< последнего
лежат соответственно на лучах ![]() кроме того,
кроме того, ![]() . Выяснить, при
каких ограничениях накладываемых на числа
. Выяснить, при
каких ограничениях накладываемых на числа ![]() существует
треугольник
существует
треугольник![]() , стороны которого соответственно
параллельны и конгруэнтны отрезкам
, стороны которого соответственно
параллельны и конгруэнтны отрезкам ![]() .
.
Решение. Из условий задачи следует, что
![]() = λ3c
= λ3c ![]() = λ1a ,
= λ1a , ![]() 2b , где c=
2b , где c= ![]() ,
,
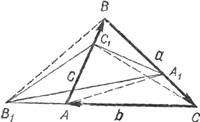
![]() a =
a = ![]() b =
b = ![]() . Отсюда получаем
(см. рис. 1):
. Отсюда получаем
(см. рис. 1):
|
|
|
|
![]() = c + λ1a ,
= c + λ1a , ![]() = a+ λ2b,
= a+ λ2b, ![]() = b+ λ3c
= b+ λ3c
|
|
Треугольник A0B0C0 существует тогда и только тогда, когда выполняется одно из следующих четырех условий:
![]() 1 +
1 + ![]() 1 +
1 + ![]() 1 = 0;
( 1)
1 = 0;
( 1)
![]()
![]() 1 –
1 – ![]() 1 =
0; (2 )
1 =
0; (2 )
![]() 1 —
1 — ![]() 1 +
1 +![]() 1 =
0; ( 3 )
1 =
0; ( 3 )
—![]() 1 +
1 + ![]() 1 +
1 +![]() 1 =
0. ( 4 )
1 =
0. ( 4 )
Подставив значения
векторов ![]() 1 ,
1 , ![]() 1 ,
1 , ![]() 1 из
соотношений (1) в (2) и учитывая, что а + Ь + c = 0, получим: λ1a +
λ2b + λ3c = 0. Так как с = -Ь - а, то отсюда
будем иметь: (λ1 – λ3 )а + (λ2
– λ3 ) Ь = 0.
1 из
соотношений (1) в (2) и учитывая, что а + Ь + c = 0, получим: λ1a +
λ2b + λ3c = 0. Так как с = -Ь - а, то отсюда
будем иметь: (λ1 – λ3 )а + (λ2
– λ3 ) Ь = 0.
В силу неколлинеарности векторов а и Ь получаем: λ1 = λ2 = λ3.
Из соотношения (3), учитывая (1), получаем:
a(1+ λ1 ) + Ь (λ2 — 1) + с (1 — λ3) = 0.
Учитывая, что с = — а — Ь, будем иметь:
а (λ1 + λ3) + Ь (λ2 + λ3 – 2 ) = 0.
Отсюда получаем: λ1 + λ3 = О, λ2 + λ3 — 2 = 0. Так как по условию задачи
λ1 >0 и λ3 > О, то этот случай невозможен. Точно так же убеждаемся в том, что случаи (4) и (5) не могут иметь место. Мы пришли к выводу, что треугольник существует тогда и только тогда, когда λ1 = λ2 = λ3.
В частности, если АА1, ВВ1 и СС1 являются медианами треугольника АВС, то и:
λ1
= λ2 = λ3 = ![]() . и
треугольник А0В0С0 существует.
Мы получили известную теорему элементарной геометрии: для любого
треугольника существует другой треугольник, стороны которого
соответственно параллельны и конгруэнтны медианам исходного треугольника.
. и
треугольник А0В0С0 существует.
Мы получили известную теорему элементарной геометрии: для любого
треугольника существует другой треугольник, стороны которого
соответственно параллельны и конгруэнтны медианам исходного треугольника.
Интересно отметить, что если АА1 ВВ1 и СС1 являются биссектрисами неравностороннего треугольника, то, как легко понять, λ1 , λ2 , λ3. не равны друг другу, и поэтому в данном случае ∆A0B0С0 не существует.
Задача 2. Доказать, что для любого треугольника АВС имеет место соотношение:
BC2 = AB2 + AC2 – 2AB * AC * cos φ ВАС
![]()
![]() где φ = BAC
где φ = BAC
![]()
 Решение.
Введем обозначения:
Решение.
Введем обозначения: ![]() =с,
=с,![]() = Ь
,
= Ь
,![]() = а. Очевидно,
Ь —с = а. Отсюда (b—с)(Ь
— с) = а • а , или
= а. Очевидно,
Ь —с = а. Отсюда (b—с)(Ь
— с) = а • а , или
Ь • Ь — 2bc + сс = аа. Используя
геометрический смысл скалярного произведения, получаем искомый результат.
Следствием этой задачи являются прямая и обратная теоремы Пифагора: для того чтобы треугольник AВС был прямоугольным с прямым углом при вершине А, необходимо и достаточно, чтобы = АВ2 + АС2.
|
|
Задача 3.
Доказать, что для любого треугольника АВС
имеет
место соотношение: /
![]()
где а = ВС, Ь = СА, с = АВ.
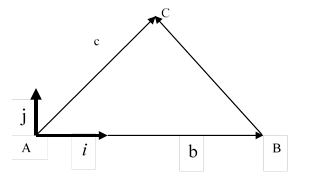
Решение.
Возьмем прямоугольный декартовый базис I, j так, как указано на рисунке 25. Если
обозначить через {α, β} координаты
вектора![]() , то в
силу принятых обозначений будем иметь:
, то в
силу принятых обозначений будем иметь: ![]()
![]() ,
, ![]() {Ь, 0},
{Ь, 0}, ![]() . (
-Ь, 0),
. (
-Ь, 0),
СВ![]() .
.
По формуле известной нам из предыдущего параграфа определим синусы углов
А = ![]()
![]() и C =
и C = ![]() :
:
sin A = ![]() =
= ![]() , sin C =
, sin C = ![]() =
= ![]()
Отсюда,
исключая ![]() ,
получим:
,
получим: ![]() .
Точно так же можно доказать второе соотношение.
.
Точно так же можно доказать второе соотношение.
При решении многих задач весьма полезной является следующая лемма:
Лемма (1) . Если АВС — произвольный треугольник, а М
середина
стороны ВС, то ![]() =
= ![]() (
(![]() +
+ ![]() ).
).
Д о к а з а т е л ь с т в о. Из определения разности векторов имеем:
![]() —
— ![]() =
= ![]() —
— ![]() =
= ![]() . Сложив
эти соотношения в результате получаем: 2
. Сложив
эти соотношения в результате получаем: 2![]() —
— ![]() —
— ![]() = 0,
или
= 0,
или ![]() =
= ![]() (
(![]() +
+ ![]() ).
).
Задача 4. В треугольнике АВС вычислить длину медианы ma , зная угол А и две стороны АВ = с, АС = Ь
Рис 1.
|
|
Решение.
Пусть М — середина стороны ВС треугольника
AВС. Согласно теореме [6,4 ), г)
имеем: ma =![]() ( 1 )
( 1 )
|
|
Согласно лемме (1 ) имеем:
![]() =
=![]() ,
где c =
,
где c =![]() и b =
и b = ![]() .
.
Подставив это значение в ( 1 ) , получаем:b2
ma = ![]()
![]() =
= ![]()
![]() =
= ![]()
![]() .
.
Задача 5. Доказать, что высоты любого треугольника имеют одну общую точку.
Решение. Пусть AВС — данный треугольник, ,0 — точка пересечения
двух высот АН1 и ВН2 (рис. 1 ). Если
обозначить через r1 , r2
и r3 соответственно
векторы ![]() ,
, ![]() и
и ![]() , то
, то ![]() •
• ![]() = 0
и
= 0
и
![]() *
*![]() =
0, поэтому r1 (r3 — r2) = 0
и r2 (r1— r3) =
0.
=
0, поэтому r1 (r3 — r2) = 0
и r2 (r1— r3) =
0.
Воспользуемся следующим тождеством, в справедливости которого легко убедимся, если раскрыть скобки:
( r2 – r1 ) r3 + ( r3 – r2 ) r1 + ( r1 – r3 ) r2 = 0.
Учитывая предыдущие соотношения, получаем:
( r2 – r1 ) r3 =0
или ![]() *
*![]() = 0 .
Отсюда следует, что ОС — высота треугольника АВС.
Задача решена.
= 0 .
Отсюда следует, что ОС — высота треугольника АВС.
Задача решена.
Учитель математики ГКОУ РД «РЦДОДИ» Гаджимирзаев М.М.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.