Сатья на тему: "Сложение векторов"

СЛОЖЕНИЕ ВЕКТОРОВ. СВОЙСТВА.

Операции сложения, вычитание и умножение числа на вектор называется линейными операциями.

Сумма векторов

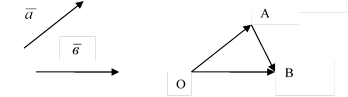
Определение 1.Пусть и - два свободных вектора. Возьмём произвольную точку О и построим вектор =, в затем от точки А отложим вектор =. Вектор , соединяющий начало первого слагаемого вектора с концом второго, называется суммой этих векторов и обозначается +.

Это правило построения суммы двух векторов называется «правилом треугольника».

Определение 2.Суммой векторов  и  с координатами (а_1, а₂) и (в_1, в₂ ) называется вектор с координатами( а₁+в_1, а₂+в₂)_, т.е.

                                (а₁; а₂)+  (в₁; в₂) = (а₁+в₁; а₂+в₂).

Ту же самую сумму векторов можно получить другим способом.

Отложим от точки О вектор = и =. Построим на этих векторах как на сторонах параллелограмм ОАВС. Вектор - служащий диагональю этого параллелограмма, проведенной из точки вершины О, является, очевидно, суммой векторов +. Из рисунка очевидным образом следует, что сумма двух векторов обладает переместительным свойством:

+=+

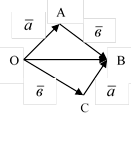
Сумма двух векторов, исходящих из одной точки, выполняется по «правилу параллелограмма».

Пусть, например, даны три вектора , и .

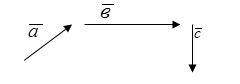
Построим сначала сумму векторов +, а затем, после прибавления к этой сумме , получим некий вектор (+)+. На рисунке =, =, =+, = и =+=(+)+

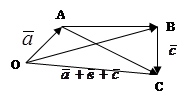
Из рисунка видно, что тот же вектор  мы получим, если к вектору = прибавим вектор =+.Таким образом, (+)+=+(+), т.е. сумма векторов обладает сочетательным свойством. Поэтому сумму трёх векторов , и  записывают просто ++.

Аналогично можно построить сумму четырёх, пяти и вообще любого числа векторов. Это правило построения суммы нескольких векторов называется «правилом многоугольника».

=++++

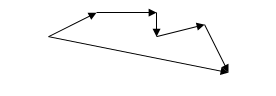
Из произвольной точки О откладывается вектор, равный первому слагаемому вектору. К концу первого вектора присоединяют  начало второго; к концу второго – начало третьего и т.д. Вектор, соединяющий начало первого вектора с концом последнего, является суммой данных векторов.

Если при сложении нескольких векторов конец последнего слагаемого вектора совпадает с началом первого, то сумма векторов равна нулевому вектору. Очевидно, что для любого вектора имеет место следующее равенство +0=.

         Свойства.

Свойства сложения векторов те же, что и свойства сложения чисел.

1^о. Для любых векторов a и b справедливо следующее равенство.

                    a+b=b+a  (1) (коммутативность)

   (переместительный закон, или коммутативность сложения)

Доказательство. (возможны два случая)

       1) Пусть векторы a и b неколлинеарны, отложим от точки А вектор: АВ=a, АД=b-и построим на них параллелограмм АВСД

 АВ+ВС=АС, АД+ДС=АС, АВ=ДС=a, ВС=АД=b имеет место равенство (1).

      2) Пусть векторы a и b коллинеарны. Векторы АВ=а, ВС=b лежать на одной прямой. Так же на этой прямой лежать векторы АВ₁=b и В₁С₁=а. Требуется доказать что точки С и С₁ совпадают. Если а коллинеарен b, то следует из сложения отрезков, а если a неколлинеарен b, то  это следует из вычитания отрезков.

       2^о.  Для любых векторов a,b,c справедливо равенство

                                       (а+b)+c=a+(b+c) (ассоциативность)

             (сочетательный закон, или ассоциативность сложения)

Доказательство.

    От точки А отложим векторы АВ=a, BC=b, CD=c. Тогда (а+b)+c=(AB+BC)+CD=AC+CD=AD, с другой стороны a+(b+c)=AB+(BC+CD)=AB+BD=AD. Отсюда следует (а+в)+с=а+(в+с).

Используя этот закон для трех векторов слагаемое можно группировать любым образом, т.е. скобки можно поставить как угодно. Исходя из этого равенство можно написать никак не объединяя слагаемое скобками.

     Из сочетательного и переместительного законов следует, что сложение векторов как угодно можно переставлять  и группировать слагаемые.

      Векторная ломанная помогает сложить несколько векторов a, b, с, d.

Ломанная состоит из направленных векторов АВ=a, BC=b, CD=c, DE=d.

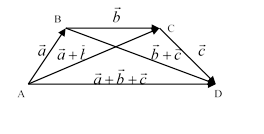                                                              Вектор AE, идущий от начала ломанной   ABCDE и ее конец, AE=a+b+c+d. Если ломанная получилась замкнутой  то сумма векторов равна нуль-вектору.

 3^о. Для любого вектора a имеет место следующее равенство a+0=a.

        Это  очевидное свойства нуль-векторов.(сделать соответствующий рисунок).

   4⁰. Для любого а, существует такой вектор а^!, что: а+ а^!=0- существование обратного вектора.

Разность векторов

Вычитание вектора есть действие обратное сложению.

Разностью векторов   и  называется такой вектор =- , сумма которого с вычитаемым вектором  дает вектор . Таким образом, если =- , то  + =.

Разность векторов  и обозначается так: - .

Из определения суммы двух векторов вытекает правило построения вектора – разности. Откладываем векторы = и = из общей точки О. Вектор , соединяющий концы уменьшаемого вектора  и вычитаемого вектора , является разностью =- . Действительно, по правилу сложения векторов +=, или  + =.

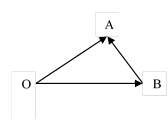
Задачу о построении разности двух векторов можно решить и другим способом.

Пусть даны векторы  и справедливо равенство -=+(-). Разность заменяем сложением.

Вектор - называется противоположным вектору , если вектор  и - имеют равные длины и противоположно направлены.

Для нулевому вектору, противоположным считается сам же нулевой вектор.

Если  - противоположный вектору , то, очевидно, +(-)= 0.

-Противоположный вектор.

Противоположными векторами называется два вектора, если длины равны и они направлены противоположно.

Каждый  из двух векторов называется противоположным другому из них.

0 считается противоположным сам себе.

Вектору a, противоположный –a. Если сложить два противоположных вектора, то в сумме получиться нулевой вектор: a+(-a)=0.

Убедимся в этом. Вектор a=AB изображает перемещение из точки A в точку B. Отложим от точки B вектор –a. Перемещаемся по лучу BA из точки B на расстояние =AB, возвращается в точку A. Итак если a=AB, то –a=BA и

a+(-a)=AB+BA=AA=0.

Верно и обратное утверждение.

Если сумма двух векторов равна нулевому вектору, то они противоположны.

Учитель математики ГКОУ РД «РЦДОДИ»     Гаджимирзаев М.М.