
 .
Абдулино 2018г.
.
Абдулино 2018г.

Содержание
1. Введение
2. Критерии оценивания задач с экономическим содержанием
3. Основные формулы для решения задач
4. Решение «банковских» задач:
- Нахождение количества лет выплаты кредита;
- Вычисление процентной ставки по кредиту;
- Нахождение суммы кредита;
- Нахождение ежегодного транша.
5. Решение задач на оптимизацию
6. Решение одной задачи на оптимизацию различными способами:
- 1 способ – с помощью составления опорной линейной функции;
-2 способ – с помощью логических рассуждений и составления уравнения
- 3 способ – методом перебора.
7. Практикум по решению задач
8. Задачи с ответом
9. Задачи для самостоятельного решения

Текстовая задача с экономическим содержанием – относительно новый вид заданий, появившихся в КИМ ЕГЭ профильного уровня.
Решение таких задач связано со знанием некоторых специфических математических моделей из области экономики, умением переводить сформулированные в виде текста условия в уравнения и неравенства и пониманием того, как решения полученных уравнений и неравенств соотносятся с тем, что написано в условии задачи, – то есть какой смысл имеют полученные результаты.
С чего начать подготовку к решению экономической задачи?
Решение любой текстовой задачи складывается из нескольких основных моментов:
• чтение условия задачи; читайте его до тех пор, покуда сможете, не подглядывая в текст, объяснять суть описанного в задаче процесса (без конкретных числовых данных, конечно, – зазубривать ничего не нужно);
• выбор переменных; для каждого типа задач существуют рекомендации, какие величины лучше всего обозначать как переменные (и это не всегда те величины, о которых идет речь в вопросе задачи); переменных при решении текстовой задачи нужно вводить столько, сколько их нужно для того, чтобы просто и логично составить уравнения и неравенства (не бойтесь, если переменных оказалось слишком много – например, больше, чем число уравнений: если вы все делаете правильно, то «лишние» переменные взаимно уничтожатся или сократятся; еще один вариант – в процессе решения надо будет найти не сами переменные по отдельности, а какую-либо их комбинацию);
• составление уравнений и неравенств, формализация того, что необходимо найти в процессе решения задачи; при составлении уравнений обращайте внимание на единицы измерения – они должны быть одинаковыми для всех одноименных величин;
• решение полученного уравнения, неравенства или системы;
• исследование полученного результата и нахождение ответа на вопрос задачи.


|
Содержание критерия |
Баллы |
|
Обоснованно получен верный ответ. |
3 |
|
Верно построена математическая модель, решение сведено к исследованию этой модели, получен неверный ответ из-за вычислительной ошибки ИЛИ получен верный ответ, но решение недостаточно обосновано. |
2 |
|
Верно построена математическая модель, и решение сведено к исследованию этой модели, при этом решение не завершено. |
1 |
|
Решение не соответствует ни одному из критериев, приведённых выше. |
0 |
|
Максимальный балл |
3 |


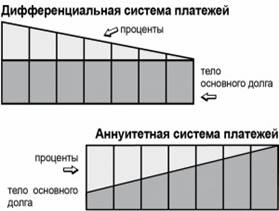
1) Кредиты с равными (аннуитетными) платежами
2) Кредиты с дифференцированными платежами
3) Вклады, сложные проценты
4) Оптимальный выбор
Основные формулы для решения задач:
1) 1% - это 0,01
2) Основные соотношения и выражениями, встречающиеся при решении задач на проценты:
· Число a составляет p% от числа в:
a = ![]() = 0,01bp
= 0,01bp
· Число а увеличили на p%: a·(1+0,01p)
· Число а увеличили сначала на p%, а потом еще на q%:
a·(1+0,01p)·(1+0,01q)
· Число а уменьшили на p%: a·(1 - 0,01p)
3) Задачи, связанные с изменением цены
Пусть So – первоначальная цена, S – новая (окончательная ) цена.
· Повышение цены на a% n раз на a%
S= So ·(1+0,01a) S= So ·(1+0,01a)n
· Понижение цены на a% n раз на a%
S= So ·(1-0,01a) S= So ·(1-0,01a)n
· Удобно пользоваться схематичной записью:
So ·(1+0,01a)
![]()
 a%
a%
Sо d%
So ·(1+0,01a)( 1-0,01d)
 |
Задача №1. Нахождение количества лет выплаты кредита.
Максим хочет взять в банке кредит 1,5 миллиона рублей. Погашение кредита происходит раз в год равными платежами (кроме, может быть, последней) после начисления процентов. Процентная ставка- 10% годовых. На какое минимальное количество лет может Максим взять кредит, чтобы ежегодные выплаты были не более 350 тысяч рублей?
Решение.
1)В конце первого года долг составит: 1500000 ∙ 1,1 – 350000
=1300000 (руб)
2) В конце второго года долг составит: 1300000 ∙ 1,1 – 350000 = 1080000 (руб)
3)В конце третьего года долг составит: 1080000 ∙ 1,1 – 350000 = 838000 (руб)
4)В конце четвертого года долг составит: 838000 ∙ 1,1 – 350000 = 571800 (руб)
5)В конце пятого года долг составит: 571800 ∙ 1,1 – 350000 = 278980 (руб)
6) В конце шестого года долг составит: 278900 ∙ 1,1 =306878 (руб)
Эта сумма менее 350000 руб. Значит, кредит будет погашен за 6 лет. Ответ: 6 лет
Задача №2. Вычисление процентной ставки по кредиту.
31 декабря 2014 года Валерий взял в банке 1000000 рублей в кредит. Схема выплаты кредита следующая. 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга, затем Валерий переводит в банк очередной транш. Валерий выплатил кредит за два транша, то есть за два года. В первый раз Валерий перевел в банк 660000 рублей, во второй раз – 484000 рублей. Под какой процент банк выдал кредит Валерию?
Решение. Пусть а - процентная ставка по кредиту. 1)В конце первого года долг составит:
1000000 ∙ (1 + 0,01∙ а) – 660000 = 340000 + 10000∙а
2) В конце второго года долг составит: (340000 + 10000∙а) ∙ (1 + 0,01∙а) – 484000.
По условию задачи кредит будет погашен за два года. Составляем уравнение: (340000 + 10000∙а) ∙ (1 + 0,01∙а) – 484000 = 0;
![]() + 134∙а – 1440 = 0
+ 134∙а – 1440 = 0
Решая уравнение, получаем, что а = 10. Ответ: 10%
Задача №3 Нахождение суммы кредита.
31 декабря 2014 года Максим взял в банке некоторую сумму денег в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга, затем Михаил переводит в банк 2928200 рублей. Какую сумму взял Михаил в банке, если он выплатил долг четырьмя равными платежами, то есть за 4 года?
Решение. Пусть S – сумма кредита.
1)В конце первого года долг составит: (1,1х – 2928200) рублей
2) В конце второго года долг (в рублях) составит:
(1,1х – 2928200)∙1,1 – 2928200 = 1,21х – 3221020 – 2928200 = 1,21х – 6149220
3) В конце третьего года долг (в рублях) составит:
(1,21х – 6149220)∙1,1 – 2928200 = 1,331х – 6764142 – 2928200 =
=1,331х – 9692342
4) В конце четвертого года долг (в рублях) составит 2928200 рублей: (1,331х – 9692342)∙1,1 = 2928200;
1,4641х – 10661576 = 2928200;
1,4641х = 13589776;
х = 9281999,8.
Значит, сумма кредита равна 9282000 рублей. Ответ: 9282000 руб.
Задача №4. Нахождение ежегодного транша.
31 декабря 2014 года Роман взял в банке 8599000 рублей в кредит под 14% годовых. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга(то есть увеличивает долг на 14%), затем Роман переводит в банк Х рублей.
Какой должна быть сумма Х, чтобы Роман выплатил долг тремя равными платежами (то есть за 3 года)?
Решение.
1)В конце первого года долг составит: 8599000∙1,14 – Х = 9802860 – Х
2) В конце второго года долг составит: (9802860 - Х)∙1,14 – Х=11175260 – 2,14∙Х
3) В конце третьего года долг (в рублях) составит: (11175260 – 2,14∙Х) ∙1,14 – Х=12739796 – 3,4396∙Х. Составим уравнение:
12739796 – 3,4396∙Х= 0
Х=3703860 рублей
Ответ: ежегодный транш составит 3703860 рублей.
Российский математик XIX в. П.Л. Чебышев говорил, что «особенную важность имеют те методы науки, которые позволяют решать задачу, общую для всей практической деятельности человека: как располагать своими средствами для достижениями наибольшей выгоды». С такими задачами в наше время приходится иметь дело представителям самых разных специальностей: инженеры-технологи стараются так организовать производство, чтобы выпускалось как можно больше продукции; конструкторы пытаются разработать прибор для космического корабля так, чтобы масса прибора была наименьшей; экономисты стараются спланировать связи завода с источниками сырья так, чтобы транспортные расходы оказались минимальными, и т. д.
Задачи подобного рода носят общее название — задачи на оптимизацию (от латинского слова optimum — «наилучший»), В самых простых задачах на оптимизацию мы имеем дело с двумя величинами, одна из которых зависит от другой, причем надо найти такое значение второй величины, при котором первая принимает свое наименьшее или наибольшее, (наилучшее в данных условиях) значение.


Задачи на оптимизацию решают по обычной схеме из трех этапов математического моделирования: 1) составление математической модели; 2) работа с моделью; 3) ответ на вопрос задачи. Прежде чем переходить к конкретным примерам решения задач на оптимизацию, дадим некоторые рекомендации методического плана.
Первый этап. Составление математической модели.
1) Проанализировав условия задачи, выделите оптимизируемую величину (сокращенно: О. В.), т. е. величину, о наибольшем или наименьшем значении которой идет речь. Обозначьте ее буквой у (или S, V, R, t — в зависимости от фабулы).
2) Одну из участвующих в задаче неизвестных величин, через которую сравнительно нетрудно выразить О. В., примите за независимую переменную (сокращенно: Н. П.) и обозначьте ее буквой x (или какой-либо иной буквой). Установите реальные границы изменения Н. П. (в соответствии с условиями задачи), т. е. область определения для искомой О. В.
3) Исходя из условий задачи, выразите у через х. Математическая модель задачи представляет собой функцию у = f(х) с областью определения X, которую нашли на втором шаге.
Второй этап. Работа с составленной моделью.
На этом этапе для функции у
= f(х), х ∊ Х найдите ![]() или
или ![]() в зависимости от того, что требуется в условии задачи. При
этом используются теоретические установки, которые мы получили в п. 1 данного
параграфа.
в зависимости от того, что требуется в условии задачи. При
этом используются теоретические установки, которые мы получили в п. 1 данного
параграфа.
Третий этап. Ответ на вопрос задачи.
Здесь следует дать конкретный ответ на вопрос задачи, опираясь на результаты, полученные на этапе работы с моделью.
Задача 1. Прочность балки прямоугольного сечения пропорциональна произведению ее ширины на квадрат высоты. Какое сечение должна иметь балка, вытесанная из цилиндрического бревна радиуса R, чтобы ее прочность была наибольшей?
Решение. Первый этап. Составление математической модели.
 1) Оптимизируемая величина (О. В.) — прочность балки, поскольку
в задаче требуется выяснить, когда прочность балки будет наибольшей. Обозначим
О. В. буквой у.
1) Оптимизируемая величина (О. В.) — прочность балки, поскольку
в задаче требуется выяснить, когда прочность балки будет наибольшей. Обозначим
О. В. буквой у.
2) Прочность
зависит от ширины и высоты прямоугольника, служащего осевым сечением балки.
Объявим независимой переменной (Н. П.) ширину балки, обозначим ее буквой х.
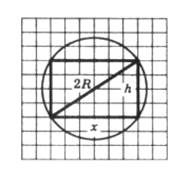
Поскольку осевое сечение представляет собой прямоугольник, вписанный в
окружность радиуса R (рис. 1), то ![]() (при
(при
![]() и
при
и
при ![]() прямоугольник «вырождается» в отрезок,
равный диаметру окружности) — таковы реальные границы изменения независимой
переменной:
прямоугольник «вырождается» в отрезок,
равный диаметру окружности) — таковы реальные границы изменения независимой
переменной: ![]() .
.
3) Высота h прямоугольника
связана с его шириной соотношением ![]() (по
теореме Пифагора). Значит,
(по
теореме Пифагора). Значит, ![]() Прочность
балки у пропорциональна произведению
Прочность
балки у пропорциональна произведению ![]() , т.
е.
, т.
е. ![]()
(где коэффициент k — некоторое положительное число). Значит,
![]() , где
, где ![]()
Математическая модель задачи составлена.
Второй этап. Работа с составленной моделью.
На этом этапе для функции ![]() надо
найти
надо
найти
![]() .Воспользуемся
алгоритмом из п. 1. Имеем:
.Воспользуемся
алгоритмом из п. 1. Имеем:
![]()
![]()
Критических точек нет. Найдем стационарные точки. Приравняв производную нулю, получим
![]()
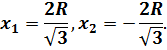
Заданному отрезку ![]() принадлежит лишь
точка
принадлежит лишь
точка ![]()
Осталось вычислить значения функции ![]() в точке
в точке ![]() и
на концах отрезка, т. е. в точках 0 и 2R:
и
на концах отрезка, т. е. в точках 0 и 2R:
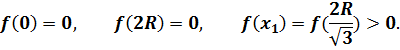
Значит, ![]()
Третий этап. Ответ на вопрос задачи.
В задаче
спрашивается, какое сечение должна иметь балка наибольшей прочности. Мы
выяснили, что ширина х прямоугольника, служащего осевым сечением
наиболее прочной балки, равна ![]() .
Найдем высоту:
.
Найдем высоту:
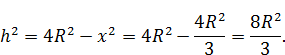
Значит, ![]() , а потому
, а потому ![]()
Ответ. Сечением балки
должен служить прямоугольник, у которого отношение высоты к ширине равно ![]()
Замечание. Квалифицированные мастера приходят к такому же
результату, опираясь на свой опыт, но, разумеется, они принимают указанное
отношение равным 1,4 (приближенное значение иррационального числа ![]() как
раз равно 1,4).
как
раз равно 1,4).
Задача 2. Бак, имеющий вид прямоугольного параллелепипеда с квадратным основанием, должен вмещать V литров жидкости. При какой стороне основания площадь поверхности бака (без крышки) будет наименьшей?
Решение. Первый этап. Составление математической модели.
1) Оптимизируемая величина (О. В.) — площадь поверхности бака, поскольку в задаче требуется выяснить, когда эта площадь будет наименьшей. Обозначим О. В. буквой S.
2) Площадь
поверхности зависит от измерений прямоугольного параллелепипеда. Объявим
независимой переменной (Н. П.) сторону квадрата, служащего основанием бака;
обозначим ее буквой х. Ясно, что![]() .
Других ограничений нет, значит,
.
Других ограничений нет, значит, ![]() .
Таковы реальные границы изменения независимой переменной:
.
Таковы реальные границы изменения независимой переменной: ![]() .
.
3) Если h — высота бака, то ![]() , откуда находим
, откуда находим ![]()
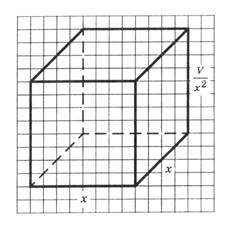
На рис. 2
изображен прямоугольный параллелепипед, казаны его измерения. Поверхность
бака состоит из квадрата со стороной ![]() и
четырех прямоугольников со сторонами
и
четырех прямоугольников со сторонами ![]() и
и
![]() .
Значит,
.
Значит, ![]() .
.
Итак, ![]()
Математическая модель задачи составлена.
 Второй этап.
Работа с составленной моделью. На этом этапе для функции,
Второй этап.
Работа с составленной моделью. На этом этапе для функции, ![]() надо
найти
надо
найти ![]() .
Для этого нужна производная функции:
.
Для этого нужна производная функции: ![]()
![]()
На промежутке (0; +∞) критических точек нет, а стационарная точка только
одна: S’=0 при ![]() .
.
Заметим, что при ![]() выполняется
неравенство
выполняется
неравенство ![]() , а при
, а при ![]() выполняется
неравенство
выполняется
неравенство ![]() . Значит,
. Значит, ![]() —
единственная стационарная точка, причем точка минимума функции на заданном
промежутке, а потому, согласно теореме из п. 1, в этой точке функция достигает
своего наименьшего значения.
—
единственная стационарная точка, причем точка минимума функции на заданном
промежутке, а потому, согласно теореме из п. 1, в этой точке функция достигает
своего наименьшего значения.
Третий этап. Ответ на
вопрос задачи. В задаче спрашивается, какой должна быть сторона основания,
чтобы бак имел наименьшую поверхность. Мы выяснили, что сторона квадрата,
служащего основанием такого бака, равна ![]()
Ответ: ![]()


Задача. В двух шахтах
добывают алюминий и никель. В первой шахте имеется 100 рабочих, каждый из
которых готов трудиться 5 часов в день. При этом один рабочий за час
добывает 1кг алюминия или 3 кг никеля. Во второй шахте имеется 300 рабочих,
каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час
добывает 3 кг алюминия или 1 кг никеля.
Обе шахты поставляют добытый металл на завод, где для нужд
промышленности производится сплав алюминия и никеля, в котором на 2 кг
алюминия приходится 1 кг никеля. При этом шахты договариваются между собой
вести добычу металлов так, чтобы завод мог произвести наибольшее
количество сплава. Сколько килограммов сплава при таких условиях ежедневно
сможет произвести завод?
Решение:
1 способ – с помощью составления опорной линейной функции
Ознакомимся
с решением экстремальных задач по теме «Линейная функция». Решение этих задач
сводится к нахождению экстремума линейной функции у = кх + в, где к
и в – постоянные. Если эту функцию рассматривать на отрезке [![]() ;
; ![]() ], то
она будет иметь на нём наибольшее и наименьшее значение. При к
], то
она будет иметь на нём наибольшее и наименьшее значение. При к![]() 0 наименьшее значение у принимает в точке х =
0 наименьшее значение у принимает в точке х = ![]() , а
наибольшее – в точке х =
, а
наибольшее – в точке х = ![]() , при к
, при к![]() 0 функция у в точке х =
0 функция у в точке х = ![]() принимает
наибольшее значение, а в точке х =
принимает
наибольшее значение, а в точке х = ![]() -
наименьшее. Решим
задачу.
-
наименьшее. Решим
задачу.
А) Пусть х рабочих в 1 шахте добывают алюминий ежедневно, тогда (100-х) рабочих добывают никель. Тогда количество добытого алюминия равно (5х) кг, количество добытого никеля – 15(100-х) кг.
Пусть у рабочих во 2 шахте добывают алюминий ежедневно, (300-у) рабочих добывают никель. Тогда количество добытого алюминия равно (15у) кг, количество добытого никеля – 5(300-у) кг.
Всего количество добытого алюминия: (5х+15у);
количество добытого никеля: 15(100-х)+ 5(300-у)=1500-15х+1500-5у=3000-15х-5у.
Функция сплава: F(x) = (5х+15у) + (3000-15х-5у); F(x) = -10х+10у + 3000;
Учтем условие, при котором производится сплав алюминия и никеля: 2 кг алюминия и 1 кг никеля. Тогда 5х+15у=2(3000-15х-5у). Отсюда у = -1,4х+600. Поставим это выражение в функцию сплава: F(x) = -10х+10(-1,4х+600) + 3000;
F(x) = -24х +5400. Эта линейная функция является убывающей. Наибольшее значение она принимает при х=0. Значит, F(100)=5400.
Ответ:5400
Б) Составим таблицу
|
|
|
Количество рабочих |
Добыча за 1 час |
|
1 шахта |
никель |
х |
3х |
|
|
алюминий |
100-х |
1∙(100-х) |
|
2 шахта |
никель |
у |
1∙у |
|
|
алюминий |
300-у |
3∙(300-у) |
Так как в промышленности для сплава нужно в 2 раза больше алюминия, чем никеля, и на обоих шахтах работают по 5 часов в день, то 5(1∙(100-х)+3∙(300-у))=5(2(3х+1у)). После преобразований получим: у=200-1,4х. Функция выпуска сплава m(х,у)=5(3х+(100-х)+у+3(300-у)). Подставим у, тогда m(х)=3000+24х. Поскольку х≤100, то максимальное значение m(х)=5400 достигается при х=100
Ответ: 5400 кг сплава будет ежедневно выпускать промышленность.
2 способ – с помощью логических рассуждений и составления уравнения
Так как в 1 шахте добывают больше никеля, то для наибольшей выгоды логично допустить, чтобы все рабочие в этой шахте добывали никель. Тогда в 1 шахте будет добыто 1500 кг никеля. Во 2 шахте больше добывают алюминия. Пусть все 300 рабочих добывают алюминий. Тогда алюминия будет добыто 4500 кг. Для сплава нужно алюминия в 2 раза больше, чем никеля. Значит, на 1500 кг никеля нужно 3000 кг алюминия. А у нас алюминия больше. Рассуждаем дальше. Значит, рабочих 2 шахты нужно перераспределить на добычу не только алюминия, но и на добычу никеля с учетом пропорции сплава. Пусть х рабочих 2 шахты добывают алюминий, тогда (300-х) рабочих добывают никель. Составим уравнение:
5 ∙3∙ х =2∙(5∙ (300-х) + 1500);
15х = 6000-10х;
х = 240.
Найдем у: у=300-240=60.Значит, 240 рабочих должны добывать алюминий, 60 рабочих добывать никель. Тогда алюминия будет добыто 240∙ 5∙3 = 3600 (кг), никеля 1500 + 60∙5=1800(кг). Всего 3600+1800=5400 (кг).
Ответ: 5400 кг
3 способ – методом перебора
Так как в 1 шахте добывают больше никеля, то пусть все рабочие добывают никель. Тогда в 1 шахте будет добыто 1500 кг никеля. Во 2 шахте больше добывают алюминия. Пусть все 300 рабочих добывают алюминий. Тогда алюминия будет добыто 4500 кг. Для сплава нужно алюминия в 2 раза больше, чем никеля. Значит, на 1500 кг никеля нужно 3000 кг алюминия. А у нас алюминия больше. Что делать? Значит, рабочих 2 шахты нужно перераспределить на добычу не только алюминия, но и на добычу никеля. Применим метод перебора.
Допустим, что 10 рабочих 2 шахты добывают никель, а 290 рабочих – алюминий. Тогда алюминия будет добыто всего 290∙5∙3= 4350 (кг), а никеля – 1500 + 10∙5= 1550 (кг). Замечаем, что данные не удовлетворяют пропорции 1: 2. Значит, необходимо увеличить количество рабочих, добывающих никель.
Допустим, что 20 рабочих 2 шахты добывают никель, а 280 рабочих – алюминий. Тогда алюминия будет добыто всего 280∙5∙3= 4200 (кг), а никеля – 1500 + 20∙5= 1600 (кг). Замечаем, что данные не удовлетворяют пропорции 1: 2. Значит, необходимо опять увеличить количество рабочих, добывающих никель.
Допустим, что 40 рабочих 2 шахты добывают никель, а 260 рабочих – алюминий. Тогда алюминия будет добыто всего 260∙5∙3= 3900 (кг), а никеля – 1500 + 40∙5= 1700 (кг). Замечаем, что данные не удовлетворяют пропорции 1: 2. Значит, необходимо опять увеличить количество рабочих, добывающих никель.
Допустим, что 60 рабочих 2 шахты добывают никель, а 240 рабочих – алюминий. Тогда алюминия будет добыто всего 240∙5∙3= 3600 (кг), а никеля – 1500 + 60∙5= 1800 (кг). Замечаем, что данные удовлетворяют пропорции 1: 2, то есть на 1 часть никеля приходится 2 части алюминия:
1800: 3600. Итак, всего будет добыто 3600+1800=5400 (кг) алюминия и никеля. А количество изделий из сплава тогда будет равно 1800 штук.
Ответ: 5400 кг
 Задача №17. (Входная
к.р. от 12.09.17, вариант 1)
Задача №17. (Входная
к.р. от 12.09.17, вариант 1)
В бассейн проведены три трубы. Первая труба наливает 30 м3 воды в час. Вторая труба наливает в час на 3V м3 меньше, чем первая (0 < V < 10), а третья труба наливает в час на 10V м3 больше первой. Сначала первая и вторая трубы, работая вместе, наливают 30% бассейна, а затем все три трубы, работая вместе, наливают оставшиеся 0,7 бассейна. При каком значении V бассейн быстрее всего наполнится указанным способом?
Решение.
Пусть
вначале первая и вторая трубы, работая вместе ![]() ч, налили
ч, налили ![]() бассейна, далее все три трубы, работая
вместе
бассейна, далее все три трубы, работая
вместе ![]() ч, налили
ч, налили ![]() бассейна. Тогда время
наполнения бассейна будет равно
бассейна. Тогда время
наполнения бассейна будет равно
![]()
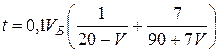 .
.
Необходимо найти наименьшее значение этой функции на интервале (0;10).
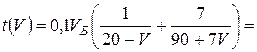
![]()
![]()
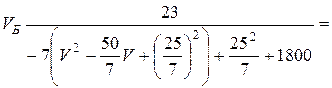
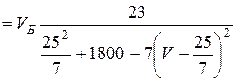 .
.
Отсюда
следует, что функция ![]() будет иметь минимум на интервале (0;10) в
его точке
будет иметь минимум на интервале (0;10) в
его точке ![]() .
.
Ответ: ![]() .
.
1. Задача №17. (Входная к.р. от 12.09.17, вариант 2)
По бизнес-плану предполагается изначально вложить в четырёхлетний проект 10 млн. рублей. По итогам каждого года планируется прирост вложенных средств на 15% по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: по целому числу n млн. рублей в первый и второй годы, а также по целому числу m млн. рублей в третий и четвёртый годы.
Найдите наименьшие значения n и m, при которых первоначальные вложения за два года как минимум удвоятся, а за четыре года как минимум утроятся.
Решение.
К
началу 2-го года будет ![]() млн. руб. вложений, а к началу 3-го года:
млн. руб. вложений, а к началу 3-го года:
![]() .
.
По
условию ![]() .
Наименьшее целое решение
.
Наименьшее целое решение ![]() . Тогда к началу 3-го года будем иметь
. Тогда к началу 3-го года будем иметь
![]() млн. руб.
млн. руб.
К началу 4-года имеем ![]() млн. руб., а в конце проекта:
млн. руб., а в конце проекта:
![]() .
.
По условию ![]() Получаем, что
Получаем, что ![]() ‑ наименьшее целое решение.
‑ наименьшее целое решение.
Ответ: 4 и 1 млн. руб.
2. Задача №17. (Входная к.р. от 12.09.17, вариант 3)
Некто в 2016 году взял в банке кредит в 6,6 млн. рублей под процент, который начисляется один раз в год в середине года. В 2017, 2018 и 2019 году, в начале года, он вносил равные суммы так, что после начисления процента на оставшуюся сумму в июле, долг на конец года был равен 6,6 млн. рублей. Затем, в 2020 и 2021 году, остаток долга выплачивался равными суммами так, что кредит был закрыт в 2021 году. Каков был процент по кредиту, если за весь период кредитования было выплачено 12,6 млн. рублей?
Решение.
Допустим, банк начисляет a процентов, то есть умножает остаток долга на ![]() . Обозначим это
выражение за x. Тогда первые три платежа составляли
. Обозначим это
выражение за x. Тогда первые три платежа составляли ![]() миллионов рублей.
миллионов рублей.
Пусть
четвертый и пятый платежи составляли N миллионов рублей. Тогда ![]() , откуда
, откуда 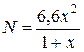 .
.
По
условию 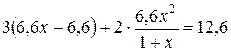 . Решим
это уравнение:
. Решим
это уравнение:
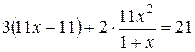
![]()
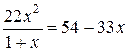
![]()
![]()
![]()
![]()
![]() .
.
Из
смысла задачи следует, что следует исключить отрицательный корень. Таким
образом, ![]() . Тогда
банк начислял 20% годовых.
. Тогда
банк начислял 20% годовых.
Ответ: 20%.
3. Задача №17. (Кр. от 26.10.17, вариант 1)
Вклад в размере 10 млн. рублей планируется открыть на четыре года. В конце каждого года вклад увеличивается на 10% по сравнению с его размером в начале года, а, кроме этого, в начале третьего года и четвёртого годов вклад ежегодно пополняется на одну и ту же фиксированную сумму, равную целому числу миллионов рублей. Найдите наименьший возможный размер такой суммы, при котором через четыре года вклад станет не меньше 30 млн. рублей.
Решение.
В
конце первого года вклад составит 11 млн. рублей, а в конце второго ‑
12,1 млн. рублей. Пусть искомая сумма равна x (млн. рублей).
Тогда в начале третьего года вклад составит ![]() а в конце ‑
а в конце ‑
![]() В начале
четвёртого года вклад составит
В начале
четвёртого года вклад составит ![]() а в конце ‑
а в конце ‑
![]()
По условию, нужно найти наименьшее целое x, для которого выполнено неравенство
![]()
Наименьшее целое решение этого неравенства ‑ число 7. Значит, искомая сумма — 7 млн. рублей.
Ответ: 7 млн. рублей.
4. Задача №17. (Кр. от 26.10.17, вариант 2)
Два велосипедиста равномерно движутся по взаимно перпендикулярным дорогам по направлению к перекрестку этих дорог. Один из них движется со скоростью 40 км/ч и находится на расстоянии 5 км от перекрестка, второй движется со скоростью 30 км/ч и находится на расстоянии 3 км от перекрестка. Через сколько минут расстояние между велосипедистами станет наименьшим? Каково будет это наименьшее расстояние.
Решение.
Обозначим
буквой t время, прошедшее с начального момента времени. Поскольку каждый
велосипедист движется по взаимно перпендикулярным дорогам, то расстояние между
ними может быть вычислено по теореме Пифагора. Рассмотрим ![]() ‑ квадрат длины в
каждый момент времени, тогда:
‑ квадрат длины в
каждый момент времени, тогда:
![]()
![]() .
.
Таким
образом, ![]() ,
, ![]() . У данной квадратичной функции
есть наименьшее значение, которое достигается при
. У данной квадратичной функции
есть наименьшее значение, которое достигается при
![]() (ч)
(ч)![]() (мин).
(мин).
Тогда:
![]() .
.
Отсюда следует, что минимальное расстояние
между велосипедистами равно ![]() (км), и будет достигнуто через 6,96 мин.
(км), и будет достигнуто через 6,96 мин.
Ответ: 6,96 мин, 0,6 км.
5. Задача №17. (Кр. от 26.10.17, вариант 3)
Алексей приобрёл ценную бумагу за 7 тыс. рублей. Цена бумаги каждый год возрастает на 2 тыс. рублей. В любой момент Алексей может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 10%. В течение какого года после покупки Алексей должен продать ценную бумагу, чтобы через тридцать лет после покупки этой бумаги сумма на банковском счёте была наибольшей?
Решение.
Если
Алексей продаст бумагу в течение k-го года, то через тридцать лет после
покупки сумма на его счёте будет равна ![]() Таким образом,
нам нужно найти номер максимального члена последовательности
Таким образом,
нам нужно найти номер максимального члена последовательности ![]() , где k пробегает
целые значения от 1 до 30. Рассмотрим приращение
, где k пробегает
целые значения от 1 до 30. Рассмотрим приращение
![]()
Отсюда
![]() при
при ![]() и
и ![]() при
при ![]() Следовательно,
наибольшее значение последовательность
Следовательно,
наибольшее значение последовательность ![]() принимает при
принимает при ![]() Продать бумагу
следует в течение восьмого года.
Продать бумагу
следует в течение восьмого года.
Ответ: в течение восьмого года.
6. Пример. Митя, Антон и Борис учредили компанию с уставным капиталом 200 000 рублей. Митя внес 14% уставного капитала, Антон – 42 000 рублей, Гоша – 0,12 уставного капитала, а оставшуюся часть капитала внес Борис. Учредители договорились делить ежегодную прибыль пропорционально внесенному в уставной капитал вкладу. Какая сумма от прибыли 1 000 000 рублей причитается Борису? Ответ дайте в рублях.
Решение:
Митя внес 14% или 0,14 уставного капитала. Гоша внес 0,12 уставного капитала.
Антон внес ![]() , а Борис внес 1 – 0,21 – 0,14 – 0,12 =
0,53 уставного капитала. Из прибыли размером в 1 000 000 рублей Борис
получит
, а Борис внес 1 – 0,21 – 0,14 – 0,12 =
0,53 уставного капитала. Из прибыли размером в 1 000 000 рублей Борис
получит ![]() рублей.
рублей.
Ответ: 530 000 рублей.
7. Пример. За некоторый период времени у господина Иванова количество акций увеличилось на 15%. На сколько процентов увеличилась общая стоимость акций господина Иванова, если цена каждой акции увеличилась на 20%?
Решение. Пусть S0 – цена одной акции, n – количество акций, S0· n – общая стоимость акций. Эти величины связаны формулой S = S0· n.
Составим таблицу:
|
|
Цена одной акции |
Количество акций |
Общая стоимость |
|
Было |
S0 |
n |
S0· n |
|
Стало |
1,2S0 |
1,15n |
1,38S0· n |
Можно сразу сделать вывод: общая стоимость акций S увеличилась в 1,38 раз, поэтому стоимость акций увеличилась на 38%.
Или, используя формулу процентного «прироста», находим искомую величину:
![]() ·100 = 38(%).
·100 = 38(%).
Ответ: 38%.
8. Пример. В двух областях есть по 50 рабочих, каждый из которых готов трудиться по 10 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,2 кг алюминия или 0,1 кг никеля. Во второй области для добычи х кг алюминия в день требуется х2 человеко-часов труда, а для добычи у кг никеля в день требуется у2 человеко-часов труда. Обе области поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на1 кг алюминия приходится 2 кг никеля. При этом области договариваются между собой вести добычу металла так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?
Решение: В первой области
50 рабочих отработают 500 часов в сутки. Пусть z человек выпускают
алюминий. Количество металла выпущенное в первой области z ∙ 0,2 +
(500 – z) ∙ 0,1 кг.
А во второй области так же 500 человеко-часов и по условию задачи
х2 + у2 = 500, т.е. х2 = 100, у2 =
400;
х = 10, у = 20.
10 кг алюминия и 20 кг никеля добывают во второй области.
Так как никеля выпускают в 2 раза больше,
то 2(0,2z + 10) = 50 – 0,1z + 20,
0,4z + 20 = 70 - 0,1z,
0,5z = 50,
z = 100.
S(z) = 0,2z + 50 – 0,1z + 30.
S(100) = 0,2
∙ 100 + 50 – 0,1 ∙ 100 + 30 = 20 + 50 – 10 + 30 = 70 + 20 = 90.
Ответ: 90 кг сплава сможет произвести завод за сутки.
9. Пример. В январе 2014 года ставка по депозитам в банке «ВТБ» составляла
х % годовых, тогда как в январе 2015 года — y % годовых, причем известно, что x+y=30%. В январе 2014 года вкладчик открыл счет в банке «ВТБ», положив на него некоторую сумму. В январе 2015 года, по прошествии года с того момента, вкладчик снял со счета пятую часть этой суммы. Укажите значение x при котором сумма на счету вкладчика в январе 2016 года станет максимально возможной.
Решение: Пусть 1-первоначальный вклад. Тогда через год при х % годовых на счету окажется сумма 1∙(1+0,01х). Далее вкладчик снимает со счета пятую часть первоначальной суммы. То есть на счету оказывается сумма 1+0,01х-0,2=0,8+0,01х. В банке меняется процентная ставка и составляет теперь у %, т.е (30-х)%. Тогда еще через год у вкладчика на счету окажется сумма (0,8+0,01х)(1,3-0,01х). Нас интересует значение х, при котором значение f(x) =(0,8+0,01х)(1,3-0,01х) будет максимальным. Исследуем данную функцию методами математического анализа или максимальное значение функция f(x) примет в точке х0 (вершина параболы), то есть в точке х0 =25.
Ответ: 25%.
10.
Пример. Максим хочет взять кредит 1,5 млн.
руб. Погашение кредита происходит раз в год равными суммами (кроме, может быть,
последней) после начисления процентов. Ставка процента 10% годовых.
На какое минимальное количество лет может взять Максим кредит, чтобы ежегодные
выплаты были не более 350 т.р.?
Решение: Представим решение данной задачи в виде таблицы.
|
|
Выплаты Максима |
Начисление банка |
Остаток на конец года |
|
31.12.15 |
|
|
1 500 000 |
|
31.12.16 |
350 000 |
1500000*10%=150 000 |
1500000+150000 - 350000 = 1 300 000 |
|
31.12.17 |
350 000 |
1300000*10% =130 000 |
1300000+130000 – 350000 = 1 080 000 |
|
31.12.18 |
350 000 |
1080000*10% =108 000 |
1080000+108000 – 350000 = 838 000 |
|
31.12.19 |
350 000 |
838000*10% = 83 800 |
838000+83800 – 350000 = 571 800 |
|
31.12.20 |
350 000 |
571800*10% = 57 180 |
571800+57180 – 350000 = 278 980 |
|
31.12.21 |
306 878 |
278980*10% =27 898 |
278980+27898 –306878 = 0 |
Ответ: Максим может взять кредит на 6 лет.
11. Пример. 31 декабря 2014 года Максим взял в банке некоторую сумму денег в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга, затем Михаил переводит в банк 2928200 рублей. Какую сумму взял Михаил в банке, если он выплатил долг четырьмя равными платежами, то есть за 4 года?
Решение. Пусть S – сумма кредита.
1)В конце первого года долг составит: (1,1х – 2928200) рублей
2) В конце второго года долг (в рублях) составит: (1,1х – 2928200)∙1,1 – 2928200 = 1,21х – 3221020 – 2928200 = 1,21х – 6149220
3) В конце третьего года долг (в рублях) составит: (1,21х – 6149220)∙1,1 – 2928200 = 1,331х – 6764142 – 2928200 = =1,331х – 9692342
4) В конце четвертого года долг (в рублях) составит 2928200 рублей: (1,331х – 9692342)∙1,1 = 2928200; 1,4641х – 10661576 = 2928200; 1,4641х = 13589776; х = 9281999,8
Значит, сумма кредита равна 9282000 рублей.
Ответ: 9282000 руб
12. Пример. 31 декабря 2014 года Роман взял в банке 8599000 рублей в кредит под 14% годовых. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга(то есть увеличивает долг на 14%), затем Роман переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Роман выплатил долг тремя равными платежами (то есть за 3 года)?
Решение.
1)В конце первого года долг составит: 8599000∙1,14 – Х = 9802860 – Х
2) В конце второго года долг составит: (9802860 - Х)∙1,14 – Х=11175260 – 2,14∙Х
3) В конце третьего года долг (в рублях) составит: (11175260 – 2,14∙Х) ∙1,14 – Х=12739796 – 3,4396∙Х.
Составим уравнение: 12739796 – 3,4396∙Х= 0
Х=3703860 рублей
Ответ: ежегодный транш составит 3703860 рублей
 |
1. Первичная информация разделяется по серверам №1и №2 и обрабатывается на них. С сервера №1 при объеме t2 Гб входящей в него информации выходит 20t Гб , а сервера №2 при объеме t2 Гб входящей в него информации выходит 21t Гб обработанной информации.
25≤![]() ≤55. Каков наибольший объем
выходящей информации при общем объеме входящей информации в 3364 Гб?
≤55. Каков наибольший объем
выходящей информации при общем объеме входящей информации в 3364 Гб?
Ответ: 1682 Гб.
2. Стоимость изготовления n банок пропорциональна величине 24+4n+n2
При каком количестве банок стоимость изготовления одной банки минимальна?
Ответ: 5 банок.
3. В двух шахтах добывают алюминий и никель. В первой шахте имеется 100 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 1кг алюминия или 3 кг никеля. Во второй шахте имеется 300 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 3 кг алюминия или 1 кг никеля. Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1 кг никеля. При этом шахты договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?
Ответ: 5 400 кг сплава сможет произвести завод ежедневно.
4. Предприниматель купил здание и собирается открыть в нем отель. В отеле могут быть стандартные номера площадью 27 квадратных метров и номера «люкс» площадью 45 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 981 квадратный метр. Предприниматель может поделить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 2000 рублей в сутки, а номер «люкс» 4000 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своем отеле предприниматель?
Ответ: 86 000 рублей сможет заработать в сутки на своем отеле предприниматель.
5. В двух областях есть по 90 рабочих, каждый из которых готов трудиться по 5 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,3 кг алюминия или 0,1 кг никеля. Во второй области для добычи х кг алюминия в день требуется х2 человеко-часов, а для добычи у кг никеля в день требуется у2 человеко-часов труда. Для нужд промышленности можно использовать или алюминий, или никель, причем 1 кг алюминия можно заменить 1 кг никеля. Какую наибольшую массу металлов можно добыть в двух областях суммарно для нужд промышленности?
Ответ: 165 кг металлов можно добыть в двух областях.
6. У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно выращивать картофель и свеклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 300 ц/га, а на втором – 200ц/га. Урожайность свеклы на первом поле составляет - 200 ц/га, а на втором – 300 ц/га. Фермер может продавать картофель по цене 10 000 руб. за центнер, а свеклу - по цене 13 000 руб. за центнер. Какой наибольший доход может получить фермер?
Ответ: 69 000 000 рублей может получить фермер.
7. В двух областях есть по 250 рабочих, каждый из которых готов трудиться по 5 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,2 кг алюминия или 0,1 кг никеля. Во второй области для добычи х кг алюминия в день требуется х2 человеко-часов, а для добычи у кг никеля в день требуется у2 человеко-часов труда. Для нужд промышленности можно использовать или алюминий, или никель, причем 1 кг алюминия можно заменить 1 кг никеля. Какую наибольшую массу металлов можно добыть в двух областях суммарно для нужд промышленности.
Ответ: 300 кг металлов можно добыть в двух областях.
8. У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно выращивать картофель и свеклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 400 ц/га, а на втором – 300ц/га. Урожайность свеклы на первом поле составляет - 300 ц/га, а на втором – 400 ц/га. Фермер может продавать картофель по цене 5 000 руб. за центнер, а свеклу - по цене 6 000 руб. за центнер. Какой наибольший доход может получить фермер?
Ответ: 44 000 рублей может получить фермер.
9. В двух областях есть по 100 рабочих, каждый из которых готов трудиться по 10 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,3 кг алюминия или 0,1 кг никеля. Во второй области для добычи х кг алюминия в день требуется х2 человеко-часов, а для добычи у кг никеля в день требуется у2 человеко-часов труда. Обе области поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1 кг никеля. При этом области договариваются между собой вести добычу металла так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?
Ответ: 240 кг металлов можно добыть в двух областях.
10. На каждом из двух комбинатов работает по 1 800 человек. На первом комбинате один рабочий изготавливает за смену 1 детали А или 2 деталь В. На втором комбинате для изготовления t деталей (и А, и В) требуется t2 человеко-смен. Оба эти комбината поставляют детали на комбинат, из которых собирают изделие, для изготовления которого нужна 1 деталь А и 1 детали В. При этом комбинаты договариваются между собой изготавливать детали так, чтобы можно было собрать наибольшее количество изделий. Сколько изделий при таких условиях сможет собрать комбинат за смену?
Ответ: 1860 изделий
11. На каждом из двух комбинатов работает по 200 человек. На первом комбинате один рабочий изготавливает за смену 1 детали А или 3 деталь В. На втором комбинате для изготовления t деталей (и А, и В) требуется t2 человеко-смен. Оба эти комбината поставляют детали на комбинат, из которых собирают изделие, для изготовления которого нужны 1 деталь А и 1 деталь В. При этом комбинаты договариваются между собой изготавливать детали так, чтобы можно было собрать наибольшее количество изделий. Сколько изделий при таких условиях сможет собрать комбинат за смену?
Ответ: 220 изделий.
12. На каждом из двух комбинатов изготавливают детали А и В. На первом комбинате работает 40 человек, и один рабочий изготавливает за смену 15 детали А или 5 деталей В. На втором комбинате работает 160 человек, и один рабочий изготавливает за смену 5 деталей А и 15 деталей В. Оба эти комбината поставляют детали на комбинат, из которых собирают изделие, для изготовления которого нужны 2 детали А и 1 деталь В. При этом комбинаты договариваются между собой изготавливать детали так, чтобы можно было собрать наибольшее количество изделий. Сколько изделий при таких условиях сможет собрать комбинат за смену?
Ответ: 1800 изделий.
13. Предприниматель купил здание и собирается открыть в нем отель. В отеле могут быть стандартные номера площадью 27 квадратных метров и номера «люкс» площадью 45 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 855 квадратный метр. Предприниматель может поделить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 2000 рублей в сутки, а номер «люкс» - 3000 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своем отеле предприниматель?
Ответ: 63 000 рублей.

1. В городе N живёт 600 000 жителей. Среди них 15% детей и подростков. Среди взрослых 45% не работает (пенсионеры, домохозяйки, безработные). Сколько взрослых работает?
2. Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 8 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
3. Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась втрое, общий доход семьи вырос бы на 112%. Если бы стипендия дочери уменьшилась вдвое, общий доход семьи сократился бы на 3%. Сколько процентов от общего дохода семьи составляет зарплата жены?
4. Фонды оплаты труда четырёх отделов компании соотносятся друг с другом как 2:5:6:3. Определите величину фондов оплаты труда каждого отдела, если суммарный фонд оплаты труда компании равен 64 млн рублей.
5. В целях стимулирования продаж магазин установил 5%-ную скидку на каждую пятую продаваемую посудомоечную машину и 15%-ную на каждую двенадцатую продаваемую посудомоечную машину. В случае если на одну посудомоечную машину выпадают обе скидки, то применяется большая из них. Всего в ходе рекламной акции было продано 500 посудомоечных машин. Определите выручку магазина от продажи партии посудомоечных машин, если цена одной посудомоечной машины составляет 12000 рублей.
6. В январе стоимость проезда в автобусе составила 18 рублей, а в феврале — 20 рублей. На сколько процентов (с точностью до десятых долей процента) повысилась стоимость проезда в феврале?
7. Антикварный магазин, купив два предмета за 450 тысяч рублей, продал их, получив 40% прибыли. Какую цену заплатил магазин за каждый предмет, если на первом прибыли было получено 25%, а на втором 50%?
8. Банк выплачивает своим вкладчикам 6% годовых и даёт ссуды заёмщикам под 15% годовых. Чему равна банковская прибыль за год, если банк привлёк 20 млн рублей средств вкладчиков на год и выдал заёмщикам ссуд в 5 млн рублей на год?
9. Объем промышленной продукции увеличился в 5 раз. На сколько процентов произошло увеличение?
10. После перехода на новое оборудование затраты электроэнергии снизились на 16%, а выпуск изделий вырос на 50%. На сколько процентов уменьшилось количество электроэнергии, расходуемое на производство одного изделия?
11. Цветной телевизор два месяца назад стоил на 20% дешевле, чем месяц назад, когда он стоил на 10% дешевле, чем сейчас. На сколько процентов дешевле стоил телевизор два месяца назад, чем сейчас?
12. Какую сумму положили в банк под простые проценты по ставке 27% годовых, если за 4 года вклад вырос на 167 400 рублей?
13. Известно, что банк начисляет простые проценты по ставке 25% годовых. Определите минимальное число лет, по истечении которых первоначальный вклад увеличится в 2 раза?
14. Определите годовую процентную ставку ( банк начисляет простые проценты), если первоначальный вклад величиной 23 500 рублей за 6 лет увеличился на 38 070 рублей?
15. В банк внесен вклад 64 000 рублей на 3 года. Определите ставку процента, если через 3 года на счету вкладчика оказалось 216 000 рублей.
16. Известно, что ставка банковского процента равна 25%. Определит, через сколько лет начальный вклад 216 000 рублей возрастет до 421 875 рублей.
17. Цена некоторого товара снижается ежегодно на 10%. На сколько процентов по сравнению с первоначальной снизится стоимость товара через четыре года?
18. В течение января цена на яблоки выросла на 20%, а в течение февраля — на 30%. На сколько процентов поднялась цена за 2 месяца?
19. Изобретение Иванова даёт экономию 40%, Петрова — 30%, а Сидорова — 20%. Сколько процентов составит общая экономия? (Применение одного изобретения не влияет на эффективность других.)
20. Пётр открыл вклад «Сюрприз» на три года. Договор предусматривает следующую схему начисления процентов: за первый год — 8%, в каждом следующем году ставка повышается на 4 процентных пункта. Определите, на сколько процентов вырастет вклад Петра за три года.
21. По оценкам экспертов цена новой модели сотового телефона снижается за первый год на 15%, за второй — на 10%, за третий — на 5%. Сколько будет стоить через три года сотовый телефон, начальная цена которого равнялась 250 евро?
22. При оплате услуг через платежный терминал взимается комиссия 5%. Терминал принимает суммы, кратные 10 рублям. Аня хочет положить на счет своего мобильного телефона не меньше 300 рублей. Какую минимальную сумму она должна положить в приемное устройство данного терминала.
 |


Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.