Сборник "Решение планиметрической задачи при подготовке е ЕГЭ"

. Абдулино 2018г.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Содержание

 

1.     Введение

2.     Критерии оценивания  планиметрических задач

3.     Основные формулы для решения задач

4.     Решение  задач типа: «Многоугольники и их свойства»

5.     Решение  задач типа: «Окружности и системы окружностей»

6.     Решение  задач типа: «Окружности и треугольники»

7.     Решение  задач типа: «Окружности и четырёхугольники»

7. Практикум по решению задач

8. Задачи с ответом

9. Задачи для самостоятельного решения

 

 

 

 

 

 

 

 

 

 

 

В планиметрических заданиях заметное структурное и содержательное изменение произошло в 2014 году. В пункте а теперь нужно доказать геометрический факт, в пункте б – найти (вычислить) геометрическую величину.

С точки зрения разработчиков включение проверяемого элемента на доказательство в задание 16 должно повысить уровень подготовки школьников. Кроме того, такое доказательство является естественным продолжением практики использования заданий на доказательство в экзамене за курс основной школы. По фактическим данным выполнения задание 16 является границей, разделяющий высокий и повышенный уровень подготовки участников ЕГЭ.

При  подготовке  к сдаче ЕГЭ и обучении решению задач 16 следует  отметить,  что  для  выполнения первого  пункта  задачи  нужно  помнить основные  определения,  теоремы  и  следствия из них, а также признаки и свойства  геометрических  фигур.  В  основном первая  часть  решения  сводится к  доказательству  одного  из  следующих  свойств приведенной  в  условии  геометрической конфигурации:

а) подобия указанных треугольников;

б)  параллельность  или  перпендикулярность указанных прямых;

в)  равенство указанных углов, отрезков, площадей или их заданное отношение;

г)  принадлежность  указанной  фигуры к определенному типу:

·        треугольник  является  прямоугольным, равнобедренным и т.д.;

·        четырехугольник  является  описанным или вписанным;

·        четырехугольник  обладает  признаками  параллелограмма,  ромба,  трапеции и т.д.;

·        точка  равноудалена  от  вершин  или сторон  многоугольника,  то  есть  является центром вписанной или описанной окружностей;

·        прямая  содержит  указанные  точку или отрезок.

 

Памятка решения геометрических задач.

1)    Чтение условия задачи.

2)    Выполнение чертежа с буквенными обозначениями.

3)    Краткая запись условия (база знаний)

4)    Деталировка – вычерчивания отдельных деталей на дополнительных чертежах; исходная сложная задача разбивается на несколько простых

5)    Составление цепочки действий

6)    Реализация алгоритма решения

7)    Проверка правильности решения (логику доказательства, найденные величины имеют геометрический смысл)

8)    Ответ

 

 

 

Содержание критерия, задание №16	Баллы
Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б	3
Обоснованно получен верный ответ в пункте б ИЛИ имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки	2
Имеется верное доказательство утверждения пункта а, ИЛИ при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б с использованием утверждения пункта а, при этом пункт а не выполнен	1
Решение не соответствует ни одному из критериев, перечисленных выше	0
Максимальный балл	3

 

 

1.      «Многоугольники и их свойства»

2.      «Окружности и системы окружностей»

3.      «Окружности и треугольники»

4.      «Окружности и четырёхугольники»

1. Основные определения и теоремы планиметрии

 

 

 

 

Задания № 16. ЕГЭ.(Математика. 50 вариантов типовых тестовых заданий; под ред. И.В. Ященко.  М.:  Издательство «Экзамен»,

 

 

1) На отрезке BDвзята точка С. Биссектриса BL равнобедренного треугольникаABCc основанием ВС является боковой стороной равнобедренного треугольника BLD с основанием BD.

а) Докажите, что треугольникDCL равнобедренный.

б) Известно, что  cos∠ABC = ¹/₆. В каком отношении прямаяDL делит сторону AB?

 

 

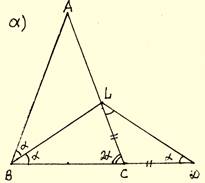По условию:  ∠ВDL=∠LВD= αи

∠АСВ=∠АВС=2α.

Так как  ∠LСВ – внешний  дляLСD, то  2α = α +∠СLD, ∠СLD= α  = ∠LDС,  LСD– равнобедренный.

Доказано.

 

1)    . По условию: 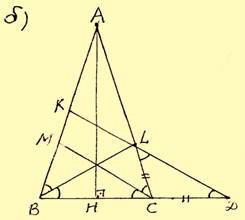cos∠B = ¹/₆,

 тогдаВН = ɑ,  АВ = 6ɑ,ВС = 2ɑ.

2)  . ВL– биссектриса, 

LC : LA = BC : AB = 1 : 3, 

LC = ¹/₄AC = 1.5ɑ=CD; AL =³/₄  AC = 4.5ɑ.

3)  . MC– биссектрисаравнобедренного,  BM = CL = 1.5ɑ( и MC||KD.

4)   . По теореме о пропорциональных отрезках:

=  ;   =  ;MK = ɑ;BK = (   +   )ɑ =  ɑ;

AK = (6–  )ɑ=  ɑ;   =  = .

Ответ: AK : KB = 9 : 7.

 

№2. СторонаCD прямоугольника ABСD касается некоторой окружности в точке М. Продолжение стороны AD пересекает окружность в точках Pи Q, причем точка Pлежит между точками D и Q. Прямая  BCкасается окружности, а точка Q лежит на прямой BM.

а) Докажите, что ∠DMP = ∠CBM.

б) Известно, чтоCM = 17 и CD = 25. Найдите сторону AD.

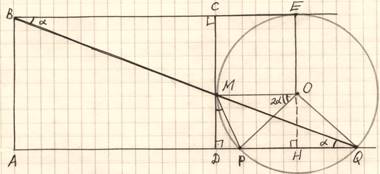
а). ∠CBM=∠BQA= α, (как накрест лежащие при  ВСǁAQ),

∠MQP=⌒MP– вписанный;

∠MOP=⌒MP– центральный; ВMOP:

∠OMP=∠OPM= 90^ᵒ–.

ТаккакOM⊥CD ,  то  ∠DMP = 90^ᵒ –∠OMP = 90^ᵒ – ) == ∠CBM.

Доказано.

б)1. CMOE – квадрат, т.к.  ∠C =∠E =∠M = 90^ᵒ;CM =EO = RиCE=MO =R.

     По условию  AB =CD = 25,  CM = R = 17,  MD= 8.

 

     2.  Проведем радиусOQ.  Так как DMOH–прямоугольник,  то OH = MD = 8.

PH² = OP²– OH² = 17² – 8² = 225, PH = 15.DH = MO = R =17.

DP = DH – PH = 17 – 15 = 2.

 

    3.  BCM иMDPподобны, (∠CBM = ∠DMP = , ∠C = ∠D = 90^ᵒ), 

=  ;BC =  = 68.AD = 68.

Ответ: AD = 68.

 

№3.Отрезок, соединяющий середины  Mи N оснований  BCиAD соответственно трапеции  ABCD, разбивает её на две трапеции, в каждую из которых можно вписать окружность.

а) Докажите, что трапеция  ABCD равнобедренная.

б) Известно, что радиус этих окружностей равен 3, а меньшее основание  BCисходной трапеции равно 10. Найдите радиус окружности, касающейся боковой стороны AB, основания ANтрапеции  ABMNи вписанной в неё окружности.

 

По свойству описанного четырехугольника:

BM+AN = AB+MN,  MC + ND = CD + MN.

По условию: BM = MC,  AN = ND. 

BM+AN = MC+ND,  AB +MN=CD +MN, AB = CD.

Доказано.

 

б). Из п. а)следует, что трапеции  ABMNи DCMNсимметричны относительно MN,  и MN⊥АВ, MN⊥BC.Рассмотрим прямоугольную трапецию ABCM:

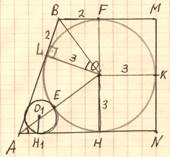ВМ =5, R = 3.  Найти: О₁Н_{1 =} r = ?

1). Проведем радиусOL⊥ABи отрезокOВ;

По  свойству  касательных  BF = BL = 5 – 3= 2,

BO²= 3² + 2² = 13,  BO =  .

BOиAO – биссектрисы,  ∠A + ∠ B = 180^ᵒ,

ABO–прямоугольный.   ALO =AHO.

2). Треугольники AOB, ALO, AHO, OLB–подобны.

OL² = ALхLB,AL = иAН = ; АO² = AL²+LО²=;AО =  .

Из подобия  AOHи AO₁H₁ AO :AO₁= OH :O₁H_{1 ,}= 3 : r, причем

AO₁ = АО – 3– r.r= – 18 – 6r ,r = .

Ответ: r = .

№ 4Две окружности касаются внутренним образом. Третья окружность касается первых двух и их линии центров.

а) Докажите, что периметр треугольника с вершинами в центрах трех окружностей равен диаметру наибольшей из этих окружностей.

б) Найдите радиус третьей окружности, если известно, что радиусы первых двух равны 4 и 1.

 

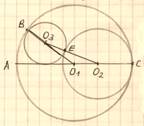а). Так как точка касания окружностей лежит на линиих центров, получим три уравнения: O₁O₂ = O₁C–O₂C = R₁–R₂;

O₁O₃ = O₁B – O₃B = R₁– R₃;     O₂O₃ = O₂E+O₃E = R₂+R₃;

Сложим левые и правые части этих уравнений и получим:

O₁O₂ + O₁O₃+ O₂O₃=2R₁.              Доказано.

б). По условию: R₁=O₁C=O₁B = 4; R₂=O₂E=O₂C = 1.

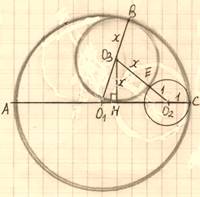1. Проведем O₃H⊥O₁O₂;  O₃H= O₃B= O₃E= R₃ = x.

O₁O₂ = R₁– R₂= 3;  O₁O₃ = R₁– R₃=4– x;

O₂O₃ = R₂+ R₃ = x + 1;O₂H= O₁O₂ – O₁H =3– O₁H.

2. ВO₁O₃H: (O₁H)² = (O₁O₃)²– (O₃H)²= (4– x)²– x ²= =16 –8x, O₁H=2; x2, O₁O₃O₁O₂.

3. ВO₂O₃H: (O₂O₃)² =(O₂H)²+(O₃H)². Получим:

(3– 2)²+x ²= (x+ 1)².

12 = 24 – 10x;  25x ² = 0,   = 1,92.

Ответ: R₃1,92.

 

Вариант № 5

 

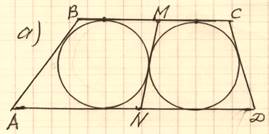
В параллелограмм вписана окружность.

а) Докажите, что этот параллелограмм – ромб.

б) Окружность, касающаяся стороны ромба, делит её на отрезки, равные 3 и 2. Найдите площадь четырехугольника с вершинами в точках касания  окружности со сторонами ромба.

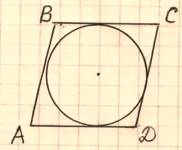
а)ABCD – параллелограмм, AB=CD, BC= AD.

ABCD – описанный  четырехугольник,

AB+CD = BC+AD,

2AB = 2CD = 2BC = 2AD,

AB = CD = BC = AD,

ABCD– ромб.

Доказано.

 

б)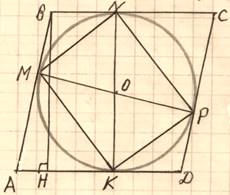1.  M, N, P, K – точки касания, ON⊥BC, OK⊥AD;OM⊥AB, OP⊥CD.AB//CD,  BC//AD,  NKиMP–диаметры,MNPNPKPKMKMN_MNPK = MK·KP.

2. ПроведемBH⊥CD.  BM = BN =HK =2,

AM = AK = 3, AH = 1,  AB = 5, cosBAH =1/5, cosKDP=–1/5,таккакA +D =

Найдем MK по теореме косинусов в АMК: 

MK² = 3² +3² – 2·3·3· 1/5 = 15,6;

аналогично в DPК: PK² = 2² + 2² – 2·2·2·(–1/5) = 9,6;

_MNPK = MK·KP =  = = 4.8 .

                                                               Ответ: 4.8 .

 

Вариант № 6

 

На катетах ACиBC прямоугольного треугольника ABCвне треугольника построены квадраты ACDEиBFKC. Точка M – середина гипотенузы AB,  H – точка пересечения прямыхCMиDK.

а) Докажите, чтоCMIDK.

б) НайдитеMH, если известно, что катеты треугольника ABCравны 130 и 312.

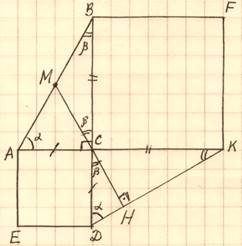
а).ACB =DCK–по двум катетам(так какACDEиBFKC – квадраты, тоAC=CDи BC=CK). ∠BAC =∠КDC = α,  ∠ABC = β, иα+β= 90^ᵒ

CM–медиана прямоугольного треугольника

CM = AM = MB∠MBC = ∠MCB = β.

∠MCB = ∠HCD = β– вертикальные углы.

В  DCH∠CHD= 180^ᵒ– (α + β) = 90^ᵒ,

CMIDK.

Доказано.

 

б)MH = CM + CH.МедианаCMравна половине гипотенузы  AB.

AB² = AC² + CB² =130² + 312² = 114244,  AB = 338,  CM = 169.

CH – высота прямоугольного треугольника DCK

CH = CD·CK: DK = 130·312: 338 =120.   MH = CM + CH = 169 + 120 = 289.

Ответ: MH= 289.

Вариант № 9

 

Окружность, построенная на стороне ADпараллелограмма  ABСD как на диаметре, проходит через точку пересечения диагоналей параллелограмма.

а) Докажите, что ABСD – ромб.

б) Эта окружность пересекает сторону AB в точке M, причем AM:MB = 3:1. Найдите диагональ AC, если известно, что AD = 2˅͞2.

 

а).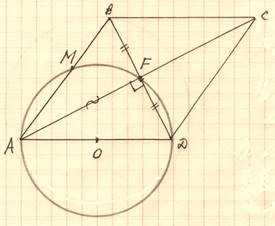1. F – точка пересечения диагоналей параллелограмма. Так как AD – диаметр, то

∠AFD =90^ᵒ.

2. ABF  =ADF(по дум катетам),

AB=AD, AB=BC = CD=AD и параллелограмм  ABСD – ромб.

Доказано.

б). ПустьBM = a, MA = 3a, AB = 4a;

BF = FD = b, BD = 2b.

1.   По теореме о двух секущих имеем:  BA·BM = BD·BF,  4a²=2b², b²= 2a².

2.    ТаккакABСD – ромб, тоAD = AB = 4a= 2˅͞2 ,   a= ˅͞2 /2,  a² =  , b²= 1.

3.   AFD– прямоугольный, по теореме ПифагораAF² =AD²–FD²= 16a²–b² = 7,

ð  AF =˅͞7   и   AC= 2˅͞7 .

Ответ: AC= 2˅͞7 .

 

Вариант № 10

 

Точки  В₁и С₁лежат на сторонах соответственно АС и АВ треугольника АВС, причем АВ₁: В₁С = АС₁ : С₁В. Прямые ВВ₁и СС₁ пересекаются в точке О.

а)Докажите, чтопрямая АО делит пополам сторону ВС.

б) Найдите отношение площади четырехугольника АВ₁ОС₁ к площади треугольника АВС, если известно, что АВ₁ : В₁С = АС₁ : С₁В = 1 : 4.

 

а)По теореме Чевыимеем:

(СВ₁ : В₁А )· ( АС₁: С₁В) · (ВА₁ :А₁С) = 1.

По условиюАВ₁ : В₁С = АС₁ : С₁В = m:n,

Поэтому (СВ₁ : В₁А)·( АС₁ : С₁В)= ·=1ВА₁ : А₁С = 1, ВА₁= А₁С.

Доказано.

 

б) = –;

1.  Так как  АВ₁ : В₁С = АС₁ : С₁В = 1 : 4, то и

::= 1 : 4.

Если= S,  то  =S,  а = =S.

Так как  АВ₁ :АС = АС₁ :АВ= , то  В₁С₁ ВСВ₁ АС₁и САВ подобны, а также подобны  ВОС и  В₁ОС₁( по двум равным углам).  

В₁О : ВО = В₁ С₁ : СВ=   ,  и =   = (·)SS. 

 = –  =S –  S =S,  : = 1 : 15.

 

Ответ:  :  = 1 : 15.

 

Вариант № 15

 

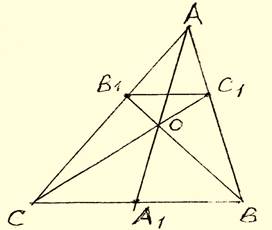
Медианы  АА₁, ВВ₁ и СС₁ треугольника АВС пересекаются в точке М. Точки А₂,  В₂ и С₂ – середины отрезков МА, МВ и МС соответственно.

а) Докажите, что площадь шестиугольника  А₁В₂С₁А₂В₁С₂  вдвое меньше площади АВС.

б) Найдите сумму квадратов всех сторон этого шестиугольника, если известно, что АВ = 4, ВС = 7 и АС = 8.

 

а)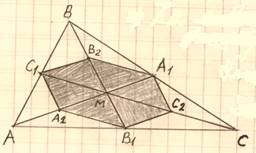Медиана делит треугольник на два равновеликих

=S₁;   =S₂;   =S₃;=S₄;

=S₅;=S₆;

Тогда= S₁+ S₂+S₃  +S₄  + S₅ + S₆.

= 2(S₁+ S₂  +S₃  +S₄  + S₅ + S₆).  

= .              Доказано.

 

б)1.Заметим, что  А₁В₂ =  А₂В₁ =    МС= c, как средние линии BCMиАCM.

Аналогично: B₁C₂ =B₂C₁ =    МA= aиС₁А₂ =  С₂А₁ =    МВ= b, причем по свойству медиан:  c= СС₁ ,  a= АА₁ , b = BB₁ .

2.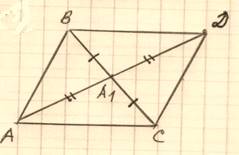Продлим медиану  АА₁  на её длину, получим параллелограмм ABDCcдиагоналями ADиBC.

Применив теорему косинусов для ABCиABD, получим, что AD²+BC²=AB²+BD²+DC²+AC²,

AD²=4(AA₁)²= 2AB² +2AC ²– ВС²,

(АА₁)² =  (2АВ² + 2АС² – ВС²). 

Аналогично получим: 

(ВВ₁)² =  (2АВ² + 2ВС² – АС²)  и  (СС₁)² =  (2ВС² + 2АС² – АВ²),

(АА₁)²+ (АА₁)²+(СС₁)²= (АВ² + ВС²+ АС²).   Сумма квадратов сторон шестиугольника равна:  2a² + 2b²+ 2c²=((АА₁)²+ (АА₁)²+ (СС₁)²) =

·(АВ² + ВС² + АС²) = (16 + 49 + 64) =  = 21,5.

Ответ:21,5.

 

Вариант № 16

 

Окружность с центромО вписана  угол, равный 60^ᵒ. Окружность большего радиуса с центром О₁ также вписана в этот угол и проходит через точку О.

а) Докажите, что радиус второй окружности вдвое больше радиуса первой.

б) Найдите длину общей хорды этих окружностей, если известно, что радиус первой окружности равен 2˅͞3.

 

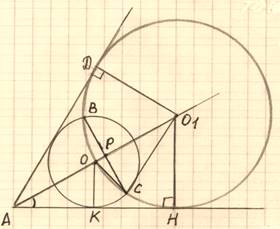а)Так как окружности вписаны в уголА, то АО₁– биссектриса угла А. 

∠О₁АН =30^ᵒ,  ОК = R,   О₁О = О₁Н = R₁;AO₁ = 2R₁, AO= 2R, AO₁ = AO + О₁О, 2R₁ = 2R + R₁,R₁ = 2R.

 

Доказано.

 

б)R =2˅͞3 , R₁=4˅͞3 .ВС- общая хорда.

ТочкиВ и С симметричны относительно биссектрисы  АО₁ВР = РС и  ВС⊥АО₁.

1.   Рассмотрим  О₁ОC.

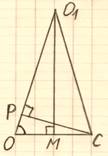О₁О= О₁С = R₁=4˅͞3;ОC = R =2˅͞3 ,OM= МС= ˅͞3 ;

О₁М²=О₁О²–ОМ² =48 – 3 = 45  и  О₁М = 3˅͞5 .

2.  ОО₁М иОCР подобны (∠Р = ∠М = 90^ᵒ,  ∠О– общий),  ОО₁ : ОC = О₁М :CР,CР = (ОC·О₁М) :ОО₁ =

(2˅͞3 ·3˅͞5 ) : 4˅͞3  = 1,5˅͞5  ,  ВР = 2СР = 3˅͞5 .

 

Ответ: 3˅͞5 .

 

 

Вариант № 20

 

  Две окружности пересекаются в точках  PиQ. Прямая, проходящая через точку P, второй раз пересекает первую окружность в точкеА, а вторую – в точке D.  Прямая, проходящая через точку Qпараллельно AD, второй раз пересекает первую окружность в точке B, а вторую – в точке C.

а) Докажите, что четырехугольник ABCD – параллелограмм.

б) Найдите отношение ВР : РС, если радиус первой окружности вдвое больше радиуса второй.

 

а)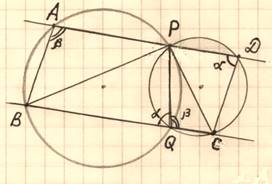Обозначим ∠PQB =α, ∠PQС=β, причем α+ β= 180^ᵒ  (смежные).

Так как четырехугольники APQBиPDCQ – вписанные, то ∠PQB+ ∠PАB = 180^ᵒ и     ∠PQС+ ∠PDB = 180^ᵒ,

∠PАB =β,  а ∠PDС =α

∠PАB + ∠PDС = α+ β= 180^ᵒ, а это односторонние углы ABDC, а по условию ADBC, ABCD – параллелограмм.

                                                                                               Доказано.

 

б)PQBи  PDС– вписанные и по теореме синусов:

PB:sin∠PQB = 2R₁, PC : sin∠PQC = 2R₂, где R₁и R₂ соответственно радиусы первой и второй окружностей. PB = 2R₁sin∠PQBи PС = 2R₂ sin∠PQС.

Так как ∠PQB+ ∠PQB= 180^ᵒ, то sin∠PQB =sin∠PQС = sinα.

По условию R₁ = 2R₂,ВР : РС = 4R₂ sinα:2R₂ sinα=2.

                                                                                            Ответ: ВР: РС=2.

 

 

Вариант № 32

 

Противоположные стороны ADиBC  четырехугольникаABCD параллельны. Через вершиныВи D проведены параллельные прямые, пересекающие диагональ АС в точках Mи Nсоответственно. Оказалось, что АМ = MB = NC.

а) Докажите, что ABСD – параллелограмм.

б) Найдите отношение площади четырехугольника BMDN к площадипараллелограмма ABСD.

 

а)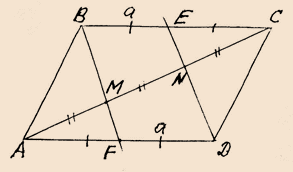 1. По условию ADBC и  BFED

FBED – параллелограмми BE = FD = a.

2. По теореме Фалеса:

т.к. AM = MNиBFED, AF = FD = a, тогдаAD = 2a.

т.к. MN= СNиBFED, BE = EC = a, тогдаBC = 2a.AD =BC, ADBC, 

ABСD – параллелограмм.

Доказано.

 

б)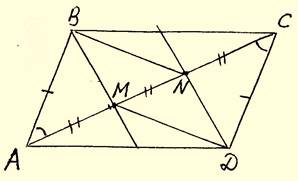Так как медиана делит треугольник на два равновеликих, получим:

 = = S;  = = S,

= 3S, атак как AС – диагональ параллелограмма, то = 6S.

 = = S,(ABM=CDN по I признаку). = = S,

= 2S, : =2S : 6S = 1 : 3.

1 : 3.

 

 

Вариант № 38

 

На сторонах AСиBС треугольника  АBС вне треугольника построены квадраты  ACDEи BFKC. Точка M– середина стороны AB.

а) Докажите, чтоCM = DK.

б) Найдите расстояния  от точки Mдо центров квадратов, если AC = 6, BC = 10и∠ACB =30^ᵒ.

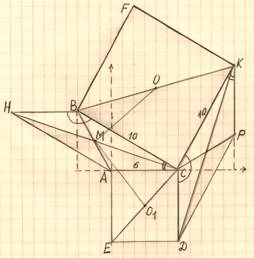а)Проведем HBAC, HBAC; KPCD, KPCD; получим параллелограммы ACBHи CDPK, в которых AC = CDиKC = BC(из условия).

∠ACD+∠BCK=30^ᵒ+ 30^ᵒ = 180^ᵒ

∠ACB+∠DCK= 180^ᵒ.

∠CBH+∠ACB= 180^ᵒ, как односторонние углы.  ∠CBH=∠DCK. Аналогично ∠ACB =∠CKP.

Параллелограммы ACBHи CDPKравны, так как равны все соответственные стороны и углы.

CH = DK, а так как точка M– середина стороны AB, то CM = CH=DK.

                                                Доказано.

 

б)Для нахождения MO иMO₁применим метод координат.

Начало координат – точкаА(0;0), ось Ox–вдоль АС, ось Oy⊥АС.

Найдем координаты нужных точек из условия ( АС = 6, ВС = 10, ∠ACB =30^ᵒ,

О₁– середина СЕ, О– середина ВК,М– середина АВ):

С(6; 0), Е( 0; –6), О₁(3; –3),В(6–5; 5), К(11; 5), О(; ), М(;).

МО²=()² + ()²= 49, МО = 7.

МО₁²= (–)² + ()²= 49, МО₁ = 7.

Ответ:МО =МО₁ = 7.

 

 

 

 

Вариант № 40

 

Пятиугольник ABСDЕ вписан в окружность. Из вершиныА опущены перпендикуляры AF, AH, APиAQ на прямые DE, BE, CDиBC соответственно.

а) Докажите, что∠FAH = ∠PAQ.

б) НайдитеAH, если AF = ɑ, AP = bиAQ = c.

 

а)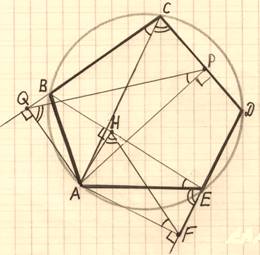Докажем, что FAHи PAQподобны.

1. Так как ∠AFЕ = ∠AHЕ = 90^ᵒ, то AFЕH– вписанный в окружность с диаметром AЕ,

∠AFH= ∠AЕHкак вписанные углы. Также

∠AЕH= ∠AЕB= ∠AСB как вписанные углы.

∠AFH= ∠AСB(1).

2.  ∠AQС = ∠AРС = 90^ᵒ, и AQСР – вписанный в окружность с диаметром AС,

∠AСQ = ∠AРQ, ∠AFH=∠AРQ (2).

3. Аналогично ∠AHF= ∠AЕF.

Заметим, что ∠AЕF +∠AЕD= 180^ᵒ (смежные) и ∠AЕD+∠AСD= 180^ᵒ (AСDЕ вписанный),

∠AЕF = ∠AСD= ∠AСР;  ∠AСD= ∠AQР, т.к. AQСР – вписанный. 

∠AHF=∠AQР    (3).   Из (2) и (3) следует, что FAHи PAQподобны.

∠FAH = ∠PAQ.

Доказано.

 

б)Так как FAHи PAQподобны, то AH :AQ = AF :AP, AH = = .

 

Ответ: AH= .

Решу ЕГЭ

1.      Задание 16 № 511418

Диагональ AC прямоугольника ABCD с центром O образует со стороной AB угол 30°. Точка Eлежит вне прямоугольника, причём 

а) Докажите, что 

б) Прямая OE пересекает сторону AD прямоугольника в точке K. Найдите EK, если известно, что BE = 20 и CE = 12.

Решение.

а) По теореме о внешнем угле треугольника  Поэтому

Значит, точки B, E, C, O лежат на одной окружности. Вписанные в эту окружность углы CBE и COE опираются на одну и ту же дугу, следовательно, 

б) По теореме косинусов

 

Вписанные углы BEO и CEO опираются на равные хорды BO и CO, значит, EO — биссектриса угла BEC. Пусть M — точка её пересечения со стороной BC. По формуле для биссектрисы треугольника получаем:

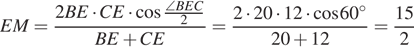
По свойству биссектрисы треугольника  значит, 

По теореме о произведении пересекающихся хорд  откуда находим, что 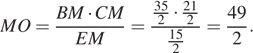 Треугольники COM и AOK равны по стороне и двум прилежащим к ней углам, поэтому OK = OM. Следовательно, EK = EM + 2OM = 

 

Ответ: 

 

 

2.      Задание 16 № 505425

Высоты BB₁ и CC₁ остроугольного треугольника ABC пересекаются в точке H.

а) Докажите, что ∠AHB₁ = ∠ACB.

б) Найдите BC, если AH = 4 и ∠BAC = 60°.

Решение.

а) В четырёхугольнике AC₁HB₁ углы C₁ и B₁ — прямые, следовательно, около этого четырёхугольника можно описать окружность, причём AH — её диаметр. Вписанные углы AC₁B₁и AHB₁ опираются на одну дугу, следовательно, ∠AHB₁ = ∠AC₁B₁.

Углы BC₁C и BB₁C — прямые, значит, точки B, C, B₁ и C₁ лежат на окружности с диаметром BC. Следовательно,

Получаем, что ∠ACB = ∠AHB₁.

б) В треугольнике AB₁C₁ диаметр описанной окружности AH = 4, откуда

В прямоугольном треугольнике BB₁A имеем:

В прямоугольном треугольнике CC₁A имеем:

Получаем, что  Треугольники ABC и AB₁C₁ имеют общий угол A и следовательно, они подобны. Тогда  Значит,

Ответ: 

 Приведём другое решение.

а) Поскольку AA₁ — перпендикуляр к ВС, а BB₁ — перпендикуляр к AС (см. рис.), углы AHB₁и ACB равны как углы со взаимно перпендикулярными сторонами.

б) Сторона треугольника, величина противолежащего ей угла и отрезок высоты, проведённой из вершины этого угла в точку пересечения высот треугольника, связаны соотношением:  откуда 

3. Задание 16 № 514536

В остроугольном треугольнике ABC проведены высоты AK и CM. На них из точек M и K опущены перпендикуляры ME и KH соответственно.

а) Докажите, что прямые EH и AC параллельны.

б) Найдите отношение EH и AC, если 

Решение.

а) AMKC — вписанный четырехугольник, поскольку  — все точки лежат на окружности с диаметром AC. Аналогично MKEH — вписанный, причем в окружность с диаметром MK. Значит,

откуда 

б) Обозначим за O точку пересечения AK и MC. Тогда   Поэтому KOC — равнобедренный прямоугольный треугольник, и его высота KHсовпадает с его медианой, то есть H — середина OC. Аналогично E — середина OA, поэтому EH — средняя линия треугольника AOC и 

 

Ответ: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4. Задание 16 № 517751

Окружность, вписанная в трапецию ABCD, касается ее боковых сторон AB и CD в точках M и Nсоответственно. Известно, что AM = 6MB и 2DN = 3CN.

а) Докажите, что AD = 3BC.

б) Найдите длину отрезка MN, если радиус окружности равен 

Решение.

а) Пусть окружность касается оснований BC и AD в точках K и L соответственно, а ее центр находится в точке O.

Лучи AO и BO являются биссектрисами углов BAD и ABC соответственно, поэтому

то есть треугольник AOB прямоугольный. Аналогично, треугольник COD тоже прямоугольный. Пусть BM = x, CN = y, тогда AM = 6x, DN =

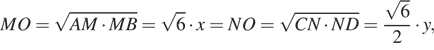
откуда y = 2x. Получаем: BK = BM = x, AL = AM = 6x, CK = CN = 2x, DL = DN = 3x, BC = BK + KC = 3x, AD = AL + LD = 9x, то есть AD = 3BC.

б) Заметим, что  поэтому 

Пусть прямые AB и CD пересекаются в точке P, а прямые MN и PO пересекаются в точке Q. Тогда треугольники BPC и APD подобны, поэтому AP = 3BP, AB = 2BP, BP =, PN = PM = Прямая POявляется серединным перпендикуляром к MN. В прямоугольном треугольнике OMP получаем:

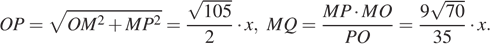
Значит, 

Ответ: б) 18.

 

 

5. Задание 16 № 517751

Окружность, вписанная в трапецию ABCD, касается ее боковых сторон AB и CD в точках M и Nсоответственно. Известно, что AM = 6MB и 2DN = 3CN.

а) Докажите, что AD = 3BC.

б) Найдите длину отрезка MN, если радиус окружности равен 

Решение.

а) Пусть окружность касается оснований BC и AD в точках K и L соответственно, а ее центр находится в точке O.

Лучи AO и BO являются биссектрисами углов BAD и ABC соответственно, поэтому

то есть треугольник AOB прямоугольный. Аналогично, треугольник COD тоже прямоугольный. Пусть BM = x, CN = y, тогда AM = 6x, DN =

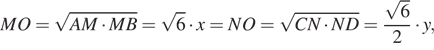
откуда y = 2x. Получаем: BK = BM = x, AL = AM = 6x, CK = CN = 2x, DL = DN = 3x, BC = BK + KC = 3x, AD = AL + LD = 9x, то есть AD = 3BC.

б) Заметим, что  поэтому 

Пусть прямые AB и CD пересекаются в точке P, а прямые MN и PO пересекаются в точке Q. Тогда треугольники BPC и APD подобны, поэтому AP = 3BP, AB = 2BP, BP =, PN = PM = Прямая POявляется серединным перпендикуляром к MN. В прямоугольном треугольнике OMP получаем:

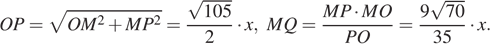
Значит, 

Ответ: б) 18.

 

 

6. Задание 16 № 507237

Две окружности касаются внутренним образом. Третья окружность касается первых двух и их линии центров.

а) Докажите, что периметр треугольника с вершинами в центрах трёх окружностей равен диаметру наибольшей из этих окружностей.

б) Найдите радиус третьей окружности, если известно, что радиусы первых двух равны 4 и 1.

Решение.

а) Пусть АВ — диаметр большей из трёх окружностей, О — её центр, O₁ — центр окружности радиуса r у касающейся окружности с диаметром АВ в точке А, O₂ — центр окружности радиуса R, касающейся окружности с диаметром АВ в точке С, окружности с центром O₁ — в точке D, отрезка АВ — в точке Е. Точки О, O₂ и С лежат на одной прямой, поэтому OO₂ = ОС − O₂С = ОС − R. Аналогично ОО₁ = OA − О₁А = ОА − r и O₁O₂ = O₁D + O2D = r + R. Следовательно, периметр треугольника OO₁O₂ равен

б) Пусть OA = 4, r = 1. Тогда O₂Е = R, O₁O₂ = 1 + R, OO₁ = OA − О₁А = 4 − 1 = 3, OO₂ = ОС − O₂С = 4 − R. Из прямоугольных треугольников O₁O₂Е и OO₂Е находим, что

а так как О₁E = OO₁ + ОЕ, то  Из этого уравнения находим, что  (это значит, что диаметр искомой окружности равен радиусу наибольшей из трёх окружностей, то есть точка Е совпадает с О).

 

Ответ: 

 

 

 

 

 

 

7. Задание 16 № 509024

В прямоугольном треугольнике ABC с прямым углом C известны стороны AC = 15, BC = 8. Окружность радиуса 2,5 с центром O на стороне BC проходит через вершину C. Вторая окружность касается катета AC, гипотенузы треугольника, а также внешним образом касается первой окружности.

а) Докажите, что радиус второй окружности меньше, чем  длины катета 

б) Найдите радиус второй окружности.

Решение.

а) Пусть  — центр второй окружности,  и  — её точки касания со сторонами  и соответственно, а точка  — проекция точки  на  Имеем: следовательно,  Тогда Поэтому  что и требовалось доказать.

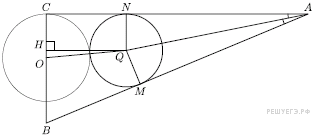
б) Пусть  — радиус второй окружности. Рассмотрим прямоугольный треугольник 

По теореме Пифагора  откуда:

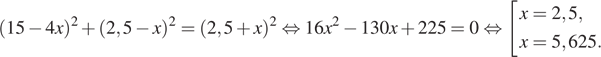
Условию  удовлетворяет только  Кстати, отсюда следует, что точки  и совпадают.

 

Ответ: 2,5.

 

 

 

 

8. Задание 16 № 511589

Точка О — центр окружности, вписанной в треугольник ABC. На продолжении отрезка AO за точку О отмечена точка K так, что BK = OK.

а) Докажите, что четырехугольник ABKC вписанный.

б) Найдите длину отрезка AO, если известно, что радиусы вписанной и описанной окружностей треугольника ABC равны 5 и 15 соответственно, а OK = 8.

Решение.

а) Пусть  Так как О — центр вписанной окружности треугольника  то АО, ВО — биссектрисы углов А и В, значит,  Угол BOKвнешний для треугольника  поэтому  (см. рисунок).

Так как BK = OK (по построению), то  тогда  Углы CBK и KAC опираются на один и тот же отрезок CK и равны друг другу:  Тогда по признаку, связанным со свойством вписанных углов, точки А, В, К, С лежат на одной окружности.

б) Обозначим через r, R радиусы вписанной и описанной окружностей треугольника  Пусть H — проекция точки О на сторону AB (см. рис.), тогда  Так как точки А, В, К, С лежат на одной окружности, то радиус описанной окружности треугольника совпадает с радиусом описанной окружности треугольника  и равен R. Из треугольника  по теореме синусов: Тогда

Так как то 

 

Ответ: 18,75.

 

 

 

 

 

 

9. Задание 16 № 514719

Отрезок, соединяющий середины M и N оснований BC и AD соответственно трапеции ABCD, разбивает её на две трапеции, в каждую из которых можно вписать окружность.

а) Докажите, что трапеция ABCD равнобедренная.

б) Известно, что радиус этих окружностей равен 3, а меньшее основание BC исходной трапеции равно 10. Найдите радиус окружности, касающейся боковой стороны AB, основания AN трапеции ABMN и вписанной в неё окружности.

Решение.

а) Из описанности трапеций следует, что  и  Поскольку  и  получаем что 

б) Очевидно, при этих условиях отрезок MN является высотой трапеции и имеет длину 6. Пусть AN = t, тогда из описанности трапеции BMNA, следует,  откуда  Опуская высоту BK, получим  откуда  Решая это уравнение, получаем  и 

Обозначим O — центр окружности, вписанной в BMNA, центр второй окружности —  их проекции на сторону AB за T и  соответственно, радиус второй окружности обозначим r. Тогда  — трапеция, в которой   

Опустим из O перпендикуляры OL и OH на BM и MN соответственно. Тогда OLMH — квадрат со стороной 3, поэтому  а  Из подобия треугольников ATO и  находим тогда, что  и 

Теперь, опустим перпендикуляр  на OT. Тогда  получаем уравнение:

Из двух корней подходит только меньший, поскольку 

 

Ответ: 

 

 

 

 

 

10. Задание 16 № 511403

Дан четырёхугольник 

а) Докажите, что отрезки  и  соединяющие середины его противоположных сторон, делят друг друга пополам.

б) Найдите площадь четырёхугольника , если ,  

Решение.

а) Пусть  и  — середины сторон  и  четырёхугольника соответственно. Тогда  и  — средние линии треугольников  и  Значит,  и  поэтому  — параллелограмм. Его диагонали  и  делят друг друга пополам, что и требовалось доказать.

б) В треугольнике  имеем:

Значит,  Тогда  поэтому треугольник  прямоугольный треугольник с прямым углом при вершине  Четырёхугольник  — прямоугольник, поэтому

Отрезок  является средней линией треугольника  поэтому  Аналогично  Тогда, имеем:

Где  — искомая площадь четырёхугольника  Аналогично Поэтому

Следовательно,

Ответ: 

 

 

 

11. Задание 16 № 505249

В равнобедренном треугольнике ABC с углом 120° при вершине A проведена биссектриса BD. В треугольник ABC вписан прямоугольник DEFH так, что сторона FH лежит на стороне BC, а вершина E —  на стороне AB.

а) Докажите, что FH = 2DH.

б) Найдите площадь прямоугольника DEFH, если AB = 2.

Решение.

а) Пусть P — основание перпендикуляра, опущенного из точки D на прямую AB, тогда DH = DP.

В равнобедренном треугольнике EAD: ∠AED = 30°.

В прямоугольном треугольнике EPD:  откуда получаем, что FH = 2DH.

б) Пусть AM — высота треугольника ABC — пересекает ED в точке N. Тогда

Пусть DH = EF = x, тогда FH = ED = 2x. Треугольники ABC и AED подобны, следовательно

Значит, площадь прямоугольника DEFH равна

 

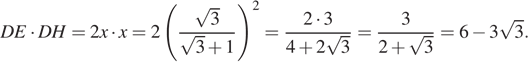
Ответ: 

 

 

 

 

 

 

 

 

12. Задание 16 № 515828

Медианы AA₁, BB₁, и CC₁ треугольника ABC пересекаются в точке M. Точки A₂, B₂ и C₂ — середины отрезков MA, MB и MC соответственно.

а) Докажите, что площадь шестиугольника A₁B₂C₁A₂B₁C₂ вдвое меньше площади треугольника ABC.

б) Найдите сумму квадратов всех сторон этого шестиугольника, если известно, что AB = 5, BC = 8 и AC = 10.

Решение.

а) Площадь треугольника A₁MB₂ в два раза меньше площади треугольника A₁MB, поскольку MB = 2MB₂, а высота, проведённая из вершины A₁, у этих треугольников общая:

Аналогично получаем ещё 5 равенств:     

Складывая эти равенства почленно, получаем

б) Обозначим длины сторон BC, AC, AB треугольника ABC через a, b, c.

Докажем, что квадрат медианы AA₁ равен 

Для доказательства на продолжении отрезка AA₁ за точку A₁ отложим отрезок A₁P = AA₁.Получим параллелограмм ACPB со сторонами AC = PB = b и AB = CP = c и диагоналями BC = a и AP = 2AA₁. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон:  откуда 

Аналогично доказывается, что  а 

Отрезок С₁А₂ — средняя линия треугольника ABM, значит,

Рассуждая аналогично, мы получим, что стороны шестиугольника втрое меньше медиан треугольника ABC:  Следовательно, сумма квадратов сторон шестиугольника равна

 

 

Подставляя в эту формулу длины сторон треугольника ABC, получаем ответ: сумма квадратов сторон шестиугольника равна 

 

Ответ: 

 

13. Задание 16 № 517533

Две окружности касаются внутренним образом в точке A, причем меньшая окружность проходит через через центр O большей. Диаметр BC большей окружности вторично пересекает меньшую окружность в точке M, отличной от A. Лучи AO и AM вторично пересекают большую окружность в точках P и Q соответственно. Точка C лежит на дуге AQ большей окружности, не содержащей точку P.

а) Докажите, что прямые PQ и BC параллельны.

б) Известно, что sinAOC =  Прямые PC и AQ пересекаются в точке K. Найдите отношение QK:KA.

Решение.

а) Так как BC — диаметр, а AQ — хорда, то  AO пересекает большую окружность в P, AP — диаметр, тогда , откуда 

Поскольку  и , то , что и требовалось доказать.

б) Так как  — центральный, то  , значит,  — соответственные углы. Поскольку  — биссектриса , тогда по свойству биссектрисы

 

Ответ: б) 

 

 

 

 

 

 

 

 

 

14. Задание 16 № 503149

Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AKпересекает вторую окружность в точке C.

а) Докажите, что прямые AD и BC параллельны.

б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.

Решение.

Задание а). Обозначим центры окружностей  и  соответственно. Пусть общая касательная, проведённая к окружностям в точке пересекает  в точке  По свойству касательных, проведённых из одной точки,  и.  Треугольник  у которого медиана равна половине стороны, к которой она проведена, — прямоугольный.

Вписанный угол  прямой, поэтому он опирается на диаметр Значит,  Аналогично получаем, что Следовательно, прямые  и  параллельны.

Задание б). Пусть, для определенности, первая окружность имеет радиус 4, а радиус второй равен 1.

Треугольники  и  подобны,  Пусть , тогда 

У треугольников  общая высота, следовательно,  то есть Аналогично,  Площадь трапеции  равна 

Вычислим площадь трапеции  Проведём к  перпендикуляр  равный высоте трапеции, и найдём его из прямоугольного треугольника 

Тогда

Следовательно,  откуда  и 

 

Ответ: 3,2.

 

 

 

 

15. Задание 16 № 514717

На отрезке BD взята точка C. Биссектриса BL равнобедренного треугольника ABC с основанием BCявляется боковой стороной равнобедренного треугольника BLD с основанием BD.

а) Докажите, что треугольник DCL равнобедренный.

б) Известно, что  В каком отношении прямая DL делит сторону AB?

Решение.

а) Обозначим , тогда , , , поэтому  значит, треугольник LCD — равнобедренный.

б) Пусть H — точка пересечения DL с AB. Тогда

поэтому  по двум углам. Отсюда 

Поскольку , то  Пусть BC = x, AB = 3x. По теореме о биссектрисе откуда находим ,  Тогда

значит, , откуда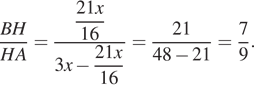 

 

Ответ: 7:9.

 

 

 

 

 

 

16. Задание 16 № 509823

Окружность, построенная на медиане BM равнобедренного треугольника ABC как на диаметре, второй раз пересекает основание BC в точке K.

а) Докажите, что отрезок BK втрое больше отрезка CK.

б) Пусть указанная окружность пересекает сторону AB в точке N. Найдите AB, если BK = 18 и BN = 17.

Решение.

а) Проведём медиану AE к основанию BC, поскольку треугольник ABC — равнобедренный, медиана AE является биссектрисой и высотой. Проведём MK, заметим, что ∠BKM = 90°, так как он вписанный и опирается на диаметр окружности. Поэтому MK перпендикуляр к ВС. Тогда MK — средняя линия AEС, и тогда КС = EК. Поскольку CE = 2CK, имеем: BK = 3CK, что и требовалось доказать.

б) Заметим, что ∠BKM = ∠BNM = 90°, так как эти углы вписанные и опираются на диаметр. Тогда

 (*),

причём:

Подставляя полученные соотношения в (*), получаем:

Тогда 

Ответ: б) 18.

Приведём другое решение пункта б).

Пусть  Тогда   и пусть тогда  По свойству секущих имеем:

 

 

 

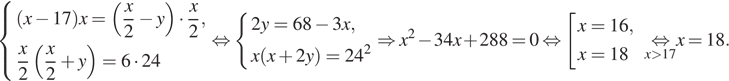
17. Задания Д11 C4 № 507357

Продолжение биссектрисы CD неравнобедренного треугольника ABC пересекает окружность, описанную около этого треугольника, в точке E. Окружность, описанная около треугольника ADE, пересекает прямую AC в точке F, отличной от A. Найдите радиус окружности, описанной около треугольника ABC, если AC = 8, AF = 3, угол BAC равен 45°.

Решение.

Возможны два случая:

1) точка F лежит между A и C (рис. 1);

2) точка A лежит между F и C (рис. 2).

Рассмотрим первый случай.

поэтому треугольники CDF и CDB равны (обща сторона и все углы равны). Значит, BC = FC = AC − AF = 5.

Тогда искомый радиус равен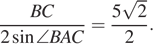 

 

Рассмотрим второй случай.

∠AFD = ∠AED = ∠ABC, поэтому треугольники CDF и CDB равны. Значит, BC = FC = AC + AF = 11. Тогда искомый радиус равен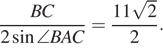 

 

Ответ: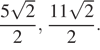 

 

Замечание: на самом деле при внимательном рассмотрении оказывается, что первый случай невозможен, так как оказывается, что 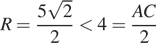 — самой длинной из сторон треугольника, а такого быть не может. Ошибка была допущена составителями задачи. При проверке, полный балл выставлялся, либо в случае, когда были разобраны оба случая и верно получены оба ответа, либо в случае, когда была объяснена невозможность первого случая и дан только один ответ.

 

 

18. Задание 16 № 511403

Дан четырёхугольник 

а) Докажите, что отрезки  и  соединяющие середины его противоположных сторон, делят друг друга пополам.

б) Найдите площадь четырёхугольника , если ,  

Решение.

а) Пусть  и  — середины сторон  и  четырёхугольника соответственно. Тогда  и  — средние линии треугольников  и  Значит,  и  поэтому  — параллелограмм. Его диагонали  и  делят друг друга пополам, что и требовалось доказать.

б) В треугольнике  имеем:

Значит,  Тогда  поэтому треугольник  прямоугольный треугольник с прямым углом при вершине  Четырёхугольник  — прямоугольник, поэтому

Отрезок  является средней линией треугольника  поэтому  Аналогично  Тогда, имеем:

Где  — искомая площадь четырёхугольника  Аналогично Поэтому

Следовательно,

 

Ответ: 

 

 

19. Задания № 486002

Площадь трапеции ABCD равна 810. Диагонали пересекаются в точке O. Отрезки, соединяющие середину P основания AD с вершинами B и C, пересекаются с диагоналями трапеции в точках M и N.Найдите площадь треугольника MON, если одно из оснований трапеции вдвое больше другого.

Решение.

Пусть  (рис. 1). Четырехугольники  и  — параллелограммы, поэтому и  — середины и  значит,  и  — медианы треугольника  Пусть  — высота трапеции. Положим  Тогда

 так как  — точка пересечения медиан треугольника  поэтому

Аналогично,  значит, треугольник  подобен треугольнику  с коэффициентом  Заметим, что поскольку треугольники AOD и BOC подобны с коэффициентом 2, высота треугольника AOD вдвое больше высоты треугольника BOC и составляет две трети высоты трапеции. Имеем:

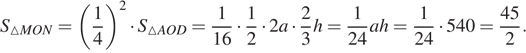
Рассмотрим случай, когда  (рис. 2) Пусть  — высота трапеции. Положим   Тогда, как и в первом случае 

Треугольник  подобен треугольнику  с коэффициентом , а треугольник  – треугольнику  с коэффициентом  Тогда

 

Значит,  Аналогично,  Следовательно,

 

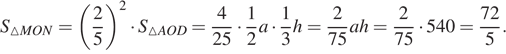
Ответ:  или 

 

 

20. Задания № 503255

Окружность радиуса 6 вписана в угол, равный 60°. Вторая окружность также вписана в этот угол и пересекается с первой в точках M и N . Известно, что расстояние между центрами окружностей равно 4. Найдите MN.

Решение.

Пусть O₁ — центр окружности радиуса 6, O₂ — центр второй окружности, O — вершина угла, в который вписаны окружности, A и B — точки касания соответственно первой и второй окружностей с одной из сторон угла, тогда OO₁ = 2O₁A = 12.

Возможны два случая. Первый случай: точка O₁ лежит между точками O и O₂ (рис. 1), тогда OO₂ = OO₁ + O₁O₂ = 16, откуда радиус второй окружности

В треугольнике O₁MO₂ имеем O₁O₂ = 4, O₁M = 6, O₂M = 8. Поскольку общая хорда MNокружностей перпендикулярна линии центров O₁O₂ и делится ею пополам, высота MH треугольника O₁MO₂ равна половине MN.

В треугольнике O₁MO₂ полупериметр 

откуда

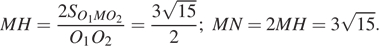
Второй случай: точка O₂ лежит между точками O и O₁ (рис. 2), тогда OO₂ = OO₁ − O₁O₂ = 8, откуда радиус второй окружности

Аналогично первому случаю, в треугольнике O₁MO₂ имеем O₁O₂ = 4, O₁M = 6, O₂M = 4, высота MH треугольника O₁MO₂ равна половине MN.

В треугольнике O₁MO₂ полупериметр 

откуда

 Ответ:  или 

21. Задания  № 507179

В треугольнике  Точка D лежит на прямой BC причем  Окружности, вписанные в каждый из треугольников ADC и ADB касаются стороны AD в точках E и F. Найдите длину отрезка EF.

Решение.

Пусть , ,  Используя свойства касательных, подсчитаем разными способами периметры треугольников

Откуда получаем:  Аналогично, 

Тогда 

Возможны два случая:

1. Точка  лежит на отрезке  Тогда  значит, 

 

2. Точка D лежит вне отрезка  Тогда  значит, 

Ответ: 3 или 6.

 

 

 

 

 

 

 

 

 

 

 

 

22. Задания № 507598

Окружность, вписанная в треугольник ABC, площадь которого равна 114, касается средней линии, параллельной стороне BC. Известно, что BC = 19. Найдите сторону AB.

Решение.

Обозначим AB = x, AC = y, p — полупериметр треугольника ABC. Пусть M и N — середины сторон AB и AC соответственно. Тогда 

В трапецию BMNC вписана окружность поэтому

Значит,

По формуле Герона

Отсюда находим, что x = 20 или x = 37.

 

 

 

 

 

 

 

 

 

 

 

 

23. Задания № 484624

Прямая, перпендикулярная боковой стороне равнобедренного треугольника, отсекает от него четырёхугольник, в который можно вписать окружность. Найдите радиус окружности, если отрезок прямой, заключённый внутри треугольника, равен 6, а отношение боковой стороны треугольника к его основанию равно 

Решение.

Обозначим данный треугольник ABC, BC = 6x — основание, AB = AC = 5x. Заметим, что окружность, о которой говорится в условии, — окружность, вписанная в треугольник ABC. Пусть O — её центр, а E — точка касания с основанием BC.

Обозначим 

Так как BO — биссектриса треугольника ABE, то следовательно, 

Первый случай. Пусть прямая MN перпендикулярная AB, касается окружности, пересекает AB в точке M, а AC в точке N (рис. 1). Тогда , 

В треугольнике AMN, имеем 

У описанного четырехугольника суммы противоположных сторон равны:

откуда находим: 

Второй случай. Пусть прямая MN перпендикулярная AB, касается окружности, пересекает AB в точке M, а BC в точке N (рис. 2). В прямоугольном треугольнике BMN имеем 

У описанного четырёхугольника ACNM суммы противоположных сторон равны:

, 

откуда находим: 

Ответ:  или 

 

24. Задания Д11 C4 № 514640

На катетах AC и BC прямоугольного треугольника ABC как на диаметрах построены окружности, второй раз пересекающиеся в точке M. Точка Q лежит на меньшей дуге MC окружности с диаметром BC. Прямая CQ второй раз пересекает окружность с диаметром AC в точке P.

а) Докажите, что прямые PM и QM перпендикулярны.

б) Найдите PQ, если AM = 6, BM = 2, а Q — середина дуги MC.

Решение.

а) Поскольку  точки M, A и B лежат на одной прямой, значит, отрезок CM — высота треугольника ABC (см. рисунок).

Четырёхугольники AMPC и BQMC вписаны в окружности, поэтому

откуда 

б) Из прямоугольного треугольника ABC получаем:  откуда  

Точка Q — середина дуги MC, поэтому BQ — биссектриса угла CBM. Значит,

Получаем:   как хорды, стягивающие равные дуги. Таким образом, 

Ответ: б) 4.

 

 

 

 

 

 

 

 

 

25. Задания Д11 C4 № 502025

Угол C треугольника ABC равен 30°, D — отличная от A точка пересечения окружностей, построенных на сторонах AB и AC как на диаметрах. Известно, что BD:DC = 1:3. Найдите синус угла A.

Решение.

Пусть BD = x, тогда по условию DC = 3x. Поскольку D — точка пересечения окружностей, построенных на сторонах AB и AC как на диаметрах, ∠ADB = ∠ADC = 90°, значит, точки B, C и D лежат на одной прямой.

В прямоугольном треугольнике ACD угол ∠C = 30°, откуда  В прямоугольном треугольнике ABD 

Возможны два случая. Первый случай: угол ABC тупой (рис. 1), тогда точка B лежит между точками D и C, значит, BC = DC − BD = 2x. В треугольнике ABC имеемAB = BC = 2x, значит, он равнобедренный с основанием AC, следовательно, ∠A = ∠C = 30°, откуда  

Второй случай: угол ABC острый (рис. 2), тогда точка D лежит между точками B и C, значит, BC = DC + BD = 4x. 

По теореме синусов для треугольника ABC:

 откуда 

Ответ:  или 1.

 

 

 

 

 

 

 

 

 

 

 

 

26. Задания Д11 C4 № 511332

Боковые стороны AB и CD трапеции ABCD равны 9 и 12 соответственно. Отрезок, соединяющий середины диагоналей, равен 7,5, средняя линия трапеции равна 37,5. Прямые AB и CD пересекаются в точке М. Найдите радиус окружности, вписанной в треугольник ВМС.

Решение.

В любой трапеции отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований трапеции, а средняя линия — полусумме оснований трапеции. В нашем случае полуразность оснований равна 7,5, а полусумма оснований равна 37,5, поэтому основания трапеции равны 30 и 45.

Предположим что  (рис. 1). Стороны BС и АD треугольников МВС и MADпараллельны, поэтому эти треугольники подобны с коэффициентом  Значит,

, 

Заметим, что , поэтому треугольник МВС — прямоугольный с гипотенузой BС. Радиус его вписанной окружности равен: 

 Пусть теперь ,  (рис. 2). Аналогично предыдущему случаю можно показать, что радиус вписанной окружности треугольника MAD равен 9. Треугольник MAD и МВСподобны с коэффициентом  Значит, радиус вписанной окружности треугольника МВС равен 

Ответ: 6; 9.

 

 

 

 

 

 

 

 

 

 

27. Задания Д11 C4 № 511299

В треугольнике  Точка D лежит на прямой BC причем  Окружности, вписанные в каждый из треугольников ADC и ADB касаются стороны AD в точках E и F. Найдите длину отрезка EF.

Решение.

Пусть , ,  Используя свойства касательных, подсчитаем разными способами периметры треугольников

Откуда получаем:  Аналогично, 

Тогда 

Возможны два случая:

1. Точка  лежит на отрезке  Тогда  значит, 

 

2. Точка D лежит вне отрезка  Тогда  значит, 

 

Ответ:  или 

 

 

 

 

 

 

 

 

 

 

28. Задание 14 № 504853

Дан равнобедренный треугольник ABC с основанием AC. Вписанная в него окружность с центром O касается боковой стороны BC в точке P и пересекает биссектрису угла B в точке Q.

а) Докажите, что отрезки PQ и OC параллельны.

б) Найдите площадь треугольника OBC, если точка O делит высоту BD треугольника в отношении BO : OD = 3 : 1 и AC = 2m.

Решение.

Пусть отрезок BD — высота данного треугольника. Тогда O ∈ BDв силу того, что ABC — равнобедренный треугольник. Введем следующие обозначения: ∠BCO = ∠DCO = α, ∠COP = x, ∠OPQ = y, Прямоугольные треугольники BOP и BCD подобны, следовательно ∠BOP = 2α. Из прямоугольного треугольника OPC находим  а из равнобедренного треугольника OPQ находим  Углы COP и OPQ ― накрест лежащие при пересечении прямых PQ и OC секущей OP, значит, отрезки PQ и OC параллельны, что и требовалось доказать.

б) Отрезок CO ― биссектриса треугольника BCD, следовательно:

Откуда BC = 3DC = 3m.

CP = DC = m, значит, BP = 2m и, следовательно:

Откуда  По формуле Герона находим:

откуда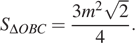 

 Ответ: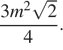 

29. Задания № 501458

Расстояние между параллельными прямыми равно  На одной из них лежит вершина , на другой — основание  равнобедренного треугольника  Известно, что  Найдите расстояние между центрами окружностей, одна из которых вписана в треугольник , а вторая касается данных параллельных прямых и боковой стороны треугольника 

Решение.

Пусть  — высота треугольника ,  и  — радиус и центр вписанной окружности, , , поэтому  Найдем площадь, полу периметр и радиус вписанной окружности треугольника :

 

Тогда  Кроме того, по теореме Пифагора

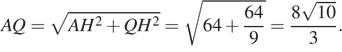
Пусть окружность с центром в точке  касается боковой стороны  равнобедренного треугольника  и данных параллельных прямых. Радиус этой окружности равен , поскольку он вдвое меньше расстояния между прямыми. Точку касания окружности с прямой  обозначим 

Пусть точки  и  лежат по разные стороны от точки  (рис. 1). Центр окружности, вписанной в угол, лежит на его биссектрисе, поэтому  и  — биссектрисы смежных углов  и соответственно. Значит,  и  поскольку эти углы образованы парами соответственно перпендикулярных прямых. Следовательно, прямоугольные треугольники  и  подобны с коэффициентом  Поэтому

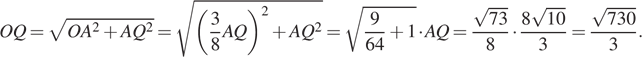
Пусть точки  и  лежат по одну сторону от точки  (рис. 2). Центр окружности, вписанной в угол, лежит на его биссектрисе, поэтому лучи  и  совпадают и являются биссектрисой угла  Значит, прямоугольные треугольники  и  подобны с коэффициентом  Тогда

Ответ: 

30. Задания № 514515

Точки A₁, B₁ и C₁ — середины сторон соответственно BC, AC и AB треугольника ABC, в котором угол A тупой.

а) Докажите, что отличная от A₁ точка пересечения окружностей, описанных около треугольников A₁CB₁ и A₁BC₁, лежат на окружности, описанной около треугольника B₁AC₁.

б) Известно, что AB = AC = 13 и BC = 24. Найдите радиус окружности, вписанной в треугольник, вершинами которого являются центры окружностей, описанных около треугольников A₁CB₁, A₁BC₁ и B₁AC₁.

Решение.

а) Пусть O — отличная от A₁ точка пересечения окружностей, описанных около треугольников A₁CB₁ и A₁BC₁ (рис. 1).

Тогда

откуда 

Значит,  следовательно, точки A, B₁, O и C₁ лежат на одной окружности.

б) Пусть O₁, O₂ и O₃ — центры окружностей, описанных около треугольников B₁AC₁, A₁BC₁ и A₁CB₁ соответственно (рис. 2). Заметим, что  как радиусы описанных окружностей около равных треугольников. Значит, треугольники AO₁C₁ и C₁O₂B равны. Кроме того, треугольник O₂C₁O₁ также равен этим треугольникам, поскольку

Таким образом,  Аналогично,   поэтому треугольник O₁O₂O₃ подобен треугольнику ABC с коэффициентом  и радиус вписанной в него окружности равен половине радиуса окружности, вписанной в треугольник ABC.

Пусть M — середина BC, а радиус окружности, вписанной в треугольник ABC, равен r (рис. 3). Тогда площадь треугольника ABC равна

C другой стороны, высота равнобедренного треугольника ABC равна  поэтому площадь треугольника ABC равна 60. Значит, r = 2,4. Искомый радиус равен  Ответ: 1,2.

31. Задания № 511425

Две окружности пересекаются в точках A и B. Через точку A проведены диаметры AC и AD этих окружностей. Найдите расстояние между центрами окружностей, если BC = 8, BD = 4.

Решение.

Пусть центры окружностей  и  Ясно, что  — средняя линия треугольника Проведём отрезок  Углы  и  — вписанные, и каждый из них опирается на диаметр соответствующей окружности. Следовательно,  Таким образом, точки  и  лежат на одной прямой. Возможны два случая: точки  и  лежат по разные стороны от точки  или по одну сторону от точки  (см. рис.).

В первом случае  Во втором случае 

Ответ: 6 или 2.

 

 

 

 

Задача 1 (медианы в треугольнике).

Медианы АМ и BN треугольника АВС перпендикулярны и пересекаются в точке Р.

а) Докажите, что СР=АВ.

б) Найдите S _ΔАВС, если известно, что АС=6 и ВС=7.

Повторить. 1) медианы треугольника пересекаются в одной точке и точкой пересечения делятся в отношении 2:1; 2) медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине; 3) каждая медиана делит треугольник на два, равных по площади.

Решение

1)      Так как медианы треугольника пересекаются в одной точке, то СР – это отрезок медианы. Пусть СР пересекается с АВ в точке К, тогда СК – медиана треугольника и  СР= СК=2РК (свойство медиан)

2)      РК – медиана прямоугольного треугольника АВР, поэтому РК=0,5АВ.

3)      Из 1) и 2)=>АВ=2PK =СР.

Пункт а) доказан.

б) 1) Пусть ВР=2х, PN=х, АР=2у, РМ=у. Применяя теорему Пифагора для треугольников ВМР и АРN, получим систему

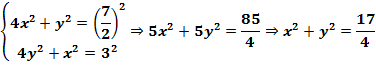
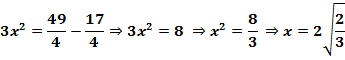
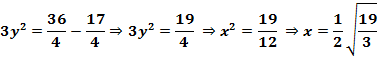
2) АМ – медиана треугольника АВC, поэтому площадь треугольника АВМ  равна

 

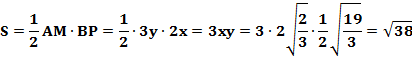
Значит, площадь треугольника АВС равна  

Ответ: S _ΔАВС =

 

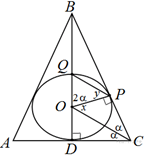
Задача 2 (метод площадей).

Окружность с центром О, вписанная в S _ΔАВС касается стороны ВС в точке Р и пересекает отрезок ВО в точке Q. Отрезки OC II QP

а) Доказать: S _ΔАВС – равнобедренный

б) Найти  S _ΔBPQ, если точка О делит высоту ВН в отношении ВО: ОН=3:1,  АС =2а.

Повторить.   Для  доказательства пункта a) необходимо вcпомнить признаки равнобедренного треугольника:  если высота и биссектриса, проведенная к одной стороне, совпадают, то такой треугольник является равнобедренным.

Решение

 

а) 1)  ΔАВС – описанный около окружности, поэтому  О – точка пересечения биссектрис.

 

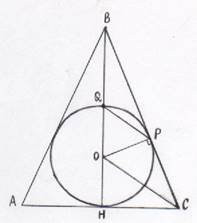
2)   OPBC (радиус, проведенный в точку касания), значит  ΔВРО – прямоугольный.

3) Пусть углы АСО и ВСО равны α, тогда угол СОР равен 90-α и равен углу ОРQ, так как ОС II QP, углы OPQ и COP – накрест лежащие.

 ΔQOP  - равнобедренный, так как OQ=OP (радиусы).
QOP =-2

4)  Пусть ВО пересекается с АС в точке Н. Рассмотрим треугольники ВОР и ВСН. У них угол при вершине В общий,  ВОР=ВСН=2α. Значит, ΔВОР подобен ΔВСН по двум углам. Следовательно,  ВНС=ВРО=90°

5) Рассмотрим треугольник АВС. У него ВН является биссектрисой и высотой. Поэтому по признаку равнобедренного треугольника ΔАВС – равнобедренный. Пункт а) доказан.

б) При нахождении S _ΔBQP будем использовать «метод площадей»: если два треугольника имеют общий угол, то их площади относятся как произведения сторон, содержащих этот угол, то есть  если     = k и = m, то = km.

1) ΔАВС – равнобедренный (см. пункт а),  ВН – высота, => ВН – медиана. Если АС = 2а по условию, то НС = а.

2) НС = СР = а (свойство отрезков касательных)

3) СО – биссектриса ΔВНС. По свойству биссектрисы треугольника   =  = 3:1(по условию). Поэтому ВС=3а, тогда ВР = ВС – РС = 3а - а = 2а. С другой стороны  = 3,   

S _ΔBHC=0,5∙ ВН∙ НС =0,5∙ НС=0,5 ∙а = а²

4)  BQ : BH=1 : 2; BP : BC=2 : 3. Поэтому S_BQP = 0,5 ∙  = .

Задача в пункте б) может быть решена другими способами. Например, ΔОНС и ΔВНС имеют общую высоту  HС.   = .  S_OPC = S_OHC. Поэтому S_BPO=0,5 S _BHC. Аналогично, S_BQP =  S_BPO. Значит, S_BQP =

Возможно и третье решение. Из треугольника ВНС найти синус угла НВС, далее, вычислив стороны BQ и BP треугольника BQP, найти его площадь

S_{BQP =} 

Ответ:

 

Задача 3 (вписанный четырехугольник).

На гипотенузу АВ прямоугольного ΔАВС опустили высоту СН. Из точки Н на катеты опустили перпендикуляры НК и НЕ

 а) Доказать, что точки А, В, К и Е лежат на одной окружности,

 б) Найти радиус этой окружности, если АВ=12, СН=5.

Повторить. Свойство вписанного четырехугольника: сумма противоположных углов равна 180°, справедливо и обратное.

Решение

    

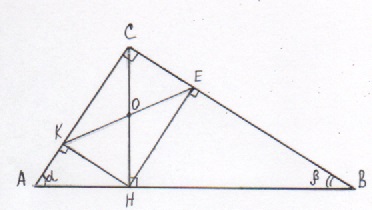
а)  Если точки А, В, К и Е лежат на одной окружности, то четырехугольник АВКЕ – вписанный.

 1) Пусть угол  А равен α, угол В равен β, тогда α+β=90°. Используя свойство прямоугольного треугольника (сумма острых углов равна 90°) и далее в ΔАСН, ΔКСН, ΔСНВ и ΔСНЕ, получим  

2) Четырехугольник КСЕН – прямоугольник, поэтому его диагонали равны и точкой пересечения делятся пополам. Значит, ΔОНЕ и ΔОНК равнобедренные ∠ОКН=∠ОНК=α, ∠ОНЕ=∠ОЕН=β  (как углы при основании).

3) В четырехугольнике АКЕВ: ∠А+∠КЕВ=α+90°+β=180°, ∠B+∠АКЕ= α+90°+β=180°. Значит, около АКЕВ можно описать окружность. Пункт а) доказан.

б) 1) Нарисуем окружность. Проведем АR перпендикулярно АВ, точка R принадлежит окружности. Угол RAB равен 90° - вписанный, поэтому опирается на диаметр окружности RB.

                                                                      

Угол НЕВ равен 90°, поэтому точки R, H и Е лежат на одной прямой

2) АСHR – параллелограмм, противоположные стороны его равны. AR=CH=5

3) По теореме Пифагора из ΔARB получим, что BR===13. Значит R_окр=0,5 ВК=6,5

Другой способ нахождения радиуса окружности: из ΔАСВ найти угол α, его катеты и АЕ. В ΔАКЕ  ∠АКЕ=90°+α.  Треугольник АКЕ вписанный в данную окружность. По следствию из теоремы синусов =2R

 Ответ: 6,5.

 

 

 

Задача 4 (описанный четырехугольник).

В равнобедренную трапецию АВСD с основаниями AD и ВС вписана окружность, СН – высота трапеции.

 а) Доказать, что центр окружности, вписанной в трапецию, лежит на отрезке ВН.

K

 б) Найдите диагональ АС, если известно, что средняя линия трапеции равна , а угол AOD равен 135°, где О – центр окружности, вписанной в трапецию, AD – большее основание.

Решение.

 

                                                                         

а) 1) Пусть точки K и L – точки касания окружности оснований трапеции, тогда

 ОК = ОL = r_впис

   2) ΔBOK=ΔHOL по катету(см. пункт 1) и острому углу  (углы  OBK и LHO равны как накрест лежащие при BC II AD и секущей BH. Поэтому ВО = ОН.

   3) Центр вписанной в трапецию окружности лежит на пересечении биссектрис внутренних углов трапеции. Данная трапеция ABCD – равнобедренная, поэтому углы ОВК и ОСК равны. Значит, треугольники ΔВОК и ΔСОК равны (по катету и острому углу)

   4) Из 2) и 3) следует, что ВО=ОС=ОН. Точка О равноудалена от вершин прямоугольного треугольника  ΔВСН. О – центр описанной около треугольника окружности. Следовательно О принадлежит ВН (его середина). Пункт а) доказан.

 

 

 

 б) Для доказательства пункта б) сделаем дополнительный чертеж

                            

1)      Пусть MN – средняя линия трапеции. Точка О принадлежит MN и О – её середина, поэтому МО =

2)      АО – биссектриса, углы МАО и RAO равны, углы RAO и МОА раны как накрест лежащие. ΔАМО – равнобедренный, АМ=МО=. Тогда АВ = 2АМ=

3)      ∠AOD=135° (по условию), ∠OAD+∠ODA=45°.  Значит,  ∠BAD=∠CDA=45°. Пусть BR перпендикулярен AD.  BR = AR=

4)      Пусть CD₁ II BD и точка D₁ лежит на прямой AD. Четырехугольник ВСD₁D – параллелограмм. CD₁=BD (противоположные стороны),  BD=AC(диагонали равнобедренной трапеции). Тогда СD₁=BD=AC.

5)   ₁ – равнобедренный, AD₁ – основание. АD₁=AD+DD₁=AD+BC=2MN=2. CH=BR=. По теореме Пифагора из ΔCHА: AC==²= = 3

Ответ: АС = 3.

 

 

 

Задача 5

В треугольнике АВС угол ВАС равен 60^°, угол АВС равен 45^°. Продолжения высот треугольника АВС пересекают описанную около него окружность в точках M, N, P.

а) Докажите, что треугольник MNP прямоугольный.

б) Найдите площадь треугольника MNP, если ВС=12.

Повторить.  Свойство вписанных углов; теорему синусов.

Решение.

а) Пусть продолжения высот треугольника АВС, проведенных из вершин А, В и С, пересекают описанную около него окружность в точках M, N и  P соответственно.

Тогда вписанные углы PNB  и  PCB опираются на одну и ту же дугу, поэтому 

Аналогично,  

Значит,

 

Следовательно, треугольник MNP прямоугольный. Пункт а) доказан.

б) Угол MNA равен углу NBA , угол APM равен углу ACP  (вписанные углы, опирающиеся на одну дугу). 

Тогда
  

Следовательно,  = 30^°. 

Пусть R – радиус описанной окружности треугольника АВС. По теореме синусов

 

Тогда

=

 

Следовательно,

Ответ:

 

 

 

 

 

 

 

 

 

 

 

 

 

Скачано с www.znanio.ru