Добавить материал

и получить 10 документов
и свидетельство СМИ

Кривцова Светлана Александровна

Сборник "Решение тригонометрических уравнений"

doc
01.06.2020

Публикация в СМИ для учителей

Бесплатное участие. Свидетельство СМИ сразу.
Мгновенные 10 документов в портфолио.

Добавить материал

Сборник содержит материал для подготовке к ЕГЭ по математике (профильный уровень)

сборник Решение тригонометрических уравнений.doc

МБОУ «Лицей города Абдулино»

Методические аспекты подготовки учащихся

к решению тригонометрических уравнений (Задание №13)

учитель математики: Кривцова Светлана Александровна

г. Абдулино 2020г.

Оглавление

1. Критерии оценивания выполнения задания №13	3
2. Основные формулы тригонометрии	3
3. Классификация методов решения тригонометрических уравнений	5
4. Восемь способов решения одного уравнения	8
5. Способы отбора корней в тригонометрических уравнениях	14
6. Решение тригонометрических уравнений из материалов ЕГЭ	17

Критерии оценивания выполнения задания №13

Содержание критерия	Баллы
Обосновано получены верные ответы в обеих пунктах	2
Обоснованно получен верный ответ в пункте а или пункте б, или получен ответ неверный из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов – пункта а и пункта б	1
Решение не соответствует ни одному из критериев, перечисленных выше	0
Максимальный балл	2

Основные формулы тригонометрии

1) основное тригонометрическое тождество sin²α +cos² α= 1,

Деля это уравнение на квадрат косинуса и синуса, соответственно имеем

2) формулы двойного аргумента sin2α =2 sinα cos α,

cos 2α = cos² α - sin²α,

cos 2α = 1- 2sin²α,

3) формулы понижения степени: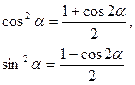

4) формулы суммы и разности двух аргументов:

sin(α+β)=sinα cos β +cos α sin β

sin(α-β)=sinα cos β -cos α sin β

cos(α+β)=cosα cos β +sin α sin β

cos(α-β)=sinα cos β +sinα sin β

5)Формулы приведения

Формулами приведения называются формулы следующего вида:

$f ( n \pi + \alpha ) = \pm f (\alpha),\,$

$f ( n \pi - \alpha ) = \pm f (\alpha),\,$

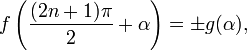
$f \left( \frac{(2n+1) \pi}{2} + \alpha\right) = \pm g (\alpha),\,$

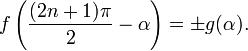
$f \left( \frac{(2n+1) \pi}{2} - \alpha\right) = \pm g (\alpha).\,$

6) Суммы суммы и разности тригонометрических уравнений

$\sin \alpha \pm \sin \beta = 2 \sin \frac{\alpha \pm \beta}{2} \cos \frac{\alpha \mp \beta}{2}$

$\cos \alpha + \cos \beta = 2 \cos \frac{\alpha+\beta}{2} \cos \frac{\alpha-\beta}{2}$

$\cos \alpha - \cos \beta = - 2 \sin \frac{\alpha+\beta}{2} \sin \frac{\alpha-\beta}{2}$

$\operatorname{tg} \alpha \pm \operatorname{tg} \beta = \frac{\sin (\alpha \pm \beta)}{\cos \alpha \cos \beta}$

$1 \pm \sin {2 \alpha} = (\sin \alpha \pm \cos \alpha)^2 .$

6) Чётность

Косинус— чётная, синус, тангенс и котангенс— нечётные, то есть:

$\sin \left( - \alpha \right) = - \sin \alpha \,,$

$\cos \left( - \alpha \right) = \cos \alpha \,,$

$\mathop{\mathrm{tg}}\, \left( - \alpha \right) = - \mathop{\mathrm{tg}}\, \alpha \,,$

$\mathop{\mathrm{ctg}}\, \left( - \alpha \right) = - \mathop{\mathrm{ctg}}\, \alpha \,,$

7) Непрерывность

Синус и косинус — непрерывные функции. Тангенс и имеет точки разрыва ,котангенс 0; ±π; ±2π;…

8) Периодичность

Функции y = cos x, y = sin x — периодические с периодом 2π,

функции y = tg x и y = ctg x — c периодом π.

9) Знаки тригонометрических функций по четвертям

10)Таблица значений тригонометрических функций некоторых углов

Определение. Уравнения, в которых переменная стоит под знаком тригонометрической функции, называются тригонометрическими.

Типы тригонометрических уравнений

ü Простейшие

ü Сложные:

уравнения, сводимые к алгебраическим
однородные уравнения
уравнения, решаемые разложением на множители
применение условия равенства одноименных тригонометрических функций
применение формул сложения тригонометрических функций и формул сложения углов и разложения произведения тригонометрических функций в сумму
уравнения, решаемые с помощью формул понижения степени
уравнения вида a sin x+b cos x= c

Классификация методов решения тригонометрических уравнений

Решение простейших тригонометрических уравнений можно свести в легко запоминающуюся таблицу:


нет решения	,	,	,	,
нет решения	,	,	,	,
a – любое
		,	,	,
		,	,	,

	Методы	Суть метода
1.	Разложение на множители	а) путём вынесения общего множителя за скобки б) с помощью формул сокращённого умножения в) разложение на множители квадратного трёхчлена г) способом группировки и т.д.
2.	Введение новой переменной	а) сведение к квадратному уравнению	Путём введения новой переменной уравнение сводится к квадратному уравнению
		б) универсальная подстановка	; (, т.е. , ) после подстановки получается рациональное уравнение относительно вспомогательного неизвестного
		в) введение вспомогательного аргумента	Часть уравнения приводится к виду , где .
3.	Сведение к одному уравнению	Использование тождества .
4.	Тождественные преобразования в решении стандартных тригонометрических уравнений	Решение уравнения представляет собой цепочку тождественных преобразований. Целью этих преобразований является сведение тригонометрического уравнения к хорошо известному виду уравнению алгебраического, а далее к нескольким элементарным тригонометрическим уравнениям. Пример: . Решение: применив формулу преобразования произведения в сумму, получим , . Применим формулу преобразования разности синусов в произведение имеем: , или , получим ответ: ; .
5.	Решение тригонометрических уравнений возведением обеих частей уравнения в квадрат	Пример: . Возведя обе части в квадрат и применив формулу имеем , , или . Так как при возведении в квадрат возможно появление посторонних корней, то необходима проверка получения корней , , , . Ответ: , , , .
6.	Методы искусственных преобразований	1) Умножение обеих частей на одну и ту же тригонометрическую функцию. Пример: . Раскроем скобки и преобразуем произведение в сумму: , . Умножим обе части уравнения на ( не является решением уравнения). . Преобразуем произведения в суммы: ; ; ; . Исключим из найденных серий корни вида , ; , ; . Ответ: , ; , ; , , , . 2) Прибавление к обеим частям одного и того же числа, одной и той же тригонометрической функции. 3) Тождественное преобразование одной из частей уравнения. 4) Использование свойств пропорции. 5) Тождественное преобразование одной из частей уравнения.
7.	Использование свойств функций, входящих в уравнения:
	а) обращение к условию равенства одноименных тригонометрических функций;
	б) использование свойства ограниченности функций	Если функции и таковы, что дл всех x выполняются неравенства и , и дано уравнение , то оно равносильно системе
	в) условие монотонности функций, входящих в уравнение	Если данное уравнение имеет в одной части функцию монотонную на J, а в другой – постоянную, то такое уравнение не может иметь более одного корня на J. Если одна часть уравнения представляет собой возрастающую, а другая – убывающую функцию, то графики таких функций не могут иметь более одной общей точки, следовательно, уравнение не может иметь более одного корня.
	г) наибольшее и наименьшее значения функции	Если функция и в точке принимает свое наибольшее (наименьшее) значение, а достигает наименьшего (наибольшего) значения, то - единственное решение.

4. Восемь способов решения одного уравнения

1. Используя формулы половинного угла:

;

; или разделим на ;

, ; ;

, . , ;

, .

Ответ: , ; , .

2. Используя формулы приведения:

; из суммы делаем произведение

;

, ;

, ; , ;

, . , .

Ответ: , ; , .

3.Приведение к однородному квадратному уравнению:

;

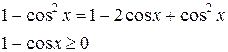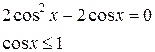; (верно при любых )

;

; или ;

; , .

, .

Оба корня удовлетворяют ОДЗ.

Ответ: , ; , .

4. Введение вспомогательного угла:

;

, ;

если , то

, ;

если , то

, ;

, .

5. разделим на :

;

, ;

, или , .

Ответ: , ; , .

6. Используя формулы понижение степени:

;

Проверка ОДЗ: ;

;

Возведем уравнение в квадрат:

, умножим на 2;

;

; или ;

, ; , ;

, ; , .

Если -нечетное, , то ;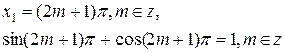

-1=1 – неверно .

Если -нечетное, , то ;

;

-1=1 – неверно.

Если k – чётное, , то ,

следовательно ,

1=1 верно

если n – чётное, ,то ,

следовательно ,

1=1 верно.

Ответ: , ; , .

7. Используя универсальные подстановки:

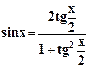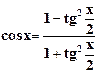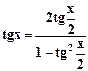; ; , при .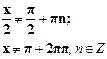

Применение этой подстановки требует большой осторожности! Следует проверить, а не является ли серия корней , корнями данного уравнения (иначе будет потеря корней). Это делается путем подстановки в первоначальное уравнение.

;

Если , , то ;

;

– неверно.

Следовательно , не является корнем уравнения.

Выполним подстановку:

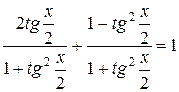, пусть ;

;

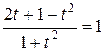; или ;

; ;

, ; , ;

, . , .

Ответ: , ; , .

Решим уравнение возведением в квадрат:

Надо быть аккуратными – могут появиться лишние корни.

;

, ;

, .

Проверка корней:

Если ; ;

;

1=1 – верно;

; ;

;

1=1 – верно;

; ;

;

-1=1 – неверно;

; ;

-1=1 – неверно;

Ответ: , ; , .

Проблемы, возникающие при решении тригонометрических уравнений

1.Потеря корней:

ü делим на g(х).

ü опасные формулы (универсальная подстановка).

Этими операциями мы сужаем область определения.

2. Лишние корни:

ü возводим в четную степень.

ü умножаем на g(х) (избавляемся от знаменателя).

Этими операциями мы расширяем область определения.

5. Способы отбора корней в тригонометрических уравнениях

1.Арифметический (непосредственная подстановка корней в уравнение и имеющиеся ограничения)

2.Алгебраический (решение неравенства относительно неизвестного целочисленного параметра и вычисления корней)

3. Геометрический способ

ü отбор корней тригонометрического уравнения на числовой окружности

ü отбор корней тригонометрического уравнения на числовой прямой

4.Функционально-графический способ

Пример.

а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку

Решение.

а)

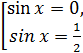
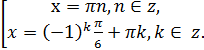
Ответ:

Отбор корней по единичной окружности.

Корни уравненияизображаются точками А и В, а корни уравнения - точками C и D, промежуток изображен жирной дугой (см. рис.).

В указанном промежутке содержатся три корня уравнения: и .
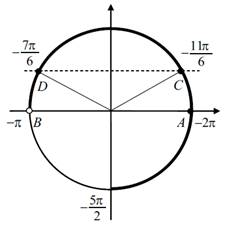
1125682_html_19ffcad1
б) Ответ:

2. Отбор корней по графику.

б) Корни, принадлежащие промежутку , отберем по графику y = sin x. Прямая y = 0 (ось Ox) пересекает график в единственной точке абсцисса которой принадлежит промежутку .

Прямая пересекает график ровно в двух точках, абсциссы которых принадлежат (см. рис.). Так как период функции y = sin x равен , то эти абсциссы равны, соответственно, и .
1125682_html_m13026e1f
В промежутке содержатся три корня:

б) Ответ:

3. Отбор корней перебором значений.

б) Пусть

При n = 0 получаем Ï

При n = 1 получаем Ï

При n = 2 получаем

При n = 3 получаем Ï

Пусть

При k = 0 получаем Ï

При k = получаем

При k = получаем Ï

Промежутку принадлежат корни:

б) Ответ:

4. Отбор корней аналитически с помощью неравенств.

б) Отберем корни, принадлежащие промежутку
Пусть

Тогда

Корень, принадлежащий промежутку : .

Пусть

Тогда

Корень, принадлежащий промежутку : .

Пусть

Тогда

Корень, принадлежащий промежутку :

Промежутку принадлежат корни:

б) Ответ:

6. Решение тригонометрических уравнений из материалов ЕГЭ

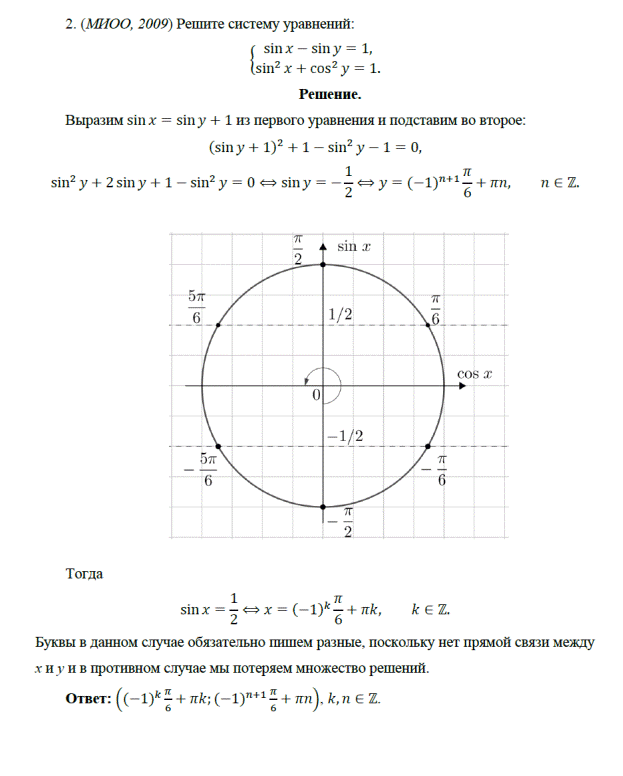
4. (МИОО, 2010) Решите систему уравнений:

5. (МИОО, 2010) Решите систему уравнений:

6. (МИОО, 2010) Решите систему уравнений:

7. (МИОО, 2010) Решите систему уравнений:

8. (МИОО, 2010) Решите уравнение:

(МИОО, 2010) Решите уравнение:

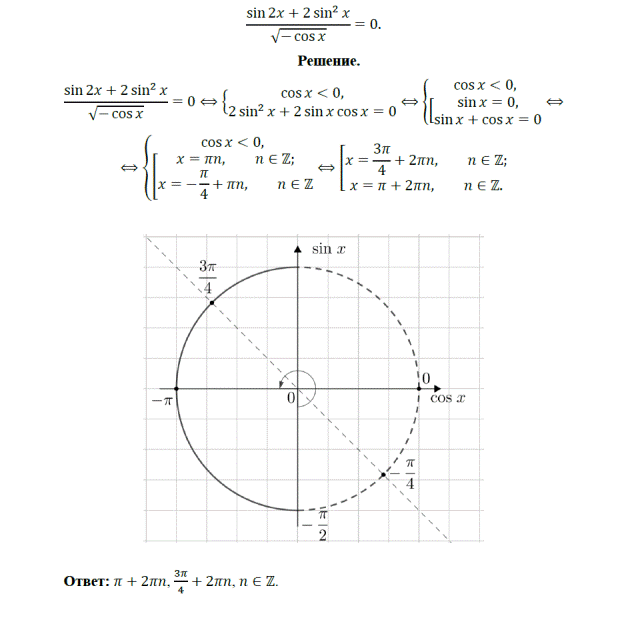
10. (МИОО, 2011) Решите уравнение:

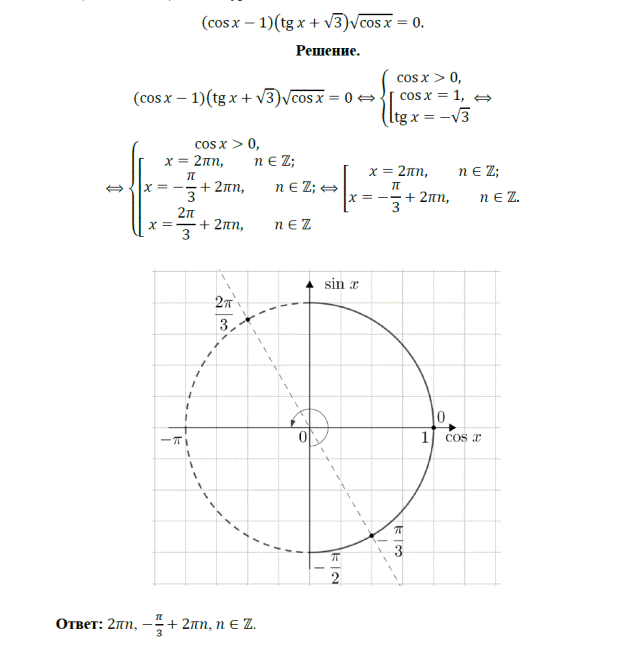
11. (МИОО, 2011) Решите уравнение:

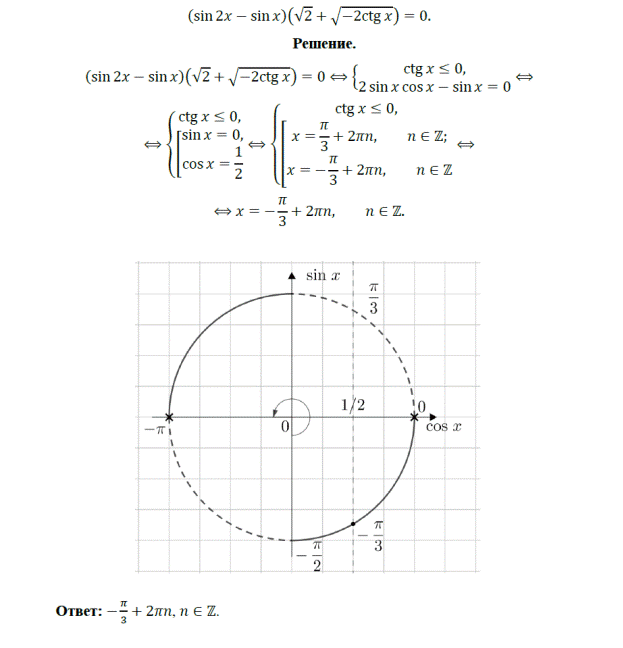
12. (МИОО, 2011) Решите уравнение:

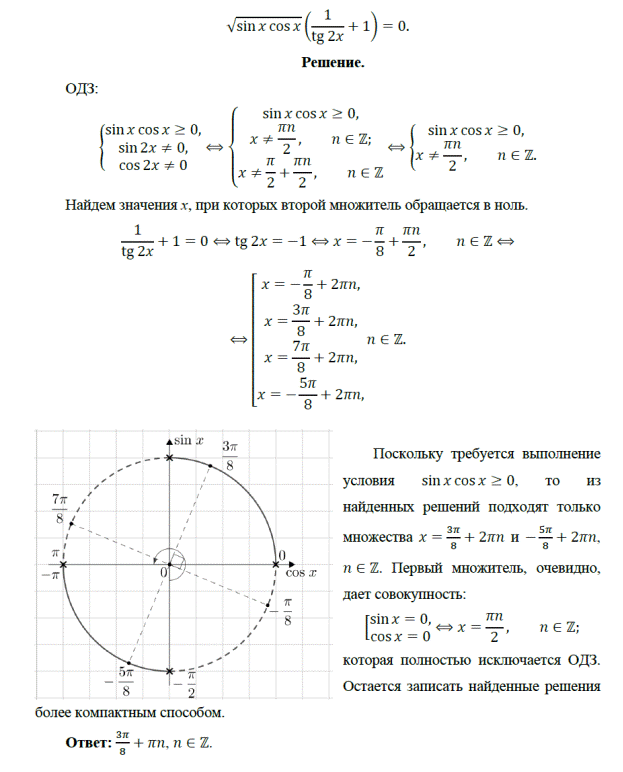
13. (МИОО, 2011) Решите уравнение:

14. (Репетиционный ЕГЭ, 2011) Решите уравнение:

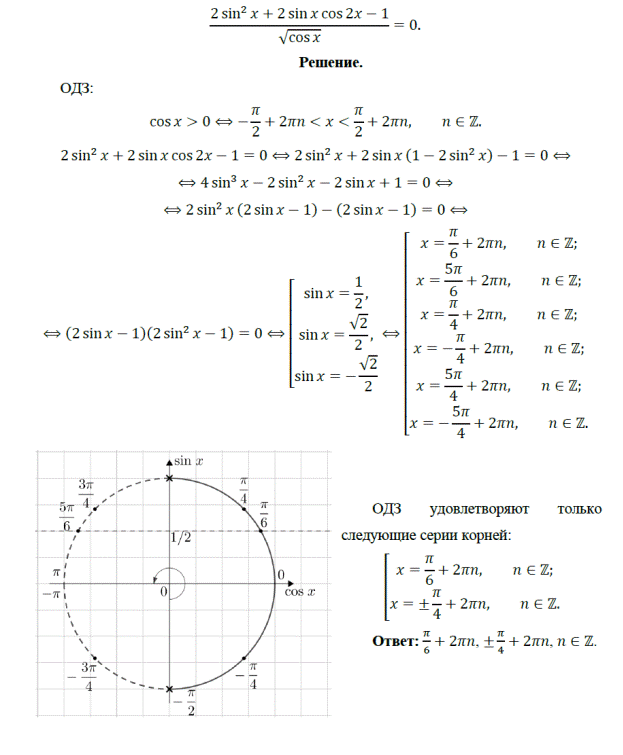
15. (Репетиционный ЕГЭ, 2011) Решите уравнение:

16. ( ЕГЭ, 2011) Решите уравнение:

17. ( ЕГЭ, 2011) Решите уравнение:

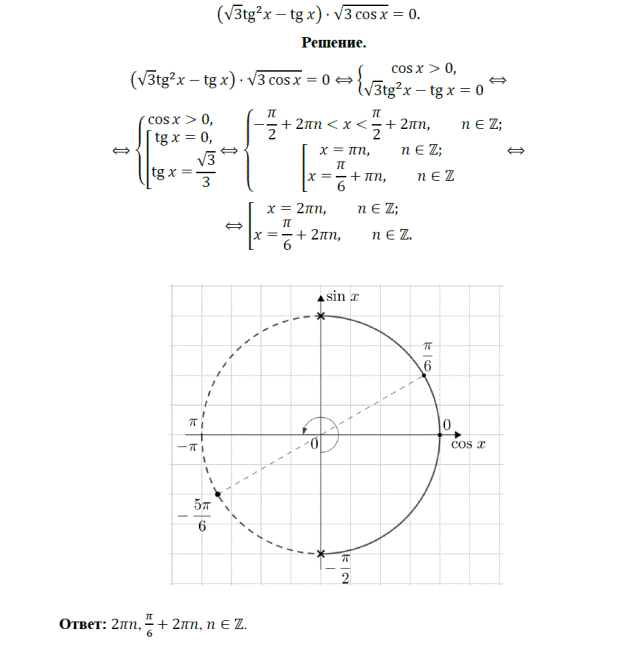
18. ( Пробный экзамен, 2012) Решите уравнение:

19. ( Пробный экзамен, 2012) Решите уравнение:

20. ( Пробный экзамен, 2013) Решите уравнение:

21. ( ЕГЭ, 2013) Решите уравнение:

22. ( ЕГЭ, 2013) Решите уравнение:

23. ( МИОО, 2014) Решите уравнение:

24. ( МИОО, 2014) Решите уравнение:

25. ( ЕГЭ, 2014) Решите уравнение:

26. ( ЕГЭ, 2014) Решите уравнение:

27. ( МИОО, 2015) Решите уравнение:

28. (МИОО, 2015) Решите уравнение:

29. (ЕГЭ, 2015) Решите уравнение:

30. (ЕГЭ, 2015) Решите уравнение:

31. (ЕГЭ, 2015) Решите уравнение:

32. (ЕГЭ, 2016) Решите уравнение:

33. (ЕГЭ, 2016) Решите уравнение:

34. (ЕГЭ, 2016) Решите уравнение:

35. (ЕГЭ, 2016) Решите уравнение:

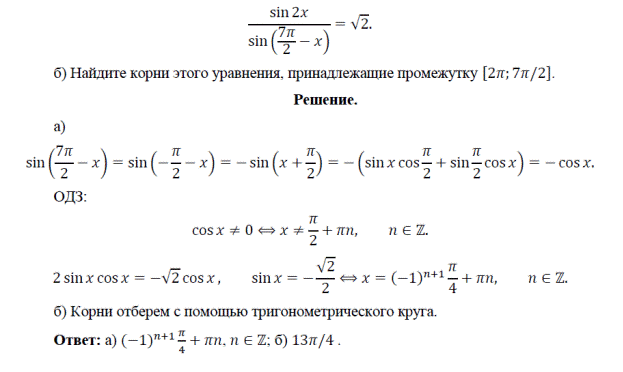
36. (ЕГЭ, 2017) Решите уравнение:

37. (ЕГЭ, 2017) Решите уравнение:

38. (ЕГЭ, 2017) Решите уравнение:

1129283568

Скачано с www.znanio.ru

Оглавление 1. Критерии оценивания выполнения задания №13 3 2

Критерии оценивания выполнения задания №13

Суммы суммы и разности тригонометрических уравнений 6)

Определение. Уравнения, в которых переменная стоит под знаком тригонометрической функции, называются тригонометрическими

Решение тригонометрических уравнений возведением обеих частей уравнения в квадрат

Восемь способов решения одного уравнения 1

Ответ: , ; , . 3.Приведение к однородному квадратному уравнению: ; ; ; ; (верно при любых ) ; ; или ; ; ,

; ; ; , ; , ; если , то , ; , ; если , то , ; , ; , . 5. разделим…

Если k – чётное, , то , следовательно , 1=1 верно если n – чётное, ,то , следовательно , 1=1 верно

Ответ: , ; , . Решим уравнение возведением в квадрат:

Ответ: , ; , . Проблемы, возникающие при решении тригонометрических уравнений 1

Решение тригонометрических уравнений из материалов

Репетиционный ЕГЭ, 2011) Решите уравнение:

Репетиционный ЕГЭ, 2011) Решите уравнение: 16

Пробный экзамен, 2012) Решите уравнение: 19

Пробный экзамен, 2013) Решите уравнение: 21

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

Посмотрите также