Сборник задач по физике на экстремум функции одной переменной

 

Задачи на экстремум функции одной переменной

с физическим содержанием.

 

Сборник задач.

 

 

Учебно-практическое пособие для учеников старших классов

с реализуемым физико-математическим профилем

 

 

Составитель:  Е.С. Воробейчикова, учитель математики МБОУ гимназия №9 г. Мурманска

 

 

 

ВВЕДЕНИЕ

 

В настоящем пособии содержатся задачи на экстремум функции одной переменной с физическим содержанием.

Наглядно демонстрирует применение производной в физических процессах. Все задачи содержат краткую теоретическую справку, решение, так же сопровождаются чертежами.

Учебное пособие расширяет опыт применения производной в практических задачах. Может использоваться в учебном процессе для аудиторных занятий, для самостоятельной работы.

 

Содержание.

 

Задача 1.   О максимальной мощности на участке цепи.

Задача 2.  О наименьшем расстоянии между частицами при их движении.

Задача 3.  О величине сопротивления прибора, влекущем максимальную мощность.

Задача 4.  О максимальном значении силы притяжения.

Задача 5.   О кинетической энергии дождевой капли.

Задача 6.   О наиболее вероятной скорости.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Задача 1.  Электрическая цепь состоит из источника тока с Э.Д.С., равной ε и внутренним сопротивлением равным r. Сопротивление внешнего участка R. При каком соотношении сопротивлений внутреннего и внешнего участков цепи мощность, выделяющаяся на внешнем участке цепи, будет максимальной?

Решение.

                                             Мощность P, выделяющаяся при

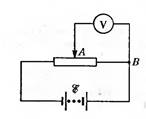
                                             прохождении  электрического тока в цепи, равна:

                                             Где    I – сила тока в цепи.

                                             По закону Ома для замкнутой цепи:

                        ,   Следовательно:  .

Будем рассматривать функцию P=P(R), где   I, ε и r  являются константами,

R – переменной.

Найдем производную данной функции 

 

Найдем значение переменной, при которой  производная равна 0.

 при R = r.

 

Ответ: при R = r мощность, выделяющаяся на внешнем участке цепи, будет максимальной.

 

Задача 2.  Две частицы движутся с постоянными скоростями v₁  и  v₂ по двум взаимно перпендикулярным прямым к точке их пересечения О. В момент времени t=0 частицы находятся на расстоянии и  от точки О.  Через какое время после этого расстояние между частицами станет наименьшим?   Чему оно равно?

Пусть расстояние между частицами равно S. Тогда его можно выразить по формуле:     (1).  Уравнения движения частиц   x=x(t)  и  y=y(t). , ,  .   Подставим в формулу (1): (2)

Решение:

 

 

 

                   

  

 

 

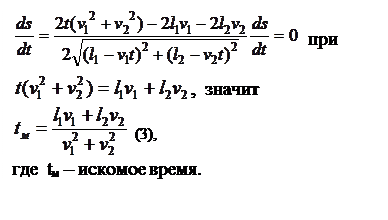
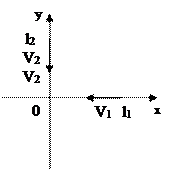
Если подставить (3) в (2), то получим: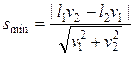

Ответ:    ;    .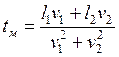

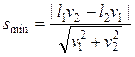Задача 3.  Электронагревательный прибор потребляет мощность от источника тока, ЭДС которого равна 3В, а внутреннее сопротивление равно 2Ом. Какое сопротивление должен иметь прибор, чтобы в нем выделялась максимальная мощность?

Решение:

Мощность, потребляемая электронагревательным прибором, сопротивление которого равно R, находится по формуле

.

Обозначим сопротивление прибора R = х. С учетом данных задачи составим функцию

.

Область определения этой функции - промежуток (0; + ).

Исследуем полученную функцию на экстремум.

Критические точки найдутся из уравнения

.

Критическими точками являются: х₁ = – 2 (точка не входит в область определения функции) и х₂ = 2.

Найдем знак производной на каждом промежутке: на промежутке (0; 2)         > 0; на промежутке  (2; +) < 0.  Так как при переходе через точку х = 2 производная меняет знак с плюса на минус, то в этой точке функция имеет максимум. Значит, мощность, потребляемая прибором, будет наибольшей, если сопротивление его равно 2 Ом.

Ответ: 2 Ом.

Задача 4.  Потенциальная энергия U поля частицы, в котором находится другая, точно такая же частица имеет вид: , где a и b — положительные постоянные, r — расстояние между частицами. Найти максимальное значение силы притяжения. 

 Решение:

Используем связь между потенциальной энергией поля U и F, получим

 Для определения F_max притяжения исследуем на экстремумы функцию:

   при r = r₁ = 3a/b;

Подставляя, получим

Ответ:  F(r)_max  при r = r₁ = 3a/b;

 

 

 

Задача 5.  Дождевая капля, начальная масса которой , падает под действием силы тяжести, равномерно испаряясь так, что убыль массы пропорциональна времени (коэффициент пропорциональности равен к). Через какое время после начала падения кинетическая энергия капли будет наибольшей. Каково ее значение?  Сопротивлением воздуха можно пренебречь.

Решение.

Кинетическая энергия тела вычисляется по формуле:

,   (1)

где m – масса капли в момент времени t,  v – ее скорость.

При свободном падении (2), где g – ускорение свободного падения, . - изменение массы капли со временем. Масса капли со временем изменится по закону (3). Соотношения (2) и (3) подставляем в (1).  Получим:

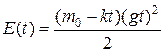
, при  ,   то есть при . Подставим это выражение для t в формулу (1) и получим
Ответ: ,

 

 

 

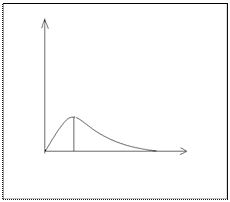
Задача 6.   Зная закон распределения молекул газа по скоростям, определить наиболее вероятную скорость.

Решение. Максвеловское распределение молекул идеального газа по скоростям имеет вид:  

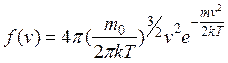   (1).

Здесь m₀ – масса одной молекулы, T – абсолютная температура, Т=const,

 v – скорость молекулы,  к=1,38·10^-23 Дж/к – постоянная Больцмана,

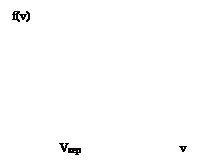
   ,  N – число молекул газа.

Скорость, при которой функция (1) имеет максимум, называется наиболее вероятной скоростью.

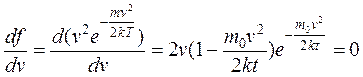
Тогда  V_вер=.

Ответ: V_вер=.

Литература

Берман Н. Г. Сборник  задач по курсу математического анализа. Решение типичных и трудных задач: Учебное пособие. 3-е изд., стер. – СПб.: Издательство «Лань», 2007. – 608 с.: (№ 1223. Стр. 103).

Смирнов В. И. Курс высшей математики. Т. 1. 23-е изд. Стер. – М. «Наука», 1974. – 480 с.

(3. Стр. 145.),

(75. Стр. 179 - 180).

Натансон И. П. Краткий курс высшей математики – Серия «Учебники для вузов. Специальная литература». –СПб.: Издательство «Лань», 1999. – 736 с.

(Задача 4. Стр. 210 - 212).

(Задача 6. Стр. 213).

Липман Б. Математический анализ Т. 1. Перевод с англ. Л. И. Головиной. Под ред И. М. Яглома. Учеб пособие для втузов, М., «Высш. школа», 1975.

(47. Стр. 211).

Пискунов Н.С. Дифференциальное и интегральное исчисление: Учеб. Для втузов. В 2-х т. Т. 1: − М.: Интеграл-Пресс, 2004. – 416 с.

(§ 7. Стр. 150 - 151).

Мышкис А. Д. Лекции по высшей математике. Изд. 4-е. Стер. . – М. «Наука», 1973. – 640 с.

(Пример3, Стр. 147).

Бермант А. Ф., Араманович И. Г. Краткий курс математического анализа. Учебник для вузов. 11-е изд., стер. – СПб.: Издательство «Лань», 2005. – 736 с.: ил. – (Учебники для вузов. Специальная литература).

( 2). Стр. 194 - 195).

Волькенштейн В. С., Сборник задач по общему курсу физики. Изд 3-е, испр. и доп. – СПб.: Книжный мир, 2005. – 328 с.

(№№ 2.89;  ).

Чертов А.Г., Воробьёв А.А. Задачник по физике: Учеб. Пособие для втузов. – 7-е изд., перераб. И доп. – М.: Издательство Физико-математической литературы, 2001. – 640 с.

Натансон И. П. Простейшие задачи на максимум и минимум. Государственное издательство технико ‑ теоретической литературы. М ‑ Л.: ‑ 1950 ‑32 с.

(§ 9. Задача 5. Стр. 14 ‑ 15),

(§ 16. Задача 11. Стр. 21 ‑ 22),

(§ 22. Стр. 27 – 28).