Добавить материал

и получить 10 документов
и свидетельство автора

Савватеев Андрей Сергеевич

Сборник задач по гидравлике

pdf
24.09.2023

Публикация педагогических разработок

Бесплатное участие. Свидетельство автора сразу.
Мгновенные 10 документов в портфолио.

Добавить материал

Сборник задач ПСКГУ.pdf

Федеральное агентство по образованию псковский государственный

политехнический институт

О. В. Ворожцов

Гидравлика с примерами решения задач

Учебно–методическое пособие

для студентов специальности 653300 –

Эксплуатация наземного транспорта и транспортного оборудования

Псков

2008

Введение

Гидравлика – это наука, изучающая законы равновесия и движения жидкостей, а также законы взаимодействия жидкостей с окружающими их граничными поверхностями и с твердыми или упругими телами, погруженными (частично или полностью) в жидкость.

Название "гидравлика" произошло от греческих слов "хюдор" - вода и "аулос" - труба, желоб. В настоящее время почти во всех областях техники применяют различные гидравлические устройства, основанные на использовании гидравлических законов. Главнейшие области применения гидравлики – гидротехника, мелиорация и водное хозяйство, гидроэнергетика, водоснабжение и канализация, водный транспорт, машиностроение, авиация и т. д.

При исследовании гидравлических явлений в гидравлике применяют теоретический и экспериментальный методы.

В теоретическом методе используют уравнения механики для математического описания практически всех процессов, происходящих в движущейся жидкости. Ввиду сложности строения жидкостей теоретические исследования проводят для модельных жидкостей, что облегчает применение уравнений механики. Например, применяют модель невязкой жидкости, которая в отличие от существующих в природе реальных жидкостей лишена свойства вязкости. Этот метод привел к созданию теоретической гидромеханики, имеющий строго математический характер. Однако использование этих математических моделей не всегда позволяет решать практические задачи. Это связано, с одной стороны, со сложностью используемых математических зависимостей, а с другой стороны – с необходимостью учета влияния большого числа конструктивных факторов.

Экспериментальные исследования в гидравлике имеют важное значение. Леонардо да Винчи (1452 – 1519 г.г.), написавшему работу "О движении и измерении воды", которая была опубликована спустя более чем 400 лет после его смерти, принадлежат слова: "Всякий раз, когда имеешь дело с водой, прежде всего обратись к опыту, а потом уже рассуждай". Изучение гидравлических явлений на моделях, созданных на основе теории подобия с применением определенных методик моделирования, позволяет получить данные о параметрах, которыми будет характеризоваться явление в реальных условиях.

Оптимальное сочетание теоретических и экспериментальных исследований позволяет получить результат, достаточно точно описывающий исследуемое явление.

Раздел 1 Жидкости и их физические свойства

1.1. Жидкости. Гипотеза сплошности. Силы, действующие в жидкости.

Жидкости. Все вещества в природе имеют молекулярное строение. По характеру молекулярных движений, а также по числовым значениям межмолекулярных сил жидкости занимают промежуточное положение между газами и твердыми телами.

Молекулы жидкости находятся в непрерывном хаотичном тепловом движении, осуществляющемся в виде колебаний (10¹³ колебаний в секунду) относительно мгновенных центров и скачкообразных переходов от одного центра к другому. Тепловое движение молекул твердых тел – колебания относительно стабильных центров, тепловое движение молекул газа – непрерывные скачкообразные перемены мест.

Жидкими телами или жидкостями называют физические тела, легко изменяющие свою форму под действием самой незначительной по величине силы. Можно сказать, что жидкость – это физическое тело, обладающее текучестью, имеющее определенный объем и заполняющая часть пространства (сосуда), равного ее объему.

Различают два вида жидкостей: -жидкости капельные (малосжимаемые); -жидкости газообразные (сжимаемые).

Газообразные жидкости (газы) в отличие от жидкостей капельных заполняют все предоставленное им пространство и изменяют свой объем в зависимости от изменения температуры и давления. Газообразные жидкости, их свойства и применение рассматриваются в специальных дисциплинах – термодинамике и аэромеханике.

В гидравлике рассматривается равновесие и движение капельной жидкости, в дальнейшем называемое просто жидкостью. Капельные жидкости представляют собой жидкости в обычном, общепринятом понимании этого слова (вода, нефть, керосин и т. д.)

Гипотеза сплошности. В гидравлике жидкость рассматривают как деформируемую систему материальных точек (частиц), непрерывно заполняющих пространство, в котором она движется.

Предполагают, что частица жидкости представляет собой бесконечно малый объем, в котором находится достаточно много молекул жидкости. Например, в кубике воды со сторонами размером 0,01 мм будет находиться 3,3×10¹³ молекул.

При таком предположении жидкость в целом рассматривают как сплошную среду (континуум), непрерывно заполняющую пространство, т. е. принимают, что в жидкости нет пустот или разрывов. Ввиду большого количества молекул, составляющих частицу жидкости, влияние отдельных молекул не учитывается.

Сплошная среда представляет собой модель, которую успешно используют при исследовании закономерностей покоя и движения жидкости.

Силы, действующие в жидкости. Вследствие текучести жидкости она не воспринимает сосредоточенные силы, поэтому в жидкости действуют только распределенные по объему или по поверхности силы. Поэтому силы, действующие на жидкость, принято делить на массовые (объемные) и поверхностные.

Массовые (объемные) силы – это силы, действующие на каждую частицу жидкости с массой ∆m, то есть это силы, распределенные по массе. К ним относятся: сила тяжести, сила инерции (кариолисова сила инерции, переносная сила инерции), гравитационные силы.

Поверхностные силы – это силы, действующие на каждый элемент поверхностей ∆S, ограничивающих жидкость, и на каждый элемент поверхностей, проведенных произвольно внутри жидкости.

Пусть на плоскую поверхность площадью ∆S действует сила ∆R (рис. 1.1). Силу ∆R можно разложить на нормальную ∆р и тангенциальную ∆Т составляющие.

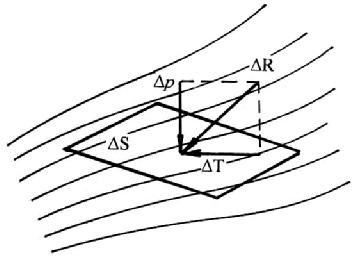
Рис. 1.1. Схема действия поверхностных сил

Тангенциальная составляющая ∆Т называется силой трения и вызывает в жидкости касательные напряжения. Среднее напряжение трения τ, действующее касательно к площади ∆S, будет равно:

τ _ср= ^∆Т ∆S .

Среднее касательное напряжение не дает точного значения касательного напряжения в любой точке площади ∆S. Поэтому касательное напряжение в данной точке равно пределу, к которому стремится отношение силы трения ∆Т к площади ∆S, касательно к которой она действует, при уменьшении ∆S до нуля, т. е. при стягивании ее к размерам точки:

τ = lim_{∆ →}^∆ ∆S . (1.1)

Выражение (1.1) можно назвать плотностью распределения касательных сил (сил трения) по площади ∆S.

Единицей измерения касательных напряжений в системе СИ является паскаль (Па) – ньютон, отнесенный к квадратному метру (1 Па = 1 Н/м²).

Нормальная сила ∆р называется силой давления и вызывает в жидкости нормальные напряжения сжатия. Если сила давления ∆р равномерно распределена по площадке ∆S, то среднее (единичное) давление будет равно:

р_ср=∆ ∆S .

Плотность распределения нормальных сил:

р = lim_{∆ →}^∆ ∆S . (1.2)

За единицу давления в системе СИ принят паскаль

(1 Па = 1 Н/м²). Раньше давление измерялось в кгс/см²(1 кгс/см² = 1 атмосфера).

Поскольку при применении единицы "паскаль" получаются большие цифровые значения, ее заменяют на бары: 1 бар = 100 000 Па. Итак, соотношения между различными единицами измерения давления следующие:

1 кгс/см² = 1 ат = 1 бар = 0.1 МПа.

1.2. Плотность жидкости.

Важнейшими характеристиками механических свойств жидкости являются ее плотность и удельный вес. Они определяют "весомость" жидкости.

Плотность ρ характеризует распределение массы ∆m жидкости по объему ∆W. В произвольной т.а жидкости плотность распределения массы равна: ра = lim∆ → ∆m ∆W ,

где ∆m –масса, заключенная в объеме ∆W, стягиваемом в точку а.

Плотность однородной жидкости равна отношению массы m жидкости к ее объему:

ρ =^m W . (1.3)

Плотность ρ во всех точках однородной жидкости одинакова. В общем случае плотность может изменяться в объеме жидкости от точки к точке и в каждой точке объема с течением времени. За единицу плотности в системе СИ принят 1 кг/м³.

Вместо плотности в формулах может быть использован также удельный вес γ (Н/м³), то есть вес жидкости G, приходящийся на единицу объема W:

γ = ^G W = ^mg W = ρg. (1.4)

Плотность жидкостей и газов зависит от температуры и давления. Все жидкости, кроме воды, характеризуются уменьшением плотности с увеличением температуры. Плотность воды максимальна при t =4 ºС и уменьшается как с уменьшением, так и с увеличением температуры от этого значения. В этом проявляется одно из аномальных свойств воды.

Плотность воды при t =4º С составляет 1000 кг/м³; морской воды - 1020 … 1030 кг/м³; нефти и нефтепродуктов – 650 … 900 кг/м³; чистой ртути - 13600 кг/м³; воздуха при t =0º С и атмосферном давлении – 1,29 кг/м³.

При изменении давления плотность жидкости изменяется незначительно.

1.2. Физические свойства жидкостей.

Сжимаемость. Это свойство жидкостей изменять объем при изменении давления; характеризуется коэффициентом объемного

сжатия (коэффициентом сжимаемости) β_р(Па^-1); представляющим

собой относительное изменение объема жидкости W при изменении давления на единицу:

β_р= – , (1.5)

где W – первоначальный объем жидкости; dW – относительное изменение объема жидкости при изменении давления на величину dр. Знак "—" в формуле (1.5) указывает на то, что при увеличении давления объем жидкости уменьшается. На рис. (1.2) можно видеть зависимость сжимаемости жидкости от ее химической природы.

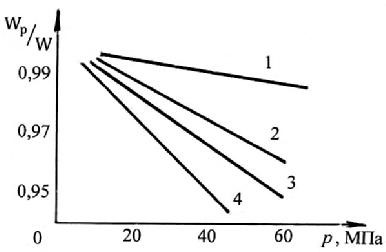
Рис.1.2. Зависимость сжимаемости различных жидкостей от давления:

1 – глицерин; 2 – вода; 3 – масло; 4 – силиконовая рабочая жидкость

Изменение плотности при изменении давления учитывается формулой (1.6):

ρ ≈ 1 – β_рd , (1.6)

где ρ и ρ₁ –плотность жидкости при давлении р и р₁ соответственно; dр –перепад давлений (dр = р – р₁).

Величина, обратная коэффициенту объемного сжатия – модуль объемной упругости жидкости Е_о, (Па):

Е_о = ¹ _β_р . (1.7)

Физический смысл объемного модуля упругости можно представить, если считать, что W = 1 м³, а dр = 1 Па. Тогда Е_о = ¹ dW , то

есть модуль упругости можно представить как величину, обратную изменению объема одного кубического метра жидкости при изменении давления на одну единицу.

Объемный модуль упругости жидкости зависит от типа жидкости, давления и температуры. Однако в большинстве случаев Е_осчитают постоянной величиной, принимая за нее среднее значение в данном диапазоне температур и давлений.

Различают изотермический и адиабатический модуль упругости. Причем для расчетов обычно используют изотермический модуль упругости Е_то, применяемый для анализа медленных процессов, при которых успевает завершиться теплообмен с окружающей средой. Для быстротечных процессов, при которых теплообмен не успевает завершиться, используют адиабатический модуль упругости Е_ао.

Сжимаемость жидкостей очень незначительна, и в большинстве случаев ее можно считать несжимаемой. Однако, если бы вода в Мировом океане (средняя глубина 3704 м) была несжимаемой, ее уровень повысился бы на 27 м. Объем легкого минерального масла, применяемого в жидкостных амортизаторах шасси самолетов при нормальной температуре, уменьшается при повышении давления от 0 до 35 МПа на 1,7 %, а керосина – на 0,8 %.

Сжимаемость рабочих жидкостей приводит к понижению жесткости гидравлической системы, а следовательно, к потере передаваемой мощности.

Температурное расширение. Это свойство жидкостей изменять объем при изменении температуры; характеризуется температурным коэффициентом объемного расширения β_t(1/°С), представляющим собой относительное изменение объема жидкости при изменении температуры на единицу (1 ºС) и при постоянном давлении:

β_t= , (1.8)

где W – первоначальный объем жидкости; dW – относительное изменение объема жидкости при повышении температуры на dt.

Для большинства жидкостей коэффициент β_tс увеличением давления уменьшается (рис. 1.3).

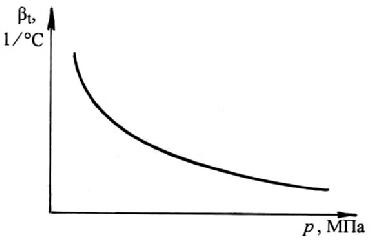
Рис. 1.3. Зависимость коэффициента объемного расширения β_tот давления р

Для воды с увеличением давления при температуре до 50 ºС коэффициент β_tрастет, а при температуре выше 50 ºС уменьшается.

В общем случае для капельных жидкостей значение β_tневелико, и обычно при расчетах не учитывается. Однако в ряде случаев при больших перепадах температуры изменение плотности жидкости приходиться учитывать:

ρ ≈ 1 + β∆t , (1.9)

где ρ и ρ₁– плотности при температурах t и t₁ (∆t = t – t₁).

Вязкость. Это свойство жидкости оказывать сопротивление относительному сдвигу ее слоев.

Вязкость проявляется в том, что при относительном перемещении слоев жидкости на поверхностях их соприкосновения возникают силы сопротивления сдвигу, называемые силами внутреннего трения или силами вязкости. Благодаря этим силам слой жидкости, движущийся медленнее, "тормозит" соседний слой, движущийся быстрее. Силы внутреннего трения проявляются вследствие наличия межмолекулярных связей между движущимися слоями.

Силы внутреннего трения в жидкости впервые были обнаружены Ньютоном в 1686 г., а затем экспериментально обоснованы проф. Н. П. Петровым в 1883 г.

Для выяснения физической сущности понятия вязкости рассмотрим следующую схему (рис. 1.4).

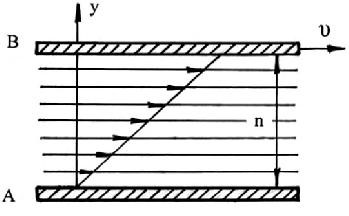
Рис. 1.4. Схема течения жидкости между двумя пластинами

Пусть имеются две параллельные пластины А и В, в пространстве между которыми заключена жидкость; нижняя пластина А неподвижна, верхняя пластина В движется поступательно с некоторой постоянной скоростью υ. Слои жидкости, непосредственно прилегающие к пластинам ("прилипшие" слои), будут иметь одинаковые с ними скорости, т. е. слой, прилегающий к верхней пластине В, будет двигаться со скоростью υ , а слой, прилегающий к нижней пластине А, будет находиться в покое.

Промежуточные слои жидкости будут скользить друг по другу, причем их скорости будут пропорциональны расстояниям от нижней пластины.

Если расстояние между пластинами обозначить через n, то скорость υ_yслоя жидкости, находящегося на расстоянии y от этой пластины, будет равна:

υ_y = υ .

Ньютоном было высказано предположение, впоследствии подтвержденное опытом, что силы сопротивления, возникающие при таком скольжении, пропорциональны площади соприкосновения слоев и скорости скольжения. Принимая площадь соприкосновения равной единице, получим:

τ = μ , (1.10)

где τ – сила сопротивления, отнесенная к единице площади (касательное напряжение), μ – коэффициент пропорциональности, учитывающий особенности конкретных жидкостей и называемый коэффициентом динамической вязкости жидкости, dυ/dy – градиент скорости (скорость деформации сдвига), то есть величина изменения скорости в направлении, нормальном к направлению вектора самой скорости. В данном случае dυ/dy = υ/n.

При слоистом прямолинейном течении жидкости в цилиндрической трубе круглого поперечного сечения жидкость движется кольцевыми цилиндрическими слоями толщиной dy , скорость слоев уменьшается от оси к стенкам трубы и максимальна в центре по оси трубы (рис. 1.5.).

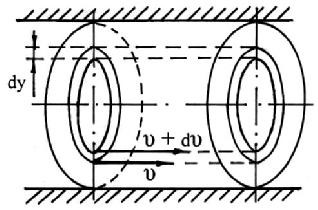
Рис. 1.5 Схема движения жидкости в цилиндрической трубе

Разность скоростей в соседних слоях равна dυ (рис. 1.6). Касательное напряжение в данном случае согласно формуле (1.10) равно:

τ = ±μ . (1.11)

Знак "+" или "-" указывает направление отсчета расстояний (от стенки рассматриваемой трубы или от ее оси). Градиент скорости может быть положительным, если расстояние отсчитывается от стенки трубы, или отрицательным (от ее оси).

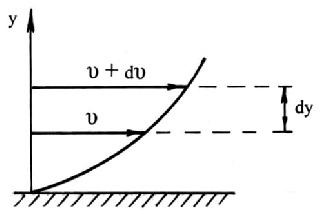
Рис. 1.6. Профиль скоростей при течении вязкой жидкости вдоль стенки

Напряжения трения возможны лишь в движущейся жидкости, т.е. вязкость жидкости проявляется лишь при ее течении. Жидкости, для которых справедлив закон внутреннего трения Ньютона, называются ньютоновскими.

Существуют жидкости (коллоидные суспензии, растворы полимеров, гидросмеси из глины, цемента, строительные растворы и т.п.), для которых связь между касательным напряжением τ и скоростью сдвиговой деформации dυ/dy будет выражаться соотношением:

τ = τ_о + μ . (1.12)

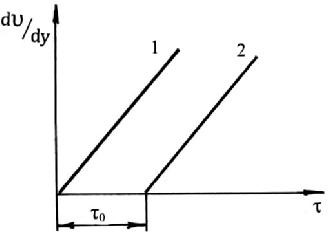
Рис. 1.7. Зависимость между касательным напряжением для обычных (1) жидкостей и вязкопластичных (2)

Такие жидкости относятся к неньютоновским и называются вязкопластичными или аномальными. Опытами установлено, что в подобных жидкостях движение наступает только после того, как касательные напряжения достигнут некоторого предельного минимального значения, обычно называемого начальным напряжением сдвига.

Таким образом, вязкопластичные жидкости отличаются от ньютоновских наличием касательного напряжения в состоянии покоя τ_о.

В память французского ученого Пуазейля единица вязкости была названа "пуаз" с). В системе СИ единицей динамической вязкости является Па·с = с = 10 П.

В гидравлических расчетах кроме динамической вязкости используют понятие кинематической вязкости, равное отношению динамической вязкости μ к плотности жидкости ρ:

ν = . (1.13)

Единицей кинематической вязкости в системе СИ принята единица см²/с, названная в честь английского ученого Стокса "стокс"; 1 м²/с = 10⁴ Ст. Сотая доля стокса называется сантистоксом (сСт).

Вязкость капельных жидкостей зависит от температуры и уменьшается с увеличением последней (рис. 1.8).

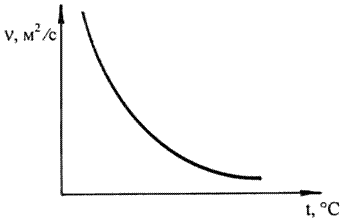
Рис. 1.8. Зависимость кинематической вязкости от температуры

Вязкость жидкостей зависит также от давления, однако эта зависимость существенно проявляется лишь при относительно больших изменениях давления (в несколько десятков МПа). С увеличением давления вязкость большинства жидкостей возрастает. Исключением является вода, для которой при температуре до 32 ºС с увеличением давления вязкость уменьшается.

С целью облегчить и упростить ряд теоретических выводов и исследований в гидравлике существует понятие "идеальная" жидкость. Ее считают абсолютно несжимаемой, она обладает полным отсутствием температурного расширения и не оказывает сопротивления сдвигающим и растягивающим усилиям. Идеальная жидкость – жидкость фиктивная. Но сжимаемость, температурное расширение и сопротивление растяжению для реальных жидкостей ничтожно малы и обычно не учитываются. Таким образом, основной и единственной особенностью, отличающую реальную жидкость от идеальной, является наличие у реальной жидкости сил сопротивления сдвигу, определяемых особым свойством жидкости – вязкостью. Поэтому идеальную жидкость иногда называют невязкой, а реальную - вязкой жидкостью.

Вязкость жидкостей измеряют при помощи вискозиметров. В различных странах для определения вязкости используют вискозиметры Энглера (в Европе), Сейболта (в США), Редвуда (в Великобритании). Существуют автоматические системы измерения кинематической и динамической вязкости.

Растворение газов. Все жидкости в той или иной мере поглощают и растворяют газы. Относительное количество газа, которое может раствориться в жидкости до ее насыщения, прямо пропорционально давлению на поверхности раздела.

Объем растворенного газа вычисляется по формуле:

W_г = k_гW_ж , (1.14)

где W_г – объем растворенного газа, отнесенный к нормальным условиям (p_o, t_o); W_ж - объем жидкости; p - давление жидкости; p_o - эталонное давление (например, атмосферное); k_г - коэффициент растворимости газа в жидкости (объем газа, растворяющегося при атмосферном давлении в единице объема жидкости).

Растворимость воздуха в реальной жидкости до ее насыщения зависит от ее вида и плотности. Предельное значение коэффициента растворимости k_г могут достигать 0,12-0,2.При температуре 20 ºС и атмосферном давлении в воде содержится 1,6% растворенного воздуха по объему. При повышении температуры коэффициент растворимости уменьшается.

При понижении давления растворенный газ выделяется, ухудшая характеристики работы гидравлических систем. Это может произойти, например, в результате внезапного расширения потока жидкости или вследствие больших местных скоростей.

Нарушение сплошности движущейся жидкости вследствие местного понижения давления ниже критического называется кавитацией (от латинского "кавитас" - полость).

В гидроприводе пузырьки, перемещаясь с потоком жидкости, попадают в область с высоким давлением или низкой температурой и мгновенно смыкаются. В этот момент пар конденсируется и газы снова растворяются в жидкости. В образовавшиеся пустоты с большими скоростями устремляются частицы жидкости, что приводит к местным гидравлическим ударам (резкому и значительному повышению давления в этих местах) и звуковым импульсам.

Кавитация в обычных случаях является нежелательным явлением и приводит к:

- уменьшению КПД гидромашины;

- кавитационной коррозии металла;

- уменьшению пропускной способности трубопровода;

- повышению температуры жидкости;

- термоокислению жидкости (воспламенение паров и сгорание частиц жидкости в среде воздушного пузырька – эффект Дизеля, что приводит к образованию в жидкости нерастворимых коксообразующих продуктов).

Испарение. Это свойство капельной жидкости изменять свое агрегатное состояние, в частности превращаться в пар.

Интенсивность испарения (парообразования), происходящего на свободной поверхности жидкости, зависит от рода самой жидкости и условий, в которых она находится. Одним из показателей, характеризующих испаряемость жидкости, является температура ее кипения при нормальном атмосферном давлении – чем выше температура кипения, тем меньше испаряемость. Кипение – это процесс перехода жидкости в газообразное состояние, происходящий внутри жидкости. Температура кипения с повышением давления на ее поверхности увеличивается.

Если испарение происходит в свободном пространстве, то почти все молекулы, перешедшие при испарении в паровую фазу, удаляются с поверхности жидкости и обратно не возвращаются.

Если жидкость находится в замкнутом пространстве, то после достижения в нем определенной концентрации паров устанавливается равновесие между процессами испарения и конденсации, и давление пара становится постоянным. Такой пар, находящийся в замкнутом пространстве в термодинамическом равновесии с жидкостью (число молекул, вырывающихся в единицу времени из жидкости и переходящих в паровую фазу, равно числу молекул, возвращающихся в жидкость за то же время), называют насыщенным. А его давление – давлением насыщенного пара при данной температуре.

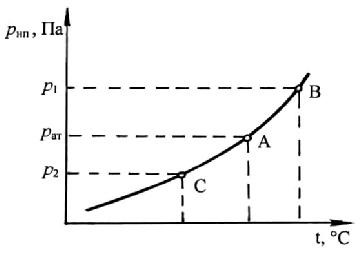
Рис. 1.9. Зависимость давления насыщенных паров от температуры

На рис. 1.9. приведена зависимость давления насыщенных паров р_н.п. воды от температуры. Точка А соответствует температуре 100 ºС и нормальному атмосферному давлению. При повышении давления на свободной поверхности жидкости до значения р₁ температура кипения воды повысится до некоторого значения t. При понижении давления температура кипения понизится.

Обычно при понижении давления до давления насыщенных паров жидкости (при данной температуре) в жидкости образуются пузырьки газа, выделившегося из жидкости, т.е. происходит так называемое "холодное кипение".

Если парообразование происходит в закрытом сосуде, то оно сопровождается повышением давления. Процесс идет по линии от точки С к точке А, затем В и далее (рис.1.9.), что может привести к разрушению сосуда.

Поверхностное натяжение. Является специфическим свойством жидкостей и связано с ее молекулярной структурой. В результате притяжения между молекулами жидкости возникают силы сцепления. Внутри жидкости эти силы уравновешиваются, однако находящиеся на границе раздела поверхности жидкости с газом, твердым телом или двумя несмешиваемыми жидкостями молекулы жидкости испытывают неуравновешенное извне воздействие (отсутствие притяжения со стороны молекул газа). Поэтому появляется сила, направленная внутрь объема жидкости, называемая силой молекулярного давления. Эта сила стремится придать объему жидкости форму с наименьшей поверхностью.

Чтобы увеличить поверхность жидкости, необходимо часть внутренних молекул вывести на поверхность, для чего придется совершить работу. Это можно представить как наличие сопротивления граничной поверхности жидкости растяжению и считать, что по поверхности распределены силы, препятствующие растяжению. Эти силы действуют по касательным к поверхности жидкости направлениям и называются силами поверхностного натяжения.

Поверхностное натяжение σ (Н/м) представляет собой удельную, отнесенную к единице площади, свободную поверхностную энергию, которой обладают молекулы поверхностного слоя. У большинства жидкостей при 20 ºС σ = 0,01…0,1 Н/м.

В трубках малого диаметра (капиллярах) наблюдается искривление свободной поверхности жидкости, граничащей с газом. Если поверхность трубки смачивается, то свободная поверхность жидкости в трубке вогнутая. Если нет смачивания, то свободная поверхность выпуклая. В этих случаях силы поверхностного натяжения обуславливают дополнительное напряжение в жидкости.

Под действием этих напряжений в трубках малого диаметра происходит капиллярное поднятие (при смачивании) или опускание (если смачивания нет) жидкости на некоторую высоту. Чем меньше диаметр, тем выше или ниже уровень жидкости.

Силы поверхностного натяжения приходится учитывать при движении жидкости в трубках малого диаметра (капиллярных трубках) некоторых измерительных приборов. При обычных гидравлических расчетах влиянием этих сил ввиду их малости пренебрегают.

Поднятие воды в капиллярах почвы и грунта - важный фактор распространения воды. Высота капиллярного поднятия воды в грунтах изменяется от нуля почти до 5 м (в глинистых почвах).

1.2. Примеры решения задач.

1.2.1. Сосуд заполнен водой, занимающей объем W₁= 2 м³. На сколько уменьшится и чему будет равен этот объем при увеличении давления на величину на величину 200 бар при температуре 20 ºС ? Модуль объемной упругости для воды при данной температуре

Е_о= 2110 МПа.

Изменение объема жидкости определим из уравнения (1.5):

∆W = – β_p W ∆p.

Коэффициент объемного сжатия определим из уравнения (1.7):

βp = 1 Е = · = 4,74·10 1/Па.

Увеличение давления ∆р = 200 бар = 20·10 Па. Тогда:

∆W = 4,74·10·2·20·10 = 0,019 м³.

Искомый объем будет равен:

W₂ = W₁ – ∆W = 1,981 м³.

1.2.2. Канистра, заполненная бензином и не содержащая воздуха, нагрелась на солнце до температуры 50 ºС. На сколько повысилось бы давление бензина внутри канистры, если бы она была абсолютно жесткой? Начальная температура бензина 20 ºС. Модуль объемной упругости бензина принять равным Е_о =1300 МПа, коэффициент температурного расширения β_t = 8ּ10 1/град.

Из уравнения (1.8) находим относительное изменение объема бензина при увеличении температуры ∆t на 30 ºС (∆t = t₂ – t₁ = 30 ºС): ^∆W W = β_t ∆t = 8ּ10ּ30 = 0,024.

Из уравнения (1.5) находим изменение давления ∆р при увеличении температуры ∆t на 30 ºС:

∆ ∆ ⁶= 31,2 МПа.

∆р = = Е_о= 0,024 ּ 1300ּ10 р

1.2.3. Плотность масла АМГ-10 при температуре 20 ºС составляет 850 кг/м³. Определить плотность масла при повышении температуры до 60 ºС и увеличении давления с атмосферного (р₁=0,1 МПа) до р₂=8,7 МПа. Модуль объемной упругости масла Е_о =1305 МПа, температурный коэффициент β_t = 0,0008 1/град.

Плотность масла при повышении температуры до значения t₂= 60 ºС вычислим по формуле (1.9):

ρ_I = ρ 1 + β∆t = 850 1 + 0,0008 · (60 − 20) = 823,6 кг/м³.

Плотность масла при повышении давления до значения p₂= 8,7 МПа вычисляем по формулам (1.6) и (1.7):

ρII = ρ 1 – βрd = ( I ) Е = , · , · = 829 кг/м3.

1.2.4. Определить объемный модуль упругости жидкости, если под действием груза А массой 250 кг поршень прошел расстояние ∆h = 5 мм. Начальная высота положения поршня (без груза) H = 1,5 м; диаметр поршня d = 80 мм и резервуара D = 300 мм; высота резервуара h = 1,3 м. Весом поршня пренебречь. Резервуар считать абсолютно жестким. -

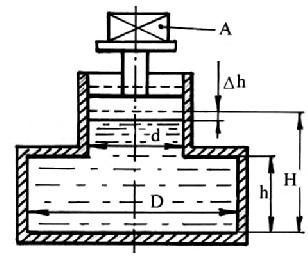
Сила тяжести, создаваема грузом А, будет равна:

F = mg = 2450 Н.

Давление, создаваемое этой силой (т.е. приращение давления dр), определим как:

dр = F S_п= 4F πd = 4 · 2450 3,14 · 0,08 = 490 кПа.

Первоначальный объем W жидкости равен:

W = S₁h + S₂(H – h) = h + (H – h) = 0,093 м .

Изменение объема равно:

dW = S2 ∆h = ∆h = 2,5 ּ10 м3.

Модуль объемной упругости определим по формулам (1.5) и

(1.7):

Е_о =W Па =1814 МПа.

= 0,1· = 0,1814

1.2.5. Контрольные вопросы.

1. В чем заключается гипотеза сплошности жидкости?

2. Что такое плотность жидкости, от чего она зависит?

3. Какие силы относятся к массовым и поверхностным? Какие виды напряжений действуют в жидкости?

4. В чем состоит физический смысл объемного модуля упругости?

5. Что такое вязкость жидкости?

6. Какова связь кинематической и динамической вязкости?

7. Поясните природу неньютоновских жидкостей.

8. Какие причины вызывают кавитацию?

9. Что такое "холодное" кипение?

10. Какова природа явления поверхностного натяжения?

Раздел 2 Гидростатика

2.1. Гидростатическое давление и его свойства.

Гидростатикой называется раздел гидравлики, в котором изучаются законы равновесия жидкостей и рассматриваются практические приложения этих законов.

Рассмотрим некоторый объем жидкости массой М, находящийся в состоянии относительного покоя (рис. 2.1).

Рассечем объем, занимаемый жидкостью, произвольной плоскостью АВ на две части, содержащие соответственно массы М₁ и М₂, и отбросим одну из них (например, правую). Чтобы сохранить равновесие оставшейся в левой части массы жидкости М₁, необходимо приложить силу, эквивалентную действию отброшенной массы М₂. Эта сила ∆р будет равномерно распределена по площади сечения ∆S. Тогда отношение

∆

р_ср= , (2.1)

∆

представляющее собой среднюю силу, действующую на единицу площади ∆S, будет называться средним гидростатическим давлением.

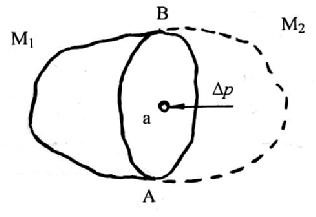
Рис.2.1. Схема для определения гидростатического давления

В общем случае величина среднего давления р_ср будет тем меньше отличаться от истинного значения давления, например в точке а, чем меньше будет площадь сечения ∆S, т.е. истинное гидростатическое давление равно:

р_а= → lim ^∆ ∆S . (2.2)

Сила, действующая на единицу площади ∆S при стремлении (стягивании) этой площади к размерам точки А, называется силой гидростатического давления.

Рассмотрим основные свойства гидростатического давления:

1.Сила гидростатического давления всегда направлена по нормали к площадке действия. Действительно, если бы сила ∆р (рис.2.1) была направлена не по нормали к площадке ∆S, то эту силу можно было бы разложить на составляющие: нормальную и касательную к площадке ∆S. Из-за текучести жидкости касательная составляющая привела бы жидкость в движение, то есть в этом случае равновесие жидкости было бы невозможно.

Поскольку жидкость не сопротивляется растягивающим усилиям (сопротивление растяжению может происходить только в дегазированных жидкостях), то сила ∆р может быть только сжимающей. Таким образом, по любой поверхности, проведенной внутри покоящейся жидкости, всегда действует только распределенная сжимающая сила.

2.В покоящейся жидкости величина давления не зависит от ориентации в пространстве площадки, на которую она действует.

Доказательство этого свойства сводится к определению равенства сил, действующих на боковые грани тетраэдра (рис.2.2), то есть: р_х = р_y= р_z= р_n.

Доказательство этого равенства можно найти в любой учебной литературе по гидравлике.

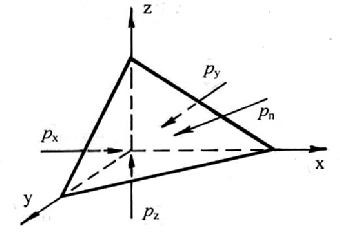
Рис.2.2 Схема для доказательства свойства гидростатического давления

3. Гидростатическое давление может быть неодинаковым в различных точках покоящейся жидкости, т.е. зависит от координаты точки в пространстве: р = f(x, y, z).

2.2. Основное уравнение гидростатики.

Рассмотрим случай равновесия жидкости, когда на нее действует лишь одна массовая сила – сила тяжести, и получим уравнение, позволяющее находить гидростатическое давление в любой точке рассматриваемого объема жидкости.

Пусть на свободную поверхность жидкости, находящуюся в сосуде, действует давление р_о(рис.2.3).

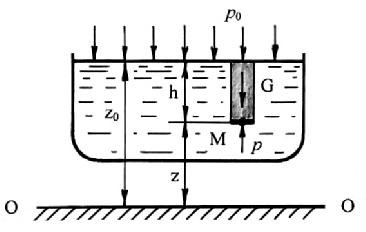
Рис 2.3 Схема для вывода основного уравнения гидростатики

Определим давление р в произвольно выбранной точке М, которая находится на глубине h. Выделим около точки М элементарную (бесконечно малую) площадку dS, и построим на ней до свободной поверхности вертикальный цилиндрический объем высотой h. Вес жидкости в указанном объеме равен:

G = Mg = ρ·g·h·dS. (2.3)

Давление жидкости р на нижнее основание цилиндра будет направлено по нормали вверх. Запишем сумму сил, действующих на выделенный объем в проекции на вертикальную ось: рdS - р_оdS – ρghdS = 0

После сокращения выражения на dS и перегруппировки членов получим:

р = р_о + ρgh = р_о + γh. (2.4)

Полученное уравнение называют основным уравнением гидростатики, оно позволяет подсчитать давление в любой точке внутри покоящейся жидкости.

Из уравнения (2.4) видно, что давление р_о, действующее на свободной поверхности жидкости, будет передаваться в любую точку внутри жидкости по всем направлениям одинаково (последнее утверждение вытекает из свойства гидростатического давления). Это позволяет сформулировать закон Паскаля: давление, приложенное к жидкости, передается по всем направлениям без изменения. Величину ρhg называют весовым давлением, т.к. она равна весу столба жидкости при единичной площади и высоте h.

Основное уравнение гидростатики можно записать иначе. Пусть необходимо определить давление р в точке М на уровне z (рис. 2.3). Подставив в уравнение (2.4) значение высоты h = z_о – z, получим: р = р_о + ρg (z_о – z).

После несложных преобразований получим основное уравнение гидростатики для двух точек одного и того же объема покоящейся жидкости:

z₀ + = z + . (2.5)

Поскольку точка М взята произвольно, то можно утверждать, что для всего рассматриваемого неподвижного объема жидкости:

z + = const. (2.6)

Таким образом, по формуле (2.4) в покоящейся жидкости в точке, находящейся на глубине h под свободной поверхностью, давление равно сумме внешнего давления р_о и весового давления ρhg.

2.3. Геометрическая интерпретация основного уравнения гидростатики. Избыточное, вакуумметрическое и абсолютное давление. Измерение давления.

Координата z рассматриваемой точки М жидкости (рис.2.3) отсчитывается от произвольной горизонтальной плоскости ОО, принятой в качестве координатной. В гидравлике эту плоскость называют плоскостью сравнения, а отсчитываемую от нее координату z точки – геометрической высотой.

Величина имеет линейную размерность и называется пьезо-

метрической высотой. Сумма z + называется гидростатическим

напором.

Если давление на свободной поверхности жидкости равно атмосферному, то плоскость пьезометрического напора совпадает со свободной поверхностью жидкости. При р_о ≠ р_атположения плоскости пьезометрического напора могут быть различными в зависимости от соотношения р_о > р_ат или р_о < р_ат.

Рассмотрим случай, когда давление в сосуде р_о > р_ат . Простейшим прибором жидкостного типа для измерения величины гидростатического давления является пьезометр, который представляет собой стеклянную трубку небольшого диаметра, открытую с одного конца и вторым концом присоединенную к сосуду, в котором необходимо измерить давление (рис.2.4).

Согласно основному уравнению гидростатики (2.4), давление в точке М будет равно:

р_м = р_о + ρgh = р_ат + ρgH,

откуда р_о = р_ат + ρg(H-h). (2.7)

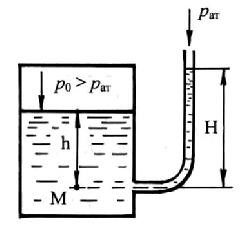
Рис. 2.4. Схема измерения избыточного давления пьезометром

Давление р_о, определенное с учетом атмосферного давления, называется абсолютным давлением (2.7).

Давление р_о, действующее на свободной поверхности жидкости в сосуде, превышает атмосферное давление на величину ρg (H-h).Это давление называется избыточным давлением (2.8):

р_изб = р_о - р_ат = ρg (H-h). (2.8)

Недостаток до атмосферного давления называется вакуумметрическим давлением (2.9).

Взаимосвязь между абсолютным, избыточным и вакуумметрическим давлением изображена на рис.2.5 (а и б).

Рис. 2.5. Взаимосвязь между давлением:

а) – абсолютным и избыточным; б) абсолютным и вакуумметрическим

Рассмотрим случай, когда давление внутри сосуда меньше атмосферного (рис.2.6).

Гидростатическое давление в точке М равно: р_м = р_о + ρgh = р_ат + ρgH.

Принимая во внимание, что h>H, получаем: р_о = р_ат - ρg (h-H).

Обозначим h_вак= h - H, тогда:

р_о = р_ат - ρgh_вак = р_ат - р_вак .

р_вак = - ρg h_вак< 0. (2.9)

^вак

Высоту h_вак, равную h_вак = , называют вакуумметрической высо

той.

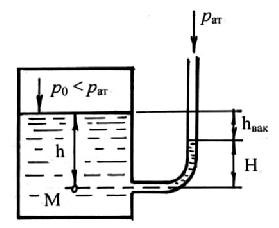
2.6. Схема для определения вакуумметрического давления

Измерения по пьезометру проводят в единицах длины, поэтому иногда давление выражают в единицах столба определенной жидкости. Рассмотрим схему, изображенную на рис.2.7.

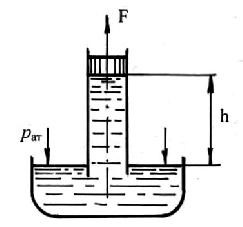
Рис.2.7. Всасывание жидкости поршнем

В трубке, нижний конец которой находится в жидкости, плотно подогнанный поршень постепенно поднимается вверх. Жидкость вслед за поршнем поднимается на некоторую высоту h от свободной поверхности, на которую действует атмосферное давление. Жидкость будет подниматься до тех пор, пока весовое давление столба жидкости не уравновесит атмосферное:

р_ат = ρgh = γh, (2.10)

^атоткуда h_мах = .

При нормальном атмосферном давлении (0,1053 МПа) высота h_мах равна: для воды – 10,33 м; для бензина (ρ = 750 кг/м³ ) – 13,8 м; для ртути – 760 мм.

Итак, атмосферное давление, равное 760 мм. рт. ст., соответствует высоте ртутного столба, равном 760 мм. Подставив это значение в уравнение (2.7) при ρ_рт = 13600 кг/м³, получим атмосферное давление, равное 1,013· 10⁵Па. Эта величина называется физической атмосферой. Она отличается от технической атмосферы, которая составляет 736 мм. рт. ст. (техническая атмосфера равна давлению, возникающему при действии силы в 1кгс на площадь размером 1см³:

1 ат =1 кгс/см²).

Ртутные манометры. Пьезометр является очень чувствительным и точным прибором, однако он удобен для измерения небольших давлений; при больших давлениях трубка пьезометра получается чрезмерно длинной. В этих случаях применяют жидкостные манометры, в которых давление уравновешивается жидкостью большего удельного веса. Обычно такой жидкостью является ртуть (рис.2.8).

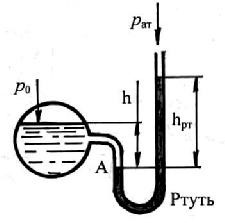
Рис. 2.8. Схема ртутного манометра.

По основному уравнению гидростатики (2.4):

р_а = р_о + γ₁h₁= р_ат + γ_ртh_рт,

откуда р_о = р_ат - γ₁h₁+ γ_ртh_рт.

В тех случаях, когда необходимо измерить не давление в сосуде, а разность давлений в двух сосудах или же в двух точках жидкости в одном и том же сосуде, применяют дифференциальные манометры

(рис.2.9).

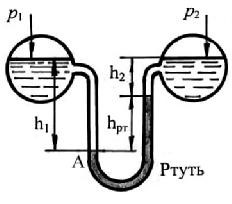
Рис. 2.9. Дифференциальный манометр

По основному закону гидростатики для точки А:

р_а = р₁ + γh₁= р₂ + γh₂+ γ_ртh_рт.

Разность давлений

р₁ - р₂ = γ (h₁- h₂) + γ_ртh_рт.

Для измерения давления вакуума ртутные манометры (вакуумметры) принципиально ничем не отличаются от обычных

(рис.2.10).

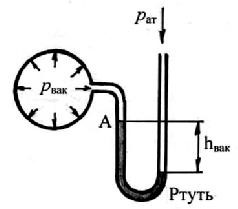
Рис. 2.10. Схема вакуумметра

В этом случае р_а = р_вак + γ_ртh_рт= р_ат,

рвак = γртhрт рат - γртhрт .

Для измерения давлений более 0,2 – 0,3 МПа применяют механические манометры - пружинные или мембранные. Наряду с механическими применяют и электрические манометры.

2.4. Относительный покой (равновесие жидкости в движущемся сосуде).

При равновесии в движущемся сосуде жидкость движется вместе с сосудом как единое целое, т.е. находится в состоянии относительного покоя. В этом случае на жидкость кроме массовой силы (силы тяжести) действует вторая массовая сила – сила инерции переносного движения.

Возможны два случая относительного покоя жидкости: в сосуде, движущемся прямолинейно и равноускоренно; и в сосуде, вращающемся вокруг вертикальной оси с постоянной угловой скоростью. В обоих случаях поверхности уровня, т.е. поверхности равного давления (в том числе и свободная поверхность жидкости) принимают такой вид, при котором равнодействующая массовая сила нормальна к этим поверхностям во всех их точках.

Анализ относительного покоя удобно проводить для сил, действующих на условную частицу жидкости с единичной массой. Таким образом, на каждую частицу жидкости с массой m =1 действуют сила тяжести G = g и сила инерции F_ин = a.

Прямолинейное движение. Рассмотрим сосуд, движущийся прямолинейно и горизонтально с постоянным ускорением (или замедлением) а (рис.2.11).

Равнодействующая единичных силы тяжести g и силы инерции а нормальна по отношению к свободной поверхности и будет равна:

= + .

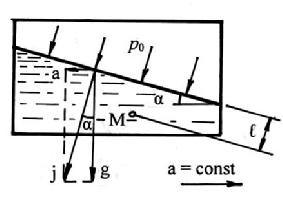
Рис. 2.11. Схема действия сил при прямолинейном движении сосуда

Уравнение, позволяющее находить давление в лютой точке рассматриваемого объема жидкости (например, в точке М), можно получить аналогично тому, как это сделано в п.2.2.

Давление в произвольной точке М на расстоянии ℓ от свободной поверхности будет равно: р_м= р_o + ℓ g j.

Это уравнение является частным случаем основного уравнения гидростатики. Действительно, при а = 0 следует, что j = g. Тогда с учетом ℓ = h получаем формулу (2.4), то есть основной закон гидростатики.

Цилиндрический сосуд, вращающийся относительно вертикальной оси. Рассмотрим цилиндрический сосуд радиусом R, вращающийся с постоянной угловой скоростью ω (рис.2.12).

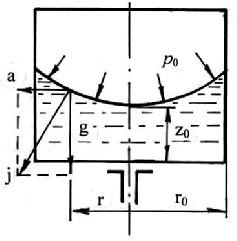
Рис. 2.12. Схема действия сил при вращении сосуда (общий случай)

Уравнение поверхности уровня (в частности, свободной поверхности жидкости в сосуде) в цилиндрических координатах (r_o,z₀) имеет вид:

z = z_o+^²
² , (2.11)

где z_o– вертикальная координата вершины параболы (высота жидкости на оси вращения), r, z – координаты любой точки поверхности уровня.

Формула для определения давления (например в точке М) в любой точке жидкости, находящейся в относительном покое, будет выглядеть так:

р = р_о + [(z_o – z) +^{² ²}]ρg. (2.12)

Если принять ω = 0 и обозначить h = z_o – z, то можно получить основной закон гидростатики (2.4).

На практике часто встречается другой случай – вращение сосуда с очень высокой скоростью (например, центрифуга). В этом случае центробежные силы гораздо больше сил тяжести и жидкость отбрасывается центробежными силами к стенкам сосуда, а ее свободная поверхность располагается на радиусе r_o (рис.2.13).

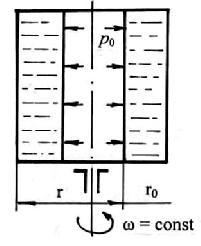
Рис. 2.13. Схема положения жидкости при вращении сосуда

Тогда формула для определения давления примет вид:

²( ₀²)

р = р_о + ρ. (2.13)

Повышение давления в жидкости, возникающее вследствие ее вращения, равно:

р = р_о + ^²ρ. (2.14)

2.5. Примеры.

При решении задач по гидростатике необходимо различать такие понятия, как давление р и сила F.

Применяя основное уравнение гидростатики нужно помнить, что второй член в правой части уравнения может быть как положительным, так и отрицательным. Необходимо также твердо различать давления абсолютное, избыточное и вакуумметрическое, а также весовое давление жидкости.

При решении задач, в которых даны поршни или системы поршней, следует писать уравнение равновесия, то есть равенство нулю суммы всех сил, действующих на поршень или систему поршней. В задачах на относительный покой жидкости следует учитывать повышение давления за счет силы инерции переносного движения.

2.5.1. В цилиндрический бак диаметром 2 м до уровня Н = 1,5 м налиты вода и бензин. Уровень воды в пьезометре ниже уровня бензина на h = 300 мм. Определить вес находящегося в баке бензина, если ρ_б= 700 кг/м³.

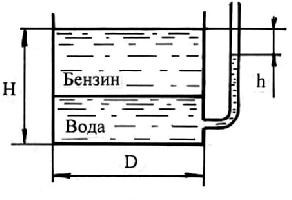
Весовое (избыточное) давление воды и бензина в баке будет равно весовому давлению воды в пьезометре:

ρ_вgh_в + ρ_бgh_б= ρ_вg(H – h).

Поскольку в этом уравнении есть два неизвестных, выразим h_в = H – h_б, и подставим:

ρ_вg (H – h_б) + ρ_бgh_б= ρ_вg (H – h). После сокращения получим:

h_б(ρ_в – ρ_б)= ρ_вh. Высота бензина в баке:

hб = в = · , = 1м. в б

Вес находящегося в баке бензина:

G = Mg = ρ_б·g·S·h_б= ρ_б·g·π·R²·h_б= 700·9,8·3,14·1² ·1= 21,54 кН.

2.5.2. Определить давление р_oвоздуха в напорном баке по показанию ртутного манометра. Какой высоты Н должен быть пьезометр для измерения того же давления р_o? Высоты h=2,6 м; h₁=1,8 м; h₂=0,6 м. Плотность ртути ρ= 13600 кг/м³, воды ρ= 1000 кг/м³.

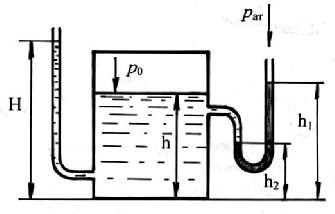
Абсолютное давление в баке на уровне высоты h₂будет равно абсолютному давлению в ртутном манометре на том же уровне: р_а = р_о +ρ_вg (h – h₂)= р_ат +ρ_ртg(h₁ – h₂).

р_o = р_ат +ρ_ртg(h₁ – h₂) - ρ_вg (h - h₂) = 100000 + 13600·9,8·1,2 – 1000·9,8·2= = 240,3 кПа.

Для нахождения высоты Н рассуждения аналогичны: р_ат +ρ_вg Н = р_о +ρ_вg h,

откуда Н = в ат = · , · , = 16,92 м.

в · ,

2.5.3. Определить силу F, действующую на шток гибкой диафрагмы, если ее диаметр D = 200 мм, показания вакуумметра р_вак= 0,05 МПа, высота h = 1 м. Площадью штока пренебречь. Найти абсолютное давление в левой полости, если h_a = 740 мм. рт. ст.

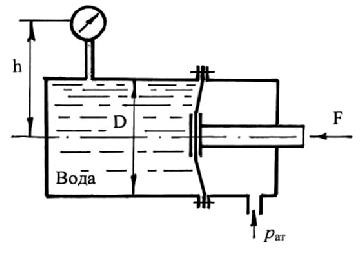
Действующее на шток диафрагмы давление вакуума определяется по показанию вакуумметра с учетом высоты столба воды h: р_вак.д. = ρgh – р_вак=1000·9,8·1 – 50000 = – 40200 Па.

Знак "–" указывает на то, что давление в левой полости гидроцилиндра по оси штока ниже атмосферного (давление вакуума). Атмосферное давление составляет:

р_ат = 740·133,3 = 98642 Па.

Абсолютное давление в левой полости (давление с учетом атмосферного давления):

р_аб = р_ат – р_вак.д. = 98642 – 40200 = 58442 Па. Сила, действующая на шток диафрагмы, равна:

F = рвак · ² = 40200 · , · , ² = 1,26 H.

2.5.4. Система из двух поршней, соединенных штоком, находится в равновесии. Определить силу, сжимающую пружину. Жидкость, находящаяся между поршнями и в бачке – масло с плотностью ρ = 870 кг/м³. Диаметры D =80 мм; d = 30 мм; высота Н = 1000 мм; избыточное давление р₀ = 10 кПа.

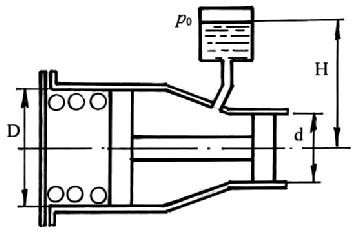
Избыточное давление, действующее на кольцевую поверхность поршней, будет равно:

р_изб = р₀ + ρgН = 10 000 + 870·9,8·1 = 18,5 кПа.

Силы, действующие на кольцевые площади поршней с диаметрами D =80 мм и d = 30 мм, будут равны:

₁ − d_ш).

F = р_изб (D

₁ − d_ш).

F = р_изб (d

Сила, сжимающая пружину, будет равна:

F = F₁ – F₂ = р_изб (D− d) = 18 500·^, ·(0,08² – 0,03²) = 79,87 Н.

2.5.5. Определить силу F, необходимую для удержания в равновесии поршня, если труба под поршнем заполнена водой, а размеры трубы: D =100 мм; Н = 0,5 м; h = 4м. Длины рычага: а = 0,2 м и b =1 м. Собственным весом поршня пренебречь.

Логично предположить, что сила F, необходимая для удержания поршня в равновесии, должна соответствовать давлению под ним, то есть весовому давлению столба жидкости:

р = ρg(Н + h) = 1000·9,8·(0,5 + 4) = 44,1 кПа.

Сила F в соответствии с длинами плеч рычага равна:

² , , · , ²

F = р = ·44 100· = 69,2 Н.

2.5.6. Топливный бак автомобиля длиной L = 0,6 м, шириной b = 0,5 м и высотой Н = 0,2 м движется с ускорением а = 3,27 м/с². Определить минимальное количество топлива в баке, обеспечивающее его подачу без подсоса воздуха. Считать, что бензопровод установлен в центре горизонтальной проекции бака, его диаметр мал по сравнению с длиной бака, высота h = 10 мм.

Изобразим положение бензина в баке с минимальным объемом.

Обозначим стороны прямоугольного треугольника как ℓ и у. Тогда:

, tg α = = = 0,33367.

х = = = 0,03 м. ,

ℓ = х + = 0,03 + ^, = 0,33 м

у = ℓ tg α = 0,33·0,33367 = 0,11 м.

Объем минимального количества бензина в баке, обеспечивающего его подачу без подсоса, будет равно: ℓу , · ,

W =Sb = b = ·0,5 = 9,1 л.

2.5.7. На рисунке показан элемент одной из возможных схем гидроусилителя сцепления автомобиля (трактора). Масло под давлением р₀ = 0,5 МПа подводится внутри вала и затем через отверстие – в полость между двумя совместно вращающимися цилиндром А и поршнем Б, который может скользить вдоль вала. Давление масла, увеличенное благодаря действию центробежных сил, заставляет поршень перемещаться вправо и обеспечивает этим силу нажатия, необходимую для включения сцепления. Определить силу давления масла на поршень Б, если его диаметр D =120 мм; диаметр вала d = 20 мм; частота вращения n = 6 000 об/мин; плотность жидкости ρ = 920 кг/м³.

Определим угловую частоту вращения:

· , · ω = = = 628 рад/с.

Увеличение давления за счет центробежной силы (уравнение 2.14) будет увеличиваться пропорционально увеличению расстояния от центральной оси элемента. В этом случае за увеличение давления примем его среднее значение:

= · ·( , , ) =335,62 кПа.

∆р = 2

Давление в полости элемента с учетом увеличения давления за счет действия центробежной силы будет равно: р = р₀ + ∆р = 500 000 + 335 620 = 835, 62 кПа.

Тогда сила, с которой действует давление р на поршень, будет равна:

^{2 2} , ^{2 2}

F = р (D + d ) = 835 620· ·(0,12 – 0,02 ) = 9,2 кН.

2.5.8. В сосуд высотой Н = 0,3 м залита жидкость до уровня h = 0,2м. Определить, до какой угловой скорости можно раскрутить сосуд, с тем, чтобы жидкость не выплеснулась из него, если диаметр сосуда D = 100 мм.

Уравнение свободной поверхности жидкости имеет вид (2.11):

Н = z₀ + ,

где z₀ – вертикальная координата вершины параболоида. Объем параболоида вращения W_п равен:

²(Н – z₀). W_п = πR

Выразим объем жидкости W_ж, находящейся в сосуде объемом W_с, учитывая объем параболоида W_п:

W_ж = W_с – W_п = Н – 2(Н – z0) = (Н + z0). πR

Поскольку можно вычислить объем жидкости W_ж в сосуде, находящегося в состоянии покоя, то можно записать:

h = (Н + z₀).

z₀= 2h – Н.

Угловую скорость ω можно выразить из уравнения свободной поверхности жидкости в сосуде (2.11):

ω = (Н ) = ( , , )· · , , = 39,6 рад/с.

2.5.7. Контрольные вопросы.

1. Дайте определение гидростатического давления.

2. Почему гидростатическое давление является функцией координат р = f(x,y,z)?

3. Что такое весовое давление жидкости?

4. Может ли давление в жидкости быть меньше нуля, равно нулю?

5. В каких случаях плоскость пъезометрического напора располагается выше или ниже свободной поверхности покоящейся жидкости? 6. Что такое абсолютное, избыточное и вакуумметрическое давление?

7. Как можно измерить атмосферное давление? В чем разница между физической и технической атмосферой?

8. Может ли движущаяся жидкость находиться в состоянии покоя?

Если может, то при каких условиях?

Раздел 3 Кинематика жидкости

Кинематика жидкости – это раздел гидромеханики (механики жидкости), в котором изучают виды и кинематические характеристики движений жидкости, но не рассматривают силы, под действием которых происходит движение.

3.1. Основные понятия и определения.

Как уже отмечалось в п. 1.1, жидкость рассматривают как сплошную среду, непрерывно заполняющую пространство без пустот и разрывов. Кроме того, для упрощения изучения движения жидкости используется так называемая "идеальная" жидкость (п. 1.3). Происходящие явления исследуют применительно к идеальной жидкости, а затем полученные закономерности переносятся с введением корректирующих поправок на потоки реальных жидкостей.

Движение жидкости можно считать определенным, если известны законы движения всех частиц.

Выделим в некоторой области жидкости произвольную частицу, которая с течением времени пройдет через ряд точек пространства, обладая при этом различными скоростями (рис. 3.1).

Рис. 3.1. Траектория движения частицы жидкости

Геометрическая линия, соединяющая последовательные положения движущейся частицы жидкости, представляет собой ее траекторию.

Рассмотрим некоторое пространство, заполненное движущейся жидкостью, которая состоит из отдельных частиц. В данный момент времени в каждой точке этого пространства, определяемой координатами (х, у, z), находится частица жидкости, имеющая некоторую скорость u. Эту скорость называют мгновенной местной скоростью. Совокупность мгновенных местных скоростей представляет собой векторное поле, называемое полем скоростей. В общем случае оно изменяется по времени и по координатам: u = ƒ (х, у, z, t).

Векторными линиями поля скоростей являются линии тока.

В некоторой части пространства, заполненного движущейся жидкостью, в произвольной точке 1 построим вектор скорости υ_А, изображающий (по величине и по направлению) скорость частицы жидкости А, находящейся в данный момент времени в этой точке. На этом векторе, на весьма малом расстоянии от первой точки, возьмем точку В и построим вектор υ_В, соответствующий скорости частицы в этой точке в тот же момент времени. На векторе υ_В возьмем точку С, отложим от нее вектор скорости υ_С и т. д. В результате получим ломаную линию АВСДЕ, стороны которой совпадают с направлениями векторов скоростей частиц жидкости А, В, С, Д и Е в данный момент времени (рис. 3.2).

Рис. 3.2. Линия тока

Если безгранично уменьшать длины отрезков АВ, ВС, СД, ДЕ и т. д., то в пределе ломаная линия превратиться в некоторую кривую линию, называемую линией тока.

Линия тока – это кривая, проведенная через ряд точек в движущейся жидкости таким образом, что векторы мгновенных местных скоростей частиц жидкости, находящихся в данный момент времени в этих точках, являются к ней касательными.

Необходимо иметь в виду различие между траекторией частицы жидкости и линией тока. В то время как траектория относится к одной определенной частице жидкости и показывает путь, проходимый этой частицей в пространстве за некоторый промежуток времени, линия тока связывает между собой различные лежащие на ней частицы и характеризует направление их движения в данный момент времени.

Движения жидкости по характеру изменения во времени поля скоростей делят на установившееся и неустановившееся.

Установившееся (стационарное) движение – это движение, когда в каждой точке области, где движется жидкость, местные скорости во времени не изменяются: u = ƒ(х, у, z,).

При установившемся движении линии тока и траектории движения частиц жидкости совпадают.

Неустановившемся движением называют течение жидкости, когда в точках области, где движется жидкость, местные скорости изменяются с течением времени и его описывают уравнением u = ƒ(х, у, z, t).

При неустановившемся движении линии тока и траектории частиц не совпадают. Линии тока соответствуют только мгновенному состоянию поля скоростей.

Выделим в жидкости элементарный (бесконечно малый) контур abcd, и через все его точки проведем линии тока, то образуется трубчатая поверхность, называемая трубкой тока (рис. 3.3).

Рис. 3.3. Трубка тока

При установившемся движении жидкости трубка тока обладает следующими свойствами:

- форма трубки тока неизменна во времени;

-жидкость течет внутри трубки, не пересекая ее поверхность, т. к. линии тока и траектории движения частиц совпадают.

Жидкость, движущаяся внутри такой трубки тока, образует элементарную струйку.

Ввиду малого поперечного сечения элементарной струйки местные скорости в его пределах можно считать одинаковыми, вдоль же струйки (по ее длине) скорость и поперечное сечение изменяется. Совокупность таких элементарных струек образует поток жидкости.

Скорости движения различных струек, из которых складывается поток, различны. Таким образом, поток жидкости рассматривается состоящим из отдельных элементарных струек, движущихся с различными скоростями.

При неустановившемся движении в связи с изменяемостью поля скоростей во времени струйки являются только мгновенными, т. к. трубки тока непрерывно изменяются.

Живым сечением потока (струйки), или просто сечением потока (струйки), называется сечение, нормальное в каждой своей точке к линиям тока. Например, поверхность, ограниченная контуром abcd (рис. 3.3), является сечением для элементарной струйки в пределах трубки тока, проведенной через этот контур. При параллельноструйном течении сечения представляют собой плоскости, перпендикулярные к направлению движения жидкости.

3.2. Расход. Уравнение расхода.

Расходом Q струйки называют объем жидкости, проходящий через данное живое сечение в единицу времени. Для элементарной струйки с равномерным распределением местных скоростей u по живому сечению площадью dS:

dQ = u · dS. (3.1)

Расход потока равен сумме расходов элементарных струек, составляющих поток:

Q =u · dS. (3.2)

Для потока реальной жидкости местные скорости в различных точках живого сечения будут различны. Вследствие наличия сил внутреннего трения скорость частиц жидкости в живом сечении потока будет возрастать по мере удаления от ограничивающей твердой поверхности.

Пусть существует условный поток, все точки живого сечения которого характеризуются одними и теми же местными скоростями, равными средней скорости в данном живом сечении. Тогда, умножив площадь живого сечения S на среднюю скорость в данном живом сечении, получим действительный расход жидкости, проходящий через это живое сечение:

Q = υ_ср· S. (3.3)

Средняя скорость в сечении представляет собой одинаковую для всех точек сечения воображаемую скорость, при которой через данное живое сечение проходит тот же расход, что и при действительных местных скоростях, разных в различных точках сечения.

Расход можно измерять в единицах объема, массы или веса. Поэтому различают объемный Q (м₃/с), массовый Q_m (кг/с), и весовой Q_G (Н/с) расходы. Между этими расходами существует такая же связь, как и между объемом, массой и весом. При расчете гидравлических систем обычно пользуются объемным расходом Q.

Уравнение расхода. Рассмотрим установившееся движение жидкости, причем внутри жидкости не возникает пустот, т. е. будем считать, что соблюдается условие сплошности или неразрывности движения.

Выделим сечениями 1-1 и 2-2 некоторый отсек элементарной струйки (рис. 3.4).

В этот отсек в единицу времени через сечение 1-1 втекает объем жидкости, равный u₁· dS₁. Через сечение 2-2 из него же вытечет объем u₂· dS₂.

Учитывая, что форма элементарной струйки не изменяется и поперечный приток или отток из нее отсутствуют, приходим к выводу, что элементарные расходы жидкости, проходящие через сечения 1-1 и 2-2, должны быть одинаковы:

dQ = u₁· dS₁ = u₂· dS₂ = …. = u_n· dS_n =const. (3.4)

Уравнение (3.4) называется уравнением расхода для элементарной струйки.

Рис. 3.4 Схема для вывода уравнения расхода.

Аналогичное уравнение можно составить и для потока реальной жидкости, используя понятие средней скорости:

Q = υ_ср₁· dS₁ = υ_ср₂· dS₂ = …. = υ_ср.
n· dS_n = const. (3.5)

Из уравнения (3.5) следует, что средние скорости в поперечных сечениях потока при условии неразрывности движения обратно пропорциональны площадям этих сечений: ^ср

⁼ . (3.6)

ср

Уравнение расхода является законом сохранения вещества для потока (струйки) жидкости, записанное при условии постоянства плотности жидкости в пределах рассматриваемого потока

(струйки).

3.3. Потоки жидкости.

Классификация потоков по характеру границ. В гидравлике потоком жидкости называют движущуюся массу жидкости, ограниченную направляющими твердыми поверхностями, поверхностями раздела жидкостей или свободными поверхностями. В зависимости от характера и сочетания ограничивающих поток поверхностей потоки делят на безнапорные, напорные и гидравлические струи.

Безнапорные потоки ограничены частично твердой, частично свободной поверхностью. Примером таких потоков может служить поток в реке или канале, а также в трубе, работающей неполным сечением.

Напорные потоки ограничены твердыми поверхностями по всему сечению, и гидродинамическое давление в любой точке потока отлично от атмосферного.

Гидравлические струи ограничены только жидкостью или газовой средой. Например, струя воды, вытекающая из сосуда через отверстие в атмосферу.

Гидравлические элементы потока. К ним относятся смоченный периметр и гидравлический радиус.

Смоченный периметр χ представляет собой длину линии, по которой жидкость в живом сечении соприкасается с твердыми поверхностями, ограничивающими поток. В напорных потоках длина смоченного периметра равна длине всего периметра сечения, а в безнапорных потоках – составляет некоторую часть полного периметра.

Гидравлическим радиусом R называют отношение площади живого сечения потока к смоченному периметру в этом сечении: R = S χ .

В напорном потоке для круглого сечения диаметром d и радиусом r имеем:

R = πd 4 d = d 4 = r 2 .

В безнапорном потоке для прямоугольного живого сечения с шириной b и глубиной жидкости h гидравлический радиус равен: R = bh b + 2h .

В достаточно широких потоках при малом значении отношения ^h b гидравлический радиус часто принимают равным глубине наполнения.

3.4. Примеры.

3.4.1. Труба, по которой течет вода, имеет переменное сечение. Определить скорость во втором сечении, если скорость в первом сечении υ₁=0,05 м/с; d₁=0,2 м; d₂=0,1м.

Из уравнения неразрывности потока (3.5) следует:

υ₂= υ₁ = υ₁ = 0,05 _, = 0,2 м/с.

3.4.2. По трубопроводу диаметром d = 150 мм перекачивается нефть плотностью ρ = 800 кг/м³ в количестве 1200 т. в сутки. Определить секундный объемный расход нефти Q и среднюю скорость ее течения υ.

Предварительно находим секундный массовый расход:

Q_m = = 13,9 кг/с.

Следовательно, секундный объемный расход равен:

Q =Q ρ = , = 17,37 л/с.

Далее по уравнению расхода (3.5):

υ = Q S = Q πd² = , · , · , = 0,98 м/с.

3.4.3. По полностью затопленному трубопроводу перекачивается жидкость со скоростью υ = 0,2 м/с. Определить расход жидкости Q, если гидравлический радиус R = 0,015 м.

Гидравлический радиус равен отношению площади живого сечения S = πr² и смоченного периметра χ = 2πr:

R =S = πr 2πr =r 2 .

Отсюда диаметр трубопровода d = 2r = 4R = 0,06 м.

Тогда расход жидкости:

² 3,14·0,06²

Q = υ · S = υ · = 0,2· ₄ =0,56 л/с.

3.4.4. Контрольные вопросы.

1. В чем разница между линией тока и траекторией? Могут ли они совпадать?

2. В чем различие установившегося и неустановившегося движения?

3. Что такое трубка тока, элементарная струйка жидкости?

4. Дайте определение живого сечения струйки, расхода жидкости и средней по живому сечению скорости.

5. Какой физический закон применительно к жидкости отражает уравнение неразрывности?

6. Каковы особенности безнапорных потоков, напорных потоков и гидравлических струй?

7. Что такое смоченный периметр и гидравлический радиус?

Раздел 4 Динамика жидкости

Динамика жидкости – это раздел гидромеханики, который изучает законы движения жидкостей в зависимости от приложенных к ним сил.

При заданных внешних силах задача динамики жидкости сводится к определению напряжений и кинематических параметров движения в каждой точке жидкости в любой момент времени, а также к определению гидродинамических сил воздействия потока на тела. 4.1 Уравнение Бернулли для элементарной струйки идеальной жидкости.

Выведем основное уравнение, связывающее между собой давление в жидкости и скорость ее движения.

Рассмотрим установившееся движение идеальной жидкости, находящейся под действием лишь одной массовой силы – силы тяжести. Выделим в элементарной струйке сечениями 1-1 и 2-2 участок произвольной длины; при этом площади этих сечений обозначим соответственно dS₁ и dS₂ (рис 4.1).

Рис. 4.1. Схема струйки идеальной жидкости

За бесконечно малый отрезок времени dt выделенный участок переместится в положение 1'-2'. Применим к движению данного участка идеальной жидкости теорему механики об изменении кинетической энергии, согласно которой изменение кинетической энергии тела равно работе сил, приложенных к телу.

Эта теорема может быть выражена следующим уравнением:

∆Е = ∑А , (4.1) где ∆Е – изменение кинетической энергии, ∑А – сумма работ действующих сил.

Работу за время dt по перемещению участка жидкости из положения 1-2 в положение 1'-2' совершают силы тяжести и силы давления. С учетом этого уравнение (4.1) примет вид:

∆Е = A_p + A_G, (4.2) где A_p - работа сил давления, A_G - работа сил тяжести.

Силы давления, действующие на выделенный участок струйки жидкости, складываются из сил давления на его боковую поверхность и на площади поперечных сечений dS₁ и dS₂.Работа сил давления на боковую поверхность равняется нулю, т. к. эти силы во все время движения нормальны к этой поверхности, следовательно, нормальны и к перемещению их точек приложения.

Сумма работ сил давления на поперечные сечения составит:

A_p = p₁dS₁u₁dt – p₂dS₂u₂dt, (4.3)

где p₁dS₁ и p₂dS₂ - силы гидростатического давления на поверхности сечений 1-1 и 2-2; u₁dt и u₂dt - элементарные перемещения этих поверхностей.

Работа силы давления на сечение 2-2 отрицательна, т. к. направление силы p₂dS₂ противоположно перемещению u₂dt.

Работа силы тяжести равна изменению потенциальной энергии положения участка струйки, то есть из энергии положения жидкости в объеме 1-2 нужно вычесть энергию положения жидкости в объеме 1'-2'. При этом энергия положения промежуточного объема 1'-2 сократится, и можно считать этот объем условно неподвижным. Тогда останется лишь разность энергий положения между объемами жидкости 1-1' и 2-2'. Центрами тяжести объемов 1-1' и 2-2' будут являться высоты соответственно z₁ и z₂. Если учесть уравнение расхода (3.5), то можно сделать вывод, что объемы, а следовательно и силы тяжести элементов 1-1' и 2-2' равны между собой. Тогда работа силы тяжести выразится как произведение разности высот z₁ и z₂на силу тяжести dG:

A_G = (z₁ – z₂) dG. (4.4)

Кинетическая энергия тела с массой m будет равна:

^mu 2 = ^Gu 2g . (4.5)

E_к =

Приращение кинетической энергии ∆Е рассматриваемого участка струйки за время dt будет равно разности кинетических энергий объемов 1-2 и 1'-2'. При вычитании останется разность кинетических энергий элементов 2-2' и 1-1':

∆Е = ^dG 2g – ^u^dG 2g . (4.6) Подставив полученные выражения (4.3), (4.4) и (4.6) в уравнение (4.2), получим: p1dS1u1dt – p2dS2u2dt + (z1 – z2) dG = u dG 2g – u dG 2g .

Разделим это уравнение на dG = ρgυ₁dS₁dt = ρgυ₂dS₂dt, произведем сокращения и получим:

– + z1 – z2 = – .

Перегруппируем члены уравнения таким образом, что члены уравнения, относящиеся к первому сечению, будут находиться в левой части уравнения, а члены уравнения, относящиеся ко второму сечению – в правой:

z₁ + + = z₂ + + (4.7)

Уравнение (4.7) называют уравнением Бернулли для элементарной струйки идеальной несжимаемой жидкости. Оно было выведено Даниилом Бернулли, действительным членом Петербургской Академии наук в 1738 г. Термин "гидродинамика" впервые появился в книге Д. Бернулли, опубликованной в том же году.

Графическая иллюстрация уравнения Бернулли. Учитывая, что сечения 1-1 и 2-2 были взяты совершенно произвольно, то уравнение (4.7) можно применить в любом поперечном сечении струйки, взятом по ее длине, и представить в следующем виде:

z + + = Н = const. (4,8)

Сумма трех слагаемых, входящих в уравнение (4.8), называется полным напором в данном сечении струйки. Различают геометрический напор z, пъезометрический напор ρg и скоростной напор

^u 2g .

В соответствии с этим уравнение Бернулли можно сформулировать следующим образом: для элементарной струйки идеальной жидкости полный напор, то есть сумма геометрического, пъезометрического и скоростного напоров есть величина постоянная во всех сечениях струйки.

Величины напоров измеряются единицами длины. Величина z – это координата центра тяжести сечения струйки (измеряется в ρg ] = кН^г м_м ^м _с = м и метрах). Размерность величин [

м с

[

^u 2g ] =^м_с = м ─ линейная.

Это дает возможность представить уравнение Бернулли в графическом виде. По оси абсцисс откладывают расстояния по оси струйки от некоторого сечения, принимаемого за начальное, а по оси ординат - значения составляющих напора для ряда сечений струйки

(рис. 4.2).

Рис. 4.2. Графическая иллюстрация уравнения Бернулли для элементарной струйки идеальной жидкости.

Откладывая от плоскости сравнения ОО вертикальные отрезки z, ρg и ^u 2g , найдем геометрическое место концов сумм этих

отрезков, которое расположится на горизонтальной плоскости, поднятой над плоскостью сравнения на высоту Н. Эту плоскость в виде горизонтальной линии называют напорной линией. Соединив концы от-

резков z + ρg , получим пъезометрическую линию.

4.2. Энергетическая интерпритация уравнения Бернулли для установившегося движения.

Уравнение Бернулли выражает закон сохранения механической энергии в идеальной жидкости, поскольку каждый член уравнения (4.7) представляет собой определенный вид удельной энергии (энергии, отнесенный к единице веса жидкости).

Если принять плоскость сравнения за плоскость нулевой потенциальной энергии, то можно утверждать, что подняв массу жидкости m на высоту z, ей сообщили потенциальную энергию mgz. Отсюда следует, что высота z выражает потенциальную энергию, отнесенную к единице веса, которую называют удельной потенциальной энергией положения. Высоту z еще называют нивелирной высотой.

Отношение ρg представляет собой удельную энергию дав-

ления (сжатия) жидкости. Это отношение называется пъезометрической высотой.

Сумма величин z + ρg является удельной потенциальной

энергией жидкости. В гидравлике эта сумма называется гидростатическим напором.

Отношение ^u 2g представляет собой удельную кинетическую

энергию жидкости.

Энергетический смысл уравнения Бернулли можно сформулировать так: при движении идеальной жидкости ее полная удельная энергия есть величина постоянная вдоль всей струйки.

4.3. Уравнение Бернулли для потока реальной жидкости.

Получим уравнение Бернулли для потока реальной жидкости, основываясь на том, что оно является законом сохранения энергии для движущейся жидкости.

Полная удельная энергия потока реальной жидкости есть сумма удельной потенциальной и удельной кинетической энергий в данном сечении:

Е = Е_п + Е_к . (4,9)

При установившемся движении реальной жидкости давление по живому сечению распределяется согласно гидростатическому давлению, то есть:

Е_п = z + ρg = const. (4.10) Согласно этому утверждению, удельную потенциальную энергию потока Е_п можно определить в любой точке данного живого сечения, поскольку сумма (4.10) для всех точек этого сечения при рассматриваемом движении будет одинаковой.

При движении реальной жидкости скорости в сечении потока ввиду наличия сил вязкости будут различны (рис. 4.3).

Рис. 4.3. Схема потока реальной жидкости

Вычисление удельной кинетической энергии потока по средней скорости не отражает всей картины изменения скоростей по живому сечению. Поэтому сперва определим удельную кинетическую энергию потока по местной скорости u в данном сечении.

Удельную кинетическую энергию потока по местной скорости можно определить, разделив кинетическую энергию массы жидкости, проходящей через данное сечение в единицу времени, на ее вес.

Разобьем данное сечение на элементарные площадки dS с равными местными скоростями в пределах этих площадок. Тогда кинетическая энергия элементарной массы жидкости dm, протекающей через площадку dS с местной скоростью u, равна:

= dm = ρ · dQ = ρ · u · dS u . (4.11)

Е_к

Кинетическую энергию массы жидкости, протекающей в единицу времени через все живое сечение площадью S с местной скоростью u можно найти, проинтегрировав уравнение (4.11) по площади S:

Е к = u · dS u .

Тогда удельная кинетическая энергия будет равна:

Е_кu = ^· ^· = udS (4.12) Удельная кинетическая энергия потока жидкости, вычисленная по средней скорости υ_ср потока в живом сечении, будет равна:

Е_кυ = = .

Обозначим отношение Е_кu и Е_кυ через α:

^Е

α = ^к_Е_к, (4.13)

Е_кu = α Е_кυ .

Коэффициент α называют коэффициентом кинетической энергии или коэффициентом Кариолиса. Этот коэффициент учитывает неравномерность распределения скоростей частиц жидкости в сечении реального потока. Уравнение (4.13) отображает физический смысл коэффициента Кариолиса.

Таким образом, удельная кинетическая энергия потока в данном сечении может быть определена по средней скорости в этом сечении, если известен коэффициент Кариолиса α:

Е_к = ^αυ 2g . (4.14)

В таком виде удельная кинетическая энергия потока входит в уравнение Бернулли для потока реальной жидкости. Значение коэффициента α определяют экспериментально для различных видов движения жидкости. Его значение находится в пределах от 1 до 2.

Распространим на поток жидкости, ограниченный неподвижными границами (канал, трубопровод), уравнение Бернулли, выведенное для струйки (рис. 4.4).

Рис. 4.4. Графическое изображение уравнения Бернулли для потока реальной жидкости

Тогда полная удельная энергия потока для любого сечения (например, 1-1) согласно уравнению (4.9):

Е₁ = Е_п₁ + Е_к₁ = z₁ + + . (4.15)

Для потока реальной жидкости сумма удельной потенциальной и удельной кинетической энергий равна:

Н = z + + . (4.16)

Величину Н в уравнении (4.16) называют гидродинамическим напором.

При движении реальной жидкости на пути от сечения 1-1 до рассматриваемого сечения (например, 2-2 или 3-3), происходит потеря удельной энергии, затрачиваемой на преодоление сопротивлений.

Торможение потока происходит вследствие:

- действия сил молекулярного сцепления между жидкостью и стенкой, ограничивающий поток;

- возникновения касательных напряжений между слоями движущейся жидкости (влияние свойства вязкости);

- вращения частиц жидкости, вихреобразования и перемешивания.

Эти потери оценивают значением h_тр, то есть частью механической энергии, необратимо переходящей в тепловую.

Уравнение Бернулли для установившегося движения вязкой несжимаемой жидкости между двумя сечениями 1-1 и 2-2 имеет вид: z1 + + = z2 + + + hтр , (4.17)

где z₁ и z₂ –высоты положения центров тяжести выбранных сечений; α₁ и α₂ – коэффициенты Кариолиса в сечениях 1-1 и 2-2; υ₁ и υ₂ – средние скорости в рассматриваемых сечениях; h_тр– потери удельной энергии (напора) на участке между рассматриваемыми сечениями.

Схема к уравнению Бернулли представлена в приложении 1.

Уравнение Бернулли для потока реальной жидкости представляет собой уравнение баланса энергии с учетом потерь.

При движении реальной жидкости напорная линия представляет собой наклонную линию, т. к. удельная энергия потока уменьшается в направлении движения потока жидкости.

Гидравлическим уклоном J называется отношение потерь напора h_тр к длине участка ℓ, на котором эти потери происходят: h^тр . J =

Пъезометрический уклон равен:

Jп = ( Eп – Еп ) ℓ .

Уравнение Бернулли для потока жидкости при неустановившемся движении будет иметь вид:

z1 + + = z2 + + + hтр.н + hин,

где h_тр.н – потери напора при неустановившемся движении на участке между сечениями 1-1 и 2-2; h_ин – инерционный напор.

Инерционный напор не является мерой дополнительных потерь энергии, он выражает обратимые преобразования энергии: ℓ

h_ин = α' ,

где α' – коэффициент Буссинекса (коэффициент количества движения); ^dυ dt – градиент скорости; ℓ – рассматриваемый участок жидко-

сти.

Инерционный напор может быть как положительным, так и отрицательным. Если движение ускоренное (^dυ dt > 0), то h_ин > 0, а если замедленное (^dυ dt < 0), то h_ин < 0.

В практических расчетах обычно принимают потери удельной энергии при установившемся и при неустановившемся движении жидкости равными. Такое допущение связано с недостаточным объемом исследований, посвященных гидравлическому сопротивлению неустановившегося движения жидкости и недостоверностью данных о влиянии ускорений на потери удельной энергии.

4.4. Измерение расходов и скоростей жидкости.

Наиболее простыми и достаточно точными способами измерения расхода жидкости являются объемный и весовой способы.

При объемном способе измерения жидкость поступает в специальный мерный сосуд, время наполнения которого фиксируется по секундомеру. Если объем сосуда – W, а время его наполнения – t, то объемный расход будет равен Q =^W _t .

При весовом способе находят вес всей жидкости, поступившей в сосуд за время t, и зная плотность жидкости, определяют весовой расход как Q = G ρgt .

Однако объемный или весовой способы пригодны лишь при сравнительно небольших значения расхода жидкости. Поэтому в практике используют специальные приборы, которые предварительно тарируются объемным или весовым способом.

Водомер Вентури. Большим достоинством этого водомера является простота конструкции и отсутствие в нем каких – либо движущихся частей.

Трубчатые водомеры могут быть с горизонтальной или с вертикальной осью. Рассмотрим водомер с горизонтальной осью

(рис. 4.5).

Рис. 4.5. Схема расходомера Вентури

Скорость потока в суженом месте (сечение 2) возрастает, а давление падает. Возникает разность давлений, которая измеряется двумя пъезометрами.

Составим уравнение Бернулли для сечений 1-1 и 2-2, пренебрегая очень небольшими потерями между этими сечениями:

= + , откуда – = – . +

Поскольку – = h, то h = – .

Исходя из уравнения постоянства расхода , выразим скорость υ₁:

υ₁= υ₂ ,

где S₁ и S₂–площади сечений 1 и 2 с диаметрами d₁ и d₂.

Тогда перепад давлений в сечениях 1 и 2 будет равен:

[ ^S]

h = 1 – _S .

Средняя скорость в сечении 2 будет равна:

υ2 = = К .

Искомый расход жидкости будут равен:

Q = S₂ К .

В действительности ввиду неравномерности распределения скоростей в поперечных сечениях потока, а также за счет неизбежных потерь напора между рассматриваемыми сечениями, действительный расход жидкости будет несколько отличаться от вычисленного по этой формуле, что учитывается введением поправочного коэффициента n:

Q = n S₂ К .

При практическом определении расхода обычно пользуются формулой:

Q = с ,

где коэффициент с = nS₂К называется постоянной водомера и имеет для данного водомера вполне определенное значение.

Трубка Пито. В простейшем виде трубка Пито представляет собой изогнутую под прямым углом трубку небольшого диаметра, установленную в потоке открытым нижним концом навстречу течения жидкости; другой, верхний конец трубки, выводится наружу

(рис. 4.6).

Рис. 4.6 Схема трубки Пито для измерения скоростей жидкости

Если такую трубку установить в открытом потоке (например, в канале), где на свободной поверхности жидкости давление равно атмосферному, то высота h поднятия жидкости в трубке над поверхностью потока представит собой величину скоростного напора ^υ 2g в точке установки трубки h = ^υ 2g ; откуда и находится скорость

движения жидкости как υ = а 2gh , где а – поправочный коэффициент, учитывающий потери напора в самой трубке и некоторое нарушение потока, вызываемого размещением самой трубки.

Для доказательства запишем уравнение Бернулли для потока жидкости, причем плоскость сравнения расположим по оси трубки, то есть z = 0. Тогда для сечений 1 и 2:

+ = + h1-2 .

Скорость υ₂ частиц жидкости, попадающих в отверстие трубки, равна нулю, а следовательно давление увеличивается на величину скоростного напора. Поэтому высота h представляет собой полный напор в сечении 2:

h = + = .

Потери напора учтем в поправочном коэффициенте а, поэтому:

h = – = .

Трубка Пито – Прандтля. Применяется для измерения ско рости движения жидкости в напорных трубопроводах (рис. 4.7).

Рис. 4.7. Схема трубки Пито – Прандтля

Поскольку в трубке Пито высота поднятия жидкости представляет собой полный напор, а высота жидкости в пъезометре – пъезометрический напор, то разность высот уровней жидкости в двух трубках составит скоростной напор: h = ^υ 2g .

Обычным бытовым прибором для измерения расходов жидкости является водомер, основным элементом которого является вертушка. Вертушка представляет собой колесо с лопастями, установленное на валу. Будучи установлена в потоке, вертушка (крыльчатка) под воздействием протекающей жидкости вращается, причем число ее оборотов прямо пропорционально скорости течения.

4.5. Примеры.

При применении уравнения Бернулли важно правильно выбрать те два сечения, для которых оно записывается. В качестве сечений рекомендуется брать:

- свободную поверхность жидкости в резервуаре (баке), где скорость υ = 0;

- выход в атмосферу, где р_изб = 0; р_абс = р_ат. ;

- сечение, где присоединен тот или иной манометр, пъезометр или вакуумметр;

- неподвижный воздух вдалеке от входа в трубу, в которую происходит всасывание из атмосферы;

Уравнение Бернулли рекомендуется сначала записать в общем виде, а затем переписать с заменой его членов заданными буквенными величинами и исключить члены, равные нулю.

При этом необходимо помнить, что:

- вертикальная ордината z всегда отсчитывается от произвольно выбранной плоскости вверх;

- давление р, входящее в правую и левую части уравнения, должно быть задано в одной системе отсчета.

4.5.1. Из напорного бака вода течет по трубе диаметром d₁= 20 мм, и затем вытекает в атмосферу через насадок с диаметром выходного отверстия d₂ = 10 мм. Избыточное давление воздуха в баке р₀= 0,18 МПа; высота Н = 1,6 м. Пренебрегая потерями энергии, определить скорости течения воды в трубе υ₁ и на выходе из насадка.

В качестве сечений, для которых составим уравнение Бернулли, выберем свободную поверхность в резервуаре и сечение на выходе из насадка диаметром d₂. Тогда:

Н + ат + = 0 + ат + _.

Ввиду значительных размеров сосуда по сравнению с поперечными размерами трубопровода скорость υ₀ будет весьма мала и ею можно пренебречь, то есть υ₀ = 0.

= (Н + ) ·2g , откуда υ₂ = 2gН + . υ

₂ = 2 · 9,8 · 1,6 + = 19,8 м/с.

Из уравнения расхода (3.5) находим скорость υ₁:

υ1 = = = , · , , = 4,95 м/с.

4.5.2. Определить, на какую высоту поднимется вода в трубке, один конец которой присоединен к суженному сечению трубопровода, а другой конец опущен в воду. Расход воды в трубе Q = 0,025 м³ ⁄с; избыточное давление р₁ = 49 кПа; диаметры d₁ = 100 мм и d₂ = 50 мм.

Потерями напора пренебречь.

Уравнение Бернулли для сечений 1 и 2 относительно оси трубы при α₁ = α₂ = 1 имеет вид:

+ = + _.

Учитывая, что h_вак.= ρg , υ₁ = ^4Q πd и υ₂ = ^4Q πd , то

получим:

hвак. = + _d₁⁻_d₂

· · ,

hвак. = · , + · , · , , − , = – 2,76 м.

Полученная высота – вакуумметрическая высота. На эту высоту h_вак.= 2,76 м и поднимется вода в трубке.

4.5.3. Контрольные вопросы.

1. Что такое пъезометрический, скоростной и гидродинамический напор? Как они изменяются по длине (по направлению движения жидкости)?

2. Как ориентирована напорная линия при установившемся движении вязкой жидкости?

3. Почему уравнение Бернулли выражает закон сохранения механической энергии в жидкости?

4. Что называется полной удельной энергией потока?

5. Чем отличается уравнение Бернулли для идеальной жидкости от того же уравнения для реальной жидкости?

6. Поясните смысл коэффициента Кариолиса в уравнении Бернулли.

7. За счет чего происходит уменьшение удельной энергии потока?

8. Что такое пъезометрический и гидравлический уклон?

9. В каких измерительных приборах используются закономерности уравнения Бернулли?

10. В чем разница между трубкой Пито и трубкой Пито - Прандтля?

Раздел 5 Режимы движения жидкости Уравнения Рейнольдса

5.1. Основы гидродинамического подобия.

Как уже отмечалось выше, при изучении гидравлических явлений большая роль отводится экспериментальному исследованию (опыту), которое проводится в лабораторной обстановке на идеализированных моделях потоков. Для того, чтобы полученные результаты перенести на реальные потоки жидкости, необходимо знать законы соответствия между геометрическими размерами, кинематическими и динамическими характеристиками потоков в модели и реальности, то есть необходимо, чтобы потоки были подобны.

Для оценки степени подобия двух потоков используют так называемые критерии подобия – безразмерные величины, полученные теоретически и позволяющие рассчитать конкретную гидравлическую систему по модели.

Для геометрического подобия необходимо, чтобы отношение любых соответствующих линейных размеров рассматриваемых потоков было одним и тем же (рис. 5.1), то есть:

= = … =К_L = const.

Рис. 5.1. Схема подобия потоков І и ІІ

Коэффициент К_L выражает пропорциональность между линейными размерами обоих потоков и носит название линейного масштаба.

Кинематическое подобие подразумевает подобие скоростей в сходных точках, то есть отношение любой скорости в первом потоке к аналогичной скорости во втором потоке должно являться величиной постоянной и отражается коэффициентом подобия, называемым масштабом скорости:

І І

= = …= const.

ІІ ІІ

Таким образом, признаками кинематического подобия двух геометрически подобных потоков будут являться одинаковые законы распределения скоростей в сходных сечениях.

Для того, чтобы сравниваемые потоки были динамически подобны, необходимо, чтобы в соответствующих точках сравниваемых потоков были подобны действующие в них одноименные силы. Такими силами могут быть силы тяжести, силы инерции, силы внутреннего трения жидкости.

Оценку динамического подобия проводят, сравнивая различные силы в данном потоке с одной из сил, которую используют в качестве силы сравнения. За такую силу принимают силу инерции F_ин.

Наиболее важными для напорных потоков являются силы трения F_тр. Логично предположить, что отношение сил инерции и сил трения может служить критерием оценки динамического подобия двух потоков, для которых соблюдены условия геометрического и динамического подобия.

Поместим в поток жидкости пластину бесконечно малой толщины перпендикулярно направлению движения (рис. 5.2).

Рис. 5.2. Схема установки пластины поперек потока

Силу, с которой поток воздействует на эту пластину, будем считать пропорциональной F_ин. Как известно из теоретической механики, по основному уравнению динамики сила равняется произведению массы на ускорение:

F_ин = mа , (5.1)

где масса m есть плотность жидкости ρ, умноженная на ее объем ℓ³ (ℓ – условный геометрический размер).

m = ρℓ³ .

Ускорение определяется приращением скорости υ = ^ℓ _t в единицу времени t: а = ^υ _t = ^ℓ t .

Следовательно, F_ин будет равно:

F_ин = ρ·ℓ³·^ℓ t = ρ· ^ℓ t = ρ·υ²·ℓ² = ρ·υ²·S . (5.2)

Таким образом, сила инерции, с которой поток может воздействовать на неподвижную преграду, пропорциональна произведению плотности жидкости ρ, условной площади S и квадрату скорости υ².

Силу, с которой поток воздействует на пластину, установленную параллельно направлению потока (рис.5.3), будем считать пропорциональной силе трения F_тр.

Рис. 5.3. Схема установки пластины вдоль потока

Тогда сила трения F_тр будет пропорциональна произведению касательных напряжений и площади условной поверхности S:

F_тр = τ·S.

С учетом уравнений (1.10) и (1.13) выражение для F_тр примет вид:

F_тр= μS = νρS . (5.3) ℓ

Итак, критерием динамического подобия двух потоков будет являться отношение сил инерции F_ин к силам трения F_тр. Этот критерий называют числом Рейнольдса R_е:

^ин

R_е= . (5.4)

тр

Подставив зависимости (5.2) и (5.3) в уравнение (5.4), получим:

ρSυ ℓ

Rе = ρνS = .

При использовании полученной формулы для потоков жидкости, движущихся в круглых трубах, в качестве скорости берут среднюю скорость в сечении, а в качестве условного геометрического размера ℓ - внутренний диаметр трубы d. Тогда:

R_е= . (5.5)

В качестве условного геометрического размера ℓ принимают также гидравлический радиус R и глубину жидкости в открытом русле (канале) h:

ℓ

R_е= ; R_е= .

Кроме числа Рейнольдса в качестве критерия подобия движения жидкости существуют:

- число Эйлера, отражающее отношение силы давления и инерции Е_u = ∆ ρυ , где ∆р – некоторая разность давлений (или просто дав-

ление);

- число Фруда, отражающее отношение силы тяжести и силы инерции F_r =^υ gℓ , где ℓ – условный геометрический размер и т. д.

Таким образом, существует ряд безразмерных параметров (кроме перечисленных выше существуют число Вебера, учитывающее силы поверхностного натяжения; число Коши, учитывающее упругость жидкости; число Струхаля и число Кармана), которые характеризуют течение жидкости. Одновременное выполнение различных законов подобия в большинстве случаев практически неосуществимо. Поэтому при моделировании исходят только из того закона подобия, который в рассматриваемом случае имеет решающее значение.

Например, при моделировании большинства гидротехнических сооружений, истечения жидкости через водосливы, изучении волнового сопротивления (испытываемого движущимися кораблями) используют число Фруда, т. к. решающее значение в данном случае имеет сила тяжести. Если преобладающее значение имеет сила поверхностного натяжения (например, при истечении жидкости из капиллярных отверстий или при распылении топлива в двигателях), используют число Вебера и т. д.

5.2. Режимы течения жидкости.

Как уже отмечалось выше, для напорных потоков наиболее важное значение имеют силы внутреннего трения, характеризуемые числом Рейнольдса R_е. Этот критерий характеризует режимы течения жидкости в напорном трубопроводе.

Многочисленные экспериментальные исследования показали, что потери энергии при движении жидкости существенно зависят от особенностей движения частиц жидкости в потоке, то есть от режима движения жидкости.

Наглядно особенности режимов движения можно наблюдать на специальной опытной установке, схема которой изображена на рис. 5.4.

Рис. 5.4. Демонстрация режимов течения жидкости:

а – ламинарное течение; б – турбулентное течение

К баку Б достаточно больших размеров присоединена стеклянная труба Т, ее вход сделан плавным, в конце установлен кран К для регулирования расхода потока. Расход измеряют с помощью мерного бака М и секундомера (объемный способ измерения расхода).

Над баком Б расположен сосуд С, наполненный раствором краски, плотность которой близка к плотности жидкости в потоке. По трубке Т₁ краска вводится в жидкость, движущуюся по трубке Т. Расход краски регулируют краном Р.

При открытом кране К в трубе Т установится некоторая скорость потока (высота уровня жидкости в баке Б поддерживается постоянной). При открытии крана Р в трубу Т начнет поступать подкрашенная жидкость. При малой скорости потока υ в трубе Т краска образует прямолинейную и резко выделяющуюся, не смешивающуюся с движущимся потоком струйку жидкости. Это свидетельствует о том, что в прямой стеклянной трубе Т при данном открытии крана К жидкость движется отдельными, не перемешивающимися между собой слоями. Линии тока при этом прямолинейны и устойчивы (рис. 5.4, а).

При некотором большем открытии крана К происходит увеличение скорости движения жидкости в трубе Т, струйка подкрашенной жидкости начинает искривляться и становится волнообразной. Это может происходить только в результате пульсации (изменении во времени) векторов местных скоростей в потоке.

При дальнейшем увеличении скорости потока в трубе Т струйка распадается на отдельные, хорошо видные вихри и перемешивается со всей массой текущей жидкости (рис. 5.4, б).

Движение жидкости, при котором отсутствуют изменения (пульсации) местных скоростей, называют ламинарным (от латинского слова "lamina" – слой), а изменения (пульсации) местных скоростей, приводящие к перемешиванию жидкости – турбулентным (от латинского слова "turbulentus" – беспорядочный).

Безразмерный критерий R_е для характеристики режима движения жидкости ввел английский ученый О. Рейнольдс в 1883 г., позднее названный его именем.

Основными факторами, определяющими характер режима течения жидкости, как это видно из уравнения Рейнольдса (5.5), являются:

- средняя скорость движения жидкости υ_ср ;

- диаметр трубопровода d;

- плотность жидкости ρ;

- динамическая вязкость жидкости μ.

Результаты экспериментов показали, что разрушение ламинарного режима движения жидкости в круглых трубах начинается приблизительно при R_е = 2300. Таким образом, при R_е < 2300 наблюдается устойчивое ламинарное течение жидкости, при R_е > 2300 – устойчивое турбулентное течение.

Скорость потока, при которой меняется режим движения жидкости, называют критической.

Рейнольдсом было обнаружено существование двух критических скоростей:

- верхняя критическая скорость υ_кр.в(при переходе ламинарного режима в турбулентный);

- нижняя критическая скорость υ_кр.н(при переходе турбулентного режима в ламинарный).

В опытах самого Рейнольдса R_кр.н = 2000, R_кр.в= 12000, то есть при R_кр.н < R_е < R_{кр.в ,}наблюдается неустойчивое состояние потока.

В настоящее время при практических расчетах обычно принято исходить из значения R_е = 2300, то есть при меньших значениях числа Рейнольдса наблюдается ламинарный режим, при больших – турбулентный.

В природе и технике турбулентное движение жидкости наблюдается чаще, чем ламинарное. Турбулентное течение встречается в потоках маловязких жидкостей и в трубах с большими проходными сечениями. К ним относятся потоки в гидравлических системах для перекачки воды или жидкостей на водяной основе, бензина, керосина, а также потоки различных газов.

Области ламинарного движения – движение вязких жидкостей типа масел по трубам и в механизмах, движение грунтовых вод (но он может быть и турбулентным), движение в капиллярах (в том числе и движение крови в живых организмах).

5.3. Ламинарный режим движения жидкости.

Рассмотрим основные закономерности ламинарного режима при равномерном движении жидкости в круглых трубах, когда ось трубы горизонтальна.

Поскольку при ламинарном режиме имеет место слоистое движение жидкости без перемешивания, то будем считать, что в данном потоке скорости течения жидкости параллельны оси трубы и поперечные скорости отсутствуют.

Механизм движения жидкости при ламинарном режиме можно представить в виде телескопического выдвижения цилиндров разного диаметра послойно друг из друга (рис. 5.5). При этом скорость в слое, непосредственно соприкасающимся со стенками трубы вследствие наличия сил молекулярного взаимодействия, равняется нулю и достигает максимального значения в слое, движущемся по оси трубы.

Причем при поступлении жидкости в трубу распределение скоростей по сечению трубы получается практически равномерным (рис. 5.6). Затем под действием сил вязкости происходит перераспределение скоростей по сечениям. По мере удаления от входа (ввиду трения у стенок) прилегающие слои жидкости начинают затормаживаться. Так как количество протекающей жидкости остается неизменным, замедление движения в пограничном слое вызывает увеличение скорости в середине потока. Когда формирование потока заканчивается, кривая скоростей принимает параболическую форму.

Рис. 5.5. Схема ламинарного режима движения жидкости

Рис.5.6 Схема распределения скоростей по длине потока при ламинарном течении

Скорость в живом сечении сформированного потока (эпюра А) будет равна:

υ_м = 2υ_ср 1 − ^r . (5.6) r0

Математическая зависимость (5.6) имеет квадратичный характер, то есть эпюра распределения скоростей в сформировавшемся потоке является квадратичной параболой.

Зависимость (5.6) позволяет установить (при r = 0) соотношение между максимальной υ_max и средней υ_ср скоростями: υ_max = 2 υ_ср .

Зная закон распределения скоростей по сечению трубы, легко определить коэффициент Кариолиса, учитывающий неравномерность распределения скоростей по живому сечению в уравнении Бернулли для случая установившегося ламинарного течения жидкости в круглой трубе.

Для этого в выражении (4.13) заменим скорость по формуле (5.6). После математических преобразований можно получить численное значение коэффициента Кариолиса α_л = 2.

Входной участок трубы, на котором происходит формирование кривой скоростей, носит название начального участка ℓ_нач потока жидкости при ламинарном режиме движения: ℓ_нач = 0,028 R_еd.

Потери напора на трение на начальном участке трубы на 9% больше, чем потери в области стабилизированного ламинарного течения. Если относительная длина ^ℓ d трубопровода достаточно велика,

то потери напора на начальном участке трубы не учитываются.

Таким образом, при ламинарном течении независимо от числа Рейнольдса закон распределения скоростей носит квадратичный характер и для круглой трубы определяется формулой (5.6), а коэффициент Кариолиса α, учитывающий это распределение в уравнении Бернулли, равен двум (α_л = 2).

5.4. Течение жидкости в узких (капиллярных) щелях.

Данный вид течения жидкости представляет практический интерес в связи с решением задач по уплотнениям гидравлических агрегатов, герметичность соединения подвижных пар которых часто обеспечивается выполнением гарантированного малого (микронного) зазора.

Действие подобных щелевых уплотнений основано на физических свойствах реальной жидкости оказывать сопротивление сдвигающим деформациям. Математически действие такого сопротивления определяется по формуле (1.10), согласно которой касательное напряжение между двумя слоями ламинарного потока пропорционально градиенту скорости ^dυ dу по нормали к оси потока.

При практическом исследовании установлено, что течение жидкостей в капиллярных щелях до определенного размера щели подчиняется общим законам гидравлики. Критическое число Рейнольдса, при превышении которого нарушается ламинарность потока, обычно соответствует:

Rе = = 1000 …1200,

где δ – величина щели, υ – скорость течения, ν – коэффициент кинематической вязкости жидкости.

Поскольку размеры щели в гидроагрегатах обычно не превышают 10 – 15 мкм, то поток жидкости для наиболее распространенных условий работы (давлений и вязкостей жидкостей) носит обычно ламинарный характер. Исключением могут являться гидросистемы высоких температур и давлений (р > 20 МПа).

Различают плоские и кольцевые щели. Рассмотрим ламинарное течение жидкости в зазоре, образованном двумя параллельными плоскими неподвижными пластинами, расстояние между которыми равно δ (рис. 5.7).

Рис.5.7. Схема ламинарного течения жидкости в зазоре

Начало координат расположим в середине зазора, направив ось ОХ вдоль течения, ось ОУ – по нормали к пластинам. Сечениями 1-1 и 2-2 выделим объем жидкости в форме прямоугольного параллелепипеда, расположенного относительно оси ОХ и имеющего размеры сторон 2у × b × ℓ. Течение жидкости возникает под действием перепада давления ∆р = р₁ – р₂ (при р₁ > р₂). Запишем условие равновесия выделенного объема:

∆р·2у·b = τ·b·2ℓ .

∆р·2у = τ·2ℓ . (5.7)

Подставив в уравнение (5.7) выражение для касательного напряжения τ (1.11), получим:

∆р·2у = −μ ℓ . (5.8)

Знак "−" обусловлен тем, что расстояние в данном случае отсчитывают от середины потока к пластинам. Из уравнения (5.8) найдем приращение скорости dυ, соответствующее приращению координаты dу:

∆

dυ = − уdу. (5.9)

μℓ

После интегрирования уравнения (5.9) получим:

υ = ⁻^∆ у² + С (5.10)

μℓ

Постоянную С можно определить из условия движения слоев жидкости, прилегающих к пластинам (пограничные слои жидкости). При этом расстояние, отсчитываемое от середины потока, равно у = ^δ 2 , скорость пограничных слоев равна нулю (υ = 0), то постоян-

ная С будет равна:

∆

С = , μℓ

− у μℓ

откуда: υ = ^∆ ² . (5.11)

Поскольку скорость потока уменьшается соответственно второй степени величины у, то распределение скоростей по сечению потока будет параболическим.

Из рис. (5.7) видно, что максимальная скорость будет иметь место при у = 0 (для середины потока), и уравнение (5.11) в этом случае примет вид:

∆ ∆

υ_мах = = . (5.12)

μℓ μℓ

Поскольку распределение скоростей в любом сечении потока в разные стороны от оси ОХ происходит равномерно, то и средние скорости в этих "половинках"потока будут равны между собой и равны средней скорости потока по ширине δ. Известно, что средняя скорость такой "половинки"потока равна υ_ср = ² 3υ_мах . Тогда с учетом уравне-

ния (5.12) средняя скорость υ_ср будет равна:

^∆

υ_ср = υ_мах = . (5.13)

μℓ

Расход потока по ширине b равен:

∆

Q = υS = . (5.14)

μℓ

Перепад давления ∆р, под действием которого происходит движение жидкости, можно выразить из уравнения (5.14):

μℓ ℓ

∆р = Q = Q . (5.15) Приведенные расчеты проведены в предположении, что вязкость ν жидкости в щели постоянна, тогда как в действительности она зависит от давления и температуры жидкости, которые изменяют свое значение по ходу течения жидкости. При практических расчетах ввиду сложности определения кинематической вязкости вводят ее среднее значение:

νср = ,

где ν₁ и ν₂ – кинематическая вязкость жидкости при фактических температурах и давлениях на входе в зазор и на выходе из него.

Теряемая мощность эквивалентна работе, затрачиваемой на продавливание жидкости через зазор, образованный параллельными пластинами, и в соответствии с формулой (5.14) равна:

∆

N_p = ∆рQ = . μℓ

Течение через щель с подвижной стенкой. В том случае, когда одна из стенок, образующих зазор, перемещается параллельно другой, а давление в зазоре постоянно вдоль длины, подвижная стенка увлекает за собой жидкость и возникает безнапорное ламинарное движение, называемое фрикционным или течением Куэтта. Если давление изменяется по длине потока, то происходит сложение двух течений: фрикционного, обусловленного перемещением одной из плоскостей, и напорного, вызванного перепадом давлений ∆р. В зависимости от направления движения одной из плоскостей, ограничивающей поток, распределение скоростей в сечении потока будет являться результатом сложения или вычитания напорного и фрикционного течений (рис. 5.8).

Рис. 5.8. Распределение скоростей в зазоре с движущейся стенкой и перепадом давлений:

а – при совпадении фрикционного течения и напорного; б – при противополож-

ном движении напорного и фрикционного течений; 1 – эпюра напорного течения жидкости; 2 – эпюра фрикционного течения; 3 – суммарная эпюра

Расход жидкости в этом случае будет равен:

Q = ∆ ± b . (5.16) μℓ

Первое слагаемое уравнения (5.16) определяет напорное течение под действием перепада давления ∆р, второе – фрикционное течение.

Течение через кольцевую щель. Уравнением (5.16) можно воспользоваться в том случае, когда зазор образован двумя цилиндрическими поверхностями (например, поршнем и цилиндром). При этом зазор между ними мал по сравнению с диаметрами этих поверхностей, и поверхности расположены соосно (рис. 5.9, а).

Рис. 5.9. Схема концентрического (а) и эксцентрического (б) зазоров

В этом случае ширину b щели заменяют на b_д = πd, где d – средний диаметр щели, b_д – ширина щели, соответствующая длине окружности по среднему диаметру d. Если ширина b_д щели очень мала (микронный размер), то в качестве среднего диаметра d берется диаметр наружной поверхности D (b_д = 2R). Тогда с учетом этого уравнение (5.16) примет вид:

Q = ∆ ± 2πR. (5.17)

μℓ

Поскольку расход в кольцевой щели прямо пропорционален третьей степени величины зазора (Q ~ δ³), то важно обеспечить малые зазоры между внутренними и внешними цилиндрическими поверхностями.

Если поршень расположен в цилиндре с некоторым эксцентриситетом е (рис. 5.9, б), то зазор δ между ними будет величиной переменной: δ = R – r + е·cosφ = δ₀(1 + ε cosφ),

где δ₀ = R – r, ε = δ.

Выделив элемент зазора шириной r·dφ и рассматривая его как плоскую щель, можно записать с учетом уравнения (5.13) выражение для элементарного расхода: dQ = υ_ср·δ·r·dφ = ∆ δ·r·dφ = ∆ δ (1 + ε cosφ) r·dφ .

μℓ μℓ

Проинтегрировав, получим расход жидкости через эксцентричный зазор:

Q_э = ∆ δμℓ cosφ) dφ = ∆ 1 + 3 2 ε . μℓ

Q_э = Q 1 + ³ 2 ε , (5.18)

где Q – расход при соосном расположении поршня и цилиндра.

Учитывая, что максимальное значение эксцентриситета е равно номинальному радиальному зазору δ₀(ε = δ= 1), то можно записать:

Q_{э мах} = 2,5 Q .

Поскольку в соединениях, применяемых в гидроагрегатах, эксцентричность определить практически невозможно, расход жидкости через щель будет находиться в пределах расхода, определяемого для концентричной щели и щели, получаемой при максимальном эксцентриситете осей плунжера и цилиндра.

В реальных условиях размер зазора между сопрягаемыми деталями может меняться по ходу работы. Поэтому даже при небольшом увеличении зазора по направлению утечек жидкости величина утечек может повысится против расчетного значения в 2 – 2 раза.

5.5. Турбулентный режим.

Особенностью турбулентного режима движения жидкости является интенсивное перемешивание частиц жидкости, пульсации скоростей и давлений. Отдельные частицы жидкости движутся хаотично, и практически ни одна из них не повторяет траекторию другой. Линии тока также носят хаотичный характер (рис. 5.10). Любую мгновенную скорость u можно разложить на три составляющих: u_х, u_у и u_z, и для каждой построить график пульсации.

Рейнольдс предложил рассматривать мгновенные значения параметров турбулентного движения в виде суммы осредненных (во времени) значений и пульсационных составляющих (добавок). В частности, мгновенное значение местной скорости будет выглядеть: u_т = u + u' ,

где u - осредненное значение местной скорости; u'- пульсационная составляющая.

Рис. 5.10. Линии тока при турбулентном режиме

На рис. 5.11 видно, что пульсация скорости происходит около какого-то осредненного значения u. Аналогично можно усреднить все другие пульсирующие параметры турбулентного потока (в частности, нормальные р и касательные напряжения τ). Поэтому турбулентный режим можно считать условно установившимся.

Рис. 5.11. График пульсации скорости при турбулентном движении

Площадь фигуры ОАВСДЕ, заключенной между кривой u = f(t) (то есть кривой АВСД), осью абсцисс ОА, ординат ОЕ и линией ЕД, будет равна интегралу ^Тu · dt . Тогда осредненное во времени значение u_оср при условно установившемся турбулентном движении будет равно:

^Т u = Т u · dt . (5.19)

Поскольку интеграл в формуле (5.19) представляет собой площадь фигуры ОАВСДЕ, и если заменить эту площадь равновеликим прямоугольником с тем же основанием Т, то высота этого прямоугольника будет представлять собой величину осредненной скорости.

Значение осредненной скорости нельзя приравнивать к значению средней скорости, т. к. средняя скорость представляет собой не среднюю во времени скорость в данной точке, а среднюю скорость по всему живому сечению потока S:

υ_ср = · dS .

При турбулентном течении из-за перемешивания струек и обмена частицами жидкости между соседними слоями происходит выравнивание скоростей в центральной части потока; а вблизи твердой стенки находится очень тонкий слой, называемый вязким подслоем потока, в пределах которого скорость линейно увеличивается от нуля на стенке до некоторого значения u_в на границе слоя (рис. 5.12).

Рис. 5.12. Эпюра распределения скоростей при турбулентном режиме

Линейность увеличения скорости в вязком подслое потока говорит об условно ламинарном течении. Однако пульсации скорости, давления и касательного напряжения передаются и в вязкий подслой, и полностью ламинарным движение в этом слое быть не может.

Толщина вязкого подслоя δ_в оказывает влияние на структуру потока. Определение его толщины и оказываемое влияние будет рассмотрено в п.6.3.

Коэффициент Кариолиса α_тпри турбулентном режиме составляет α_т = 1,05 – 1,1. При решении практических задач для турбулентного течения жидкости принимают α_т = 1.

5.6. Примеры.

5.6.1. Определить число Рейнольдса и режим движения воды в водопроводной трубе диаметром d = 300 мм, если расход Q = 0,136 м/с. Коэффициент кинематической вязкости для воды (при t = 10 ºС ) ν = 1,306·10 м²/с.

Живое сечение потока:

S = πd 4 = 3,14 · 0,3 4 = 0,071 м2.

Средняя скорость движения воды в трубе: υ = ^Q S = ^0,136 0,071 = 1,92 м/с.

Число Рейнольдса R_е= ^υd ν = ^{1,92 · 0,3} 1,306 · 10 = 441 000.

Так как полученное R_е> R_{е кр} = 2300, следовательно, движение воды будет турбулентным.

5.6.2. По трубопроводу диаметром d = 100 мм транспортируется нефть. Определить критическую скорость, соответствующую переходу ламинарного движения жидкости в турбулентное. Коэффициент кинематической вязкости принять равным ν = 8,1·10 м²/с. Критическое число Рейнольдса равно:

dυкр. ν = 2300. Rе кр =

Откуда υкр = е.кр d = · , · , = 0,186 м/с. νR

5.6.3. Как изменяется число Рейнольдса при переходе трубопровода от меньшего диаметра к большему при сохранении постоянства расхода (Q = const)?

Скорость движения жидкости из уравнения расхода равна: υ = ^Q S = ^4Q πd .

Подставив значение скорости в уравнение Рейнольдса (5.5), получим:

R_е = ^4Q πdν .

Следовательно, число Рейнольдса уменьшится во столько раз, во сколько увеличится диаметр трубы d.

5.6.4. Контрольные вопросы.

1. В чем смысл коэффициентов гидродинамического подобия?

2. В зависимости от чего применяется тот или иной коэффициент подобия?

3. Каковы факторы, определяющие режим движения жидкости?

4. Каковы особенности ламинарного и турбулентного режимов движения жидкости?

5. Что такое осредненная скорость при турбулентном режиме движения?

6. Приведите примеры особенности ламинарного и турбулентного режимов движения жидкости.

Раздел 6 Потери напора (удельной энергии)

6.1. Общие сведения о гидравлических сопротивлениях.

Все элементы гидравлических систем оказывают различное сопротивление движению жидкости. Это приводит к энергетическим потерям, которые оценивают в виде потерь полного напора, то есть потерь полной удельной энергии жидкости. Такие потери принято называть гидравлическими потерями.

Потери удельной энергии, затрачиваемой на преодоление гидравлических сопротивлений движением вязкой жидкости, складываются из потерь двух видов:

- потерь по длине h_дл участка русла или трубы, по которым движется жидкость;

- местных потерь напора h_м (краны, задвижки, поворот трубы, сужение – расширение трубы и т. д.).

Общие потери принимают равными сумме потерь напора по длине отдельных участков и всех местных потерь напора: h_тр = ∑ h_дл + ∑ h_м .

Рассмотрим поток жидкости в прямолинейном горизонтальном трубопроводе, который встречается в повседневной жизни наиболее часто (рис. 6.1).

Рис. 6.1. Схема для определения гидравлических потерь на трение по длине

Из уравнения Бернулли, составленного для сечений 1-1 и 2-2, следует, что:

h_тр = z1 + _ρg ¹ + – z2 + _ρg² + .

Поскольку площади сечений 1 и 2 равны, то согласно уравнению расхода (3.5) скорости υ₁ и υ₂ равны между собой, и как следствие, равны коэффициенты α₁и α₂. Поскольку z₁ = z₂, то потери напора равны:

h_тр = = ^∆ . (6.1)

Установив в сечениях 1 и 2 пъезометры, можно легко определить потери напора h_тр по разности показаний уровней пъезометров.

Из выражения (6.1) следует, что гидравлические потери приводят к уменьшению давления. Они не могут приводить к изменению скоростей жидкости, которые определяются уравнением расхода (3.5).

Обычно потери напора выражают через скоростной напор. В общем случае (как для потерь по длине, так и для местных потерь напора) уравнение для определения потерь напора имеет вид:

h_тр = ζ , (6.2)

где ζ – коэффициент сопротивления (коэффициент потерь), показывающий, какому числу скоростных напоров (или долей скоростного напора) соответствует потеря напора, затрачиваемого на преодоление данного сопротивления.

Формулу (6.2) называют формулой Вейсбаха.

6.2. Местные сопротивления.

К местным сопротивлениям относят различные конструктивные элементы, которые вызывают изменение скорости движения жидкости по величине (сужение или расширение потока), направлению (поворот трубы) или по величине и направлению одновременно (например, тройник с изменением диаметра).

Несмотря на многообразие местных сопротивлений, в большинстве из них изменение скорости движения приводит к возникновению вихрей, которые для своего вращения используют энергию потока жидкости (рис. 6.2). Таким образом, основной причиной гидравлических потерь напора в большинстве местных сопротивлений является вихреобразование. Для определения этих потерь используется формула Вейсбаха (6.2)

Величина коэффициента местного сопротивления ζ_м зависит не только от вида самого местного сопротивления, но и от характера режима течения жидкости, то есть от числа Рейнольдса.

В области ламинарного режима коэффициент местного сопротивления имеет вид:

ζ_м = . (6.3)

где В – численный коэффициент, зависящий от вида местного сопротивления. Например, для выхода из трубы в бак В = 30, а для угольника при α = 90º В = 400.

Рис. 6.2. Схема для определения гидравлических потерь в местном сопротивлении

В гидросистемах с ламинарными потоками в большинстве случаев местные потери напора малы по сравнению с потерями на трение по длине, поэтому чаще всего их приравнивают к эквивалентным потерям по длине потока.

При турбулентном режиме течения жидкости изменения коэффициента ζ_м в зависимости от числа Рейнольдса настолько незначительны, что ими можно пренебречь. Поэтому при практических расчетах в области турбулентного режима этот коэффициент считают зависящим только от характера и конструкции местного сопротивления.

Большинство коэффициентов местных сопротивлений найдены экспериментально и составляют табличные данные. Например, коэффициент ζ_м для поворота трубы зависит от радиуса поворота, для крана – от угла его открытия и т. д. Исключение, пожалуй, составляет только сопротивление в виде внезапного сужения или расширения потока, для которых коэффициент ζ_м определяется по формулам.

Для внезапного расширения потока:

ζ_р = 1 − _S , (6.4) где S₁ и S₂ – площади сечения потока до и после внезапного расширения.

Для внезапного сужения потока:

S ζ_с = 0,5 1 − _S , (6.5) где S₁ и S₂ – площади сечений потока до и после сужения.

Значения коэффициентов для постепенного расширения ζ_п.р.и постепенного сужения ζ_п.с.находят с введением поправочных коэффициентов в формулы (6.4) и (6.5): ζ_п.р.=κ_рζ_р и ζ_п.с.=κ_сζ_с. Поправочные коэффициенты κ_р и κ_с зависят от плавности перехода и имеют численное значение меньше единицы. Их значения приводятся в справочниках.

6.3. Потери напора по длине потока.

Потери напора по длине – это потери энергии, которые возникают в прямых трубах постоянного сечения, то есть при равномерном течении, и возрастают пропорционально длине трубы.

Потери на трение по длине обусловлены:

- геометрическими параметрами трубопровода. К ним относятся: длина по направлению движения ℓ, диаметр сечения потока d, размеры выступов шероховатости стенок (∆ - высота выступа, ℓ_∆ - характерный продольный размер выступа шероховатости);

- физическими свойствами жидкости (ρ – плотность, μ – динамическая вязкость и Е₀ – модуль упругости);

- режимом течения жидкости, то есть числом Рейнольдса.

В общем случае формула Вейсбаха (6.2) для определения потерь по длине имеет вид:

ℓ

h_тр = λ , (6.6)

где λ – коэффициент потерь на трение по длине или коэффициент Дарси.

Формулу (6.6) обычно называют формулой Дарси – Вейсбаха.

Для напорного движения в круглых трубах коэффициент Дарси имеет следующую зависимость:

λ = f(^∆ d ;^ℓ^∆ d ; R_е ).

Рассмотрим зависимость коэффициента Дарси от режимов течения жидкости, то есть от числа Рейнольдса. Коэффициент Дарси при ламинарном напорном движении в трубе определяется по формуле:

λ_л = . (6.7)

Подставив в формулу (6.7) выражение для числа Рейнольдса R_е (5.5), получим:

λ_л = . (6.8)

Ламинарный режим течения. При рассмотрении ламинарного течения жидкости необходимо выявить зависимость потерь напора на трение от расхода жидкости, что важно для исследования работы гидравлических систем с ламинарными потоками.

Для этого подставим в формулу Дарси – Вейсбаха (6.6) зависимость (6.8), и с учетом формулы (5.5) получим:

ℓ ℓ ℓ h_тр = е = = .

В последнее математическое выражение подставим значение средней скорости, выраженное из уравнения расхода(3.5):

υ = = .

Тогда получим следующее выражение для определения потерь напора при ламинарном режиме течения жидкости: ℓ

h_тр = Q . (6.9)

Зависимость (6.9) носит название формулы Пуазейля и широко применяется при расчетах машиностроительных гидросистем.

Формула Пуазейля показывает, что гидравлические потери при ламинарном течении пропорциональны расходу. График этой зависимости представляет собой прямую линию (рис. 6.3), поэтому такие потери называют линейными.

Рис. 6.3. Зависимость потерь от расхода при ламинарном течении

Следует учесть, что наклон линии на рис. 6.3 зависит от геометрических параметров трубопровода ℓ и d, а также от свойств рабочей жидкости. Кинематическая вязкость ν, значение которой входит в формулу (6.9) для определения потерь, существенно зависит от температуры. Таким образом, на зависимость гидравлических потерь напора от расхода при ламинарном течении влияет изменение температуры жидкости.

Турбулентный режим течения. Для оценки гидравлических потерь напора при турбулентном режиме также используется формула Дарси – Вейсбаха (6.6). Однако значение коэффициента потерь λ зависит не только от числа Рейнольдса (как в ламинарных потоках), но и от шероховатости стенок трубы.

В качестве характеристики шероховатости выбирают некоторую среднюю высоту выступов шероховатости ∆. Соотношение между высотой выступов ∆ и толщиной вязкого подслоя δ_в определяет структуру потока.

Если высота выступов шероховатости ∆ меньше, чем толщина вязкого подслоя δ_в, то все неровности погружены в этот подслой и не оказывают влияния на особенности движения и потери напора. Такие стенки и трубы называют гидравлически гладкими (рис. 6.4, а).

Рис. 6.4. Схема гидравлически гладких (а) и гидравлически шероховатых (б) труб

Если высота выступов шероховатости ∆ превышает толщину вязкого подслоя δ_в, то в этом случае поток обтекает выступы с отрывом, что приводит к интенсивному перемешиванию частиц (вихреобразованию). В этом случае потери напора зависят от шероховатости, и такие трубы называют гидравлически шероховатыми (рис. 6.4, б).

Поэтому при определении потерь напора по длине потока при турбулентном режиме необходимо определить толщину вязкого подслоя:

δ_в = . (6.10)

Таким образом, с увеличением числа R_е и коэффициента Дарси λ толщина вязкого подслоя уменьшается.

Коэффициент Дарси λ в гидравлически гладких трубах определяется по формуле Блазиуса:

λ_гл = _,_е . (6.11)

Для труб промышленного изготовления с естественной шероховатостью для любой области сопротивления при турбулентном режиме движения применяется универсальная формула Альтшуля:

λ_т = 0,11^∆⁺^,. (6.12)

∆

При << формула (6.12) практически совпадает с форму е

лой Блазиуса (6.11).

Зависимость потерь напора от расхода при турбулентном режиме изображена на рис. 6.5.

Рис. 6.5. Зависимость потерь напора от расхода при турбулентном движении

Как было отмечено выше, при ламинарном режиме гидравлические потери пропорциональны расходу. Это отражено отрезком ОА (будем считать движение жидкости в вязком подслое условно ламинарным). Затем происходит некоторый скачок сопротивления (отрезок АВ), что соответствует области перехода от ламинарного режима движения к турбулентному. Далее при турбулентном течении происходит более крутое нарастание потерь h_тр, степень зависимости которых от расхода является квадратичной параболой или близка к ней

(h_тр ~ Q²).

Схема по определению потерь напора в круглых трубах представлена в приложении 2.

Коэффициент сопротивления системы. Если трубопровод длиной ℓ имеет несколько n – участков с различными диаметрами и на каждом участке имеются мастные сопротивления, то:

hтр.сист. = ∑ hдл + ∑ hм .

Поскольку скорости на различных участках не равны, то их выражают через одну (например, на последнем n–ом участке) υ_n. Тогда:

hтр.сист. = ζсист .

Коэффициент сопротивления системы будет равен:

ζсист. = ∑ζдл + ∑ζм .

6.4. Примеры.

6.4.1. Вентиляционная труба d = 0,1 м имеет длину ℓ = 100 м. Определить потери давления, если расход воздуха, подаваемый по трубе, равен Q = 0,078 м³/с. Давление на выходе равно атмосферному (p_ат = 0,1 МПа). Местные сопротивления по пути движения воздуха отсутствуют. Кинематическая вязкость воздуха при t = 20 ºС составляет ν = 15,7·10^-⁶ м²/с. Средняя шероховатость выступов ∆ = 0,2 мм, плотность воздуха ρ = 1,18 кг/м³.

Скорость воздуха в трубе равна:

· ,

υ = = = _{,
· ,} = 10 м/с.

Число Рейнольдса:

· ,

R_е= = , · = 69 000.

Режим течения жидкости – турбулентный (R_е >2300), поэтому коэффициент гидравлического трения определим по формуле Альтшуля (6.12):

∆ , ,

λ_т = 0,11 + = 0,11 + = 0,0257. е

Потери давления на трение по длине определим по формуле Дарси–Вейсбаха (6.6):

∆ ℓ

h_тр = = λ , откуда

ℓ

∆р = λ ρ = 0,0257 · + ·1,18 =1,5 кПа.

6.4.2. При внезапном расширении трубы от d = 50 мм до D = 150 мм происходит увеличение давления, которому соответствует разность показаний пъезометров ∆h = 80 мм. Определить скорости υ₁и υ₂ и расход жидкости. Учесть потери на внезапное расширение.

Составим уравнение Бернулли для сечений 1 и 2 (z₁ = z₂ = 0):

+ = + + hм.

Потери на внезапное расширение определим по формулам (6.2) и (6.4):

. hм = 1 −

Учтем также, что ∆h = – . Выразим любую скорость (на-

пример, υ₂) из уравнения расхода:

υ₂ = υ₁ .

С учетом вышеизложенного уравнение Бернулли примет вид:

∆h = – – h_м= – – 1 − Dd22 2g .

Откуда скорость υ₁ будет равна:

∆ · , · · ,

υ1 = = – = 2,83 м/с.

–

υ₂ = υ₁· =2,83· = 0,31 м/с.

Расход жидкости определим из уравнения расхода:

, · ,

Q = υ₁S₁ = υ₂S₂= 2,83· = 5,55 л/с.

6.4.3 Вода перетекает из напорного бака, где избыточное давление воздуха р₁ = 0,3 МПа, в открытый резервуар по короткой трубе диаметром d =50 мм, на которой установлен кран. Чему должен быть равен коэффициент сопротивления крана для того, чтобы расход воды составлял Q = 8,7 л/с. Высоты уровней Н₁ = 1м, Н₂ = 3 м. Учесть потери напора на входе в трубу (ζ_вх = 0,5) и на выходе из трубы (внезапное расширение).

Скорость в трубе из уравнения расхода:

· ,

υ = = = _{,
· ,} = 4,4 м ⁄с.

Составим уравнение Бернулли для сечений 1 и 2 относительно плоскости сравнения, совпадающей с осью трубы:

Н1 + ат + = Н2 + ат + + ∑hтр .

Скоростями υ₁ и υ₂ можно пренебречь, то есть υ₁= υ₂ = 0. Потери напора равны:

∑hтр = hсуж + hм + hрасш.

Потери напора при сужении:

hсуж = ζвх ,

где υ - скорость течения жидкости в трубе.

Потери напора при расширении по формуле (6.4):

hрасш = 1 − .

Поскольку S₂ >> S₁, то:

h_расш = . Местные потери напора:

h_м = ζ_к .

Тогда уравнение Бернулли примет вид:

Н₁ + = Н₂ + ζ_вх + ζ_к + .

Перегруппировав члены уравнения и выразив ζ_к, получим:

[^Н Н ρ ^υ (^ζ_вх )]· (Н Н )

ζ_к = = – (ζ_вх + 1) =

· , ·( ) ·

= , –1,5 = 27,5.

6.4.4. Контрольные вопросы.

1. Из чего складываются потери напора?

2. От чего зависит коэффициент местного сопротивления?

3. Чем объясняются потери по длине трубопровода?

4. Как влияет режим течения жидкости на потери напора по длине и в местных сопротивлениях?

5. Почему на зависимость гидравлических потерь напора от расхода при ламинарном течении влияет изменение температуры жидкости?

6. Почему существуют понятия "гидравлически гладкие трубы" и "гидравлически шероховатые трубы"?

7. Почему толщина вязкого подслоя жидкости влияет на потери напора при турбулентном движении?

8. В чем разница между линейными потерями и квадратичными?

Раздел 7 Истечение жидкости

7.1. Истечение через отверстие в тонкой стенке при постоянном напоре.

Задача об истечении жидкости из отверстий является одной из основных задач гидравлики, отправной точкой ее развития. Основное уравнение гидродинамики (уравнение Бернулли) – было получено в результате одного из подобных решений.

Задача об истечении сводится к определению скорости истечения и расхода вытекающей жидкости.

Истечение может происходить в газообразную среду (свободное истечение) или в жидкость (затопленное истечение) при постоянном или переменном напоре. Истечение жидкости через затопленное отверстие называют также истечением под уровень. Наиболее простым случаем истечения жидкости является истечение при постоянном напоре.

При постоянном напоре скорости истечения будут неизменны во времени, то есть движение будет установившееся. При этом линии тока и траектории частиц будут совпадать (рис. 7.1).

Скорости истечения на верхней и нижней границах вытекающей из отверстия струи можно считать одинаковыми, если истечение происходит из малого отверстия. Малое отверстие – это отверстие, у которого наибольший вертикальный размер d не превышает 0,1Н.

Рис. 7.1. Схема истечение жидкости через отверстие при постоянном напоре в газовую среду

Рассмотрим истечение жидкости через отверстие диаметром d в стенке бака, расположенное на глубине Н, в газовую среду с давлением р_с через незатопленное отверстие с острой кромкой. Свободная поверхность жидкости в резервуаре находится под давлением р₀.

Частицы жидкости, приближаясь к отверстию, двигаются из всего близлежащего объема по различным траекториям. Многие из них при попадании в отверстие должны изменить направление своего движения на 90º. Поскольку каждая частица жидкости имеет свою массу, то мгновенно изменить направление своего движения она не может. Следствием этого является сжатие струи жидкости при истечении (рис. 7.2).

Рис. 7.2. Схема деформирования струи при истечении

Формирование сжатого сечения струи заканчивается на расстоянии, примерно равном 0,5d. Необходимо отметить, что сжатие струи происходит при истечении жидкости через отверстие с острой кромкой или через отверстие в тонкой стенке. Стенка считается тонкой, если толщина стенки не превышает диаметра отверстия. В этом случае отверстие, через которое происходит истечение, не влияет на сам характер истечения.

Отношение площади струи в сжатом сечении d_с к площади отверстия d называется коэффициентом сжатия струи:

ε = ₌ , (7.1)

где S и S_c - площади отверстий в тонкой стенке и в сжатом сечении струи соответственно.

Чтобы получить формулы для определения скорости и расхода жидкости, применим уравнение Бернулли для сечений А-А и С-С, движение жидкости в которых можно считать равномерным. Горизонтальную плоскость (плоскость сравнения) удобно провести через центр сжатого сечения. Тогда уравнение Бернулли примет вид:

Н + + = ^с + ^с^с + h_тр , (7.2) где Н – глубина погружения центра тяжести выходного отверстия в стенке резервуара; р₀ и р_с – давление выбранных точках в сечениях А-А и С-С; υ₀ и υ_с – средняя скорость движения жидкости соответственно в сечениях А-А и С-С; h_тр – потери напора (удельной энергии) на участке между выбранными сечениями; α₀ и α_с – коэффициент Кариолиса, учитывающий неравномерность распределения скоростей по сечению.

Скорость υ₀ течения жидкости в сечении в сечении А-А очень мала, и ею можно пренебречь. Давление Р_с в сечении С-С равно атмосферному (Р_с = Р_ат). Потери удельной энергии (в данном случае местные потери) будут равны:

_с

h_тр = ζ_о.к. , (7.3)

где ζ_о.к. – коэффициент потерь при истечении через отверстие с острой кромкой или тонкой стенкой.

Тогда с учетом выше изложенного и формулы (7.3) уравнение (7.2) примет вид:

с с _с _с

Н + + = + + ζ_о.к. .

Перенесем первое слагаемое в правой части уравнения в левую часть и назовем эту сумму действующим или расчетным напором Н_р:

Нр = Н + с = (αс + ζо.к.) с .

Для средней скорости в сжатом сечении получим:

υ_с = αс ζо.к. 2gН_р = φ 2gН_р , (7.4)

где φ – коэффициент скорости (безразмерная величина), определяемая по формуле:

φ = . (7.5) αс ζо.к.

Коэффициент скорости φ отражает влияние распределения скоростей в сжатом сечении α_с и потерь напора ζ_о.к. .

В случае истечения идеальной жидкости (α_с = 1; ζ_о.к = 0) из формулы (7.5) следует, что φ = 1, то есть скорость истечения идеальной жидкости равна:

υ_и = 2gН_р . (7.6)

На основании формул (7.4) и (7.6) можно сделать заключение, отражающее физический смысл коэффициента скорости: φ – это величина, равная отношению средней скорости истечения реальной жидкости к скорости истечения идеальной жидкости при тех же условиях:

φ = υ^с υ_и .

При истечении реальной жидкости коэффициент φ < 1. Расход жидкости с учетом формулы (7.1) будет равен:

Q = S_c υ_c = ε S υ_c. Используя формулу (7.4),получим:

Q = εφS 2gН_р .

Обозначив μ = εφ, найдем расход при истечении жидкости через отверстие:

Q = μS 2gН_р . (7.7)

Произведение двух безразмерных коэффициентов ε и φ называют коэффициентом расхода μ = ε φ.

Из формулы (7.7) следует, что:

μ = = = , Нр и и

где Q_и – идеальный расход, который имел бы место при отсутствии сжатия струи и сопротивления истечению.

Таким образом, физический смысл коэффициента расхода μ состоит в тои, что он численно равен отношению действительного расхода к идеальному.

Необходимо отметить, что Q_и не является расходом при истечении идеальной жидкости, так как эффект сжатия струи при истечении идеальной жидкости при отсутствии вязкости проявился бы еще в большей степени.

Для практического использования формулы (7.7) сделаем следующие преобразования. Обозначим внутри бака (рис.7.1) на уровне оси отверстия диаметром d на некотором отдалении от него (где скорость жидкости можно принять равной нулю) давление р₁.

Тогда перепад давления ∆р, под действием которого происходит истечение жидкости через отверстие, будет равен:

∆р = р₁ – р_с = (р₀ + ρgН) – р_с = ρgН_р. (7.8)

Выразив из формулы (7.8) расчетный напор Н_р и подставив его в формулу (7.7), получим:

Q = μS∆ . (7.9)

При помощи формулы (7.9) решается основная задача по определению расхода жидкости при истечении.

Коэффициенты ε, φ и μ, характеризующие процесс истечения жидкости, являются функцией числа Рейнольдса R_е. Зависимость этих коэффициентов от числа R_еи(число Рейнольдса, подсчитанное для идеальной скорости истечения), изображена на рис. 7.3.

Рис. 7.3. Зависимость ε, φ и μ от R_еи для круглого отверстия в тонкой стенке

Как видно из рисунка, коэффициент φ с увеличением R_еи до 10⁵ растет, так как влияние сил вязкости при увеличении R_е уменьшается (это видно из формулы 5.5), и следовательно, коэффициент сопротивления ζ уменьшается. При значительных R_е коэффициент φ можно считать постоянным и равным φ = 0,97.

Коэффициент сжатия ε с увеличением R_еи уменьшается, а при R_еи > 10⁵его можно считать постоянным и равным ε = 0,64.

Зависимость μ от R_еи более сложная. Коэффициент расхода μ, определяемый произведением ε и φ, с увеличением R_еи сначала увеличивается, что обусловлено крутым возрастанием φ, а затем, достигнув максимального значения, уменьшается в связи со значительным падением ε и при больших R_е практически стабилизируется на значении, равном μ = 0,62.

7.2. Истечение под уровень.

При истечении через отверстие под уровень жидкости отверстие называют затопленным.

Рассмотрим истечение через затопленное отверстие при условии, что положение свободных поверхностей жидкости по обе стороны от отверстия не изменяются во времени (рис. 7.4).

Рис.7.4. Схема истечения жидкости через отверстие в тонкой стенке под уровень

Составим уравнение Бернулли для сечений А-А и В-В, совпадающих со свободной поверхностью жидкости до отверстия и за ним. Плоскость сравнения проведем через центр отверстия. Пренебрегая скоростными напорами в выбранных сечениях, получим:

z₁ + = z₂ + + h_тр . (7.10)

Потери напора между сечениями А-А и В-В (h_тр) складываются из двух составляющих:

- потери напора между сечениями А и С, аналогичные потерям при истечении в атмосферу через малое отверстие с острой кромкой:

ho = ζо.к. ;

- потери напора между сечениями С и В, связанные с внезапным расширением струи от сжатого сечения до сечения во втором резервуаре

_с .

h_вр = α_с

Обозначим Н = z₁ – z₂. Тогда с учетом того, что h_тр = h_о + h_вр, и перегруппировав члены уравнения (7.10), получим:

Н + = (ζо.к. + αс) с .

Если в этом уравнении принять Н + = Н_р, то после пре

образований получим формулу, определяющую значение средней скорости жидкости в сжатом сечении струи:

υ_с = αс ζо.к. 2gН_р = φ 2gН_р .

Получили ту же формулу, что и при истечении жидкости в атмосферу. Это значит, что формула, определяющая расход Q при истечении под уровень, будет аналогична формулам при истечении жидкости в атмосферу (7.7) и (7.9).

Коэффициенты ε, φ и μ, использующиеся в этих формулах, в обоих случаях истечения имеют одинаковые значения при равенстве соответствующих чисел Рейнольдса.

Необходимо отметить, что при определении расхода Q при истечении жидкости через проходные сечения в гидравлических устройствах, кроме оценки коэффициента расхода μ, необходимо определять площадь проходного сечения S отверстия в соответствии со смещением одной из деталей относительно другой.

7.3. Примеры.

7.3.1. Определить расход и скорость вытекания воды из малого круглого отверстия диаметром d = 3 см в боковой стенке резервуара больших размеров. Напор над центром отверстия Н = 1 м, кинематическая вязкость воды при t = 20 ºС составляет ν = 10^-⁶ м²/с.

Определяем число Рейнольдса, характеризующее истечение без учета коэффициента скорости φ:

R_е= = = =133 000.

Из рис. 7.2 при R_е = 133 000 определяем коэффициенты скорости φ и расхода μ: φ = 0,98; μ = 0,59. Тогда скорость истечения воды из отверстия будет равна:

υ_с = φ 2gН =0,98 =4,3 м/с.

Расход вытекающей из отверстия воды будет равен:

, · ,

Q = μS 2gН = 0,59· = 1,91 л/с.

7.3.2. Определить расход жидкости (ρ = 800 кг/м³), вытекающей из бака через отверстие площадью S = 1 см². Показание ртутного манометра h = 268 мм, высота Н = 2 м, коэффициент расхода μ отверстия μ = 0,60.

Расход жидкости определяем по формуле (7.9): Q = μS∆ .

Перепад давления ∆р с верхней и нижней стороны отверстия будет равен разности давления на дне сосуда (сумма р₀ и весового давления ρgН) и атмосферного давления, то есть ∆р = р₀ + ρgН - р_ат. Давление р₀ (абсолютное давление) определяется как р₀ = р_ат+ ρ_рт gh = 100 000 + 13 600·9,8·0,268 = 135,72 кПа.

∆р = р₀ +ρgН – р_ат = 135 720 + 800·9,8·2 – 100 000 = 51,4 кПа.

Q = 0,6·0,000151 400 = 0,68 л/с.

7.3.3. Определить направление истечения жидкости с плотностью ρ = 1000 кг/м³ через отверстие d₀ = 5 мм и расход, если разность уровней Н = 2 м, показание вакуумметра соответствует 147 мм. рт. ст., показание манометра h_м=0,25 МПа, коэффициент расхода μ = 0,62.

Разность давлений между баками равна:

∆р = р_м – (ρgН – р_вак.) = 250 000 – (1000·9,8·2 – 147·133,3) = 250 кПа.

Поскольку давление в правой части больше, то направление течения жидкости будет направлено в левую часть двойной емкости.

Тогда расход жидкости через отверстие с диаметром d₀ будет равен:

, · ,

Q = μS∆ = 0,62 · 250 000 = 0,27 л/с.

7.3.4. Определить диаметр отверстия дросселя, установленного на сливе из гидроцилиндра, при условии движения штока цилиндра под действием внешней нагрузки F= 60 кН со скоростью υ = 200 мм/с. Диаметры: штока d_ш = 40 мм, цилиндра D = 80 мм, коэффициент расхода дросселя μ = 0,65, плотность жидкости ρ = 850 кг/м³, давление на сливе р_с = 0,3 МПа.

Определим давление, которое создает сила F в правой части гидроцилиндра:

р = ( ш) = , ( , , ) = 16 МПа.

Перепад давлений на дросселе ∆р будет равен:

∆р = р – р_с = 15,7 МПа.

Расход жидкости, протекающей через дроссель:

( ) , ( , , )

Q = υS =υ = 0,2 · = 0,75 л/с.

Площадь сечения дросселя S будет равна:

, ^-⁵ м². S = = = 0,6·10 μ ∆ , Тогда диаметр отверстия дросселя:

d = 4S π = ^{4 ·
0,6 · 10} 3,14 = 2,76 мм.

7.3.5. Контрольные вопросы.

1. При выполнении какого условия отверстие называют малым?

2. В чем физический смысл коэффициента скорости?

3. Какова зависимость коэффициентов сжатия, скорости и расхода от числа Рейнольдса?

4. Чем отличается формула расхода жидкости для незатопленного и затопленного отверстия?

Раздел 8 Гидравлический расчет трубопроводов

8.1. Классификация трубопроводов.

При гидравлических расчетах рассматривается несколько видов трубопроводов.

Простые трубопроводы не имеют ответвлений и состоят из труб одинакового диаметра, выполненных из одного материала. Они могут соединяться между собой как последовательно (простой трубопровод переменного сечения), так и параллельно.

Трубопровод, содержащий как последовательные, так и параллельные соединения труб, называется сложным.

Жидкость движется по трубопроводу благодаря тому, что ее энергия в начале трубопровода больше, чем в конце. Эта разность энергий достигается тем или иным способом: работой насоса, давлением газа или благодаря разности уровней жидкости.

В общем случае при расчете трубопровода определению подлежат диаметр трубопровода и напор в его начальном сечении.

8.2. Расчет простых трубопроводов.

По определяемым параметрам и методике расчета простых трубопроводов задачи делят на три группы:

- при известном диаметре d, длине ℓ и заданном расходе Q требуется определить напор;

- определить расход Q, зная действующий напор Н и параметры трубопровода;

- определить диаметр трубопровода, если известен действующий напор Н, расход Q и длина водопровода ℓ.

Во всех трех случаях известны плотность жидкости, кинематическая вязкость и шероховатость стенок трубопровода.

Каждую задачу решают с помощью уравнения Бернулли (4.17) и уравнения неразрывности (3.5).

Рассмотрим расчет простого трубопровода при установившемся истечении жидкости в атмосферу (рис. 8.1) и под уровень

(рис. 8.2).

Истечение жидкости в атмосферу.Составим уравнение Бернулли для сечений 1-1 и 2-2:

z1 + + = z2 + + + hтр . (8.1)

Напор, который нужно создать для течения жидкости самотеком, будет равен разности геометрических высот z₁и z₂. Будем называть его действующим напором Н_дейст. :

Н_дейст. = z₁ – z₂ = ∆z.

Скорость υ₁ в сечении 1-1 очень мала, поэтому примем ее равной

нулю ( = 0). Тогда:

Н_дейст.= + hтр . (8.2)

Рис. 8.1. Схема истечения жидкости в атмосферу

Сумма потерь напора h_тр по длине трубопровода при ламинарном режиме движения жидкости будет определяться по формуле

Пуазейля (6.9):

ℓ

h_тр = Q . (6.9)

Формула (6.9) отражает только потери по длине. Дело в том, что местные потери напора при ламинарном режиме невелики, и их заменяют эквивалентными длинами сопротивлений по длине потока.

При турбулентном режиме движения потери напора будут равны сумме потерь напора по длине потока и потерь напора в местных сопротивлениях:

h_тр. = ∑ h_дл + ∑ h_м = λ_т + ζ_м = (λ_т ℓ + ζ_м) . (8.3)

Подставим в уравнение (8.3) скорость, выраженную из уравнения расхода (3.5):

ℓ

h_тр. = (λ_т + ζ_м) . (8.4)

Данная задача сводится к определению расхода жидкости Q, поскольку остальные члены уравнений (6.9) или (8.4) известны и имеют численное значение. Обозначим их буквой К. Тогда при любом режиме движения при истечении жидкости самотеком в атмосферу действующий напор Н_дейст.будет равен сумме скоростного напора и суммарных потерь напора:

Н_дейст.= ^m , (8.5)

+ КQ

где К и m – величины, зависящие от режима течения жидкости в трубопроводе и характеристик местных сопротивлений.

Как видно из формул (6.9) и (8.4), степень m при ламинарном течении равна единице (m = 1), а при турбулентном – двум (m = 2). Поэтому говорят, что при ламинарном течении жидкости потери напора носят линейный характер, а при турбулентном – квадратичный.

Итак, действующий напор при истечении в атмосферу расходуется на создание кинетической энергии потока на выходе (которую можно использовать, например, в турбинах), и на преодоление потерь напора.

Истечение под уровень. Составим уравнение Бернулли для сечений 1-1 и 2-2 (рис. 8.2). После всех сокращений и преобразований получим, что действующий напор равен сумме потерь напора:

Н_дейст.= h_тр . (8.6)

Тогда с учетом формул (6.9) и (8.4) выражение (8.6) примет вид:

Рис. 8.2. Схема истечения жидкости под уровень

Н_дейст.= КQ^m. (8.7)

В данном случае действующий напор целиком расходуется на преодоление гидравлических сопротивлений.

Течение с избыточным давлением в начальном сечении. Пусть простой трубопровод постоянного сечения длиной ℓ и диаметром d расположен произвольно в пространстве и содержит ряд местных сопротивлений (рис. 8.3).

Рис. 8.3. Схема простого трубопровода.

Составим уравнение Бернулли для сечений 1-1 и 2-2:

z1 + + = z2 + + + hтр. .

Для течения жидкости в сечении 1-1 необходимо создать дос-

таточное для этого давление р₁. Соответствующий напор ρg назо-

вем потребным напором Н_потр.:

Нпотр. = ρg .

Сумма разности геометрических высот z₁и z₂ и пъезометриче-

ской высоты ρg называется статическим напором Н_ст:

Н_ст = ∆z + ρg .

Потери напора можно представить как степенную функцию расхода Q:

h_тр = КQ^m.

Тогда с учетом вышеизложенного уравнение Бернулли примет вид:

Н_потр. = Н_ст + КQ^m. (8.8)

Графическая характеристика потребного напора. Формула (8.8) является основой для расчета простых трубопроводов. По ней можно построить кривую потребного напора в зависимости от расхода жидкости в трубопроводе. Такая зависимость называется характеристикой потребного напора. Рассмотрим методику построения такой зависимости (рис. 8.4).

Рис. 8.4. Кривая потребного напора

Этап первый. Используя формулу Rе = ^4Q πdν , полученную

из формул (5.5) и (3.5), определяем значение критического расхода Q_кр, соответствующее R_кр = 2300. Очевидно, что для всех расходов, расположенных левее Q_кр, в трубопроводе будет ламинарный режим движения; а для расходов, расположенных правее Q_кр - турбулентный.

Этап второй. Рассчитываем значения потребного напора Н₁ и Н₂ при расходе в трубопроводе, равном Q_кр по формуле (8.8) предполагая, что Н₁ – результат расчета при ламинарном режиме течения жидкости, а Н₂ – при турбулентном.

Этап третий. Строим характеристику потребного напора для ламинарного режима течения, причем эта характеристика имеет линейную зависимость.

Рис. 8.5. Характеристика потребного напора при ламинарном (а) и турбулентном

(б) режимах

Этап четвертый. Строим характеристику потребного напора для турбулентного режима течения, и эта характеристика представляет собой криволинейную линию, близкую к параболе второй степени.

На рис. 8.5 изображена зависимость потребного напора от расхода жидкости в трубопроводе при ламинарном и турбулентном режимах течения.

Величина Н_ст положительна в том случае, когда жидкость поднимается или движется в полость с повышенным давлением; и отрицательна при опускании жидкости или движении в полость с разряжением. Точка пересечения кривой потребного напора с осью абсцисс при Н_ст = 0 (точка А) определяет расход при движении жидкости самотеком, то есть за счет лишь разности геометрических высот ∆z. Потребный напор в этом случае равен нулю, т. к. давление в начале и в конце трубопровода равно атмосферному. Такой трубопровод называется самотечным.

8.3. Соединения простых трубопроводов.

Последовательное соединение. Пусть имеется несколько простых трубопроводов различной длины разного диаметра, с различным набором местных сопротивлений (рис. 8.6, а).

Рис. 8.6. Схема последовательного соединения трубопровода (а) и соответствующая ей характеристика (б)

Очевидно, что по всему сечению такого трубопровода расход жидкости Q будет одинаков, а потеря напора для всего соединения будет равна сумме потерь напора в каждом простом трубопроводе:

_h_трQ = Q^Q_h. (8.9)

Потери напора могут быть определены через значения соответствующих расходов:

К Q

КQ (8.10)

К Q

Совместное решение уравнений (8.9) и (8.10) является основой для расчета гидросистемы с последовательным соединением трубопроводов.

При графическом методе расчета строят суммарную характеристику соединения. Для этого строятся характеристики простых трубопроводов по зависимостям (8.10), затем складываются по зависимости (8.9) (рис. 8.6, б).

Поскольку скорости в точках А и В различны, то выражение (8.8) примет несколько иной вид: РА = Н = z – z + В А + РА . потр B A

Выражение (^В^А) выразим через расход Q:

В А = − А , В

где S_А и S_В – площади соответствующих сечений. Обозначим С = ⁻_А, тогда выражение для потреб-

_В

ного напора примет вид:

Нпотр. = Нст +СQ2 + КQm .

Параллельное соединение. Рассмотрим параллельное соединение нескольких простых трубопроводов (рис.8.7, а).

Рис. 8.7. Схема параллельного соединения трубопроводов (а) и соответствующая ему характеристика (б)

Очевидно, что расход жидкости Q до точки А и после точки В один и тот же и равен сумме расходов в параллельных ветвях:

Q = Q₁ + Q₂ + Q₃ . (8.11)

Потери напора в каждом из трубопроводов равны между собой:

h . (8.12)

Это следует из того, что = Н_А – Н_В; = Н_А – Н_В;

= Н_А – Н_В; и объясняется распределением расходов Q₁, Q₂ и Q₃ таким образом, что потери в параллельных ветвях трубопровода остаются равными.

Таким образом, совместное решение уравнений (8.11) и (8.12) позволяет рассчитать параллельное соединение простых трубопроводов.

Для получения суммарной характеристики параллельного соединения необходимо сложить расходы в исходных трубопроводах при одинаковых потерях напора (рис. 8.7, б).

Разветвленное соединение. Это совокупность нескольких простых трубопроводов, имеющих одно общее место разветвления

(рис. 8.8, а).

Рис. 8.8. Схема разветвленного соединения трубопроводов (а) и соответствующая ей характеристика (б).

Так же, как и для параллельных трубопроводов, расход Q до точки А равен сумме расходов в ветвях трубопровода:

Q = Q₁ + Q₂ + Q₃ .

Потребный напор в соответствии с (8.8) будет равен:

Н_А = Н_ст₁ + К₁Q₁^m = Н_ст₂ + К₂Q₂^m = Н_ст₃ + К₃Q₃^m. (8.13)

Таким образом, получаем систему уравнений из четырех неизвестных: Q₁, Q₂, Q₃ и Н_потр.

Построение кривой потребного напора для разветвленного трубопровода выполняется сложением кривых потребных напоров по правилу сложения характеристик параллельных трубопроводов (рис.

8.8, б).

Сложные трубопроводы. Сложный трубопровод в общем случае составлен из простых трубопроводов с последовательным и параллельным их соединением или с разветвлениями.

Рассмотрим сложный трубопровод, составленный из последовательных и параллельных соединений (рис. 8.9, а).

Рис. 8.9. Схема сложного трубопровода (а) и соответствующая ей характеристика (б).

Расчет сложных трубопроводов ведут по формулам (8.8) – (8.13), либо графическим методом, что предпочтительнее.

При графическом методе (рис. 8.9, б), сложный трубопровод разбивается на ряд простых. Потом для каждого простого трубопровода строится его характеристика. Затем производят сложение характеристик как для параллельного трубопровода ( = ), затем как для последовательного ().

Имея построенный таким образом график для сложного трубопровода, достаточно легко по известному значению расхода Q₁, поступающему в гидросистему, определить потребный напор Н_потр.для всего сложного трубопровода, расходы Q₂ и Q₃, а также потери напора в каждом простом трубопроводе.

8.4. Трубопровод с насосной подачей.

Трубопровод, в котором движение жидкости обеспечивается за счет насоса, называется трубопроводом с насосной подачей.

Насосом называется гидравлическое устройство, которое преобразует механическую энергию привода в энергию потока рабочей жидкости.

Целью расчета трубопровода с насосной подачей является определение напора, создаваемого насосом. Напором насоса называется полная удельная механическая энергия, передаваемая насосом жидкости, то есть это разность полных напоров на входе и выходе насоса:

Н = Н_вых.– Н_вх.. (8.14)

Рассмотрим работу разомкнутого трубопровода с насосной подачей (рис. 8.10).

Составим уравнение Бернулли для сечений 0-0 и 1-1:

Р Р

0 + + = Н₁ + ⁺_2g + h_тр₁ .

Рис. 8.10. Схема трубопровода с насосной подачей

Поскольку трубопровод не меняет своего диаметра, то скорости υ₀ и υ₁ согласно уравнению расхода (3.5) равны между собой, и

= .

Удельная энергия жидкости на входе в насос Н_вх.равна:

Н_вх.= Р = ^Р – Н₁ – h_тр₁ . (8.15)

Составим уравнение Бернулли для сечений 2-2 и 3-3:

0 + Р + = Н₂ + Р + 0 + hтр2 .

Удельная энергия жидкости на выходе из насоса Н_вых.равна:

Р Р

Н_вых.= + = Н₂ + + h_тр₂ . (8.16)

Подставив в (8.14) выражения для Н_вх.и Н_вых.(8.15) и (8.16), получим:

Н_н = Н₂ + Н₁ + Р ^Р +h_тр .

^Р

Поскольку Н₂ + Н₁ + ^Р = Н_ст , и h_тр = КQ^m, то полу-

чим:

Н_н = Н_ст + КQ^m. (8.17)

Сравнивая полученную формулу (8.17) с формулой (8.8), можно отметить их полную идентичность. Таким образом, напор, создаваемый насосом, равен потребному напору трубопровода:

Н_н = Н_потр.. (8.18)

Определение напора насоса с помощью зависимости (8.18) достаточно сложно, поэтому чаще прибегают к графическому методу расчета (рис. 8.11).

Рис. 8.11. График определения рабочей точки насосного трубопровода

Для этого на графике строят характеристику потребного напора трубопровода Н_потр = f(Q) и характеристику насоса Н_н = f(Q) . Точка пересечения этих зависимостей называется рабочей точкой гидросистемы и является графическим решением уравнения (8.18).

8.5. Примеры.

Задачи на расчет простого трубопровода можно разбить на три типа:

І тип. Даны расход жидкости Q в трубопроводе, все геометрические размеры (ℓ, d, ∆z), шероховатость труб, давление в конечном сечении (для всасывающих трубопроводов в начальном), и характеристика жидкости (плотность ρ и кинематическая вязкость ν). Местные сопротивления либо заданы коэффициентами Іζ или эквивалентными длинами ℓ_экв, либо оцениваются по справочным данным.

Требуется найти потребный напор Н_потр.

По Q, d и ν находится число Рейнольдса R_е и определяется режим течения жидкости.

При ламинарном режиме течения искомый напор определяется по формулам (8.8) и (6.9):

^m , где К⁼ ℓ , m = 1. Н_потр. = Н_ст + КQ

При турбулентном режиме задача решается с помощью формул (8.8) и (8.4):

^m , где К = (λ_т ℓ + ζ_м) , m = 2. Н_потр. = Н_ст + КQ

ІІ тип. Даны: напор Н_расп, который будем называть располагаемым, и все величины, перечисленные в І типе задач, кроме расхода Q. Так как число Рейнольдса в данной задаче подсчитать нельзя, то необходимо выразить расход Q через критическое число Рейнольдса R_е = 2300 и определить Н_кр, соответствующее смене режима. Сравнив

Н_кр и Н_расп, можно легко определить режим течения.

При ламинарном режиме задача решается просто, как и в задаче І типа.

При турбулентном режиме задача решается по формулам (8.8) и (8.4).

В уравнении (8.4) содержатся два неизвестных (Q и λ_т), зависящие от числа Рейнольдса. Для решения задачи задают значение коэффициента λ_т с учетом шероховатости и определяют его по формуле Альтшуля при R_е → :

λ_т = 0,11 ^∆ d .

Значение коэффициента Дарси изменяется в небольших пределах (λ_т = 0,015…0,04).

Затем, решая уравнения (8.8) и (8.4), находят расход Q в первом приближении. По найденному расходу Q определяют R_е в первом приближении, а по R_е - уже более точное значение λ_т. Обычно бывает достаточно второго приближения.

Для решения этой же задачи графическим способом строят кривую потребного (располагаемого) напора для данного трубопровода с учетом переменности λ_т, то есть для ряда значений Q подсчитывают υ, R_е, λ_т и Н_потр по формуле (8.8). Затем, построив кривую Н_потр = f(Q), и зная ординату Н_потр = Н_расп, находят соответствующую ей абсциссу, то есть находят расход Q.

ІІІ тип. Даны расход Q, располагаемый напор Н_расп, и все величины, перечисленные ранее, кроме диаметра трубопровода d, который и нужно определить.

Так как число Рейнольдса определить нельзя, то выражают диаметр через критическое число Рейнольдса R_е = 2300 и определяют Н_кр, соответствующее смене режима движения жидкости. Сравнивая Н_кр и Н_расп, определяют режим течения.

При ламинарном режиме задача решается просто по формулам (6.9) и (8.8).

При турбулентном режиме задачу решают графически. При этом задаются рядом значений диаметра d и по ним подсчитывают Н_потр. Затем строят график Н_потр= f(d) и по нему, зная Н_расп, определяют диаметр d.

Если трубопровод состоит из n последовательно соединенных участков, то справедливы равенства:

_h_трQ = Q^Q_h.

При параллельном соединении n трубопроводов:

QQ ,

где Q – расход в точке разветвления.

8.5.1. На рисунке показан всасывающий трубопровод гидросистемы. Длина трубопровода ℓ = 1м, диаметр d = 20 мм, расход жидкости Q = 0,314 л/с, абсолютное давление воздуха в бачке р₀ = 100 кПа, высота Н = 1м, плотность жидкости ρ = 900 кг/м³. Определить абсолютное давление перед входом в насос при температуре рабочей жидкости t = 25°С (ν = 0,2·10^-4 м²/с). Как изменится искомое давление в зимнее время, когда при этом же расходе температура жидкости упадет до -35°С (ν = 10·10^-4 м²/с).

Составим уравнение Бернулли для сечений 1-1 и 2-2, проведя плоскость сравнений по оси горизонтального участка трубы:

Н + + 0 = 0 + + + hтр .

Определим скорость течения жидкости в трубе υ₁ из уравнения

расхода (3.5):

· ,

υ = = = _{,
· ,} = 1 м/с.

Определим число Рейнольдса:

· ,

R_е= = = 1 000.

Режим движения жидкости ламинарный (α=2), поэтому потери h_тр определяются по формуле Пуазейля (6.9):

ℓ · , · · ,

hтр = Q = , · , · , = 0,16 м.

Выразим абсолютное давление р₁ перед входом в насос из составленного для сечений 1-1 и 2-2 уравнения Бернулли:

· ·

р₁ = Нρg + р₀ – ρ – h_трρg = 1·900·9,8 + 100 000 – –

– 0,16·900·9,8 = 106,5 кПа.

Подсчитаем потери напора при t = –35°С:

· , · · , h_тр = , · , · , = 8,16 м.

Тогда искомое давление при при t = –35°С:

· ·

р₁ = 1·900·9,8 + 100 000 – – 8,16·900·9,8 = 36 кПа.

8.5.2. По трубопроводу диаметром d = 10 мм и длиной ℓ = 10 м подается жидкость с вязкостью ν = 0,0001 м²/с под действием перепада давления ∆р = 4 МПа; плотность ρ = 1000 кг/м³. Определить режим течения жидкости в трубопроводе.∆ρg

Определим расход жидкости в трубопроводе. Поскольку потери в трубопроводе будут равны разности пъезометрических высот, то с учетом формулы Пуазейля:

ℓ ∆

hтр = Q = = , откуда

∆ · , · ,

Q = = = 0,98 л/с. ℓ · , · ·

Теперь определим расход Q_кр при критическом значении числа Рейнольдса R_е = 2300:

υ = = , откуда

е кр · , · , · ,

Q_кр = = = 1,8 л/с.

Поскольку Q < Q_кр, значит режим течения жидкости – ламинарный.

8.5.3. Определить потребный напор, который необходимо создать в сечении О-О для подачи в бак воды с вязкостью ν = 0,008 м²/с, если длина трубопровода ℓ = 80 м; его диаметр d = 50 мм; расход жидкости Q = 15 л/с; высота Н₀ = 30 м; давление в баке р₂ = 0,2 МПа; коэффициент сопротивления крана ζ₁ = 5; колена ζ₂ = 0,8; шероховатость стенок трубы ∆ = 0,04 мм.

Составим уравнение Бернулли для сечений О-О и 1-1 относительно плоскости сравнения, совпадающего с сечением О-О:

0 + + = Н0 + + 0 + hдл + hм .

Определим число Рейнольдса, воспользовавшись уравнениями

(3.5) и (5.5):

· ,

R_е = = = 477 707.

, · , · ,

Поскольку режим течения турбулентный (α = 1), то потери напора по длине определим по формуле Дарси-Вейсбаха (6.6): ℓ h_дл = λ_т .

Скорость течения жидкости:

· ,

υ = = _{,
· ,} = 7,64 м/с.

Коэффициент Дарси по формуле Альтшуля (6.12):

∆ , ,

λ_т = 0,11 + = 0,11 + = 0,019. е

· ,

Тогда h_дл = 0,019· = 90,5 м.

, · ,

Местные потери напора (с учетом внезапного расширения ζ_р) равны:

h_м =(ζ₁ + 4ζ₂+ζ_р) = (5 + 4·0,8 +1) · = 27,4 м.

· ,

Тогда потребный напор равен:

Н_потр = = Н = 30 + + 90,5 + 27,4 – =

= 165,7 м.

8.5.4. Определить расход в трубе для подачи воды (вязкость ν = 0,01 Ст) на высоту Н = 16,5 м, если диаметр трубы d = 10 мм, ее длина ℓ = 20 м, располагаемый напор в сечении трубы перед краном

Н_расп = 20 м, коэффициент сопротивления крана ζ₁ = 4, колена ζ₂ = 1. Трубу считать гидравлически гладкой.

Уравнение Бернулли для сечений 1-1 и 2-2 относительно плоскости сравнения, совпадающей с горизонтальной осью трубы, будет иметь вид:

ат ат

0 + + = Н + + 0 + ∑h_тр , или

+ = Н + ∑hтр .

Располагаемый напор Н_расп будет равен:

Н_расп = = Н + h_тр − .

Выразим скорость υ1 из уравнения расхода (3.5) и подставим в

скоростной напор . Тогда:

Н_расп = Н + h_тр − = Н + h_тр– .

Гидростатический напор в данном случае равен высоте Н (Н_ст = Н).

Потери напора h_тр = КQ^m, где К = (λ ℓ + ζ_м) .

Местные потери напора будут равны:

∑ h_м = (ζ_кр + ζ_пов + ζ_р) = (4 + 1 + 1) = 6.

С учетом уравнения (8.8) можно записать, что:

^m= Нрасп –Нст + = 20 – 16,5 + = 3,5 + .

КQ

Предположим, что режим движения жидкости – турбулентный (α = 1). Тогда в этом уравнении две неизвестных – Q и λ_т. Решим задачу методом последовательных приближений, задавая значение λ_т (λ_т находится в пределах 0,01 – 0,04). Пусть λ_т = 0,03, тогда, выразив число Рейнольдса R_е из формулы Блазиуса (6.11) для гидравлически гладких труб, получим:

R_е = = 12 310 > R_е.кр= 2300.

Предположение о турбулентном режиме движении жидкости верно. Тогда уравнение для потерь напора будет выглядеть так:

hтр = КQ^m– = (λ_т +∑ h_м – α) = 3,5 м.

Определим скорость υ и расход Q при R_е = 12310 (λ_т = 0,03): е · , · υ = = =1,23 м/с.

, · , м³/с. Тогда: Q = υ =1,23· = 0,096·10

(λт +∑ hм – α) = (0,03 , + 6 – 1) , · , , · · , = 4,96 м, что не соответствует разности Н_расп –Н_ст = 20 – 16,5 = 3,5 м.

Примем значение λ_т = 0,032, тогда:

R_е = 9509; υ = 0,95 м/с; Q = 0,075· м³/с.

3,5.

Примем значение λ_т = 0,0316, тогда:

R_е = 10 000; υ = 1 м/с; Q = 0,078· м³/с.

= 3,5 = Нрасп –Нст .

Итак, методом последовательных приближений значение расхода Q = 0,078·10 м³/с.

Решим эту же задачу графическим методом. Для этого построим зависимость Н_потр = f(Q). Выберем ряд значений для расхода Q. Результаты расчетов сведем в таблицу:

Q, × 10м³/с	υ = ^4Q πd , м/с	R_е=	, λт = , _е	Нпотр = Нст + m – ,м КQ
0,05	0,64	6400	0,035	18
0,07	0,89	8900	0,0325	19,34
0,09	1,14	11 400	0,03	20,86
0,11	1,40	14 000	0,029	22,8
0,13	1,65	16 500	0,0278	25
0,15	1,91	19 100	0,0269	27,5

Из построенного графика видно, что при располагаемом напоре Н_расп = 20 м расход жидкости составит Q = 0,078 л/с.

8.5.5. При каком диаметре трубопровода подача насоса составит Q = 1 л/с, если на выходе из него располагаемый напор Н_расп = 9,6 м; длина трубопровода ℓ = 10 м; эквивалентная шероховатость ∆ = 0,05 мм; давление в баке р₀ = 30 кПа; высота Н₀ = 4 м; вязкость жидкости ν =0,015 Ст (0,0000015 м²/с) ; плотность ρ = 1000 кг/м³? Местными гидравлическими сопротивлениями в трубопроводе пренебречь. Учесть потери при входе в бак.

Располагаемый напор будет равен:

Нрасп = Нст + hтр – , где Нст = Н0 + = 4 + = 7 м,

hтр = λ d^ℓ+ ζм 2^υg , где ζм = 1 − = 1, т. к. S₂ S₁ .

Тогда можно записать, что:

hтр = λ dℓ + 1 2υg = Нрасп – Нст + . ℓ

Поскольку υ = = , то h_тр = (λ + 1 – α) = 2,6 м.

Определим режим течения жидкости. Для этого определим диаметр d при R_е = 2300, и воспользовавшись формулой Пуазейля (6.9), сравним получаемый напор с заданным:

d = = = 0,37 м. е

ℓ h_тр = Q = = 0,0000033 2,6 м.

Режим течения, определяемый расходом Q =1 л/с, будет турбулентным (α = 1). Итак:

ℓ

h_тр = λ = 2,6 м,

∆ ,

λ_т = 0,11 + . е

Решим задачу графически. Для этого, задаваясь значениями d, определим разность напоров Н_расп – Н_ст .

d, мм	Rе =	∆ λт=0,11 + , е	Н_расп–Н_ст= = λ ℓ
10	85 000	0,03	248,1
15	56 600	0,0285	31
20	42 500	0,0278	7,66
25	34 000	0,0276	2,36
30	28 300	0,0277	0,95
35	24 290	0,028	0,45

Для более точного построения графика зададим дополнительные значения диаметра d:

21	40 440	0,0277	5,7
22	38 636	0,02772	4,4
23	36 956	0,02768	3,6
24	35 386	0,02767	2,9

По полученным данным строим график зависимости

Н_расп – Н_ст = f(d):

При Н_расп – Н_ст = 2,6 м диаметр d = 24,5 мм.

8.5.6. Трубопровод с расходом жидкости Q = 0,32 л/с в точке М разветвляется на два трубопровода: первый размерами ℓ₁ = 1,0 м; d₁ = 10 мм; второй размерами ℓ₂ = 2,0 м; d₂ = 8 мм. В точке N эти трубопроводы смыкаются. Во втором трубопроводе установлен фильтр Ф, сопротивление которого эквивалентно сопротивлению в трубе длиной ℓ_э = 200d₂. Определить расход и потерю давления в каждом трубопроводе при ρ = 900 кг/м³; ν = 1Ст.

Определим расход в каждом трубопроводе по формуле Пуазейля (6.9):

hтр = ℓ Q1 ; hтр = ℓ Q2 (ℓ2 + 200d2) .

Поскольку при параллельном соединении трубопроводов потери в них равны, то есть h_тр1 = h_тр2 , то после сокращения одинаковых величин получим:

ℓ (ℓ )

= .

Q₁ = 8,79·Q₂ .

Сумма расхода в точке М в данном случае будет равна сумме расходов в параллельных трубопроводах:

Q = Q₁ + Q₂ = 8,79·Q₂ + Q₂ .

Q₂ = = 0,0327 л/с.

Q₁ = 8,79·Q₂ = 0,287 л/с. Потери давления:

∆р₁ = ℓ Q₁= 105 кПа.

∆р₂ = ℓ Q₂(ℓ₂ + 200d₂) = 105 кПа.

8.5.7. Контрольные вопросы.

1. В чем разница между простым и сложным трубопроводом?

2. Сформулируйте три задачи при расчете установившегося напорного движения в простых трубопроводах.

3. На основе каких уравнений решаются указанные основные задачи?

4. Как выражается напор при истечении в атмосферу и под уровень?

5. Что такое характеристика потребного напора?

6. В чем отличие характеристики потребного напора при ламинарном и турбулентном режимах движения жидкости?

7. В чем отличие определения расхода и потерь напора при различных соединениях простых трубопроводов?

8. По какому методу рассчитывают сложные трубопроводы?

9. Определите цель расчета трубопровода с насосной подачей.

10. Что такое рабочая точка насосного трубопровода?

Раздел 9 Основы гидропневмопривода

9.1 Общие сведения.

Гидравлическим (пневматическим) приводом называется совокупность гидравлических (пневматических) машин, аппаратов и линий, служащих для передачи энергии и преобразовании движения выходного звена посредством рабочей среды (жидкости в гидроприводе и сжатого воздуха в пневмоприводе).

Практически нет такой области деятельности человека, где бы не использовались гидравлические или пневматические системы. Это станкостроение, строительное и дорожное машиностроение, судостроение, металлургия и автомобилестроение, пищевая промышленность и т. д. Современное развитие техники позволяет более широко внедрять гидравлические и пневматические приводы. Например, если до недавнего времени в автомобилестроении применение гидро- и пневмосистем ограничивалось в основном тормозной системой, системой охлаждения, системами смазки и подачи топлива, то в настоящее время появился целый ряд гидропневмосистем. Это гидравлическое переключение скоростей в механической коробке передач, регулирование уровня дорожного просвета, гидравлическая регулировка света фар, гидроусилитель руля, система экстренного торможения и т. д.

По существу действия гидропневмопривод является устройством, преобразующим энергию движущейся жидкости (гидропривод) и сжатого воздуха (пневмопривод) в механическую энергию. Действие гидропневмопривода основано на законах равновесия и движения рабочей среды. Выбор того или иного привода машины во многом определяется учетом его особенностей.

9.2 Гидравлический привод.

Широкое применение гидроприводов объясняется рядом их существенных преимуществ перед другими типами приводов. К основным преимуществам гидроприводов можно отнести:

- возможность получения больших усилий при ограниченных размерах гидродвигателей;

- широкий диапазон бесступенчатого регулирования скоростей;

- большая плавность работы и малая инерционность;

- возможность преобразования гидравлической энергии практически в любой вид движения.

Гидроприводы имеют и недостатки, снижающие область их применения. Это потери на трение и утечки, снижающие КПД гидропривода и вызывающие нагрев рабочей жидкости. Необходимость применения фильтров тонкой очистки повышает стоимость гидроприводов и усложняет техническое обслуживание. Изменение вязкости масла при его нагреве приводит к изменению скорости движения рабочих органов. Узлы гидропривода весьма трудоемки в изготовлении, а для его обслуживания требуется специалист – гидравлик.

Гидравлические приводы реализуют свою работу за счет энергии потока рабочей жидкости. Удельная энергия потока жидкости (энергия единицы веса объема жидкости) определяется уравнением Бернулли (4.17). Передачу энергии жидкостью можно осуществлять путем изменения любого из членов этого уравнения.

В зависимости от вида используемой в гидромашинах энергии гидравлические приводы делят на гидростатические (объемные) и гидродинамические.

Гидростатический (объемный) привод. В этом приводе гидромашины в основе своего действия используют потенциальную

энергию жидкости ( ρg), которая легко преобразуется в механиче-

скую работу с помощью гидродвигателей (например, гидроцилиндров). Доля геометрического напора (z) и кинетической энергии ^υ 2g для этих приводов не превышает 1-1,5% полной энергии

жидкости.

Гидравлический привод, использующий потенциальную и кинетическую энергию движения жидкости ρg + ^υ 2g , называет-

ся гидродинамическим.

Использование различных видов энергии объемным и гидродинамическим приводом объясняется применением различных конструкций гидромашин. В объемном гидроприводе используются объемные гидромашины, в гидродинамическом – лопастные.

Принцип действия объемной гидромашины основан на попеременном заполнении рабочей камеры жидкостью и вытеснении ее в напорную линию, то есть между всасывающей и напорной линией нет прямого сообщения.

В гидродинамических (лопастных) машинах взаимодействие рабочего органа машины с жидкостью происходит в проточной полости, постоянно сообщенной с входом и выходом гидромашины.

Принцип действия объемного гидропривода основан на использовании двух главных свойств рабочей жидкости. Во первых, жидкость практически несжимаема, во вторых, она обладает свойством передавать давление по всем направлениям без изменения (закон Паскаля).

Работу объемного гидропривода рассмотрим на примере простейшей гидропередачи – гидравлического домкрата (рис. 9.1).

Рис. 9.1. Схема гидравлического домкрата:

1 – малый гидроцилиндр (насос); 2 – плунжер; 3 - большой гидроцилиндр (гидродвигатель); 4 – поршень;5 – рычаг; 6 – напорная гидролиния

В соответствии с законом Паскаля, пренебрегая при этом гидравлическими сопротивлениями, разностью масс плунжера и поршня, а также трением плунжера и поршня в цилиндрах, заключаем, что давление в цилиндре 1 (р₁ = F₁S₁) и в цилиндре 3 (р₂ = F₂S₂) будут одинаковы:

р = F₁S₁ = F₂S₂ , (9.1) где S₁ и S₂ – рабочая площадь плунжера и поршня.

Сила F₁ определяется силой G, действующей на рычаг 5, и отношением длин рычага а и b:

F₁ = G (а + b) b .

Поскольку жидкость несжимаема, то вытесненные объемы жидкости W в цилиндрах 1 и 3 и расходы жидкости Q на основании уравнения неразрывности потока (3.5) будут равны между собой:

W = h₁S₁ = h₂S₂ , (9.2) Q = υ₁S₁ = υ₂S₂ , (9.3)

где h₁ и h₂ - перемещения плунжера и поршня в цилиндрах; υ₁ и υ₂ - скорости перемещения плунжера и поршня.

Полезная мощность, развиваемая при перемещении плунжера 2 в цилиндре 1, равна N₁ = F₁υ₁. В идеальном случае (без учета потерь) она должна быть равна мощности, передаваемой поршню 4 цилиндра

3 (N₂ = F₂υ₂), то есть:

N = F₁υ₁= F₂υ₂. (9.4)

Выразим скорость из уравнения расхода (3.5) и подставим ее в уравнение (9.4). Тогда мощность данного гидропривода будет равна:

N = Q = Q = рQ . (9.5)

Как видно из уравнения (9.5), полезная мощность гидропривода пропорциональна давлению р и расходу Q рабочей жидкости, то есть увеличение мощности гидропривода можно произвести либо за счет роста давления р, либо расхода Q.

Увеличение давления за счет расхода жидкости нерационально, поскольку увеличение расхода Q возможно только за счет увеличения скорости течения жидкости υ (9.3). Рост скорости υ течения жидкости ведет к резкому увеличению потерь давления ∆р. Потери давления ∆р = ρg∆h определяются разностью пъезометрических высот ∆h [п. 6.1], или потерями напора. Потери напора определяются формулами (6.2) и (6.6), то есть потери давления ∆р в гидроприводе пропорциональны квадрату скорости, и в конечном итоге – квадрату расхода (в общем случае).

Увеличение мощности объемного гидропривода осуществляется только за счет увеличения давления, однако это ведет к удорожанию всей системы.

В реальности за счет сил трения в уплотнениях плунжера и поршня, наличия сил вязкости жидкости и инерции подвижных частей гидропривода, загрязнения рабочей жидкости ее нагрева в процессе эксплуатации, утечек жидкости подводимая мощность N₁ и мощность на выходе N₂ гидропривода не равны между собой. Их отношение определяет коэффициент полезного действия η гидропривода:

η = N N. (9.6)

Понятие "гидросистема" включает в себя собственно гидросистему и гидропривод. В отличие от гидропривода для гидросистем, обеспечивающих подачу жидкости к потребителю, характерно отсутствие устройств, преобразующих энергию жидкости в механическую работу. К таким системам относятся: системы водоснабжения, системы жидкостного охлаждения и смазывания различных машин, а также системы подачи смазочно – охлаждающих жидкостей (СОЖ) металлорежущих станков и др.

Гидродинамическими передачами (ГДП) называют такие передачи, в которых в качестве насоса и двигателя используются лопастные машины.

Взаимодействие лопастных гидромашин с потоком жидкости обеспечивается за счет лопаток, установленных на рабочем колесе или непосредственно на валу вращения, причем это взаимодействие достаточно эффективно при значительных скоростях движения жидкости и рабочего колеса.

Если на входе и выходе лопастного насоса установить пъезометры, то разность уровней высот этих пъезометров определит то полезное давление, которое насос передает движущейся жидкости

(рис.9.2).

Рис. 9.2. Схема работы лопастного насоса

Величина Н_н будет называться напором насоса. Напор насоса Н_н – это энергия, сообщаемая насосом единице веса жидкости, или разность удельных энергий жидкости на выходе и входе насоса. Тогда полезная мощность насоса N_пн будет равна произведению силы давления ∆рS на скорость перемещения жидкости υ:

N_пн = ∆рS_нυ = ρgН_нQ_н , (9.7) где S_н - площадь проходного сечения насоса, Q_н - подача насоса.

Реальная мощность насоса N_н будет больше полезной мощности N_пн на величину потерь, которые оцениваются КПД насоса η_н:

η_н = N^пн _N_н. (9.8)

С учетом выражения (9.8) мощность насоса N_н будет равна:

N_н = ρgН^нQ^н η_н. (9.9)

Если жидкость отдает энергию лопастному колесу, и эта энергия потока жидкости переходит в механическую энергию на валу, на котором установлено это колесо, то данная гидромашина будет называться лопастным гидродвигателем или гидравлической турбиной.

Рассмотрим работу ГДП, изображенной на рис. 9.3.

Энергия потока жидкости, создаваемого насосным колесом Н, которое приводится во вращение посторонним источником механической энергии, передается на турбину Т, что приводит ее во вращение. После насоса и перед турбиной располагаются неподвижные реакторы Р_н и Р_т, которые служат для направления потока жидкости. Так как входной и выходной валы жестко не связаны между собой, они имеют разные моменты и угловые скорости. При протекании жидкости в трубопроводах 1 и 2 происходят значительные потери энергии жидкости, которые обусловлены вязкостью и скоростью движения жидкости, а также шероховатостью стенок каналов и размерами трубопроводов.

Рис. 9.3. Принципиальная схема гидродинамической передачи:

Н – насос; Т – турбина; Р_н – направляющий аппарат реактора насоса; Р_т – направ-

ляющий аппарат реактора турбины; 1,2 – трубопроводы

Рис. 9.4. Гидродинамические передачи Феттингера:

а - гидротрансформатор; б - гидромуфта; Н - насос; Т - турбина; Р - реактор

В 1902 г. немецкий инженер Феттингер предложил объединить в одном корпусе насосное, турбинное колесо и реактор. Такая ГДП была названа гидродинамическим трансформатором (ГДТ), способным передавать мощность от ведущего вала к ведомому с трансформацией крутящего момента (рис. 9.4, а). Для повышения экономичности из ГДТ был изъят реактор. Так появилась новая ГДП, получившая название гидродинамической муфты (ГДМ), передающая мощность от ведущего вала к ведомому без трансформации крутящего момента (рис. 9.4, б).

Рассмотрим процесс воздействия потока жидкости, создаваемого насосным колесом, на твердую преграду (турбинное колесо). При этом пренебрежем потерями напора и неравномерностью распределения скоростей в сечениях потока (α = 1).

Поток жидкости оказывает динамическое воздействие на преграду, находящуюся на ее пути. Это воздействие особенно велико, если преграда расположена на участке компактной струи. Для сравнения рассмотрим воздействие такой компактной струи на твердую преграду в виде плоской поверхности и на криволинейную поверхность.

Воздействие струи на твердую плоскую преграду, перпендикулярную оси струи. Пусть на плоскую преграду набегает струя жидкости некоторой ширины, имеющая скорость υ₀ (рис. 9.5). При ударении происходит симметричное растекание жидкости по поверхности. Будем считать, что струя жидкости делится на два симметричных потока.

Рис. 9.5. Схема воздействия струи жидкости на плоскую преграду:

m₀, m₁, m₂ – масса жидкости; υ₀, υ₁, υ₂ –скорость течения струи в сечениях 0-0, 1-1

и 2-2; р – сила воздействия струи на преграду; R – реактивная сила; α – угол между осью Х и направлением течения струи жидкости

Выделим сечениями 0-0 и 1-1и 2-2 некоторый объем жидкости и применим к нему закон изменения количества движения. Напишем уравнение количества движения применительно к данному случаю:

d(mυ_i) = Rt = m₁υ₁+ m₂υ₂ – m₀υ₀,

где m – масса жидкости; υ₀ – скорость потока до его воздействия на преграду; υ₁ и υ₂– скорости после воздействия на преграду; t – время воздействия; d(mυ_i) – изменение количества движения.

Реактивная сила R равна силе давления р, направленной в противоположную сторону:

рt = m₀υ₀– m₁υ₁ – m₂υ₂ .

Изменение количества движения в данном случае равно импульсу силы давления р на преграду, и в проекции на ось Х будет равно:

рt = m₀υ₀ – m₁υ₁cosα – m₂υ₂cosα . (9.10) Поскольку α = 90°, то cosα = 0, и тогда

р = = ρQυ₀. (9.11)

Если плоская преграда перемещается со скоростью υ_п, совпадающей с направлением движения струи, то можно записать:

р = ρQ(υ₀ – υ_п). (9.12)

Воздействие струи на криволинейную поверхность. В случае симметричной криволинейной поверхности α₁ = α₂ = α > ^π 2 (рис 9.6).

Рис. 9.6. Схема воздействия струи на симметричную криволинейную поверхность

При m₁υ₁ = m₂υ₂ = 0,5m₀υ₀ уравнение (9.10) предстанет в виде: рt = m₀υ₀ – 2m₁υ₁cosα = m₀υ₀(1 – cosα).

р = ^{(
– )} = ρQυ₀(1 – cosα). (9.13)

Если угол α = 180°, то cosα = –1, и уравнение (9.13) примет вид:

р = 2ρQυ₀. (9.14)

При сравнении формул (9.14) и (9.11) видно, что сила воздействия струи на криволинейную поверхность возрастает в два раза по сравнению с силой р, действующей на плоскую стенку. Это свойство используется при создании рабочих колес турбин. На ободе колеса такой турбины расположены лопасти с криволинейной поверхностью.

Поскольку струя жидкости воздействует на движущееся с некоторой окружной скоростью υ_к лопатку турбины, то уравнение (9.14) примет вид:

р = 2ρQ(υ₀ – υ_к). (9.15)

Мощность N, отдаваемая струей жидкости рабочему колесу турбины, будет равна произведению силы давления р на скорость перемещения лопаток колеса υ_к:

N = 2ρQ(υ₀ – υ_к) υ_к. (9.16)

При υ_к = 0, когда колесо неподвижно, мощность N = 0; при υ_к= υ₀ точки колеса имеют ту же скорость, что и поток жидкости, то есть нет никакого силового воздействия потока на колесо и N = 0. Очевидно, что при каком-то значении υ_к колесо турбины получит максимальную мощность. Для этого надо взять производную от мощности N по скорости υ_к, приравнять ее нулю и найти соответствующее значение υ_к:

dN dυк= 2ρQυ0 - 4ρQυк = 0, откуда υк = = υ0 .

Итак, если окружная скорость колеса υ_к = 0,5υ₀ , то турбина получает от потока жидкости максимальную мощность:

N = = = Е_к . (9.17)

Из формулы (9.17) видно, что в турбинах с криволинейной формой лопаток используется вся кинетическая энергия потока жидкости.

9.3. Пневматический привод.

Объемный пневматический привод – это устройство, преобразующее энергию сжатого воздуха в механическую энергию.

К основным достоинствам пневмоприводов относят:

- надежность и долговечность;

- быстрота срабатывания;

- простота и экономичность;

- пожаробезопасность и нейтральность рабочей среды.

В пневматических устройствах рабочим телом является сжатый воздух (смесь газов); он используется как в силовых системах (пневмопривод), так и для целей управления (пневмоавтоматика).

Газ – одно из агрегатных состояний вещества, в котором его частицы не связаны между собой молекулярными силами притяжения и хаотично движутся, заполняя весь предоставленный им объем. С точки зрения механики жидкости и газы различаются только сжимаемостью.

Произведение полезного объема на среднее давление газа в рабочем диапазоне давлений определяет накопленную энергию резервуара.

Процессы сжатия и расширения газов подчиняются закону Бойля – Мариотта:

р₁W = р₂W, (9.18)

где W₁ и W₂ – объемы газа при постоянной температуре при давлениях р₁ и р₂ соответственно; n - степенной показатель.

Уравнение (9.18) связывает давление р₁ и объем W₁ в начале термодинамического процесса с аналогичными величинами (р₂и W₂) в конце него.

Если состояние газа изменяется медленно, то есть происходит полный теплообмен с окружающей средой, то такой процесс называется изотермическим. Температура газа при этом не меняется и n = 1.

При работе в адиабатном режиме теплообмена с окружающей средой не происходит. Такое состояние наступает тогда, когда сжатие или расширение газа протекает очень быстро, и в этом случае n = 1,4.

Рис. 9.6. Линии термодинамических процессов

Изменение состояния на практике происходит в зависимости от скорости течения газа в диапазоне между адиабатной и изотермической кривой (рис. 9.6). Такое изменение состояния называется политропным. Величина показателя n, который называется показателем политропы, изменяется от 1 до 1,4 (1 < n < 1,4).

9.4. Контрольные вопросы.

1. Перечислите преимущества и недостатки объемного гидропривода.

2. В чем отличие объемного и гидродинамического приводов?

3. Почему увеличение мощности объемного гидропривода осуществляется только за счет увеличения давления?

4. Что такое напор насоса?

5. Расскажите принцип работы гидродинамической передачи.

6. Когда кинетическая энергия потока жидкости в гидродинамической передаче используется полностью?

7. Расскажите о достоинствах пневматического привода.

8. Как определяется энергия сжатого воздуха в резервуаре?

9. Что такое политропный процесс изменения состояния газа (воздуха)?

Приложение 1 Схема к уравнению Бернулли

Приложение 2 Схема к определению потерь напора в круглых трубах.

Список рекомендуемой литературы.

1. Башта М. и др. Гидравлика, гидромашины, гидроприводы, - М.: Машиностроение, 1982 г. - 423 с.

2. Стесин С. П. и др. Гидравлика, гидромашины и гидропневмопривод, - М.: Академия, 2005 г. – 336 с.

3. Лепешкин А. В. Гидравлические и пневматические системы, - М.: Академия, 2005 г. – 336 с.

4. Некрасов Б. Б. и др. Задачник по гидравлике, гидромашинам и гидроприводу, - М.: Высшая школа, 1989 г. – 192 с.

137

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.