
Публикация является частью публикации:
Задачи на геометрические прогрессии - простые задачи
Легкий уровень
№1. Найдите знаменатель q геометрической прогрессии (an), для которой a1=5, a2=15
№2. Найдите сумму бесконечной геометрической прогрессии (an), определенной a1=1 и q=12
№3. Пусть (an) есть геометрическая прогрессия, определенная a1=1 и q=5. Найдите сумму a1+a2+a3+a4+a5
№4. Пусть (an) есть геометрической прогрессией, такой что a1=2 и q=3. Найдите сумму первых пяти элементов.
№5. Пусть (an) - возрастающая геометрическая прогрессия. Если a1=2 и a5=162, определите a3
№6. (an) -геометрическая прогрессия. Если a1=5 и a2=10, найдите a6
№7. Пусть (an) - геометрическая прогрессия со знаменателем q=13. Если a4=12, найдите a1.
№8. Найдите четвертый член геометрической прогрессии (an), для которой a1=2 и q=3.
№9. Найдите знаменатель q переменной геометрической прогрессии (an), для которой a1=125, a2=−25 и a3=5.
№10. Определите знаменатель q геометрической прогрессии (an), для которой a1=5 и a4=−40
№11. Определите знаменатель q увеличивающейся геометрической прогрессии (an), для которой a1=5 и a3=20.
№12. Найдите знаменатель q геометрической прогрессии (an), для которой a1=−1, a2=5
№13. Определите значение a3, если (an)есть геометрическая прогрессия и a4-a2=18, a5 –a3=36.
Средний уровень
№1. Дана геометрическая прогрессия (an), для которой a1=15 и q=−4. Найдите ее шестой член.
№2. Найдите второй член геометрической прогрессии (an), которые удовлетворяет условию a2+a5 –a4=10, a3+a6 – a5=20.
№3. Найдите 0,272727(27) в виде дроби.
№4. Сумма членов бесконечной геометрической прогрессии есть S1=6. Сумма квадратов всех членов той же прогрессии S2=18. Найдите первый член этой прогрессии.
№5. Определите знаменатель q геометрической прогрессии (an), для которой a1=1 и S4=40
№6. Найдите знаменатель q геометрической прогрессии (an), для которой S=15 и a1=9
№7. Найдите знаменатель q бесконечной геометрической прогрессии (an), для которой S=7 и a1=4
№8.
Найдите сумму первых четырёх членов геометрической прогрессии (an), для которой an=![]() .
.
№9.
Найдите сумму бесконечной геометрической прогрессии, явно определённой an=![]() .
.
№10.
Найдите сумму бесконечной геометрической прогрессии (an)=![]() .
.
№11.
Найдите произведение первых 7 членов геометрической прогрессии (an), определённой
как: a1=![]() , q=11.
, q=11.
№12. Пусть (an) есть переменной геометрической прогрессией. Если a1=5 и a7=405. Чему равно a4?
№13. Найдите сумму первых 5 степеней 7.
№14. Пусть (an) есть геометрической прогрессия, определённая a1=2 и q=−2. Найдите сумму её первых 10 элементов.
№15. Пусть x1, x2 будут корнями произведения x2−3x+a=0 и y1, y2 будут корнями произведения x2−12x−b=0. Если x1, x2, y1, y2 образуют возрастающую геометрическую прогрессию в указанном порядке определения значения a, b.
Сложный уровень
№1. Дана последовательность, определённая как a1=1;an+1−an=3n, найдите значение a10.
№2. a,b,c является геометрической прогрессией (a,b,c - действительные числа). Если a+b+c=26 и a2+b2+c2=364, найти b.
№3. Найдите
бесконечную сумму S=1+2.![]() +3.
+3.![]() )2+...+(n+1).(
)2+...+(n+1).(![]() )n+...
)n+...
391)
Найдите знаменатель бесконечной геометрической прогрессии,
если известно, что ее сумма равна 18, а ее первый член равен 12.
392) Найдите первый член геометрической прогрессии, если
известно, что сумма 6 первых ее членов равна 6552, а знаменатель равен 3.
393) Найдите знаменатель геометрической профессии, если
известно, что сумма 4 се первых членов равна 8736, а се первый член равен 56.
394) Найдите третий член бесконечной геометрической прогрессии,
если известно, что ее сумма равна 66, а се первый член равен 33.
395) Найдите четвертый член геометрической прогрессии, если
известно, что сумма 5 ее первых членов равна 713, а ее знаменатель равен 2.
398) Первый член бесконечной убывающей геометрической прогрессии
равен 8, а ее сумма равна 16. Найдите сумму третьего и четвертого членов этой
геометрической прогрессии.
399) Третий член геометрической профессии с положительным
знаменателем равен 9, а сумма первого члена со вторым равна 4. Найдите пятый
член этой геометрической прогрессии.
400) В геометрической прогрессии с положительным знаменателем
третий член равен 4, а пятый 16. Найдите сумму первых 10 членов этой
геометрической прогрессии.
советую знать 2 способа решения задачи. В 1-ом способе решения, вам нужно узнать лишь знаменатель прогрессии q, который находим делением последующего члена на предыдущий, например, q=1:2=1/2. Значит получается, что каждый следующий член получается делением на 2, их легко угадать: 1/2, 1/4. Затем просто складываем все члены прогрессии и получим ответ 7,75. Во втором способе нужно знать формулу суммы n первых членов геометрической прогрессии S(n), где n-это количество членов прогрессии. Данной формулой есть смысл пользоваться,лишь при большом количестве членов геометрической прогрессии.

В данной задаче на арифметическую прогрессию, мы вначале находим разность d, где из последующего члена отнимаем предыдущий, получим 4. Далее найдем a11 по любой из 3 формул, ответом будет 46.

Следующая задача ГИА по математике 2014 похожа на предыдущую, но здесь вначале надо найти 2-ой член арифметической прогрессии по формуле. Затем находим разность d и 10-ый член прогрессии.

Данная задача гиа по математике на арифметическую прогрессию требует найти сумму первых пятидесяти членов арифметической прогрессии. Для этого как обычно находим разность d, затем 50-ый член прогрессии. В конце решения подставляем готовые числа в формулу суммы и находим ответ 2100.

Простое задание на арифметическую прогрессию, находим разность, а затем нужный член.

В этом задании ГИА по математике мы поочередно подставляем натуральные числа: 1,2,3 и т.д. в формулу вместо буквы n. Считаем результаты и находим, что число 7/2 является членом последовательности.

В начале решения задачи на арифметическую прогрессию, выражение с формулой преобразуем в неравенство большое единицы. Решая неравенство, находим, что n<5,5 и значит n=5, поскольку в условии n - это натуральные числа.

Еще одна интересная задачка на арифметическую прогрессию, когда известны 2 члена, причем не порядковых. В начале мы, как всегда, находим разность d, выражая больший член через меньший, решаем уравнение и получаем d=5. Затем, используя формулу суммы членов арифметической прогрессии, находим S4, предварительно найдя a4 равное 23. Подставим числа в формулу, получим в ответе 62.

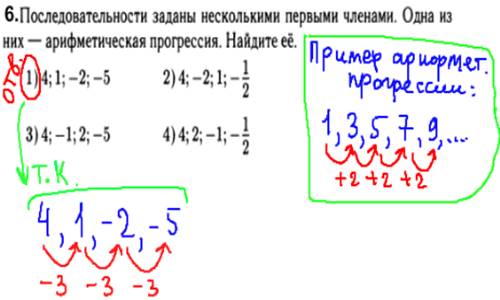
Простое задание, здесь нужно знать, что арифметическая прогрессия - это последовательность чисел, изменяющихся на одно и тоже число (т.е. одинаковое число прибавляется, либо отнимается). Таким образом, верный вариант ответа - 1), т.к. там всё время отнимается число 3.
В этом задании гиа 2014, мы подставляем вместо буквы n число 11, проверкой убеждаемся, что 4)-ый вариант ответа нам подходит, т.к. -14 меньше -11.

Рассмотрим задание ГИА по математике 2014 на геометрическую прогрессию. В задаче нужно найти сумму первых пяти членов геометрической прогрессии. Для этого вначале мы находим знаменатель q=b2/b1 или b3/b2, получим число 3. Затем вспоминаем формулу суммы членов геометрической прогрессии Sn=b1*(qn-1)/(q-1), подставим туда значения первого члена и знаменателя, получим в ответе 242.

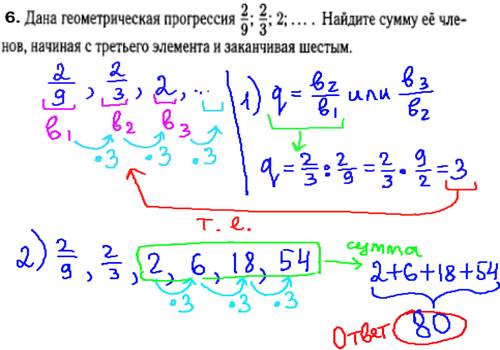
В данной задаче по алгебре на геометрическую прогрессию самым главным является нахождение знаменателя q, равный отношению последующего члена на предыдущий. Знаменатель равен 2, на который умножаем каждый член геометрической прогрессии, получим 2/9, 2/3, 2, 6, 18, 54. Сумма со второго по шестой член равна 2+6+18+54=80.
В этой задаче ГИА по математике мы вначале находим знаменатель геометрической прогрессии q, где последующий член делим на предыдущий, получим q=-3. Затем по любой из 3-х формул находим седьмой член геометрической прогрессии b7, в ответе получим -243.

В этом задании ГИА 2014 вспоминаем понятие геометрической прогрессии - это последовательность чисел, где каждое последующее число увеличивается или уменьшается во сколько-то раз (т.е. умножаем или делим на одно и тоже число). Значит ответом будет вариант 3), т.к. там все время умножаем на (-3).

Вспоминаем, что убывающая геометрическая прогрессия - это последовательность чисел, которые постоянно уменьшаются во сколько-то раз. Значит ответом будет вариант 3) 16, 8, 4.

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.