Сборник практических задач" Мир практических задач"

Государственное общеобразовательное учреждение

Луганской Народной Республики

«Брянковская специализированная школа  № 23»

 

 

 

 

 

 

 

 

           

            

 

 

Предисловие

 

Пособие предназначено для школьников 5-х – 9-х классов,   учителей математики и для тех, кому интересна данная тема. Пособие поможет выпускникам  школы при подготовке к экзаменам.

     Данное пособие содержит основные способы решения задач на проценты, на движение, на смеси и сплавы, жизненные задачи, часто встречающиеся в различных жизненных ситуациях, и их решение, небольшую историческую справку,  интересные факты. В каждом разделе предлагаются  задачи для самостоятельного решения, в конце пособия имеются ответы.

 

 

 

 

Авторы:

(учащиеся 8 класса)

Шеститко Е., Чулакчи Э., Егурнов А., Парыгина В., Мироновская П., Урманов А., Морозова А., Боркунова А., Крецу А., Иванюк В., Печенежская Т., Бирюкова А., Осауленко Е., Печенежская Т., Карпова В., Булгакова М., Нежданов Ю., Серый Д.

 

 

Учитель-консультант: Скорикова Мария Андреевна, учитель математики.

 

 

 

Год издания -2018

 

 

 

 

 

 

 

Содержание

1.Введение.................................................................................................. 4

2.Памятка «Как работать над задачей»...................................................... 5

3.История возникновения процентов .......................................................  6

4.Основные способы решения задач на проценты .............................   7-21

4.1.Задачи на нахождения  процента от числа и число по его проценту.......... 7-11

4.2. Задачи на концентрацию, смеси и сплавы................................... 12-15

4.3 Задачи на процентное содержание компонентов  в различных  веществах 16-18

4.4 Задачи на проценты в ЖКХ и на различные виды услуг............... 19-21

5.Задачи на движение.......................................................................... 22-35

5.1. Задачи на движение в одном направлении и вдогонку................. 23-26

5.2. Задачи на встречное движение_................................................... 27-29

5.3. Задачи на противоположное движение......................................... 30-32

5.4. Задачи на движение по реке.......................................................... 33-35

6. Жизненные задачи........................................................................... 36-40

7. Задачи из сборника  заданий ГИА................................................... 41-47

8. Задачи от Григория Остера.............................................................. 48-51

9. Авторские задачи............................................................................. 52-53

10.Ответы к задачам............................................................................ 54-55

 

 

 

 

Введение

Проблема реализации практической направленности задач в процессе обучения математике школьников неоднократно рассматривалась в различных научных исследованиях. Теоретическое обоснование она получила в работах В.А. Гусева, Ю.М. Колягина, Г.Л. Луканкина, В.Л. Матросова, И.М. Смирновой и др.

 

В повседневной жизни люди постоянно сталкиваются с решением тех или иных ситуаций. Зачастую  приходится прилагать много усилий для разрешения возникших трудностей реальной жизни: люди  не знают с чего начать, как действовать, какое решение лучше предпринять. Для того чтобы в реальной жизни каждый человек мог не бояться встретившихся на его пути проблем, необходимо в школьном курсе разбирать такие задачи, которые будут отражать реальную действительность и которые можно с легкостью решить математическими методами.

Практические задачи являются средством и условием формирования способностей детей применять полученные на уроках по математике знания в  повседневной жизни.

 

Задачи практического содержания – это наша повседневная жизнь, наши профессии, успешная сдача учащимися ГИА и ЕГЭ.

 

Разбор задач практического содержания на уроках помогает повысить практическую значимость изучения математики в школе; научить необходимым навыкам решения таких задач и умениям рассчитывать величины и их примерное значение; усилить интерес, мотивацию к обучению математике; увеличить результативность обучения школьного курса математики.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Памятка работы над задачей

 

1.Прочитай задачу 3 раза, представь себе о то, о чем в ней говориться.

2.Докажи, что это задача (выдели условие и вопрос задачи карандашом).

3.Определи, какая задача по составу (простая или сложная).

4.Запиши задачу кратко или выполни чертеж.

5.Если задача составная, определи, что нужно узнать сначала, а что - потом.

6.Составь план решения задачи.

7.Запиши и прочти решение задачи. Проверь его.

8.Запиши и прочти вопрос на ответ задачи.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

История возникновения процентов.

 

Процент - имеет латинское происхождение: «pro centum» - это «на сто».  Процентом называется сотая часть числа. Проценты были известны в Индии ещё в V в. С давних пор счет велся в десятичной системе счисления. Также проценты были распространены в Древнем Риме. Римляне называли процентами деньги, которые платил должник заимодавцу за каждую сотню. Они  брали с должника лихву (т. е. деньги сверх того, что дали в долг).От римлян проценты перешли к другим народам в Европе. В средние века в Европе в связи с развитием торговли особо обращали внимание на умение вычислять проценты. Впервые опубликовал таблицы для расчета процентов Симон Стевин – инженер из города Брюгге (Нидерланды). Это произошло в 1584 году. Употребление термина «процент» в России начинается в конце XVIII в. Долгое время под процентами понималось исключительно прибыль или убыток на каждые 100 рублей. Проценты применялись только в торговых и денежных сделках.  В Италии слово cento (сто), писалось сокращенно cto. Путем дальнейшего упрощения из буквы t в наклонную черту произошел современный символ для обозначения процента - /.Есть  другая версия возникновения знака «%». Предполагается, что знак произошёл в результате опечатки, которую совершил наборщик. В 1685 году в Париже была опубликована книга «Руководство по коммерческой арифметике», где по ошибке наборщик вместо cto напечатал %.

 

 

 

 

 

 

 

 

Задачи на проценты

(основные способы решения)

 

Чтобы найти процент от числа, нужно:

1.Перевести проценты в  десятичную дробь .

2 Данное  число умножить на полученную дробь .

 

Задача 1. В классе 28 учеников .75%из них занимаются спортом .Сколько учеников в классе занимаются спортом?

 

Решение : Так как 75 % =0,75 ,то умножая число 28 на дробь 0,75 получаем : 0,75*28 =21

Ответ :21 человек занимается спортом .

 

Задача 2.Вода составляет 76% картофеля. Сколько килограммов воды в 35 кг картофеля?    

 Решение. Вода составляет 76% от 35 кг. По правилу нахождения процентов от данного числа (чтобы найти проценты от данного числа нужно обратить проценты в десятичную или обыкновенную дробь, а затем умножить данное число на эту дробь) получаем 0,76∙35=26,6 кг.

 Ответ: в 35 кг картофеля содержится 26,6 кг воды.

 Задача 3.В классе 20 человек. Контрольную работу по математике 25% учащихся написали на «5», 35 % написали на «4», 10% всех учащихся получили «2». Сколько пятерок, четверок, троек и двоек получил класс?

 

Решение. Количество пятерок составляет 25% от 20. По правилу нахождения процентов от данного числа это 0,25∙20=5 учащихся. Четверки получили 35% от 20. Это 0,35∙20=7 учащихся. Двоек 10%. Это 1/10 часть от 20 учащихся, т.е. 2 человека. Остальные учащиеся получили оценку «3». Их 20-5-7-2=6 человек.

Ответ: оценку «5» получило 5 учащихся; оценку «4» получили 7 учащихся; оценку «3» получило 6 учащихся и оценку «2» получили 2 ученика.

Чтобы найти число по его процентам, нужно:

1.     Перевести проценты в  десятичную дробь .

2.     Известное число в задаче разделить на  эту дробь

Задача 1.В школе на родительском собрании отсутствовало 12 человек, что составляет 7,5% от общего числа родителей .Сколько всего родителей должно было присутствовать на собрании ?

                                                    

Решение : Заменим 7,5 % десятичной дробью .Это будет 0,075 . Значит 12 человек ,отсутствовавших на собрании , составляют 0,075 от общего числа родителей .Таким образом ,в этой задаче нужно 12: 0,075 =160 .

Ответ :на родительском собрании было 160 родителей .

Задача 2. В школьной библиотеке 5780 учебников, что составляет 85% всех книг, имеющихся в библиотеке. Сколько всего книг в школьной библиотеке?

 

 Решение. Потребуется найти число по его процентам. Применяем правило нахождения числа по его процентам (чтобы найти число по его процентам нужно обратить проценты в десятичную дробь, а затем разделить данное число на эту дробь). 1) 85%=0,85; 2) 5780:0,85=578000:85=6800 книг.

 Ответ: всего в библиотеке 6800 книг.

Задача 3.Фирма платит рекламным агентам 5% от стоимости заказа. На какую сумму нужно выполнить заказ, чтобы заработать 2000 рублей?

 Решение. 2000 рублей – это 5% от заказа. Число (все его 100%) по его процентам мы найдем по правилу нахождения числа по его процентам. Обращаем 5% в десятичную дробь и делим 2000 на эту дробь. 1) 5%=0,05; 2) 2000:0,05=200000:5=40000.

 Ответ: заказ должен быть на сумму 40000 рублей.

Чтобы найти процентное отношение двух чисел ,нужно:

   1. Найти отношение данных чисел.

2.Результат умножить на 100.

 

Задача 1.Завод должен был за месяц изготовить 1200 изделий , а изготовил 2300 изделий. На сколько процентов завод перевыполнил план ?

 

Решение : 1200 изделий –это план завода ,или 100% плана . 2300-1200=1100изделий-на столько изделий завод перевыполнил план . Найдём  1100 от 1200. 1100 :1200 * 100 = 91 ,7%.

Ответ: 91 ,7%.

Задача 2. За 1 час станок-автомат изготовлял 240 деталей. После реконструкции этого станка он стал изготовлять в час 288 таких же деталей. На сколько процентов повысилась производительность станка?       

 

 Решение. Производительность станка повысилась на 288-240=48 деталей в час. Нужно узнать, сколько процентов от 240 деталей составляют 48 деталей. Для того чтобы узнать, сколько процентов число 48 составляет от числа 240 нужно число 48 разделить на 240 и результат умножить на 100%.

 Ответ: производительность станка повысилась на 20%.

 

 

 

 

 

 

Задачи для самостоятельного решения

Задача 1.Зонт стоил 360 рублей. В ноябре цена зонта была снижена на 15%, а в декабре еще на 10%. Какой стала стоимость зонта в декабре?

Задача 2.Шариковая ручка стоит 40 рублей. Какое наибольшее число таких ручек можно будет купить на 900 рублей после повышения цены на 10%?

Задача 3.Банк выплачивает вкладчикам каждый месяц 2% от внесённой суммы. Клиент сделал вклад в размере 500 рублей. Какая сумма будет на его счёте через полгода?                                                                                                                  

 

Задача 4. В школе 400 учащихся, 52% этого числа составляют девочки. Сколько мальчиков в школе?

 

 

Задача 5.Цена на электрический чайник была повышена на 16% и составила 3480 рублей. Сколько рублей стоил чайник до повышения цены?

 

 

Задача 6.За зиму медведь Вини Пух съел 16 горшочков меда. Сколько горшочков меда заготовил Вини Пух, если у него осталось 20% всех его запасов?

 

 

Задача 7.У Лены в аквариуме 8 меченосцев, что составляет 40% всех ее рыбок. Сколько всего рыбок у Лены в аквариуме?

Задача 8.Из 25 килограммов  свежих яблок получили 4 килограмма сушёных. Насколько процентов уменьшилась масса яблок при сушке?

 

 

Задача 9.Футболка стоила 1200 рублей. После снижения цены она стала стоить 972 рубля. На сколько процентов была снижена цена на футболку? 

 

 

 

Задача 10. Для приготовления компота купили 2 кг чернослива, 1кг изюма, 4 кг кураги, 5 кг сушёных яблок, 3 кг сушёных груш. Сколько процентов всего компота составляют груши?

 

 

 

 

 

 

 

 

 

 

 

Задачи на концентрацию, смеси и сплавы.

(основные способы решения)

     Задача 1. Сколько килограммов соли в 10     

килограммах соленой воды, если процентное 

содержание соли составляет 15%?

 

Решение:10 · 0,15 = 1,5 (кг) соли.                                            

 Ответ: 1,5 кг.

 

Задача  2. Сплав содержит 10 кг олова и   15 кг  цинка.  Каково процентное содержание олова и цинка в сплаве?

 

Решение: Процентное содержание вещества в сплаве – это часть, которую составляет  вес данного вещества от веса всего сплава.

1) 10 + 15 = 25 (кг) – сплав;

2) 10:25 · 100% = 40% – процентное содержание олова в сплаве;

3) 15:25 · 100% = 60% – процентное содержание цинка в сплаве.

 Ответ: 40%, 60%.

  Задача  3. Имеются два слитка сплава золота с медью. Первый слиток содержит 230 г золота и 20 г меди, а второй слиток – 240 г золота и 60 г меди. От каждого слитка взяли по куску, сплавили их и получили 300 г сплава, в котором оказалось 84 % золота. Определить массу (в граммах) куска, взятого от первого слитка.

 

Решение: Определим процентное содержание золота в обоих слитках.

1) 230+20=250(г) - масса 1 слитка,

2) 230:250=0,92 (92%) - процентное содержание золота в 1 слитке.

3) 240+60=300(г) - масса 2 слитка,

4) 240:300=0,8 (80%)- процентное содержание золота во 2 слитке.

Пусть х масса куска, взятого от 1 слитка, (300-х)- масса куска, взятого от 2 слитка, получим уравнение:

                                 0,92х+0,8(300-х)=0,84·300

                                  0,92х+240-0,8х=252

                                  0,12х=12

                                  х=10

  Ответ: 100 г.

Задача 4.Смешали некоторое количество 15-процентного раствора некоторого вещества с таким же количеством 19- процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора? 

Решение:

  Пусть масса первого раствора х г, он содержит 0,15х г чистого вещества. Масса второго раствора тоже х г, он содержит 0,19х г чистого вещества. Масса нового раствора равна х + х = 2х г и он содержит 0,15х + 0,19х = 0,34х г чистого вещества. Тогда концентрация нового раствора равна ( 0,34х): (2х)×100% = 17%.

Ответ: 17.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Задачи для самостоятельного решения

Задача 1.Садовник для поливки роз смешивает удобрение «Росток» с 30%-ым содержанием калия и удобрение «Розочка» с 10%-ым содержанием калия и получает  600 граммов  15%-ого раствора. Сколько граммов  каждого удобрения было взято?

 

 

Задача 2.Смешали 4 литра 15%-ого водного раствора некоторого вещества с 6 литрами  25%-ого водного раствора того же вещества. Ск олько процентов составляет концентрация полученного раствора?

 

 

Задача 3.Смешав 30%-ый  и 60%-ый растворы кислоты и,  добавив 10 кг чистой воды, получили 36%-ый  раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50%-ого  раствора той же кислоты, то получили бы 41%-ый  раствор кислоты. Сколько килограммов 30%-ого  раствора использовали для получения смеси?

 

 

Задача 4.Первый сплав содержит 10% меди, второй – 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

 

Задача 5.Имеется два сплава. Первый сплав содержит 10% никеля, второй – 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?

 

Задача 6.Хозяйке для засолки огурцов необходимо получить 6%-ый раствор уксусной кислоты, используя 70%-ый раствор уксусной кислоты и воду. Сколько необходимо взять 70%-ого раствора и воды, чтобы получить 700 г раствора необходимой концентрации? 

 

 

Задача 7.Сколько граммов воды надо добавить к 50 г раствора, содержащего 8 % соли, чтобы получить 5 % - ный раствор? 

 

 

Задача 8.Имеются два сплава. Первый сплав содержит 10% никеля, второй 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25 % никеля. Насколько кг масса первого сплава меньше массы второго?

 

 

 

 

 

Задача 9. Смешали 4 литра 15-процентного раствора некоторого вещества с 6 литрами 25-процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

 

 

 Задача 10.В сосуд, содержащий 5 литров 12-процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?

 

 

 

 

 

 

 

 

 

 

 

Задачи на процентное содержание компонентов  в различных  веществах.

(основные способы решения)

 

Задача 1. Виноград содержит 90%  влаги, а изюм — 5%.

Сколько килограммов винограда требуется для получения 20 килограммов изюма?

 

Внимание! Если вам встретилась задача «о продуктах», то есть такая, где из винограда получается изюм, из абрикосов урюк, из хлеба сухари или из молока творог — знайте, что на самом деле это задача на растворы. Виноград мы тоже можем условно изобразить как раствор. В нем есть вода и «сухое вещество». У «сухого вещества» сложный химический состав, а по его вкусу, цвету и запаху мы могли бы понять, что это именно виноград, а не картошка. Изюм получается, когда из винограда испаряется вода. При этом количество «сухого вещества» остается постоянным. В винограде содержалось 90%  воды, значит, «сухого вещества» было 10%. В изюме 5%  воды и 95%  «сухого вещества». Пусть из х кг винограда получилось 20 кг изюма. Тогда 10%  от х равно 95%  от 20

Составим уравнение:

        0,1х=0,95·20
0,1х=19

        х=19:0,1

        х=190

Ответ: 190 кг.

 

    Задача  2. Свежие грибы содержали по массе 90% воды, а сухие 12%. Сколько получится сухих грибов из 22 кг свежих?

             

Решение: 1) 22 · 0,1 = 2,2 (кг) - грибов по массе в свежих грибах;

     2) 2,2 : 0,88 = 2,5 (кг) - сухих грибов, получаемых из свежих.                                     

    Ответ: 2,5 кг.

 

Задача 3. Сколько килограммов  белых грибов надо собрать для получения 1 килограмма  сушеных, если при обработке свежих грибов остается 50% их массы, а при сушке остается 10% массы обработанных  грибов?

Решение: 1 кг сушеных грибов – это 10% или 0, 01 часть обработанных, т.е. 1 кг : 0,1=10 кг обработанных грибов, что составляет 50% или 0,5 собранных грибов, т.е.

10 кг : 0,05 = 20  Ответ: 20 кг.

     Задача  4. Свежие груши содержали 72% воды, а сухие - 20%. Сколько сухих фруктов получится из 20 кг свежих груш?

Решение: В свежих грушах сухой остаток составляет 100% - 72% = 28%. В 20 кг свежих груш сухой остаток составляет 20·0,28 = 5,6 (кг). В сухих грушах сухой остаток составляет 100% - 20% = 80%. 5,6 кг сухого остатка будет в 5,6:0,8 = 7 кг сухих фруктов.

           Ответ: 7 кг.

 

     Задача 5. Хранили 20 кг крыжовника, ягоды которого содержат 99% воды. Содержание воды в ягодах уменьшилось до 98%. Сколько крыжовника получилось в результате?

Решение: На первый взгляд, кажется, что вес ягод мало изменился, но это только на первый взгляд! Вес сухого «вещества» в ягодах составлял 100-99=1(%), или 20·0,01=0,2(кг). После сушки его вес составляет 100-98=2(%) от нового веса ягод. Найдём новый вес ягод: 0,2:0,02=10(кг).

  Ответ: после сушки вес ягод уменьшился в два раза.

    

 

 

 

 

 

Задачи для самостоятельного решения

 Задача 1.Из 25 килограммов  свежих яблок получили 4 килограмма сушёных. На сколько процентов уменьшилась масса яблок при сушке?

 

 

Задача  2.Фасоль содержит 23% белка, 55% крахмала и 1,8% жиров. Сколько килограммов белка, крахмала и жиров содержится в 15 килограммах фасоли?

 

  Задача  3.Влажность свежих грибов  99%, сушеных – 98%. Как изменился вес грибов после подсушивания?

 

 

 

 Задача 4.Из молока получается 10% творога. Сколько творога получают из 40 кг молока?

 

 

 

 

 

  Задача 5. Арбуз массой 20 кг содержал 99% воды. Когда он немного усох, содержание воды в нем уменьшилось до 98%.  Какова теперь масса арбуза?

 

 

 Задачи на проценты в ЖКХ и на различные виды услуг.

(основные способы решения)

  Задача 1. В газете сообщается, что с 1 октября согласно новым тарифам стоимость 1 кубического метра газа составит 3 рубля вместо 2 рублей 81 копейки. На сколько процентов выросла цена на газ?

Решение: Разность тарифов составляет 0,19 руб., а ее отношение к старому тарифу примерно равно 0,068.  Выразив это отношение в процентах, получим примерно 6,8 %.

Ответ: на 6,8%.

 

Задача 2. В газете сообщается, что с 10 июня согласно новым тарифам стоимость отправления почтовой открытки составит 3 рубля 15 копеек вместо 2 рублей  27 копеек. Соответствует ли рост цен на услуги почтовой связи росту цен на товары в этом году, который составляет 14,5%?

Решение: Разность тарифов составляет 0,4 рубля, а ее отношение к старому тарифу примерно  равно 0,145. Выразив это отношение в процентах, получим примерно 14,5%.

 

Дополнительный вопрос. Сколько будет стоить отправка заказного письма, если эта услуга сейчас оценивается в 5 рублей 50 копеек?

Решение: Цена услуги увеличивается на 14,5%, т.е. станет 5,5·1,145 ≈ 6,3 рубля.

Ответ: да, соответствует; 6,3 рубля.

 

Задача 3. Занятия ребенка в музыкальной школе родители оплачивают в сбербанке, внося ежемесячно 250 рублей. Оплата должна производиться до 15 числа каждого месяца, после чего за каждый просроченный день начисляется пеня в размере 4% от суммы оплаты занятий за один месяц. Сколько придется заплатить родителям, если они просрочат оплату на неделю?

Решение: Так как 4% от 250 рублей составляют 10 рублей, то за каждый просроченный день сумма оплаты на день  им придется заплатить 250+10 = 260 рублей, на неделю

250+ 10 ·7 = 320 рублей.

Ответ: 320 рублей.

Задача 4. Стоимость проезда в городском автобусе составляла 1 рубль 60 копеек. В связи с инфляцией она возросла на 150%. Во сколько раз возросла стоимость проезда в автобусе?

Решение: 1) 1,60+1,60 ·1,5= 4(руб.) – стоимость проезда после повышения на 150%;

2) 4 : 1,6 = 2,5.

Ответ: в 2,5 раза.

 

Задача 5. У Миши на счете сотового телефона было 10 рублей. Он заплатил за пользование телефоном 120 рублей. Оплачивал он в банкомате, комиссия в котором составляет 5%. Сколько денег оказалось на телефоне у Миши?

Решение: Примем 120 руб. за 100%. Определим комиссию 5% от 120 руб.

120 руб. – 100%

х руб. – 5%

х= 120·5:100 = 6(руб.)

На счет телефона поступит 120 – 6 = 114 руб.

Так как у Миши было 10 руб., то всего на счете будет

114+10 = 124 руб.

Ответ: на счете будет 124 рубля.

 

 

 

 

 

 

 

 

Задачи для самостоятельного решения

Задача 1.В начале года тариф на электроэнер­гию составлял 40 копеек за 1 кВт·ч. В  середине года он увеличился на 50%, а в конце года - еще на 50%. Каков стал тариф в конце года?

 

 

Задача 2.Стоимость проезда в городском авто­бусе составляла 5 рублей. В связи с инфляцией она  воз­росла на 200%. Во сколько раз повысилась стои­мость  проезда в автобусе?

 

 

 

Задача 3.Ежемесячная плата за квартиру увеличится на 6% и семье придётся платить 1484 рубля. На сколько рублей увеличится плата за квартиру?

 

 

Задача 4.В декабре цены на жильё упали на 4%, а в марте выросли на 6%.  На сколько рублей   увеличилась стоимость 1 квадратного метра  жилья, если его первоначальная стоимость 60000 рублей?

 

Задача 5.Первоначальная стоимость коммунальных услуг была 200 рублей, через год она увеличилась на 30%, а еще через  полгода  еще  на  20%.  Сколько  стоят  новые  коммунальные услуги?

 

 

 

 

 

 

 

Задачи на движение в математике

 

Задачи на движение имеют важное практическое значение: это единственный вид учебных задач, в процессе решения которых  необходимо использовать сразу несколько различных информационных и математических моделей: графические (чертеж, схема, граф), реляционные (таблица) и алгебраические (алгебраические выражения, уравнения, неравенства, системы уравнений и неравенств). Графическая модель позволяет лучше понять взаимосвязи и отношения, описанные в условии задачи, табличная модель – определить наиболее удобный способ решения, математическая модель строится с целью получения ответа на поставленный вопрос. Таким образом, задачи на движение могут с успехом использоваться, в том числе, и при обучении моделированию.

Одной из особенностей задач на движение является то, что всякая такая задача требует обязательного анализа. Без предварительного анализа трудно определить, какой метод, и какая соответствующая математическая модель являются наиболее подходящими для решения данной задачи. Процессы реальной жизни характеризуются величинами, между которыми существуют определенные зависимости.

 

 

 

 

 

Задачи на движение

Задачи на движение в одном направлении и вдогонку

(основные способы решения)

 

Задача 1  Бабочка - капустница пролетела 47  со скоростью 4 м/с, а когда подул попутный ветер, скорость бабочки увеличилась на 6 м/с, и она пролетела ещё некоторое количество метров. Какое расстояние бабочка пролетела при попутном ветре, если всего она пролетела 688 м?

Решение:

1.   47-4=188 (м) пролетела бабочка 47 с.

2.   4+6 =10 (м/с) скорость бабочки при попутном ветре.

3.   688-188=500 (м) пролетела при попутном ветре.
Ответ: 500 метров.

 

 Задача 2. Велосипедист проехал 64 км со скоростью 16 км/ч и еще 51 км со скоростью 17 км/ч. Какое время он затратил на всю дорогу?

Решение:

1.    64:16=4(ч) -время первого пути.

2.    51:17=3(ч) - время второго пути.

3.    4+3=7(ч) - затратил на всю дорогу.

Ответ: 7часов.

 

Задача 3.Автомобилист проехал за два дня 770км. В первый день он ехал 4ч со скоростью 80км/ч, во второй день он ехал со скоростью 90км/ч. Сколько часов был в пути автомобилист во второй день?

Решение:

         1)80*4=320(км)-1день.

         2)770-320-450(км) - разница

          3)450:90=5(ч).

Ответ: 5часов.

 

 

Задача 4.Расстояние между двумя станциями 40 км. Из этих станций одновременно в одном направлении вышли скорый и товарный поезда, причем товарный поезд едет впереди. Через сколько часов скорый поезд догонит товарный, если его скорость равна 80 км/ч, а скорость товарного поезда — 60 км/ч?

 

Решение:

1) 80-60=20 (км/ч) скорость сближения поездов

2) 40:20=2 (ч) через такое время скорый поезд догонит товарный.

Ответ: через 2 ч.

 

Задача 3.Расстояние между пунктами равно 50 км. Из этих пунктов одновременно в одном направлении выезжают велосипедист и мотоциклист, причем велосипедист едет впереди. Скорость велосипедиста равна 13 км/ч, скорость мотоциклиста — 38 км/ч. На каком расстоянии от пункта своего выезда мотоциклист догонит велосипедиста?

Решение:

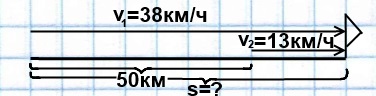
1) 38-13=25 (км/ч) скорость сближения мотоциклиста и велосипедиста

2) 50:25=2 (ч) через столько часов после своего выезда мотоциклист догонит велосипедиста

3) 38∙2=76 (км) на таком расстоянии от пункта своего выезда мотоциклист догонит велосипедиста.

Ответ: 76 км.

 

 

 

 

 

Задачи для самостоятельного решения

 

Задача 1. Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?

Задача 2. Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?

 

Задача 3.Санки съехали с горки за 10сек., со скоростью 2м/сек, а потом по ровной дороге проделали путь в два раза больший. Сколько всего метров проехали санки?

 

Задача 4.Часть пути до школы школьник шёл со скоростью 50 м/мин в течение 4мин. Остальную часть пути он шёл со скоростью 80м/мин. На весь путь до школы он затратил 10мин. Чему равно расстояние до школы?

 

 

Задача 5. От дома до леса лыжник шёл 2ч со скоростью 8км/ч. По лесу он шёл со скоростью 7км/ч. Сколько времени он шёл по лесу, если всего прошёл 37км?

 

 

 

Задача 6. Пассажирский поезд отправился во Владивосток. Когда от станции отправления он отошёл на расстояние 342 км, от того же вокзала в том же направлении вышел скорый поезд. С какой скоростью шёл скорый поезд, если скорость пассажирского 50 км/ч, и скорый догнал его через 9 часов?

 

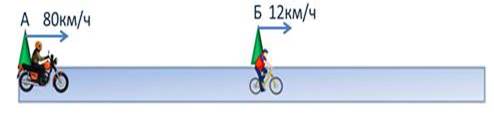Задача 7. Из города А выехал мотоциклист, а из города Б одновременно с ним выехал велосипедист. Скорость мотоциклиста 80 км/ч, а скорость велосипедиста – 12 км/ч. Через 3 ч мотоциклист догнал велосипедиста. На каком расстоянии друг от друга находятся города А и Б?

 

 

 

 

 

 

 

 

 

 

Задачи на встречное движение

(основные способы решения)

 

Задача 1.Из двух городов одновременно навстречу друг другу вышли 2 поезда. Скорость первого 90 км/ч, и он проехал до встречи 360 км. Второй поезд проехал до встречи 280 км. Какова его скорость?

Решение:

1) 360:90=4(ч)-время движения поезда.

2) 280:4=70(км/ч)-скорость второго поезда.

Ответ: 70 км/ч.

 

Задача 2.Ехали две машины на встречу друг к другу одна из Ангарска другая из Байкальска. Скорость первой машины 35км/ч, а другой 32км/ч. Найдите расстояние между Ангарском и Байкальском если они встретились через два часа?

Решение:

1) 35-2-70(км/ч)- первая машина доедет до места встречи за два часа.

2)32∙2-64(км/ч)- вторая машина доедет до места встречи за два часа.

 3) 70+64=434(км) -расстояние между Ангарском и Байкальском.

Ответ: расстояние равно 134км.

 

Задача 3.Две машины едут навстречу друг другу. Первая едет со скоростью 115 км/ч. скорость другой на 25 км/ч меньше скорости первой. Расстояние между городами 615 км. Через сколько часов машины встретятся?

Решение:

               1)115- 25 - 90 (км/ч)- скорость первой машины.

2)115 +90 = 205(км/ч) - скорость сближения.

3)615 : 205 = 3 (ч)- время через которое машины встретятся.

Ответ: 3 часа.

 

 

 

 

 

Задачи для самостоятельного решения

Задача 1.Расстояние между городами А и В 720 км. Из А в В вышел скорый поезд со скоростью 80 км/ч. Через 2 часа навстречу ему из В в А вышел пассажирский поезд со скоростью 60 км/ч. Через какое время они встретятся?

 

Задача 2. Винни-Пух собирается пойти навстречу своему другу Пятачку, который тоже собирается идти к нему в гости. Расстояние между их домами 840 метров. Винни- Пух идет со скоростью 42 м/мин, а Пятачок – 63 м/мин. а) Через сколько минут они встретятся, если выйдут одновременно? б) Через сколько минут после выхода из дома Винни-Пух встретит Пятачка, если Винни -Пух выйдет на 5 минут раньше него? в) На сколько минут раньше нужно выйти Винни-Пуху из своего дома, чтобы застать Пятачка дома?

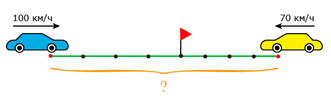
Задача 3. Два автомобиля выехали одновременно из двух населённых пунктов и встретились через 4 часа. Первый автомобиль ехал со скоростью 100 км/ч, а второй – со скоростью 70 км/ч. На каком расстоянии друг от друга находятся населённые пункты?

 

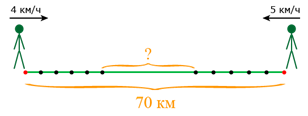
Задача 4.Из двух посёлков навстречу друг другу вышли одновременно два пешехода. Скорость первого пешехода 4 км/ч, а скорость второго пешехода 5 км/ч. Какое расстояние будет между пешеходами через 5 часов после выхода, если расстояние между посёлками 70 км?

 

 

Задача 5. Два мальчика одновременно побежали навстречу друг другу по спортивной дорожке, длина которой 200 м. Они встретились через 20 с. Первый бежал со скоростью 5 м/сек. С какой скоростью бежал второй мальчик?

 

Задача 6. От двух пристаней отошли одновременно навстречу друг другу катер и лодка и встретились чере 3 ч. Скорость лодки - 15 км/час, скорость катера - в 4 раза больше. Найдите расстояние между пристанями.

 

 

Задача 7. Из двух деревень одновременно навстречу друг другу вышли девочка, которая двигалась со скоростью 3 км/час, и мальчик, который двигался в 2 раза быстрее, чем девочка. Встреча произошла через 4 часа. Какое расстояние между деревнями?

 

 

Задача 8.Расстояние между сёлами 48 км. Через сколько часов встретятся два пешехода, которые вышли одновременно навстречу друг другу, если скорость одного - 3 км/час, а другого - 5 км/час?

 

 

 

 

 

 

Задачи на противоположное движение

(основные способы решения)

 

 Задача 1.Из одного поселка одновременно в противоположных направлениях выехали велосипедист и мотоциклист. Скорость велосипедиста 13 км/ч, скорость мотоциклиста - в 5 раз больше. Через какое время расстояние между ними будет 156 км?

Решение:

      1)13∙5=65(км/ч) - скорость мотоцикла.

 2)65-13=52(км/ч)- скорость удаления.

 3)156:52=через3(ч)- расстояние между мотоциклом и велосипедом будет 156 км.

Ответ: 3 часа.

 

Задача 2.Из пункта А выехали две машины в противоположном направлении. Скорость первой машины 6Окм/ч, а другой 40км/ч. На каком расстоянии Они будут через два часа друг от друга?

Решение:

      1) 60∙2=120(км)- расстояние, пройденное первой машиной.

      2)40∙2=80(км) - расстояние, пройденное второй машиной.

      3) 12О+80=200(км)- расстояние, которое они будут через два часа друг от друга.

Ответ: 200км расстояние, которое они будут через два часа друг от друга.

 

Задача 3.От гнезда одновременно в противоположных направлениях полетели 2 ласточки. Скорость первой 18 м/с, второй - на 2 м/с меньше. Через какое время расстояние между ними будет 680 м?

Решение:

   1)18-2=16 (м/с)- скорость второй ласточки.

   2)18 + 16=34(м/с)- скорость удаления.

  3) 680:34=20 (с) - преодолеют расстояние 680 километров
Ответ: 20 секунд

 

 

 

 

Задачи для самостоятельного решения

Задача 1.Два самолета вылетели одновременно с аэродрома в противоположных направлениях. Через 20мин после вылета расстояние между ними было 540км. Первый летел со скоростью 900км/ч. С какой скоростью летел второй самолет?

Задача 2. Два автомобиля выехали одновременно из одного и того же пункта в противоположных направлениях. Скорость первого автомобиля 100 км/ч, скорость второго – 70 км/ч. Какое расстояние будет между автомобилями через 4 часа?

Задача 3. Из двух населённых пунктов, расстояние между которыми 40 км, вышли в противоположных направлениях два пешехода. Первый пешеход шёл со скоростью 4 км/ч, а второй - 5 км/ч. Какое расстояние между пешеходами будет через 5 часов?

 

Задача 4.Из одного города одновременно в противоположных направлениях выехали автобус и мотоцикл. Скорость автобуса 40 км/ч, мотоцикла — в 2 раза больше. Какое расстояние будет между ними через 3 ч?

Задача 5. Из одного посёлка вышли в одно и то же время в противоположных направлениях два пешехода. Скорость одного 5 км/ч, скорость другого — 6 км/ч. Через сколько часов расстояние между ними будет равно 33 км?

 

 

 

Задача 6. Машина и автобус выехали с автостанции одновременно в противоположных направлениях. Скорость автобуса в два раза меньше скорости автомобиля. Через сколько часов расстояние между ними будет 450 км, если скорость автомобиля 60 км/час?

 

 

Задача 7.Из города на дачу выехал велосипедист со скоростью 12 км/час. Дорога на дачу заняла 6 часов. На сколько изменилась скорость велосипедиста на обратном пути, если он затратил на него 4 часа?

Задача 8. Грузовой и легковой автомобили отправились от автостанции в разных направлениях. За одно и тоже время грузовик проехал 70 км, а легковой автомобиль 140 км. С какой скоростью двигался легковой автомобиль, если скорость грузовика 35 км/час?

 

Задача 9.Два крестьянина вышли из одного поселка одновременно в противоположных направлениях. Один двигался со скоростью 3 км/час другой 6 км/час. Какое расстояние будет между крестьянами через 5 часов.

 

Задача 10.Такси двигалось со скоростью 60 км/час, автобус в 2 раза медленнее. Через сколько времени между ними будет 360 км, если они движутся в разных направлениях?

 

 

 

 

Задачи на движение по реке

(основные способы решения)

Правило.

Если судно плывет по течению реки, то к собственной скорости судна нужно прибавить скорость течения реки.

Если судно плывет против течения реки, то из собственной скорости судна нужно вычесть скорость течения реки.

 

Задача 1. Катер движется против течения реки. За сколько часов он преодолеет расстояние 112 км, если его собственная скорость 30 км/ч, а скорость течения реки 2 км/ч?

Решение: Сначала узнаем скорость движения катера против течения реки, для этого от его собственной скорости отнимем скорость течения:

30 - 2 = 28 (км/ч) – скорость движения катера против течения.

Теперь можно узнать за сколько часов катер преодолеет 112 км, разделив расстояние на скорость:

112 : 28 = 4 (ч)

Решение задачи по действиям можно записать так:

1) 30 - 2 = 28 (км/ч) – скорость движения катера против течения

2) 112 : 28 = 4 (ч)

Ответ: За 4 часа катер преодолеет расстояние 112 км.

 

 

 

 

 

Задача 2. Расстояние от пункта A до пункта B по реке равно 120км. Сколько времени потратит моторная лодка на путь от пункта A до B, если её собственная скорость 27 км/ч, а скорость течения реки 3 км/ч?

Рассмотрите два варианта: 1) лодка движется по течению реки; 2) лодка движется против течения реки.

Решение: Если моторная лодка будет двигаться по течению реки, то её скорость будет равна сумме собственной скорости со скоростью течения реки:

27 + 3 = 30 (км/ч)

Значит расстояние между пунктами лодка преодолеет за:

120 : 30 = 4 (ч)

Если лодка будет двигаться против течения реки, то её скорость будет равна разности собственной скорости и скорости течения реки:

27 - 3 = 24 (км/ч)

Значит, чтобы узнать сколько времени потратит лодка на путь от пункта A до пункта B, надо расстояние разделить на скорость:

120 : 24 = 5 (ч)

Решение задачи по действиям для движения по течению реки можно записать так:

1) 27 + 3 = 30 (км/ч) – скорость лодки

2) 120 : 30 = 4 (ч)

Для движения против течения реки решение задачи по действиям можно записать так:

1) 27 - 3 = 24 (км/ч) – скорость лодки

2) 120 : 24 = 5 (ч)

Ответ:
1) При движении по течению реки моторная лодка потратит 4 часа на путь от пункта A до пункта B.
2) При движении против течения реки моторная лодка потратит 5 часов на путь от пункта A до пункта B.

Задачи для самостоятельного решения

 

Задача 1. Скорость катера 40 км/ч, а скорость течения реки 3 км/ч. С какой скоростью катер будет двигаться по течению реки? Против течения реки?

 

 

Задача 2. Скорость теплохода в стоячей воде — 23 км/ч. Скорость течения реки — 3 км/ч. Какой путь пройдет теплоход за 3 часа по течению реки? Против течения?

 

 Задача 3.Двигаясь по течению реки, за 6 часов лодка
прошла 102 км. Определите собственную скорость лодки,
если скорость течения – 4 км/ч.

 

Задача 4. За какое время при движении против течения реки лодка пройдет 56 км, если скорость течения – 2 км/ч, а её
собственная скорость на 8 км/ч больше скорости течения?

 

Задача 5. Двигаясь против течения реки, за 5 часов лодка
прошла 110 км. Определите собственную скорость лодки,
если скорость течения – 4 км/ч.

 

 

 

 

 

 

 

Жизненные задачи

Математика окружает нас везде. Благодаря ей мы решаем множество вопросов в повседневной жизни. С древних времен в своей повседневной жизни человек не мог обойтись без счета. У каждого народа необходимость в простейших арифметических подсчетах возникала задолго до появления первых зачатков письменности, потому что постижение Мира во всем его многообразии постоянно требовало количественной оценки обретенных знаний. Самой древней математической деятельностью был счет. Счет был нужен, чтобы следить за поголовьем скота и вести торговлю. Некоторые первобытные племена подсчитывали количество предметов, сопоставляя им различные части тела, главным образом пальцы рук и ног.

В основе развития математики лежат запросы практической деятельности человека. "Возникновение и развитие наук обусловлено производством", - писал Ф. Энгельс. - " Математика возникла из практических нужд людей: из измерения площадей земельных участков и вместимости сосудов, из счисления времени и из механики".

          

 

 

 

 

 

 

 

 

Жизненные задачи

Задача 1.Хозяйка квартиры решила покрасить стены чулана на высоту 1,5 м от пола. Какое количество краски (кг) нужно приобрести, если на 1 м² расходуется 300 граммов краски (дверь 0,8 м на 2 м не красится). Длина чулана 3 м, ширина 2 м, высота 2,5.

Решение:

         1)2· (2+3) · 1,5 = 2· 5· 1,5 = 15 (м²) – площадь боковой поверхности;

2)0,8 · 1,5 = 1,2 (м²) – площадь двери;

3)15       – 1,2 – 13,8 (м²) – площадь под покраску;

4)013,8 · 0,3 = 4,14 (кг) – масса краски;

Ответ: 4,14 кг

Задача 2.Стены и потолок ванной комнаты решили выложить кафельной плиткой.  Какое количество клея нужно приобрести, если на 1 м² расходуется 1,4 кг клея. Размеры комнаты: длина 3 м, ширина 2 м, высота 2,5 м. Дверь 0,8 м на 2 м.

Решение:

1)2*3 = 6 (м²) – площадь потолка;

2)2*· 0,8 = 1,6 (м²) – площадь двери;

3)3· 2 · 2,5 + 2 · 2,5 · 2  = 15 + 10 = 25 (м²) – площадь стен;

4)25+6 – 1,6 = 31 – 1,6 = 29,4 (м²) – площадь под покраску;

5)29,4 · 1,4 = 41,16 (кг) – масса клея.

Ответ: 41,16 (кг)

 

 

 

  Задача 3.  Курс воздушных ванн начинают с 15 минут в первый день и увеличивают время этой процедуры в каждый следующий день на 10 минут. Сколько дней следует принимать воздушные ванны в указанном режиме, чтобы достичь их максимальной продолжительности 1ч 45мин?

 

Решение:

 Ряд,  составленный из длительностей воздушных ванн, является арифметической прогрессией, так как каждое следующее число можно получить из предыдущего, прибавив к нему 10 минут. Значит:

d = 10

 a1 = 15 мин

 an = 1 ч 45 мин = 60 + 45 = 105 мин

 Таким образом, нам нужно найти номер n. Применим формулу вычисления n-ого члена арифметической прогрессии: an = a1 + d ⋅ (n - 1) 105 = 15 + 10 ⋅ (n – 1) 10n – 10 + 15 = 105 10n = 100 n = 10

Ответ: 10

Задача  4.Шоколадка стоит 30 рублей. В воскресенье в супермаркете действует специальное предложение: заплатив за две шоколадки, покупатель получает три (одну в подарок). Сколько шоколадок можно получить на 500 рублей в воскресенье?

Решение:

Найдем, сколько на 500 рублей можно купить всего шоколадок (без учета подарков). Для этого 500 рублей делим на стоимость 1 шоколадки:

500 : 30  = 16,6… Получаем дробное  число. Но мы понимаем, что дробное количество шоколадок купить нельзя, поэтому получившееся значение округляем до целого числа, причем в меньшую сторону. Получается, что на 500 рублей можно купить 16 шоколадок.

Теперь узнаем, сколько шоколадок можно получить в подарок. Мы знаем, что при покупке 2-х шоколадок 3-я в подарок, поэтому определим, сколько таких пар: 16 : 2 = 8 пар  шоколадок, при покупке которых идет одна шоколадка в подарок. Следовательно, в подарок пойдет 8 шоколадок.

Прибавим к 16 шоколадкам 8 шоколадок подарочных, тем самым найдем количество шоколадок, которое можно получить, потратив не более 500 рублей:16 + 8 = 24

Ответ: 24шоколадки

Задачи для самостоятельного решения

 

 Задача  1.  Отдыхающий, следуя совету врача, в первый день загорал 5 минут. А в каждый последующий день увеличивал время пребывания на солнце на 5 минут. НА какой день время пребывания на солнце будет равно 40 минут?

 

Задача  2. В соревновании по стрельбе за каждый промах в серии из 25 выстрелов стрелок получал штрафные очки: за первый промах - одно очко, за каждый последующий- на 0,5 очка больше, чем за предыдущий. Сколько раз попал в цель стрелок, получивший 7 штрафных очков?

 

 

 

Задача  3.  В угловом секторе стадиона в первом ряду 7 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько мест в 26-ом ряду?

 

Задача 4.Сырок стоит 8 рублей 40 копеек. Какое наибольшее число сырков можно купить на 70 рублей?

 

Задача 5.Стоимость проездного билета на месяц составляет 750 рублей, а стоимость билета на одну поездку — 19 рублей. Аня купила проездной и сделала за месяц 45 поездок. На сколько рублей больше она бы потратила, если бы покупала билеты на одну поездку?

Задача  6.Летом килограмм клубники стоит 90 рублей. Маша купила 1 кг 200 г клубники. Сколько рублей сдачи она должна была получить с 500 рублей?

 

Задача  7. В летнем лагере на каждого участника полагается 70 г сахара в день. В лагере 163 человека. Сколько килограммовых пачек сахара понадобится на весь лагерь на 7 дней?

 

 

 

Задача  8.Для ремонта квартиры требуется 69 рулонов обоев. Сколько пачек обойного клея нужно купить, если одна пачка клея рассчитана на 7 рулонов?

 

 

Задача  9. Для приготовления маринада для огурцов на 1 литр воды требуется 14 г лимонной кислоты. Лимонная кислота продается в пакетиках по 10 г. Какое наименьшее число пачек нужно купить хозяйке для приготовления 6 литров маринада?

 

Задача  10.Таксист за месяц проехал 6000 км. Цена бензина 23 рублей за литр. Средний расход бензина на 100 км составляет 8 литров. Сколько рублей потратил таксист на бензин за этот месяц?

 

 

 

 

 

 

 

 

Задачи из сборника  заданий ГИА

Задача 1. Велосипедист съездил из села на станцию и вернулся назад. На обратном пути он увеличил скорость на 1 км/ч по сравнению с той, с которой ехал на станцию, и потратил на обратный путь на 8 мин. меньше. С какой скоростью велосипедист ехал на станцию, если расстояние между селом и станцией составляет 32 км?

Решение с объяснением:

Пусть х км- начальная скорость, с которой велосипедист съездил из села на станцию ,тогда обратно он возвращался со скоростью (х+1) км/ч.На всю дорогу он потратил 8 мин, что составляет ч.Расстояние между селом и станцией составляет 32 км. Следовательно,-это время,потраченное  велосипедистом на дорогу из села на станцию, а обратно он потратил меньше, так как скорость увеличил..Разница между ними составляет ч. Составим уравнение.

=                ОДЗ: х=0 и х=-1

=0

+х-240=0

Д=-4*(-240)=1+960=961

Х1==15     х2==-16 не подходит, т.к.скорость не может быть отрицательной.

Ответ: начальная скорость велосипедиста 15  км/ч

 

 

 

 

Задача 2. Мотоциклист проехал 40 км из пункта А в пункт В и вернулся назад. На обратном пути он уменьшил скорость на 10 км/ч по сравнению с начальной и потратил на обратную дорогу на 20 мин. больше. Найдите начальную скорость мотоциклиста.

 

 

Задача 3. На перегоне, длина которого равна 240 км, поезд шел со скоростью на 10 км/ч меньшей, чем должна быть по расписанию, и опоздал на 48 мин. С какой скоростью должен был идти поезд по расписанию?

 

 

 

 

Задача 4. Из села А в село В, расстояние между которыми равно 30 км, велосипедист проехал с некоторой скоростью, а возвращался со скоростью на 3 км/ч большей и потратил на 30 мин. меньше, чем на путь из села А в село В. Найдите первоначальную скорость велосипедиста.

 

 

 

 

 

 

Задача 5. Из города А в город В, расстояние между которыми 80 км, выехал автобус. В середине пути он был задержан на 10 мин., но, увеличив скорость на 20 км/ч, прибыл в город В вовремя. С какой скоростью автобус ехал первую половину пути?

Решение с объяснением:

Пусть х км/ч-скорость ,с которой выехал автобус из города А в город В, тогда (х+20) км/ч-скорость, с которой автобус начал с середины пути после остановки. Расстояние между городами 80км.

Следовательно,-это время, потраченное  автобусом на дорогу до середины пути, а с середины пути  он потратил меньше, так как скорость увеличил..Разница между ними составляет ч. Составим уравнение.

=                ОДЗ: х=0 и х=-20

=0

+20х-4800=0

Д=-4*(-4800)=400+19200=19600

Х1==60     х2==-80 не подходит, т.к.скорость не может быть отрицательной.

Ответ: первую половину пути автобус ехал со скоростью 60  км/ч

 

 

 

 

 

 

Задача 6.Лыжник должен был проехать 10 км, чтобы в назначенное время вернуться в туристический лагерь. В середине пути он задержался на 15 мин., но, увеличив скорость на 10 км/ч, приехал в лагерь вовремя. Какова была первоначальная скорость лыжника?

 

Задача 7. Велосипедист должен был проехать 48 км, чтобы успеть к поезду. Однако он задержался с выездом на 48 мин. Чтобы приехать на станцию вовремя, он ехал со скоростью, на 3 км/ч большей, чем планировал первоначально. С какой скоростью ехал велосипедист?

 

Задача 8. Лодка проплывает 9 км по течению реки и 1 км против течения за то же самое время, которое нужно плоту, чтобы проплыть 4 км по этой реке. Найдите скорость течения, если собственная скорость лодки составляет 8 км/ч.

Решение с объяснением:

Пусть  Х км/ч - скорость течения и плота, тогда
8+х  км/ч - скорость лодки по течению
8-х  км/ч - скорость лодки против течения.

Следовательно,-это время, которое проплыла лодка по течению, а -время , которое проплыла лодка против течения. Всего лодка потратила на весь путь ч. Составим уравнение.

+=             ОДЗ: х=-8 и х=8,х=0

=0

+80х-256=0 

-20х+64=0

Д=-4*64=400-256=144

Х1==16 не подходит    х2==4

Ответ: скорость течения реки 4км/ч

Задача 9. Моторная лодка проплыла 48 км по течению реки и вернулась назад, потратив на обратный путь на 1 ч. больше. Найдите скорость течения, если собственная скорость лодки равна 14 км/ч.

Задача 10. Моторная лодка проплыла 24 км против течения реки и 16 км по течению, потратив на весь путь 3 ч. Найдите скорость лодки в стоячей воде, если скорость течения реки составляет 2км/ч.

Задача 11. Моторная лодка проплыла 9 км по течению реки и 14 км против течения за такое же время, которое понадобится ей, чтобы проплыть 24 км в стоячей воде. Найдите скорость лодки в стоячей воде, если скорость течения составляет 3 км/ч.

 

Задача 12. Тракторист должен был за некоторое время вспахать поле площадью 180 га. Но ежедневно он вспахивал на 2 га больше, чем планировал, и закончил работу на 1 день раньше срока. За сколько дней тракторист вспахал поле?

Решение с объяснением:

Пусть X га/день - плановая производительность тракториста, тогда

(x+2) га/день - его фактическая производительность. Следовательно  -запланированные дни выполнения работы.-дни, за которые тракторист выполнил работу. Составим уравнение.

-=1     ОДЗ: х=-2 и х=0

=0

-2х+360=0

+2х-360=0

Д=-4*(-360)=4+1440=1444

Х1==18 не подходит    х2==-20

180:20=9 дней

Ответ: тракторист вспахал поле за 9 дней.

Задача 13. Для перевозки 60 т груза было заказано некоторое количество грузовиков. Но из-за неисправности двух из них на каждую машину пришлось погрузить на 1 т груза больше, чем планировалось. Сколько машин должно было работать на перевозке груза?

 

Задача14. Тракторист должен был вспахать поле площадью 200 га. Каждый день он вспахивал на 5 га больше, чем планировал, и поэтому закончил работу на 2 дня раньше срока. За сколько дней тракторист вспахал поле?

Задача15. Имеем два сплава меди и цинка. Первый сплав содержит 9%, а второй − 30% цинка. Сколько надо взять килограммов первого сплава и сколько килограммов второго, чтобы получить сплав массой 300 кг, содержащий 23% цинка?

Решение с объяснением:

Пусть надо взять x кг первого сплава, а второго — (300-х) кг. Масса цинка в первом сплаве равна 0,09*х кг, а во втором 0,3*(300-х) кг.
По условию, получен сплав с содержанием цинка 23%, 
т.е. его масса равна 0,23*300=69 кг.
Составим уравнение:
0,09*х+0,3(300-х)=69
0,09х+90 -0,3х =69
-0,21х=69-90
-0,21х=-21
х=-21:(-0,21)
х=100 (кг) - взяли первого сплава
300-100=200 (кг) - взяли второго сплава
Ответ: взяли 100 кг первого сплава и 200 кг второго сплава

 

 

 

 

Задача16. Сколько килограммов 20-процентного и сколько килограммов 50-процентного сплавов меди нужно взять, чтобы получить 30 кг 30процентного сплава?

Задача17. К раствору, содержащему 20 г соли, добавили 100 г воды, после чего концентрация раствора уменьшилась на 10%. Сколько граммов воды содержал раствор первоначально?

 

 

 

 

 

 

 

 

 

 

Улыбнемся, решая задачи!

Задачи от Григория Остера

Остер Григорий Бенционович (р. 1947) – российский детский писатель, драматург, телевизионный ведущий и сценарист. На его книгах выросло уже несколько поколений россиян, а мультфильмы, снятые по сценариям Остера, стали классикой отечественной мультипликации. Это он придумал, что советы бывают не только полезными, но и вредными. С 2007 года писателю присвоено звание Заслуженного деятеля искусств Российской Федерации.

Г.Остер: «Задачи эти как раз для тех, кто математику не любит, привычно считает решение задач тоскливым и нудным трудом. Вот они пусть усомнятся».

Многие известные математики говорят, что главное в математике научить человека мыслить, ставя порою перед ним очень сложные задания. «Математика развивает логическое мышление, умение самостоятельно решать проблемы, способность быстро уловить суть и найти к жизненной задаче наиболее подходящий и простой подход»- говорят нам взрослые.. Математика встречается в нашей жизни практически на каждом шагу и не такая уж она серая и скучная, а разноцветная и веселая...

 

               

                                                           

 

 

Задачи от Григория Остера

 

Задача 1.На кухне площадью в 6 кв.м дедушка рассыпал мелочь. С каждого кв.м бабушка собрала по 45 коп. Каков общий урожай?

Задача 2.Один водитель автобуса сэкономил за месяц 89 литров бензина, а другой вообще никуда не ездил и никого не возил, и сэкономил бензина в 30 раз больше. Узнай, сколько бензина израсходовал за месяц первый водитель, если известно, что обоим водителям выдают одинаковое количество бензина?

 

Задача 3.На одном маленьком квадратном необитаемом острове, длина одной стороны которого была 153 м, обитали 7802 потерпевших кораблекрушение Робинзонов. Узнай, по скольку кв.м пришлось на каждого Робинзона после того, как на остров вылез еще один потерпевший кораблекрушение Робинзон?

 

Задача 4.Путешественник собирался пройти 45 км, но ему помешал маленький гвоздик, торчащий в левом ботинке. Длина гвоздика 1 см. Во сколько раз этот гвоздик короче расстояния, которое не смог из-за него пройти путешественник?

 

Задача 5.Из двух сел, находящихся на расстоянии 16 км, вышли в 9 часов навстречу друг другу и двигаются с одинаковой скоростью 8 км/ч две разговорчивые тетеньки. Сколько часов проговорят тетеньки встретившись, если известно, что расстанутся они в 12 часов?

 

 

Задача 6.Два пассажира в одно и то же время сели в одну и ту же электричку, отправляющуюся к станции Сходня, и двинулись в противоположных направлениях. Скорость первого пассажира, идущего к головному вагону электрички—2 метра в секунду, а второго, идущего к хвостовому вагону—1 метр в секунду. Скорость электрички, в которой идут оба пассажира—64 км 800 м в час. Вычисли скорость, с которой приближается к станции Сходня первый пассажир и скорость, с которой приближается к этой же станции второй пассажир?

Задача 7.Из двух зоопарков, находящихся друг от друга на расстоянии 240 км, сбежали мама слониха и ее сын слоненок. Слониха бежит со скоростью 20 км/ч, а слоненок бежит вдвое медленнее. Через сколько минут они обнимутся, если побегут навстречу друг другу?

 

Задача 8.Петр Петрович нашел кучу денег. Целый год он тратил по 253 рубля в месяц, потом спохватился, что денег хватит еще только на три месяца и то, если тратить по 20 рублей в месяц. А теща Петра Петровича как раз год тому назад потеряла кучу денег, и было в той куче ровно 30096 рублей. Как ты думаешь, не тещину ли кучу нашел Петр Петрович?

 

Задача 9.Лошадь всадника без головы движется обычно со скоростью 12 км/ч. Если бы всадник без головы все время говорил ей: "Но! Пошла!", она помчалась бы с вдвое большей скоростью. За какое время проехали бы они в этом случае расстояние в 72 км?

 

 

 

 

Задача 10.Корабль отошел от берега, 2 часа прошел со скоростью 30 км/ч и утонул. Капитан со своей командой и пассажиры поплыли домой. Капитан и его команда вылезли на берег через 10 часов после кораблекрушения, а пассажиры добирались до суши на 5 часов дольше. С какой скоростью плыл домой капитан со своей командой и с какой плыли пассажиры?

Задача 11.В пятилитровой кастрюле мама сварила 3 литра горохового супа, а потом нечаянно опрокинула туда трехлитровую банку, полную вишневого варенья. Сколько литров вишневого варенья не поместилось в кастрюле горохового супа?

Задача 12.Если в кастрюлю с 5 литрами горохового супа бросить 2 мяча, 4 литра супа выплеснутся. По скольку ложек горохового супа достанется каждому члену семьи, состоящей из 6 человек, если известно, что в 1 литре горохового супа 60 ложек?

Задача 13.У Вовочки было 50 копеек. Он подошел к Васе и отнял у него 3 рубля 50 копеек, а потом подошел к Коле и отнял у него 5 рублей 60 копеек, потом к Феде и отнял 8 рублей 70 копеек. Но тут к Вовочке подошел старшеклассник Егор и отнял у Вовочки вдвое больше денег, чем тот сам отнял у Васи и Коли вместе взятых. Сколько денег теперь осталось у Вовочки?

Задача 14.Пока мама разговаривала по телефону с бабушкой, трехлетняя Маша приготовила праздничный ужин из трех блюд. На первое — суп из 3 л молока, 1 кг сахара и 1 л подсолнечного масла. На второе — пюре из 4 кг мятых помидоров, 250 г молотого кофе и трех рваных булочек по 150 г каждая. На третье — кисель в чайнике из 1 л вишневого сиропа, 400 г маргарина и 600 г нечищеной, но зато очень мелко нарезанной сырой картошки. Сколько килограмм сухих продуктов и сколько литров жидких израсходовала Маша на этот праздничный ужин?

 

Авторские задачи

Задача 1. В 8-А классе БСШ№23 учатся 23 ученика. 17%  всех учащихся класса посещают музыкальную школу; 28% учащихся занимаются танцами ;  7% учащихся  занимаются в спортивных секциях. Сколько учеников отдельно  занимается каждым видом деятельности?

Задача 2. В 2008-2009 учебном году в БСШ№23 на начало года училось 659 человек, а на конец года учащихся слало 555 человек. На сколько процентов  уменьшилось количество учащихся в данной школе?

Задача 3. На Ломовотской шахте в 2011 году работало 824 человека. Из них 95 человек ГРОЗ, а 12%-проходчики.Сколько человек работало проходчиками на шахте?

Задача 4. В 2012-2013 учебном году в БСШ№23 на конец года осталось  472 учащихся,  что составляет 84% от первоначального количества детей. Сколько учащихся было в школе на начало учебного года?

Задача 5.Такси «Вояж» проехал за два дня  400км. В первый день он ехал 4ч со скоростью 60км/ч, во второй день он ехал со скоростью 80км/ч. Сколько часов был в пути автомобилист во второй день?

 

Задача 6.Часть пути до ДК имени Октябрьской Революции дети  шли со скоростью 50 м/мин в течение 6мин. Остальную часть пути они шли со скоростью 80м/мин. На весь путь до ДК они затратил 15мин. Чему равно расстояние до Дворца культуры?

 

Задача 7. В 1913 году население г.Брянки составляло 19 тыс. человек, в 1989 году — 86 тыс. человек, а в 2006 году — около 40 тыс. человек.  На сколько процентов увеличилось количество  человек в 1989 году, и  уменьшилось количество человек в 2006 году?

Задача 8. Расстояние между  Алчевском и Замковкой 16  км. Из Алчевска в Замковку вышел  автобус со скоростью 80 км/ч. Через 2 часа навстречу ему из Замковки  в Алчевск вышел пассажирский поезд со скоростью 60 км/ч. Через какое время они встретятся?

 

Задача 9. Из поселка Краснополье в поселок Криворожье , расстояние между которыми 7 км, выехал автобус. В середине пути он был задержан на 10 мин., но, увеличив скорость на 6 км/ч, прибыл в   Криворожье вовремя. С какой скоростью автобус ехал первую половину пути?

Задача 10. Для ремонта  кабинетов  ДДЮТ требуется 15 рулонов обоев. Сколько пачек обойного клея нужно купить, если одна пачка клея рассчитана на 4 рулона?

Задача 11. Таксист компании «Лада» за месяц проехал 6000 км. Цена бензина 42 рубля за литр. Средний расход бензина на 100 км составляет 9 литров. Сколько рублей потратил таксист на бензин за этот месяц?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ответы на задачи

Задачи на проценты

1)275 рублей                        6)20горшков

2) 20 ручек                           7)20рыбок

3)  563 рубля                        8)80%

4)192мальчика                     9)19%

5) 3000рублей                      10)20%груш

Задачи на концентрацию, смеси и сплавы

 1)150грамм,450грамм          6) 60грамм

2) 21%                                   7) 30грамм

3)  60кг                                  8)100

4)9кг                                       9)21%

5)на 100кг                               10) 5%  

Задачи на процентное содержание компонентов  в различных  веществах

1) 84%                     

2) 3,45кг белка, 8,25 кг крахиала,0,27 кг жира                         

3)  теряют половину веса                      

4) 4кг                  

5) 10кг

  Задачи на проценты в ЖКХ и на различные виды услуг

1) 90копеек                   

2) в 3 раза

3) на 84 рубля                     

4) 1056рублей                  

5) 312рублей

Задачи на движение в одном направлении и вдогонку

1)2ч 40мин                       

2) 5часов

3)60метров

 4)680метров

5)3часа

6)88км/ч

7)240км

Задачи на встречное движение

1)8часов             5) 5 м/сек          

2) 5часов            6) 225км

3)680км              7)36км

4)24км                8)6часов

Задачи на противоположное движение

1) 720 км/ч               6)5часов

2) 680км                   7)6 км/ч

3)85км                      8)70 км/ч

 4)360км                   9)45км

5)3часа                     10) 4 часа

Задачи на движение по реке

1) 37 км/ч 

2) 78 и 60км

3) 13 км/ч. 

 4)56км за 7ч

5) 26 км/ч 

 Жизненные задачи

1)четверг                               6)10 рублей

2) 21 раз                                7)80кг

3)  57мест                             8)10рулонов

4)8сырков                             9)6пачек

5) на 105руб больше           10) 11040рублей

Задачи из сборника  заданий ГИА

2) 40км/ч                                10) 14км/ч

3) 90 км/ч                                11) 24км/ч

4)  12 км/ч                               13) 12машин

6) 10 км/ч                                14)10 дней

7) 15 км/ч                                16) 20кг и 10кг

9) 2 км/ч                                  17)80 грамм

Задачи от Григория Остера

1)  4 рубля 50 копеек                8) 3096 долларов                     

2) 2581литр                                9) 3ч

3)                                          10) 50км/ч

4)в 450000раз                             11)1 литр                     

5)14часов                                    12) 3 литра

6)72 км/ч  и 61,2км/ч                 13) 10копеек                         

7)через 8 часов                           14)  600 гр сухих и 5 л жидких