Считай быстро (метод Оконешникова)

Министерство образования, науки и молодёжи Республики Крым

 

Республиканский конкурс  «Я - исследователь»

 

 

 

Секция: Математика

 

 

 

 

 

УМНОЖАЙ БЫСТРО

  (НА ПРИМЕРЕ ТАБЛИЦЫ УМНОЖЕНИЯ В.ОКОНЕШНИКОВА)

 

 

 

 

 

 

Работу выполнил

Шеихмамбетов Алим Нариманович,

обучающейся 3-Б класса

муниципального бюджетного

общеобразовательного учреждения

«Заветненская С Ш им. Крымских партизан»

Советского района

 

Научный руководитель:

Распутько Любовь Федоровна,

учитель начальных классов

муниципального бюджетного

общеобразовательного учреждения

«Заветненская С Ш им. Крымских партизан»

Советского района

 

 

 

с. Заветное− 2019

 

 

 

 

СОДЕРЖАНИЕ

 

ВВЕДЕНИЕ………………………………………………………………….	3
ГЛАВА 1. История создания таблицы умножения……….	5
1.1 Древние варианты таблицы  умножения……………………………..	5
1.2 Таблица Пифагора………………………………………………………	7
ГЛАВА 2.  Таблица умножения В. Оконешникова………..	9
ГЛАВА 3. Практическая часть……….……………………………	11
3.1 Умножение чисел при помощи таблица умножения В. Оконешникова……………………………………………………………..	11
3.2 Анкетирование и оформление результатов…………………………….	12
Заключение……………………………………………………………	14
Список литературы…………………….…………………………	15
Приложения

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ВВЕДЕНИЕ

 

«Предмет математики настолько серьезен, что полезно не упускать, случаев делать его немного занимательным». 
Б. Паскаль

 

Можно ли представить мир без чисел? Без чисел ни покупки не сделаешь, ни времени не узнаешь, ни номера телефона не наберёшь. Человеку в повседневной жизни невозможно обойтись без вычислений. Поэтому на уроках математики, нас в первую очередь учат выполнять действия над числами, то есть считать. Умножаем, делим, складываем и вычитаем мы привычными для всех способами, которые изучаются в школе.

Мне стало интересно, а есть ли еще какой-нибудь способ вычислений? Оказалось, что можно умножать не только так, как предлагают нам в учебнике математики, но и по-другому.

Объект исследования: нестандартный способ умножения чисел.

Предмет исследования: таблица умножения В. Оконешникова.

Актуальность проблемы заключается в том, что использование нестандартного приема  в формировании вычислительных навыков усиливает интерес к математике.

Целью данной работы является исследование нестандартного способа умножения чисел В. Оконешникова.

Гипотеза: Если использовать нестандартный приём решения примеров на умножение по В. Оконешникову, то предмет  математики будет  занимательным и интересным.

Задачи исследования:

•    изучить историю создания таблицы умножения;

•    познакомиться с нестандартным способом умножения;

•    продемонстрировать преимущества нестандартного способа умножения;

•    познакомить одноклассников  с нетрадиционным способом умножения.

Методы исследования:

- изучения справочной литературы  и  ресурсов Интернета;

- изучение и обобщение отечественной практики;

- сравнение, анализ, синтез;

- обобщение;

- выполнение практической работы.  

Этапы исследования: 

1-й этап. Подготовительный. Изучение проблемы, актуальность, разработка мероприятий.

2-й этап. Основной. (Сбор информации о способе умножения, поиск интересных фактов, проведение практической работы). 

3-й этап. Заключительный. Подведение итогов, оформление работы. Представление работы на районный конкурс «Я - исследователь».

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ГЛАВА 1. История создания таблицы умножения

 

1.1 Древние варианты таблицы  умножения

 

Привычная для нас таблица умножения это 8 столбцов с последовательными примерами на задней обложке тетрадки.

Таблицу умножения еще называют «Таблицей Пифагора», особенно когда она представлена в виде квадрата, стороны которого — множители, а в ячейках стоит их произведение. Так принято считать в европейской культуре. Но интересен тот факт, что никаких письменных свидетельств тому, что именно Пифагору принадлежит авторство таблицы. Существуют только косвенные доказательства. Последователь его учения — Никомах Герасский, который жил на рубеже I и II веков нашей эры, записал таблицу в привычном нам виде в своем сочинении «Введение в арифметику». Он утверждал, что авторство принадлежит древнегреческому ученому Пифагору.

Впоследствии, в 493 году ученый Викторий Аквитанский записал таблицу из 98 столбцов, которая представляла в римских числах результат перемножения чисел от 2 до 50. А в 1820-м году шотландский физик и профессор математики Джон Лесли в своей книге «Философия арифметики» опубликовал таблицу умножения до 99. И он же стал рекомендовать ученикам заучивать ее.

Известно, что впервые таблица умножения была введена в школах в средневековой Англии. Выглядела она, как система перемножения чисел до 12. В Англии до сих пор сохранился именно такой средневековый вариант.

Таким образом, мы видим, что таблица не во всех странах одинакова. Например, в Индии, она включает в себя числа до 20-ти.
Мнения ученых по поводу авторства таблицы умножения разделились. И многие считают, что Пифагор не может быть ее создателем. Так как есть факты, подтверждающие другое происхождение.

Самая старая десятиричная таблица умножения найдена на раскопках древних китайских городов. Ученые датируют ее 305 г. до н.э.

При раскопках в Японии города Нара нашли дощечку с фрагментами записей, которые подтверждают, что в древней Японии вели подсчеты с помощью таблицы. Интересно то, что иероглифы похожи на древнекитайское письмо. Это не единичный случай обнаружения подобных табличек археологами. Подобную дощечку нашли на раскопках еще одной японской столицы Хэйнан. Таким образом, ученые предполагают, что таблица умножения могла попасть из Китая в Японию, так как между двумя империями были очень прочные торговые отношения. По мнению ученых, таблица умножения, которую придумали в Китае, могла попасть в Индию вместе с торговыми караванами, а затем уже распространиться по Азии и Европе. Но есть и еще одна версия- таблица была изобретена в Месопотамии. Эта версия тоже подтверждается находками археологов. Самая старейшая табличка была найдена на раскопках древнего Вавилона и имеет возраст около 4000 лет. Выглядит она, как глиняная дощечка с клинописью. В ее основе шестидесятеричная система исчисления. Можно предполагать, что таблица была изобретена параллельно в нескольких империях, так как люди постоянно сталкивались с необходимостью делать подсчеты.

Интересно, что на Руси существовал крестьянский способ умножения, который заключался в том, что первый множитель увеличивается в два раза, а второй уменьшается тоже в два раза. И эта операция продолжалась до тех пор, пока второй множитель не становился равен одному. Строки, в которых правое число четно, удалялись, а сумма левых чисел и оставшихся строк давали нужный результат. В Россию таблица попала благодаря математику Леонтию Филипповичу Магницкому, который издал в 1707 году первый учебник по математике «Арифметика». В этом учебнике были таблицы сложения и умножения.

1.2 Таблица Пифагора

 

Таблица умножения Пифагора известна с древности. Ее создание, как следует из названия, приписывают древнегреческому философу и математику Пифагору и его ученикам.

Таблица умножения Пифагора представляет собой квадрат, на левой и верхней гранях которого расположены числа от 1 до 10 (Приложение 1).

Размеры таблицы 1-10 не являются конечными, расширить таблицу можно до бесконечности.

На главной диагонали, выделенной серым цветом, расположены квадраты чисел, а произведение двух разных чисел находится на их пересечении. В таблице Пифагора достаточно много закономерностей, на эту тему достаточно много информации в сети. Однако, большая часть этих закономерностей слишком сложна даже взрослого человека, если рассматривать их практическое применение. Поэтому выделим всего 3 из них:

·        Как упоминалось выше, по главной диагонали расположены квадраты чисел.

·        Таблица симметрична.

·        Каждый следующий столбец (строка) – это результат сложения предыдущего столбца (строки) на число в левой (верхней) грани квадрата.

С помощью этих свойств легче объяснить принцип умножения, что, по сути, это многократное сложение. В целом таблица Пифагора хороша в теоретическом плане на начальном этапе, но для практики ее лучше дополнить другими методами, лучше всех логическим.

Преимущества:

·        Краткость. Таблица Пифагора куда меньше, чем таблица из столбцов.

·        Наглядность. Из таблицы хорошо понятен принцип умножения и его свойства.

ГЛАВА 2.  Таблица умножения В. Оконешникова

 

Автором привычного для нас способа умножения  следует считать Адама Ризе, популярного немецкого педагога (1492–1559).  Теперь этот способ  считается самым удобным. Главное отличие способа Адама Ризе заключается в том, что разряды всех чисел и множимого, и множителя, и произведения стоят один под другим в одном вертикальном столбце; благодаря этому сразу видно, к какому разряду принадлежит известная цифра, и, следовательно, сбиться в этом почти нельзя.

Шло время. В ходу появилось одновременно множество  различных способов умножения.

Кандидат философских наук Василий Оконешников, по совместительству изобретатель новой системы устного счёта, считает, что школьники смогут научиться устно, складывать и умножать миллионы.
По мысли учёного, прежде чем стать вычислительным «компьютером», необходимо вызубрить созданную им таблицу. Цифры в ней  расположены в девяти клетках неспроста. Как утверждает Василий Оконешников, глаз человека и его память  устроен так хитро, что информация, расположенная по его методике, запоминается, во-первых, быстрее, а, во-вторых, намертво. По мнению самого учёного, наиболее выигрышной в этом отношении является девятеричная система – все данные просто располагают в девяти ячейках, расположенных, как кнопочки на калькуляторе.

Таблица умножения разделена на 9 частей. Расположены они по принципу кнопок калькулятора: слева в нижнем углу «1», справа в верхнем углу «9». Каждая часть – таблица умножения чисел от 1 до 9 (по той же «кнопочной» система).     Для того, чтобы умножить любое число, например, на 8, мы находим большой квадрат, соответствующий числу 8 и выписываем из этого квадрата числа, соответствующие цифрам многозначного множителя. Полученные числа складываем особо: первая цифра остаётся без изменения, а все остальные попарно складываются. Получившееся число и будет результатом умножения.  Если при сложении двух цифр получается число, превосходящее девять, то его первая цифра прибавляется к предыдущей цифре результата, а вторая пишется на «своё» место (Приложение 2).

С помощью таблицы Оконешникова, по утверждению самого автора, можно изучить и иностранный язык, и даже таблицу Менделеева,
Новая методика была опробована в нескольких российских школах и университетах. Минобразования РФ разрешило публиковать в тетрадях в клеточку вместе с привычной таблицей Пифагора новую таблицу умножения – пока просто для знакомства.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ГЛАВА 3. Практическая часть

 

 

3.1 Умножение чисел при помощи таблица умножения В. Оконешникова

 

Для умножения чисел данным способом мне понадобилась:

-таблица Оконешникова,

-лист бумаги,

-ручка.

Умножим 24 на 7, получим 2*7=14; 4*7=28, т.е. мы получим 14,28. Первую цифру  1 оставляем без   изменения, 4+2=6, последняя  цифра без изменений. Результат получаем 168.

                 Можем умножать и большие числа.

Умножим  367 на 5, получим  3*5= 15; 6*5= 30; 7*5= 35, т.е. мы получим 15, 30, 35.

 Первую цифру  1 оставляем без изменения, 5 и 3 складываем =8, 0 и 3 складываем =3 ,последняя цифра без изменений.  В результате  получаем 1835.

Умножим  178 на 7, получим 1*7=07; 7*7= 49; 8*7= 56, получим 07, 49,56. Я предлагаю  считать с конца: число 6 –оставляем как есть, к  9 + 5 =14,   7 + 4 =11 +1 =12, число 1 переносим к 0= 1. Получаем результат 1246.

Умножим 965 на 4, получим  36  24  20. Складываем числа = 3860

( Приложение 3).

 

 

 

 

 

 

 

 

 

 

3.2 Анкетирование и оформление результатов

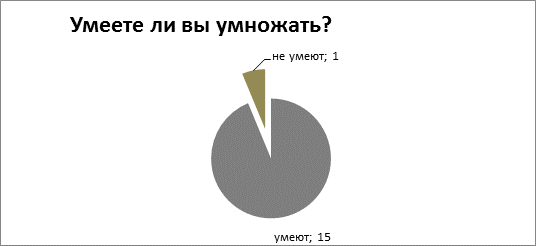
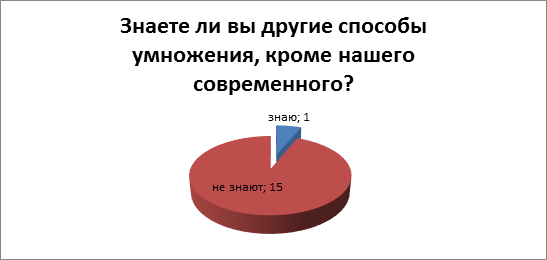
Было проведено анкетирование третьеклассников. Приняли участие 16 человек. На основании анкетирования выявлено, что большинство умеют умножать традиционным способом. А вот о нетрадиционном способе умножения  ребята не знают. (Приложение 4)

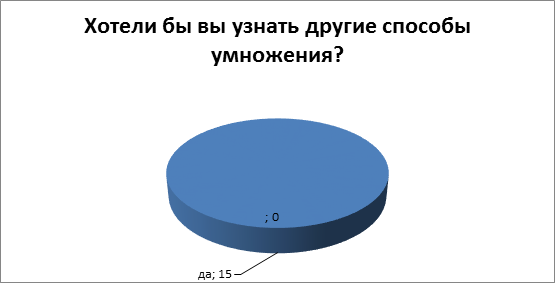
И есть желающие познакомиться с ними. После анкетирования было проведено внеклассное занятие, на котором ребята познакомились  с методом умножения В.Оконешникова. После чего был проведен опрос с целью, выявить, понравился ли этот способ умножения.  Ребятам понравился   современный метод Василия Оконешникова (Приложение 5).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ЗАКЛЮЧЕНИЕ

 

Наша гипотеза о том, что «если использовать нестандартный приём решения примеров на умножение по В. Оконешникову, то предмет  математики будет  занимательным и интересным», полностью подтвердилась.

Выполнив исследовательскую работу, я узнал об истории создания таблицы умножения и умножение чисел с помощью таблицы В. Оконешникова.

 Способ очень удобный, но нужно выучить наизусть  или всегда иметь под рукой таблицу В. Оконешникова. Можно пользоваться  обычной таблицей умножения, а числа записывать по методу В. Оконешникова и тогда получаем быстрый результат.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

СПИСОК ЛИТЕРАТУРЫ

1. Арутюнян Е., Левитас Г. Занимательная математика. - М.: АСТ - ПРЕСС, 1999. - 368 с.
2. Беллюстина В. Как постепенно дошли люди до настоящей арифметики. - ЛКИ ,2012.-208 с.
3. Депман И. Рассказы о математике. – Ленинград.: Просвещение, 1954. – 140
4. Ликум А. Все обо всем. Т. 2. - М.: Филологическое общество «Слово», 1993. - 512 с.
1.5. Олехник С. Н., Нестеренко Ю. В., Потапов М. К.. Старинные занимательные задачи. – М.: Наука. Главная редакция физико-математической литературы, 1985. – 160 с.
6. Перельман Я.И. Занимательная арифметика. - М.: Русанова, 1994 – 205с.
7. Перельман Я.И. Быстрый счет. Тридцать простых приемов устного счета. Л.: Лениздат, 1941 — 12 с. 
8. Савин А.П. Математические миниатюры. Занимательная математика для детей. - М.: Детская литература, 1998 - 175 с.
9. Энциклопедия для детей. Математика. – М.: Аванта +, 2003. – 688 с.

10. Я познаю мир: Детская энциклопедия: Математика/ сост. Савин А.П., Станцо В.В., Котова А.Ю. - М.: ООО «Издательство АСТ», 2000. - 480 с.

11. Шульгина В. П. Методическая копилка/ учеб. пособие; изд-е 2-е. – Ростов н/Д: изд-во «Феникс» 2002-2003.
2. Другие источники информации
Интернет – ресурсы: 

1. История создания таблицы умножения [Электронный ресурс]. Режим доступа:https://tablica-umnozhenia.ru/stati/istoriya-sozdaniya-tablitsy-umnozheniya-2/

2. Таблица умножения Пифагора [Электронный ресурс]. Режим доступа: https://tablica-umnozhenia.ru/kak-bystro-vyuchit/tablitsa-pifagora/

 

ПРИЛОЖЕНИЯ

Приложение 1

Таблица Пифагора

 

 

 

 

 

 

 

 

 

 

 

 

 

Приложение 2

Таблица Оконешникова

49	56	63	56	64	72	63	72	81
28	35	42	32	40	48	36	45	54
07	14	21	08	16	24	09	18	27
28	32	36	35	40	45	42	48	54
16	20	24	20	25	30	24	30	36
04	08	12	05	10	15	06	12	18
07	08	09	14	16	18	21	24	27
04	05	06	08	10	12	12	15	18
01	02	03	02	04	06	03	06	09

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Приложение 3

 

 

Приложение 4

 

Приложение 5

Результаты анкетирования

 

 

 

Скачано с www.znanio.ru