Для чего нужно изучать математику???  Алексеева О.А.  и учащиеся 8 А класса
	Для чего нужно изучать математику???

РОЛЬ МАТЕМАТИКИ В ЖИЗНИ ЧЕЛОВЕКА

«Тот, кто не знает математики, не может узнать ни какой другой науки даже не может обнаружить своего невежества»

Обратите внимание: •   «Великая книга природы написана математическими символами»  •   «В каждой естественной науке заключено столько истины, сколь в ней есть математики»  •   «Кто с детских лет занимается математикой, тот развивает внимание,  тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели»

В этом выпуске:

Зачем ребенку учить 1-2

математику?

Математика и воен-   2

ное дело

Математика и искус- 3

Математика в нашей жизни присутствует не только в процессе освоения профессии и реализации полученных знаний. Так или иначе мы используем царицу наук практически в каждый момент времени. Именно поэтому математике начинают обучать достаточно рано. Решая простые и сложные задачи, ребенок не просто учится складывать, вычитать и умножать. Он медленно, с азов постигает устройство современного мира. И речь тут идет не о техническом прогрессе или умении проверять сдачу в магазине. Математика формирует некоторые особенности мышления и оказывает влияние на отношение к миру.

Наверное, все вспомнят хотя бы один вечер за домашним заданием, когда хотелось отчаянно взвыть: «Я не понимаю, для чего нужна математика!», отбросить в сторону ненавистные сложные и нудные задачки и сбежать во двор к друзьям. 

Именно математика, а затем и физика, учит находить причинно-следственные связи, закладывает привычку искать пресловутое «откуда ноги растут». Внимание, сосредоточенность, сила воли — они также тренируются в процессе решения тех самых ненавистных задачек. Если пойти дальше, то умение выводить следствия из фактов, прогнозировать будущие события, а также привычка это делать тоже закладываются во время изучения математических теорий. Моделирование, абстрагирование, дедукция и индукция — все это методы царицы наук и одновременно способы работы мозга с информацией.

Часто именно математика дарит ребенку откровение, что взрослые не всемогущи и знают далеко не все. Так бывает, когда мама или папа на просьбу помочь решить задачку лишь разводят руками и объявляют о своей неспособности это сделать. И ребенок вынужден сам искать ответ, ошибаться и снова искать. Бывает и так, что родители просто отказываются помочь. «Ты должен сам», — говорят они. И правильно делают. После многочасовых попыток ребенок получит не просто сделанное домашнее задание, но способность самостоятельно находить решения, обнаруживать и исправлять ошибки. И в этом также кроется роль математики в жизни человека.

Конечно, самостоятельность, умение принимать решения, отвечать за них, отсутствие страха перед ошибками вырабатываются не только на уроках математики. Математика воспитывает такие качества, как целеустремленность и активность. Правда, многое зависит и от учителя. Неправильная подача материала, излишняя строгость и давление могут, наоборот, привить страх перед трудностями и ошибками  нежелание высказывать свое мнение, пассивность. Математика в жизни общества и отдельного человека затрагивает огромное количество областей. Некоторые профессии без нее немыслимы, многие появились только благодаря развитию отдельных ее направлений. Современный технический прогресс тесно связан с усложнением и развитием математического аппарата. Компьютеры и телефоны, самолеты и космические аппараты никогда бы не появились, не будь людям известна царица наук. Однако роль математики в жизни человека этим не исчер-

ство

Математика и живо- 4 пись

Математика и музыка 5

Математика и кули- 6

нария

          

Зачем ребенку учить математику? 

Жизнь – сложный лабиринт, головоломка, постоянная череда задач, которые нужно решать. Математика формирует умение думать, отстаивать свои мысли, развивает рационалистический стиль мышления. Она учит ставить перед собой задачи, четко планировать их выполнение и обязательно добиться результата. Разве мы не хотим, чтобы наши дети обладали такими умениями и навыками? Разве не наша цель научить их быть целеустремленными, настойчивыми, добиваться поставленных целей?

Зачем ребенку учить математику? (продолжение)

Ведь знания математики нужны в любой профессии, даже, на первый взгляд, далекой от

ки, при выборе будущей профессии придется сразу вычеркнуть те специальности,

ют правило золотого сечения:
самый важный элемент располагается на определенном расстоянии от границ картины. Если ребенок не приложит усилий в освоение математи-	терпение, сосредоточенность, организованность, силу воли, умение решать проблемы за определенный отрезок времени, т.е. математика формирует характер успешного человека.

необходимости точных вычис- которые предполагают какиелений. Например, кажется, то расчеты, использование что она совершенно чужда формул, аналитики, информахудожникам. Но для того, что- тики. А это существенно сузит бы начать писать картину, возможный выбор ребенка. нужно продумать правильное размещение задуманного на

Математика развивает ум, полотне. А для этого использу-

^{память, образное мышление,}

Начало использования мате- «Тяжело в учении— матических знаний в воен-ном деле относится к глуболегко в бою»  кой древности. Известно, что в Древнем Вавилоне арифме- Александр Васильевич тические сведения употребля-лись при подсчете необходи- Суворов мых запасов для армии, геометрия же использовалась при строительстве укрепле-

ских сочинений по артиллерии: «… начальное, во – первых, орудие, еще пушкарю подобает при себе имети – есть циркуль». Для создания армии, в начале XX века, необходимо было наряду с подготовкой командного состава, решить ряд научных и инженерно – технических

Математика и военное дело

ний и подсчете объема необ- проблем. Проблемы артиллеходимых земельных работ. рии по–прежнему оставались

решающими. Но наряду с

В знаменитом диалоге Платоними появились задачи, свя-

на «Государство» говорится о занные с созданием соб-

том, что арифметика и геоственной авиации, бронетан-

метрия необходимы каждому ковых                сил,         организацией

воину. Мы хорошо знаем, что проводной и радиосвязи. Они

создание математического требовали не только привле-

анализа – дифференциальночения известных и уже хоро-

го и интегрального исчисле-

                                                                                                                        шо разработанных математи-

ний – в значительной мере ческих методов, но и созда-

было связано с задачами, ния новых методов исследо-

выдвинутыми артиллерией, и вания.

Стр. 2

Для чего нужно изучать математику???

что позднее, в свою очередь, развитие новой математики В ту пору на первом месте оказывало огромное влияние стояли проблемы, связанные на прогресс самой артилле- с полетом самолета. Теория рии. Во все времена счита- полета позволила рассчитылось, что артиллерийский вать аэродинамические свойофицер одновременно явля- ства конструкций до их поется хорошим знатоком мате- стройки и испытания в воздуматики. В этом плане пре- хе. Эту работу возглавил выкрасное утверждение выска- дающийся ученый Н.Е. Жузано в одном из древнерус- ковский (1847-1921). Он и Нельзя оценивать значимость изучения математики только тем, насколько она нужна нам в быту. Если исходить из такой точки зрения, то достаточно научиться простым математическим действиям: сложению, вычитанию, умножению и делению. Все остальное – ненужные, лишние знания, воспринимаемые многими родителями и детьми как прихоть создателей школьной программы, авторов учебников и преподавателей. его ученики положили начало замечательному учреждению, получившему позднее наименование ЦАГИ (Центральный аэрогидродинамический институт).

В связи с исследованием механики полета при больших скоростях М.А. Лаврентьев разработал новую математическую теорию квазианалитических функций, позволяющую учитывать сжимаемость воздуха. С глубокой древности в военном деле применялись различные способы передачи информации, в том числе и такие, которые не доступны для понимания противником. История использования различного рода кодов для шифровки сообщений насчитывает тысячелетия. Вспомним, что математику Ф. Виету(1540-1603) удавалось с большой легкостью разгадывать шифры, использовавшиеся испанским королем для передачи секретных сведений, направляемых посланнику при французском дворе и некоторым другим лицам.

Само собой разумеется, что

для передачи секретных сведений, направляемых посланнику при французском дворе и некоторым другим лицам. Само собой разумеется, что эти вопросы в наши дни заняли несравненно большее значение. В последние десятилетия к проблемам шифрования и дешифрования широко привлекаются математики, особенно специалисты в области комбинаторики, математической логики, алгебры.

Послевоенный период начался в военном деле тремя событиями исключительной важности: появлением ядерного оружия, созданием электронных вычислительных машин и широким развитием работ по ракетной технике. Каждое из указанных направлений конструкторской мысли столкнулось с необходимостью самого широкого привлечения к соответствующим разработкам представителей теоретических областей знания, в первую очередь физиков и математиков.

Математика и искусство

В современной армии не

только командиру, но и солдату для того, чтобы успешно справляться со своими обязанностями, нужно владеть основами электротехники, радиотехники, ХОРОШО ЗНАТЬ МАТЕМАТИКУ,

К архитектуре во все времена было три требования – целесообразность, крепость и красота. Никто не обустроит   себе спальню в высоком зале, а для танцевального вечера не выберет комнатку. Стадион, театр, библиотека отличаются один от другого и внешним видом, и внутренним обустройством. Целесообразность – обязательное соответствие строения своему предназначению.

О крепости архитектурных сооружений хорошо сказано в сказке про трех поросят. Красота, гармония в разные века была разной. В Египте строили колоннами (зал в Корнаке). Колонны стоят близко, огромные, высокие. В таком «лесу» хорошо пугать. Так же строили греки. Балка, балка, а сверху перекрытие. Такие строения могли расти в длину и ширину.

Для чего нужно изучать математику???

Стр. 3

Поставим руки локтями на стол и переплетем пальцы рук,- выйдет арка. Место переплетения рук – замок арки. Надавите подбородком на него- и почувствуете легкую боль в локтях. Давление по арке распределяется во все стороны и позволяет строить второй этаж. Более того, ряды полукруглых арок позволяют строить полукруглый свод(Колизей). 

В начале такие сооружения не имели потолка, т.к. не была решена главная математическая задача: как покрыть круглый дом? И вот в конце 50-х годов прошлого века профессор Московского архитектурного института М.С.Туполев разработал конструкцию кристаллических куполов, которые состоят из равносторонних многоугольных пластин.

Отрасль использования куполов разнообразная. Их можно использовать и как выставочные павильоны, торговые залы, кафе, рестораны и т.д. Размеры помещений не ограничены. Так, в г. Истра под Москвой построен купол с пролетом в 237 метров. В таком сооружении можно разместить целый микрорайон. Идея использования кристаллических куполов позволяет строить гигантские 60метровые круглые дома. Пример – выставочный Центр во Флориде. 

Архитектура сегодня движется в двух направлениях: конструирование необходимых форм на основе математических методов и  заимствование этих форм у живой природы. 

«В математике есть своя красо-

та, как в живописи и поэзии»

(Н.Е. Жуковский)

Архитектура второго направ- Видите? Шарики похожи на ления теряет поэзию прямого пчелиные соты.

угла, принимая легкие округ-

Архитектурная бионика рас-

лые очертания. Но их нужно сматривает все: паутину пау-

вычислить. На помощь прихока, крыло Кажана -и возника-

дит геометрия. Она - посредют тенты на гнущемся конту-

ник между природой и архире; симметрию цветов, мор-

тектурой. В чем же секрет ских звезд – возникает,

гармонии природных форм? например, дом оперного теат-

Мы знаем, что прямая – кратра в Сиднее; раскроют рако-

чайшее расстояние между вины моллюсков – и получа-

двумя точками, а шар – комют купол выставочного зала в

пактнейшая геометрическая

Эйндховене (Голландия).

форма. Почему же в живой природе они не встречаются? Форма крыльев бабочки Зато они встречаются в своих вдохновляют архитекторов на производных. Наполните ша- создание аэропорта в Ньюрик водой и положите на стол Йорке.

- он станет похож, но морско-

Архитектурная бионика имеет го ежа. Возьмите несколько древние корни. Р. Декарт на одинаковых шариков, полоосновании метода координат жите на ровную поверхность изучал кривую, которая полутак, чтобы они касались друг чила название  друга, а сверху положите прозрачное стекло. Придавите.

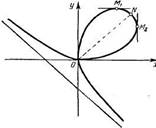
 «Лепесток жасмина», ее уравнение х + у = 3аху. В 18 столетии итальянский геометр Г. Гранди описал уравнениями семейство цветов.

Немецкий математик Б. Хабенихт получил уравнение листьев, плодов, жуков.

Архитектурная бионика еще только начинает свой путь. Но уже сейчас понятно, что это перспективное направление в архитектуре.

Математика и живопись

Стр. 4

Для чего нужно изучать математику???

щенной геометрической схеме. Чаще всего художественные полотна создаются на основе двух геометрических конструкций – «золотого сече-

Архитекторы древности знали, что от домов, построенных по такому правилу, веет теплом и покоем. Наоборот, ощу-

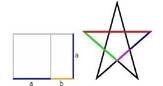
Геометрические мотивы не- CB: AC. (см. выше)   редко присутствуют в картинах известных художников. Хотя художник часто действует интуитивно, а искусствовед – сводит весь художественный арсенал картины к упро-

образованную точкой, которая движется от начала координат (по заданному закону) и равномерно вокруг своего начала. (См.

 

 

 

 

Перед нами две картины –

« К о р а б е л ь н ы й        л е с »

И.И.Шишкина и «Избиение младенцев» Рафаэля Санти: одна дышит покоем и гармонией, другая вызывает тревогу, желание куда-то спрятаться.

Видите, сосну, которая стоит на переднем плане? Она визуально делит картину на два фрагмента – яркую залитую солнцем поляну и полутень. Если измерять картину, то выйдет, что длина картины к сосне так относится к длине всей картины, как меньшее расстояние до сосны к большему. Каждый из фрагментов картины построен по тому же принципу. Вот откуда этот уравновешенный характер. Обратимся к картине Рафаэля и найдем ее центр, т.е. наиболее драматический эпизод. Это женщина с левой стороны, которая закрывает

 

Для чего нужно изучать математику???			Стр. 5
им полем деятельности для высокоталантливого человека. Пифагор был математиком, врачом, музыкантом, моралистом, мм политиком.  От Пифагора до Канта почти все философы были математиками. Р. Декарт занимался философией, музыкой, фехтованием, астрономией, физикой, математикой. Гаусс был в поисках между математикой и филологией. Леонардо да Винчи казалось, что тайны и глубины мира могут быть воплощены только в живописи, в 18ст. считали, что только в музыке, в 19ст. – только в литературе, в 20ст. – только в науке. Однако есть универсальные люди, способные проявить свой талант сразу в нескольких сферах. Математика и музыка Английский математик Д. Сильвестр писал:» Музыкаматематика чувств, а математика-музыка разума». Впервые математически описал звук Пифагор. Его целиком можно назвать прадедом акустики. Пифагор мыслил приблизительно так: целая струна звучит как» до», половина- «ре», треть- «ми», четверть- «фа». Конечно на современную гамму это не похоже, Пифагор пошел далее. Его октава стала выражаться так: Потом он ввел еще несколько дополнительных звуков (бемоли, диезы в современном понимании). Прослушав интервалы, выявилось, что лучше всех звучит квинта (ее соотношение 2:3), и вывел формулу ряда звуков. Математика помогает мастеру создавать музыкальные инструменты. Простейшая сопилка делается так: на половине длины	сверлят дырочку = «до», на трети – «ре», на четверти – «ми». А колокольчики. Возраст старейших валдайских колокольчиков неизменных спутников Пушкина в дороге,200 лет. Когда они появились впервые, неизвестно. Но их изображения есть уже на картинах 16ст. Сначала они качались всем корпусом, а потом стали тяжелеть: мастера сделали их неподвижными, а раскачивался только язычок. Как можно достичь того чтобы звон имел красивый звук и тот же тон, независимо от того, маленькие они или большие? В конце70-х годов в Москве раскрыли секрет красивого звука. Колокол должен содержать 81,94% меди,17,21% олова,0,035% серы. Также вычислили, что в основе формы колокола лежит равнобедренный треугольник со сторонами, которые составляют золотую пропорцию. Есть даже целая наука о колоколах, и называется она компанология.	В понимании Пифагора каждая планета звучит в космосе, как какая-то нота. Например, Солнце – «до», Луна – «фа». Его          взгляды разделял                 И. Кеплер, который видел в мироздании оркестр Солнечной системы, которое неслышно для человека исполняет вселенскую симфонию. Можно сказать, что сейчас фантазия Кеплера реализовал а с ь                 в              п у л ь с а р а х (космические источники радио-,оптического, рентгеновского, гамма-излучений, приходящих на Землю в виде периодически повторяющихся всплесков) – пять из них неожиданно звучат аккордом. Пульсары – нейтронные звезды, которые быстро вращаются и блеск которых периодически меняется. В 1987 году открыли миллисекундные пульсары. Их частота соответствует музыкальным звукам в пределах клавиатуры рояля. Пульсар 1937+21 поет мибемоль второй октавы, а пуль- сар 1953+29 – ми малой октавы.

Математика и кулинария

«CULINARIUS» – в Древнем Риме «искусство приготовления пищи». На самом деле, все этапы приготовления пищи, в том числе покупка продуктов питания, израсходование бюджета требуют некоторые математические знания. Математика в кулинарии имеет большое значение, так как для приготовления любого блюда должен соблюдаться рецепт. В рецепте указывается точное соотношение продуктов, которое необходимо соблюдать в процессе приготовления. При взвешивании продуктов в кулинарии используются математические величины масса и объём. Единицы времени играют далеко не последнюю роль в приготовлении блюд. Приготовленные блюда нужно умело делить на порции, в чём нам опять же поможет математика. Нужно знать и владеть приёмами устных вычислений, уметь составлять план – меню, знать рецептуру блюд.

Преобразования. Как в математике, так и в кулинарии мы используем преобразования. Многие рецепты написаны в имперских единицах. Некоторые новые рецепты и измерительные приборы обозначены в метрических единицах (например, миллилитры).

Если в рецепте даётся ½ чашки сливочного масла, а в вашем приборе измерение в

мл, то здесь следует использовать преобразование. Применяем эту формулу перевода: 1 чашка = 237mL. Это означает, что ½ чашки = 118.5mL.

Приведение       к        единице.

Например, для пирога из 4-х яиц надо 180г муки, 120г сахара и 80г масла. А сколько продуктов надо для пирога из трех яиц? Для этого мы сначала вычислим, сколько нужно продуктов, если мы готовим пирог из одного яйца, мы делим все ингредиенты на четыре. После этого мы умножаем все ингредиенты на три и получаем количество граммов продуктов для приготовления пирога из трех яиц.

Эстетикам и математика в кулинарии. Стоит нам подумать о еде, как сразу же, мы сталкиваемся с математикой – вкусной и красивой математикой! 

В какой обстановке приятнее поглощать пищу? Когда она красиво подана! «Вот это стол – за ним едят!» - писал С. Маршак в своей пьесе «Кошкин дом». Стол – это горизонтальная плоскость. Начинаем с формы стола: это геометрическая фигура: круг, овал, прямоугольник, квадрат. Говоря о форме квадрата в кулинарии, в первую очередь вспоминаем про салфетки - непременный предмет сервировки стола. Салфетки для банкета складываются в форме конверта, трубочки, конуса, паруса, веера, тюльпана и т.д. (и вновь геометрические формы: треугольники, цилиндры, конусы). Столовые приборы (тарелки) тоже имеют свои геометрические формы – форму цилиндра, конуса или усеченного конуса. 

Мясная и овощная нарезки – прямоугольники, треугольники, круги, овалы, конусы из рыбной нарезки и многие другие формы.

Когда       видишь         красиво

оформленный стол, о математике забываешь. А если внимательно присмотреться, то взору откроются фигуры планиметрии и стереометрии!

О чем мечтает почти каждая женщина в мире? О том, как хорошо выглядеть! Иметь стройную фигуру и при этом не ограничивать себя в питании. Возможно ли это? А почему бы и нет. Но поможет нам в этом опять математика. У каждого человека свой жизненный ритм, следуя которому он выполняет различные функциональные обязанности и, конечно же, питается. 

Если научиться питаться правильно – учитывая при приготовлении различных блюд калорийность продуктов, то можно повести борьбу с весом. Сейчас по вопросу составления правильного меню выпускается большое количество литературы, главное – подобрать свое меню и тогда результат не заставит себя долго ждать.

При подсчете калорийности готовых блюд учитываются её изменения при различных видах кулинарной обработки: варка, жарка, тушение, кипячение и др. Учитывается в обязательном порядке потеря белков, жиров, углеводов, витаминов и минералов при обработке и даже при нарезке продуктов. Учитывается потеря массы готового блюда и использование воды при приготовлении. Истинный повар должен обладать хорошей памятью, уметь быстро считать, и знать основные математические понятия: пропорция, проценты, уравнение.