Симметрия в окружающем мире

Муниципальное автономное общеобразовательное учреждение

Средняя общеобразовательная школа №10

 

 

 

 

 

 

 

Исследовательская  работа

 

Симметрия  в окружающем мире

 

 

Выполнил:

                                Ученик 8а класса

                                 Антипин Андрей

 

Руководитель :

                      Игошева А.А.

 

 

Ревда    2021

 

 

Содержание

Введение                                                                                        3

1.Симметрия и виды симметрии                                                   5

1.1       Симметрия                                                                          5

1.2         Виды симметрии                                                                 7

1.2.1. Осевая симметрия                                                            7

       1.2.2  Центральная симметрия                                               8                                                                                              

1.2.1      Трансляционная симметрия                                         10                                                     

1.2.2      Зеркальная симметрия                                                  13                                        

      2 Симметрия в жизни                                                                  15

   2.1   Симметрия в живой природе                                             15

   2.1.1 Симметрия в растениях                                                     16

2.1.2 Симметрия в мире насекомых, рыб, птиц, животных и человека 18

2.2 Симметрия в неживой природе                                             22

2.3 Симметрия в архитектуре                                                      23

2. 4. Симметрия в технике                                                             25

2.5. Симметрия в быту                                                                  26

2.6. Симметрия в шахматах                                                          27

Заключение                                                                                   34

Список использованных источников                                         35

 

 

                                                              

 

 

Введение

        Понятие симметрии проходит через всю многовековую историю человеческого творчества. Симметрия встречается часто и  повсеместно - в природе, технике, искусстве, науке. Например, если сверху посмотреть на любое насекомое и мысленно провести посередине прямую (плоскость), то левые и правые половинки насекомых будут одинаковыми и по расположению, и по размерам, и по окраске. Ведь мы ни разу не видели, чтобы у жука или стрекозы, у любого другого насекомого лапы слева были бы ближе к голове, чем справа, а правое крыло бабочки или божьей коровки было бы больше, чем левое. Такого в природе не бывает, иначе бы насекомые не смогли бы летать.  Свойство симметричности, присущее живой природе, человек использовал в своих достижениях: изобрел самолет, создал уникальные здания архитектуры. Да и сам человек является фигурой симметричной. Также симметрия прочно вошла в математику в результате наблюдения человека за окружающим миром. Оно встречается уже у истоков человеческого знания, его широко используют все без исключения направления современной науки. Принципы симметрии играют важную роль в физике и математике, химии и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке. Законы природы, управляющие неисчерпаемой в своём многообразии картиной явлений, в свою очередь, подчиняются принципам симметрии.

      Актуальность темы.  

             Тема моей работы «Симметрия в окружающем мире »  актуальна и интересна. В наше время, наверное, трудно найти человека, который не имел бы какого-либо представления о симметрии. Мир, в котором мы живем, наполнен симметрией домов и улиц, гор и полей, творениями природы и человека.

Объект исследования – симметрия.

Предмет исследования – симметрия в окружающем мире, симметрия в шахматах.

Цель работы: изучить, как проявляется симметрия в окружающем мире и в шахматах.

Для достижения поставленной цели необходимо выполнить следующие задачи:
Дать общее понятие о симметрии, о видах симметрии, симметрии в  окружающем мире, симметрии в шахматах.

        1. Выбрать из информационных источников и проанализировать симметричность.

        2.    Представить результаты наблюдения в презентации.

Гипотеза исследования: симметрия это - гармония и красота, равновесие, устойчивость.

Методы исследования:

1.     Анализ информации о симметрии в окружающем мире и симметрии в шахматах.

2.     Компьютерное моделирование (обработка фотографий). Обобщение и систематизация полученных данных.

Этапы работы:

1.     Подготовительный. Изучение литературы, составление плана.

2.     Основной. Сбор и обработка информации.

3.     Заключительный. Систематизация полученной информации, составление презентации.

 

 

 

 

 

 

 

 

 

 

1        Симметрия. Виды симметрии

1.1 Симметрия

          По преданию, термин «симметрия» придумал скульптор Пифагор Регийский, живший в г.Регул. Отклонение от симметрии он определил термином «асимметрия».

      Древние греки полагали, что Вселенная симметрична просто потому, что она прекрасна. Считая сферу наиболее симметричной и совершенной формой, они делали вывод о сферичности Земли.

      Представители первой научной школы в истории человечества, последователи Пифагора Самосского, пытались связать симметрию с числом.

       Познавательную силу симметрии оценили философы Древней Греции, используя ее в своих натурфилософских теориях. Так, например, Анаксимандр из Милета, живший в первой половине VI в. до н. э., использовал симметрию в своей космологической теории, где в центре мира поместил Землю — главное, по его мнению, тело мира. Она должна была иметь совершенную, симметричную форму, форму цилиндра. Земля расположена точно в центре, и здесь симметрия имеет смысл равновесия.

              Правилом симметрии пользовались еще скульпторы Древней Греции. Примером может служить композиция западного фронтона храма Зевса и Олимпии. В основу ее положена борьба лапифов (греков) с кентаврами в присутствии бога Аполлона.

         Весы известны человеку с III в. до н. э. В состоянии равновесия массы грузов на разных концах коромысла одинаковы — положение коромысла симметрично относительно центра тяжести.       Симметрия — это не только равновесие, но и покой: стоит добавить на одну из чашек весов дополнительный груз, как они придут в движение. Нарушено равновесие, исчезла симметрия — появилось движение.

            В науку симметрия вошла в 30-х гг. XIX в. в связи с открытием Гесселем 32 кристаллографических классов и появлением теории групп как области чистой математики. Кристаллы наделены наибольшей величиной симметрии из всех реальных объектов. Симметричной в кристаллографии считается фигура, которая делится без остатка на равные и одинаково расположенные части.

        Законы природы являются симметричными, но при ближайшем их рассмотрении, в каждом из них можно найти хоть небольшой изъян. Оказывается, что природа не терпит точной симметрии. Природа почти, но не абсолютно симметрична. Примером этому являются догадки Пифагора, который считал, что орбиты, по которым движутся планеты, являются совершенными окружностями, на самом же деле это не так. Или если мы посмотрим на человека – внешне он симметричен, но строение органов и их расположение абсолютно ассиметрично.

       У древних народов Атлантиды, как стало известно учёным по найденным рукописям термин «симметрия» означал совершенство, а по найденным фигуркам, статуэткам и другим вещам, стало ясно, что в древней Атлантиде было всё строго симметрично.

      В широком смысле симметрию можно понимать как неизменность при каких-либо преобразованиях. Двусторонняя симметрия означает, что правая и левая сторона относительно какой-либо плоскости выглядят одинаково.

     К слову «симметрия» мы привыкаем с детства, и кажется, что в этом ясном понятии ничего загадочного быть не может. Если стать в центре здания и слева от вас окажется то же количество этажей, колонн, окон, что и справа, значит здание симметрично. Если бы можно было перегнуть его по центральной оси, то обе половинки дома совпали бы при наложении. Такая симметрия получила название зеркальной. Этот вид симметрии весьма популярен в животном царстве, сам человек скроен по ее канонам. Законам симметрии подчиняются все формы на свете.

 

 

 

 

 

 

 

  

       1.2 Виды симметрии

         Симметрия делится на два типа симметрии.

         Первый тип – это та симметрия, которую можно непосредственно видеть. Она может быть названа геометрической симметрией.

         Второй тип – эта та симметрия, которая лежит в законах природы и физических явлениях. Ее можно назвать физической симметрией.

         Двусторонняя симметрия означает, что правая и левая сторона относительно какой-либо плоскости выглядят одинаково.

         Выделяют следующие виды симметрии:

1.2.1 Осевая симметрия

         Понятие осевой симметрии представлено следующим образом: «Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Прямая a называется осью симметрии фигуры». Тогда говорят, что фигура обладает осевой симметрией.

 

 

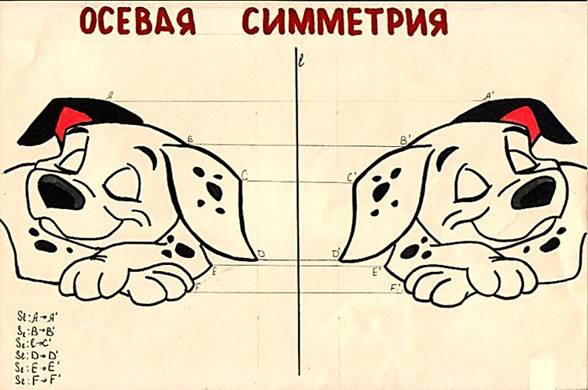
Приведём примеры фигур, обладающих осевой симметрией. У неразвернутого угла одна ось симметрии — прямая, на которой расположена биссектриса угла. Равнобедренный (но не равносторонний) треугольник имеет также одну ось симметрии, а равносторонний треугольник— три оси симметрии. Прямоугольник и ромб, не являющиеся квадратами, имеют по две оси симметрии, а квадрат— четыре оси симметрии. У окружности их бесконечно много — любая прямая, проходящая через её центр, является осью симметрии.

Имеются фигуры, у которых нет ни одной оси симметрии. К таким фигурам относятся параллелограмм, отличный от прямоугольника, разносторонний треугольник.

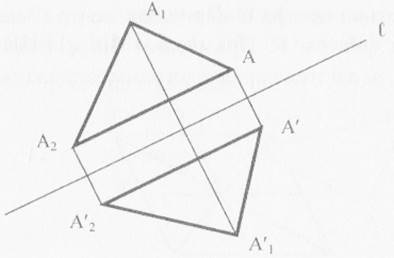
        Преобразование, при котором каждая точка A фигуры (или тела) преобразуется в симметричную ей относительно некоторой оси l точу А, при этом отрезок AA´ l , называется осевой симметрией.

 

 

1.2.2 Центральная симметрия

     Геометрической фигуры, когда любой точке, расположенной по одну сторону центра симметрии, соответствует другая точка, расположенная по другую сторону центра. При этом точки находятся на отрезке прямой, проходящей через центр, делящий отрезок пополам.

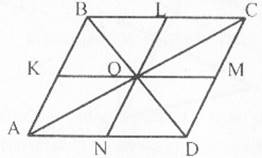
    Примерами фигур, обладающих центральной симметрией, являются окружность и параллелограмм.

        Центром симметрии окружности является центр окружности, а центром симметрии параллелограмма – точка пересечения его диагоналей. Любая прямая также обладает центральной симметрией. Однако, в отличие от является произвольный треугольник. окружности и параллелограмма, которые имеют только один центр симметрии, у прямой их бесконечно много – любая точка прямой является её центром симметрии.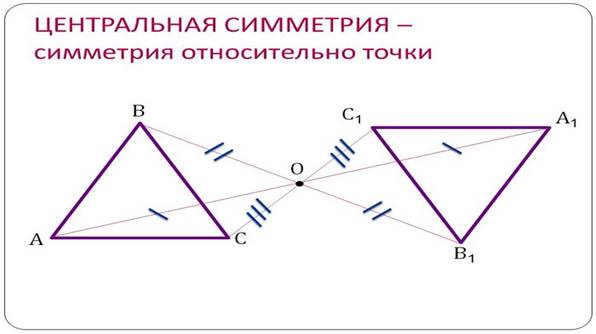

Преобразования, переводящее каждую точку A фигуры или тела в точку A´, симметричную ей относительно центра O, называется преобразованием центральной симметрии или просто центральной симметрией.

 

     Точка O называется центром симметрии и является неподвижной. Других неподвижных точек это преобразование не имеет. Если при преобразовании центральной симметрии относительно центра О фигура F преобразуется в себя, то она называется симметричной относительно центра O.при этом центр O называется центром симметрии фигуры F. Примерами фигур, обладающих центром симметрии, являются параллелограмм, окружность и т.д.

 

1.2.3Трансляционная симметрия

Поворот

                       Преобразование, при котором каждая точка A фигуры или тела поворачивается на один и тот же угол α вокруг заданного центра O, называется вращением или поворотом плоскости. Точка О называется центром вращения, а угол α – углом вращения. Точка O является неподвижной точкой этого преобразования.

 

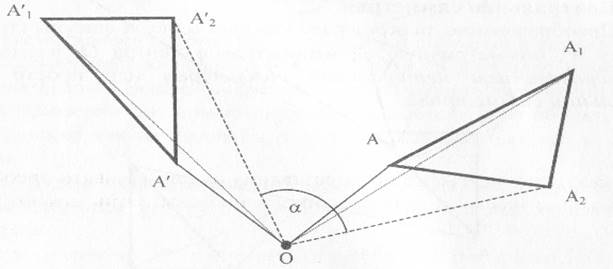
Центральная симметрия есть поворот фигуры или тела на 180˚.

 

Параллельный перенос.

  Преобразование при котором каждая точка фигуры или тела перемещается в одном и том же направлении на одно и то же расстояние, называется параллельным переносом.

Чтобы задать преобразование параллельного переноса, достаточно задать вектор .

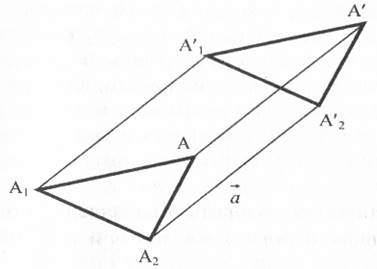
Скользящая симметрия

Скользящей симметрией называется такое преобразование, при котором последовательно выполняются осевая симметрия и параллельный перенос.

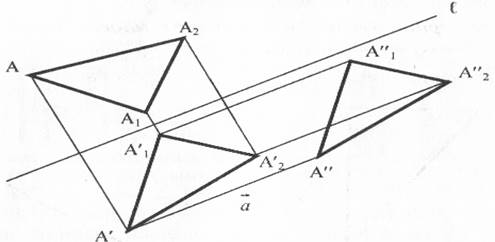
      Все перечисленные преобразования будем называть преобразованиями симметрии. Для преобразований симметрии имеют место следующие свойства:

1.     отрезок переходит в равный ему отрезок;

2.     угол переходит в равный ему угол;

3.     окружность переходит в равную ей окружность;

4.     любой многоугольник переходит в равный ему многоугольник и т.д.;

5.     параллельные прямые переходят в параллельные, перпендикулярные в перпендикулярные.

Симметрия относительно плоскости

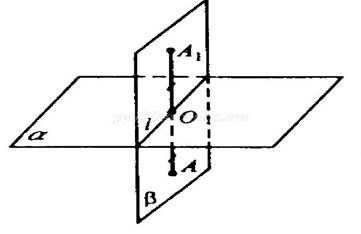
          Рассмотрим произвольную плоскость α в пространстве и такое отображение пространства на себя, при котором каждая точка этой плоскости остается на месте, а точка M, не принадлежащая α переходит в такую точку M´, что плоскость α перпендикулярна отрезку MM´ и проходит через его середину. Это отображение называется симметрией пространства относительно плоскости α.

Математически верное определение

                          Пусть α - произвольная фиксированная плоскость. Из точки X фигуры опускаем перпендикуляр XA на плоскость α и на его продолжении за точку A откладываем отрезок AX´, равный XA. Точка X´ называется симметричной точке X относительно плоскости α, а преобразование, которое переводит точку X в симметричную ей точку X´, называется преобразованием симметрии относительно плоскости α.

                         Если точка X лежит в плоскости α, то считается, что точка X переходит в себя. Если преобразование симметрии относительно плоскости переводит фигуру в себя, то фигура называется симметричной относительно плоскости, а данная плоскость называется плоскостью симметрии этой фигуры.

1.2.4 Зеркальная симметрия

       Хорошо знакома каждому человеку из повседневного наблюдения. Как показывает само название, зеркальная симметрия связывает любой предмет и его отражение в плоском зеркале.

 

   

вложены или наложены друг на друга. Так перчатку правой руки нельзя надеть на левую руку. Симметрично зеркальные фигуры при всём своём сходстве существенно отличаются друг от друга. Чтобы убедиться в этом, достаточно поднести лист бумаги к зеркалу и попытаться прочесть несколько слов, напечатанных на ней, буквы и слова просто-напросто будут перевёрнуты справа налево. По этой причине симметричные предметы нельзя называть равными, поэтому их называют зеркально равными.

Две зеркально симметричные плоские фигуры всегда можно наложить
друг на друга. Однако для этого необходимо вывести одну из них (или обе) из их общей плоскости.

 

     Вообще зеркально равными телами (или фигурами) называются тела (или фигуры) в том случае, если при надлежащем их смещении они могут образовать две половины зеркально симметричного тела (или фигуры).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2   Симметрия в жизни

 

 

2.1   Симметрия в живой природе

 

    Симметрия в природе – это мир вокруг нас. Наука, изучающая её, называется биосимметрией. Симметрией обладают объекты и явления живой природы. Она позволяет живым организмам лучше приспособиться к среде обитания, защитить себя от недоброжелателей и просто выжить.

       В XIX в. появились первые труды, посвященные симметрии растений (французские ученые О.П. Декандоль, О. Браве), животных (немецкий ученый Э. Геккель), биогенных молекул (французские ученые А. Бешан, JL Пастер и др.). В XX в. биообъекты изучались с позиций общей теории симметрии (советские ученые Г.В. Вульф, В.А. Беклемишев, Б.К. Вайнштейн, голландский физхимик Ф.М. Егер, английские кристаллографы во главе с Дж. Берналом), и учения о правизне и левизне (советские ученые В.И. Вернадский, В.В. Алпатов, Г.Ф. Гаузе и др.; немецкий ученый В. Людвиг). К решению проблемы симметрии обращались ученые разных стран: Егер «Лекции о принципе симметрии и его приложениях к естествознанию», Николь «Симметрия и ее приложения», Д Арси Томсон «О росте и форме», Хембидж «Динамическая симметрия» и т.д.

2.1.1 Симметрия в растениях

      Внимательное наблюдение обнаруживает, что основу красоты многих форм, созданных природой, составляет симметрия, точнее все ее виды – от простейших до самых сложных .

       Растительный мир ,  ярко выражен центральной, зеркальной и поворотной симметрией, и другими симметриями, которыми обладают  листья, ветви, цветы, плоды. Изображения на плоскости многих предметов окружающего нас мира имеют ось симметрии или центр симметрии. Многие листья деревьев и лепестки цветов симметричны относительно среднего стебля.

      Среди цветов наблюдаются поворотные симметрии разных порядков. Многие цветы обладают характерным свойством: цветок можно повернуть так, что каждый лепесток займёт положение соседнего, цветок же совместится с самим собой. Такой цветок обладает осью симметрии. Минимальный угол, на который нужно повернуть цветок вокруг оси симметрии, чтобы он совместился с самим собой, называется элементарным углом поворота оси. Этот угол для различных цветов не одинаков. Для ириса он равен 120градусов, для колокольчика – 72градуса, для нарцисса – 60градусов,  . Поворотную ось можно характеризовать и с помощью другой величины, называемой порядком оси и показывающей, сколько раз произойдет совмещение при повороте на 360градусов . Те же цветы ириса, колокольчика и нарцисса обладают осями третьего, пятого и шестого порядков соответственно. Особенно часто среди цветов встречается симметрия пятого порядка. Это такие полевые цветы как колокольчик, незабудка, зверобой, лапчатка гусиная и др.; цветы плодовых деревьев – вишня, яблоня, груша, мандарин и др., цветы плодово-ягодных растений – земляника, ежевика, малина, шиповник; садовые цветы – настурция, флокс и др.

 

 

2.1.2 Симметрия в мире насекомых, рыб, птиц, животных и человека

         Симметрия встречается и в животном мире.      Внимательное наблюдение обнаруживает, что основу красоты многих форм, созданных природой, составляет симметрия, точнее, все её виды – от простейших до самых сложных. Симметрия в строение животных – почти общее явление, хотя почти всегда встречаются исключения из общего правила.

     Под симметрией у животных понимают соответствие в размерах, форме и очертаниях, а также относительное расположение частей тела, находящихся на противоположных сторонах разделяющей линии.

 

 

 

 

 

 

 

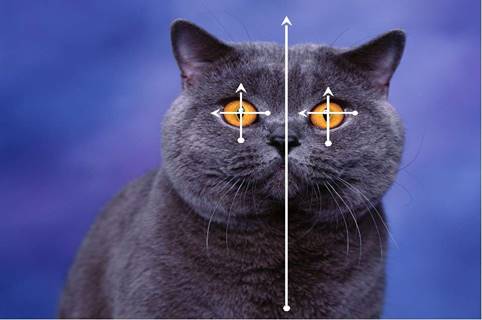
              Рассмотрим, как связаны животный мир и симметрия.

             Как мы знаем, на плоскости существует два вида симметрии: осевая и центральная. Исследование заключается в поиске примеров этих двух видов симметрии в животном мире. Начнём с осевой симметрии.

    Все без исключения удивляются, разглядывая бабочек. Какие лаборатории есть у природы, что она творит такие чудеса?! Если бабочка сложит свои крылья, то они совпадут, так как крылышки у неё одинаковые. Но одинаковость эта не проста! Если на тельце бабочки провести вертикальную среднюю линию и поставить вдоль этой прямой линии зеркало, то одна половинка бабочки спрячется за зеркало. Зато другая - отразится в нём и перед нами опять появится такая же бабочка. Поэтому говорят, что это насекомое зеркально симметрично.

Если мы нарисуем бабочку на листе бумаги, то особую роль для этой плоской фигуры будет играть вертикальная прямая, проходящая посередине её туловища.

       По обе стороны от этой прямой на одинаковом расстоянии от неё находятся одинаковые элементы рисунка. В этом случае говорят, что данная плоская фигура симметрична относительно прямой, а прямую, которая разделяет фигуру на правую и левую половины, называют осью симметрии. В раскраске бабочки можно обнаружить небольшие отклонения. Поэтому говорят, что симметрия бабочки не является математически точной. Зеркальная симметрия характерна для всех представителей животного мира

             Рассмотрим очень интересный вид симметрии – билатеральная.

             Чтобы поднять по эволюционной лестнице приходится самому двигаться быстрее, ловить больше добычи и просто бежать вперёд, чтобы не стать жертвой. Поэтому передняя часть тела начинает отличаться от задней, сдвигаются органы чувств и рот. Остаётся лишь симметрия левой и правой половины. Именно эта симметрия отлично подходит для движения вперёд.

          Люди также являются представителями билатеральной симметрии. Левая и правая половины нашего тела становятся симметричны ещё в состоянии зародыша. За этим стоит сложный механизм, раскрытый Аланом Тьюрингом. Он предположил, что если в живой ткани есть два определённых вещества, которые влияют на производство друг друга, то они могут создавать уникальные узоры.

         Рассмотрим винтовую, или спиральную симметрию. Винтовая симметрия есть симметрия относительно комбинации двух преобразований – поворота и переноса вдоль оси поворота, т.е. перемещение вдоль оси винта и вокруг оси винта. Встречаются левые и правые винты. Примерами природных винтов являются: бивень нарвала – левый винт; раковина улитки – правый винт, но иногда может быть левый винт, шанс того что это случится один на миллион; рога памирского барана – один рог закручен по левой, а другой по правой спирали. Спиральная симметрия не бывает идеальной, например, раковина моллюсков сужается и расширяется на конце.

Человек - существо симметричное

           Не станем пока разбираться, существует ли на самом деле абсолютно симметричный человек. У каждого, разумеется, обнаружится родинка, прядь волос или какая-нибудь другая деталь, нарушающая внешнюю симметрию. Левый глаз никогда не бывает в точности таким, как правый, да и уголки рта находятся на разной высоте, во всяком случае, у большинства людей. И всё же это лишь мелкие несоответствия. Никто не усомнится, что внешне человек построен симметрично: левой руке всегда соответствует правая и обе руки совершенно одинаковы! НО! Здесь стоит остановиться. Если бы наши руки и в самом деле были совершенно одинаковы, мы могли бы в любой момент поменять их. Было бы возможно, скажем, путем трансплантации пересадить левую ладонь на правую руку, или, проще, левая перчатка подходила бы тогда к правой руке, но на самом деле это не так. Каждому известно, что сходство между нашими руками, ушами, глазами и другими частями тела такое же, как между предметом и его отражением в зеркале. Многие художники обращали пристальное внимание на симметрию и пропорции человеческого тела, во всяком случае, до тех пор, пока ими руководило желание в своих произведениях как можно точнее следовать природе.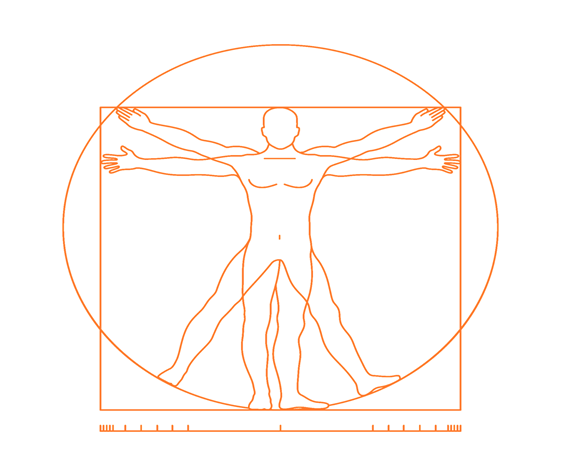

        Известны каноны пропорций, составленные Альбрехтом Дюрером и Леонардо да Винчи. Согласно этим канонам, человеческое тело не только симметрично, но и пропорционально. Леонардо открыл, что тело вписывается в круг и в квадрат. Дюрер занимался поисками единой меры, которая находилась бы в определенном соотношении с длиной туловища или ноги (такой мерой он считал длину руки до локтя). В современных школах живописи в качестве единой меры чаще всего принимается размер головы по вертикали. С известным допущением можно считать, что длина туловища превосходит размер головы в восемь раз. На первый взгляд это кажется странным. Но нельзя забывать, что большинство высоких людей отличаются удлинённым черепом и, наоборот, редко можно встретить низкорослого толстяка с головой удлинённой формы. Размеру головы пропорциональна не только длина туловища, но и размеры других частей тела. По этому принципу построены все люди, оттого-то мы, в общем, похожи друг на друга. Однако наши пропорции согласуются лишь приблизительно, а потому люди лишь похожи, но не одинаковы. Во всяком случае, все мы симметричны!

 

2.2 Симметрия в неживой природе

     Воздействие на облик земной поверхности таких природных факторов, как ветер, вода, солнечный свет, весьма стихийно и часто носит беспорядочный характер. Однако песчаные дюны, галька на морском берегу, кратер потухшего вулкана имеют, как правило, геометрически правильные формы. Именно кристаллы вносят в мир неживой природы очарование симметрии. вопросов

 

      Снежинками учёные заинтересовались сравнительно недавно и совершенно случайно. Они задались вопросом о том, почему они все разные и в то же время симметричные. В итоге выяснилось, что снежинка – это группа кристалликов, образованная более чем из двухсот ледяных частичек. Снежные кристаллы образуются из расположенных в безупречном порядке молекул воды. Каждая снежинка формируется из шестиугольной молекулы воды, поэтому все снежинки шестиугольные. По мнению специалистов, главная особенность, определяющая форму кристалла, - это крепкая связь между молекулами воды, подобная соединению звеньев в цепи. Отсюда и симметрия.                            Симметрия – это свойство кристаллов совмещаться друг с другом в различных положениях путём поворотов, параллельных переносов, отражений.

 

 

2.3 Симметрия в архитектуре

        Человеческое творчество во всех своих проявлениях тяготеет к симметрии. На этот счёт хорошо высказался известный французский архитектор Ле Корбюзье, в своей книге «Архитектура XX века» он писал: «Человеку необходим порядок: без него все его действия теряют согласованность, логическую взаимность. Чем совершеннее порядок, тем спокойнее и увереннее чувствует себя человек. Он делает умозрительные построения, основываясь на порядок, который продиктован ему потребностями его психики, это творческий процесс. Творчество есть акт упорядочения». Нагляднее всего видна симметрия в архитектуре. Особенно блистательно использовали симметрию в архитектурных сооружениях древние зодчие. Использование симметрии в конструкциях зданий, симметричных элементов в отделке, а также симметрично расположенные строения создают красоту и гармонию.  Наиболее распространенный вид симметрии, использующийся при проектировании сооружений, зеркальный. похожа на левую. получившей название ось симметрии.

 

        При рассмотрении симметрии в архитектуре нас будет интересовать геометрическая симметрия – симметрия формы как соразмерность частей целого. Замечено, что при выполнении определенных преобразований над геометрическими фигурами, их части, переместившись в новое положение, вновь будут образовывать первоначальную фигуру. При осевой симметрии части, которые,  взаимно заменяют друг друга, образованы некоторой прямой. Эту прямую принято называть осью симметрии. В пространстве аналогом оси симметрии является плоскость симметрии. Таким образом, в пространстве обычно рассматривается симметрия относительно плоскости симметрии

2. 4Симметрия в технике

      Благодаря симметричности кристаллов симметрия проникла в мир физических законов и стала там полновластной хозяйкой. Вспомним технические объекты - самолеты, мосты, автомашины, ракеты, молотки, гайки - практически все они от мала до велика обладают той или иной симметрией. Случайно ли это? В технике красота, соразмерность механизмов часто бывает связана с их надежностью, устойчивостью в работе. Симметричная форма дирижабля, самолета, подводной лодки, автомобиля и т.д. обеспечивает хорошую обтекаемость воздухом или водой, а значит, и минимальное сопротивление движению. В технике существует своего рода постулат: наиболее целесообразные и функционально совершенные изделия являются наиболее красивыми.

 

 

2.5 Симметрия в быту

       Симметрия встречается в жизни повсюду: в быту, в архитектуре, строительстве. Значит, люди не плохо относятся к ней, раз используют ее в своих целях: для красоты, удобства и изучения, то есть она им нужна и играет в их жизни не последнюю роль.

 

2.6 Симметрия в шахматах

        Симметрия как общий принцип гармонии в молекулах, кристаллах, живой природе имеет глубокий смысл. Изучение ее проявлений и закономерностей играет важную роль в физике, химии, биологии, математике. С помощью симметрии человек веками пытался объяснить или создать порядок, красоту и совершенство. В повседневной жизни мы тоже постоянно сталкиваемся с мотивами симметрии. Господствует симметрия и в шахматных.

       Действительно, разнообразные мотивы симметрии (и асимметрии!) встречаются и на шахматной доске. С одной стороны, речь идет о симметрии естественной, возникающей в самой партии, а с другой - используемой в задачах и этюдах, необычных позициях. Хорошее понимание симметричных структур может стать вашим козырем. Начинающие игроки обычно полагают, что в симметричных позициях, возникающих в разменных вариантах Славянской защиты и Французской защиты, ничья почти гарантирована. Однако подобные положения таят в себе немало яда, так как даже небольшое преимущество позволяет довести партию до победы.

         Всем известен такой забавный случай. Некто явился в шахматный клуб и объявил, что нашел верный способ никогда не проигрывать черными. "Каким образом?" - спросили его. "Очень просто, - ответил гость. - Повторяя ходы противника!" Сыграть с наивным изобретателем вызвался Сэм Лойд, и уже через четыре хода на доске стоял мат. Правда, каким из двух способов - то ли 1. с4 с5 2. Фа4 Фа5 3. Фс6 Фс3 4. Ф:с8x, то ли 1. d4 d5 2. Фd3 Фd6 3. ФB Фh6 4. Ф:с8x - был заматован черный король, история умалчивает.

       Партии, в которых черные повторяют ходы белых, называются обезьяньими. Копирование ходов к добру не приводит, но интересно, как быстро белые могут поставить мат той или иной фигурой, зная о такой принципиальности партнера. Про ферзя мы уже знаем. Для остальных фигур обезьяньи партии с матовым финалом впервые предложил Тракслер еще в начале XIX века. В дальнейшем были установлены абсолютные рекорды.

Ладья: 1. Кf3 Кf6 2. Кg5 Кg4 3. К:h7 К:B 4. К:f8 К:f1 5. Ке6 Ке3 (танец коней закончился) 6. Л:h8x. Конь: 1. Кс3 Кс6 2. Ке4 Ке5 3. е3 е6 4. Ке2 Ке7 5. g3 g6 6. Кf6x. Белопольный слон: 1. е4 е5 2. f4 f5 3. ef ef 4. f6 f3 5. fg fg 6. Се2 Се7 7. СBx. Чернопольный cлон: 1. d4 d5 2. Крd2 Крd7 3. Крd3 Крd6 4. Сe3 Сe6 5. c3 c6 6. Фd2 Фd7 7. Сf4x. Пешка: 1. g4 g5 2. B B 3. Кf3 Кf6 4. Ке5 Ке4 5. hg hg 6. g6 g3 7. g7x. Наконец на девятом ходу матует и сам король: 1. d3 d6 2. Крd2 Крd7 3. Крc3 Крc6 4. Крb3 Крb6 5. Крa3 Крa6 6. Сe3 Сe6 7. Сb6 Сb3 8. ab ab. 9. Крb4x.

       Может сложиться ошибочное впечатление, будто при дублировании ходов черные в лучшем случае добиваются ничьей. Но, как ни странно, аккуратно повторяя ходы партнера, они имеют шанс уже на восьмом ходу... объявить мат белому королю. 1. е4 е5 2. Кре2 Кре7 3. Кре3 Кре6 4. Фf3 Фf6 5. Ке2 Ке7 6. b3 b6 7. Са3 Са6. 8. Кd4+, и у черных нет выбора: 8...еdx!

        Занятно, но белый король матуется и при центрально-симметричной игре черных. 1. e4 d5 2. e5 d4 3. c3 f6 4. ef dc 5. fe cd+ 6. С:d2 С:e7 7. Кf3 Кc6 8. Кc3 Кf6 9. Кe2 Кd7 10. Кfd4 Кce5 11. Кe6 Кd3x!

       Итак, при обезьяньей игре черные могут и сами получить мат, и поставить мат сопернику. В любом случае заматованной оказывается только одна сторона. А вот пат может быть взаимным. В следующей рекордной партии ходы повторяют то черные, то белые, но, главное, в симметричном эпилоге двигаться не в состоянии ни одна из сторон.

1. е4 d5 2. е5 d4 3. c3 f6 4. Фf3 Крf7 5. Ф:b7 Фd5 6. Крd1 Ф:g2 7. Крс2 Ф:f1 8. Ф:с8 Ф:g1 9. Ф:b8 Л:b8 10. Л:g1 Лb3 11. Лg6 Ла3 12. Лh6 gh 13. ba Крg7 14. Крb2 d3 15. e6 a5 16. B a4 17. B c5 18. f4 c4 19. f5, и взаимный пат.

        Если черных обязать точно копировать ходы белых, то пат наступает на три с половиной хода позднее: 1. а4 а5 2. b4 b5 3. ab ab 4. Кc3 Кc6 5. bc bc 6. Лa4 Лa5 7. Лf4 Лf5 8. e4 e5 9. ef ef 10. B B 11. Фg4 Фg5 12. hg hg 13. Кf3 Кf6 14. gf gf 15. Сe2 Сe7 16. fe fe 17. f6 f3 18. d4 d5 19. ЛB Лh6 20. С:h6 С:B 21. gh gh 22. B B. Снова пат и белым и черным.

        Благодаря мотивам симметрии (и асимметрии!) шахматные задачи и этюды приобрета ют дополнительное изящество. Начнем с классической миниатюры.   Разберем, как действовать в симметричных позициях на примере партий, сыгранных опытными гроссмейстерами.

Р. Бианкетти, 1925

Выигрыш

       После вступления 1. Сb2! все фигуры на доске выстроились по большой диагонали. Ладья черных в опасности, и в зависимости от того, куда она двинется, возникают два изящных симметричных варианта.

1...Лf8 (1...Лf7 2. ЛB+ Крg8 3. Лh8x) 2. Лc7+ Крg8 3. Лg7+ Крh8 4. Крa2! (но не 4. Крb1 из-за 4...Лf1+ 5. Крa2 Лa1+ 6. Крb3 Лa3+ 7. Крc2 Лc3+ 8. С:c3 пат), и белые выигрывают ладью. Аналогично 1...Лh6 2. Лg3+ Крh7 3. Лg7+ Крh8 4. Крb1! (4. Крa2 Лa6+ и т. д.) с тем же финалом.

Г. Адамсон, 1924

Выигрыш

       Одна из белых пешек должна двинуться вперед, но какая? 1. B! Крd2 (мало что меняет 1...Крf2) 2. Крd5 Крc2 3. b4 Крb3 4. Крc5 Крc3 5. b5 Крb3 6. Крc6 Крc4 7. Кр:c7, и белый король отправляется в победный марш на королевский фланг. А симметричное вступление - ложный след. 1. b4? Крd2 2. Крd5 Крc3 3. Крc5 g5! 4. B Крb3 5. b5 Крc3 6. Крc6 Крb4 7. Кр:c7 Кр:b5 8. Крd6 Крb6 9. Крe6 Крc6 10. Крf6 Крd7 11. Кр:g5 Крe8 12. Крg6 Крf8, и черные спасаются.

 

 

 

 

Э. Цеплер, 1946

Выигрыш

          А здесь какой пешке стартовать первой? Никакой! После 1. Кре5! белые сохраняют симметрию и ждут, когда черные первыми нарушат ее. Упускает победу как 1. b5? Кd4+ 2. Кр:e7 Крf4 3. b6 Кc6+, так и 1. B Кf4+ 2. Кр:e7 К:B! 3. b5 Кf4 4. Крd6 Кd3 5. b6 Кb4 и 6...Ка6. Обе попытки (симметричные!) с асимметричной игрой не удались. 1...Кf4 (1...Крf3 2. B!) 2. b5 Крf3 3. b6 Крg4 4. B!, 2...Кg6+ 3. Крe6 Крe4 4. b6 Кf4+ 5. Крf7! с победой.

О. Риихимаа, 1942

Ничья

1. de! de (после 1...dc 2. ef Крe7 3. e6 движение черных пешек в конце концов приводит к пату) 2. еf Крe7 3. Крe4 Кр:f7 4. Кр:e5 Крe7 5. Крf5! Крd7 6. Крe5 Крc7 7. Крd4 Крb8 8. Крc4 Крa7 9. Крb4 Крa6 10. Крa4 c ничьей. Но не проходит 1. dc? dc! 2. cb Крc7 3. Крc4 Кр:b7 4. Кр:c5 Крc7 5. Крb5 Крd7 6. Крc5 Крe7 7. Крd4 Крf8 8. Крe4 Крg7 9. Крf4 Крh6!, и черные берут верх благодаря маневру на дальней вертикали "h".

Т. Доусон, 1924  

Выигрыш

       В распоряжении белых два логичных продолжения - 1. Кd4+ (и 2. К:f3) и 1. Кf4+ (и 2. К:d3). Линия "а", которая вносит в позицию асимметрию, как будто не играет никакой роли. То есть если выигрывает шах с d4, то достигает цели и шах с f4. Однако к победе ведет лишь первый из них. 1. Кd4+ Крe3 2. К:f3 Кр:f3 3. Крf8! d2 4. e8Ф d1Ф 5. ФB+, и все кончено. Если черные не ставят ферзя, то эндшпиль "ферзь против центральной пешки" легко выигран. А вот 1. Кf4+ дает только ничью - 1... Крe3 2. К:d3 Кр:d3 3. Крd8 f2 4. e8Ф Крd2! Разница в том, что эндшпиль "ферзь против слоновой пешки" уже ничейный (ситуация, когда белый король стоит близко к этой пешке, не в счет): 5. Фb5 Крe1 6. Фb1+ Крe2 7. Фe4+ Крf1 8. Крe7 Крg1 9. Фg4+ КрB 10. Фf3+ Крg1 11. Фg3+ КрB! 12. Ф:f2 пат.

Смешно, но если линию "а" отрезать от доски, то выигрыша нет ни в одном случае, так как пешка "d" из ферзевой превращается в слоновую.

Рассмотрим  ряд увлекательных задач.

Ф. Хоффман, 1902

Мат в 3 хода

     Классическая миниатюра, которая лет сорок назад была пробным камнем для компьютеров. Три белые пешки на пороге своего превращения в ферзя, но ни одна из них ферзем не станет! 1. е8С! Кр:d6 2. c8Л! Крe6 3. Лc6x или 1...Кр:f6 2. g8Л! Крe6 3. Лg6x.

Теперь две задачи-квартета, в которых фигуры сосредоточились на одной вертикали.

Р. Лермэ, 1923

Мат в 2 хода

     После 1. Фd5! возникают два симметричных эхо-мата: 1...Крe8 (Сg4, Сf3) 2. Фg8x; 1... Крс8 (Са4, Сb3) 2. Фа8x. Но не годится 1. Фg2 - 1...Сg4 или 1. Фа2 - 1...Са4!

Р. Гарро, 1923

Мат в 3 хода

  А здесь ферзь должен покинуть вертикаль. 1. Фа1! Кре8 (с8) 2. Фg7 (а7), и мат следующим ходом. Защищать конем ферзевый фланг - 1...Кb6 бесполезно из-за 2. Фh8x. Не проходит симметричное 1. Фg1? Кf6!, и у белого ферзя слева нет поля, аналогичного h8.

 

 

 

Д. Брейер, 1928

Мат в 4 хода

     Какова роль вертикалей "а", "b" и "с", нарушающих симметрию? Поразительно, но именно на них разворачиваются события. 1. Са7! Справа аналогичное поле отсутствует. 1...f6 2. Кb6! Временно перекрывая слона. 2...Кре3 3. Кс4+ Крf3 4. Кd2x. Эффектная "индийская тема", выраженная в симметричной форме.

Б. Линдгрен, 1981

Мат в 2 хода

1. Ка3! Грозит 2. К:b5x, и, куда бы ни отступила ладья, черным несдобровать: 2. Фc5x или 2. Фb4x. Не проходит 1. Кс7 (1. Кс3)? из-за 1...Ла5! и собственные кони мешают белым объявить мат. Но почему не 1. Кg3 c симметричной угрозой 2. К:f5x? Оказывается, черных спасает 1...СB! - вот линия "h" и пригодилась.

    Проанализировав   партии, шахматные задачи  можно сделать вывод, что  зеркальное отражение доски дает симметричную позицию. Выходит, из любой шахматной задачи можно получить другую, симметричную. Но существует ход, который не сохраняется при отражении, - рокировка.

 

 

 

 

 

 

 

 

 

 

 

 

 

Заключение

        При сборе материала для выполнения работы я узнал много нового и научился применять приобретенные геометрические знания для описания и анализа закономерностей, существующих в окружающем мире . Еще я получил возможность ознакомиться с научно-популярной литературой по проблеме взаимосвязи симметрии в  архитектуре, в шахматах и провел поиск информации, необходимой для подтверждения или опровержения фактов, и проанализировал шахматные позиции  и  вывод, что зеркальное отражение доски дает симметричную позицию, считается верным, что в шахматах наблюдается симметрия .Исследования, проведенные мной, показали, что симметрия обнаруживается и в жизни, и в   архитектуре, и в природе, и в шахматах, является одним из принципов гармоничного построения мира. «Сфера влияния» симметрии поистине безгранична. Всюду она определяет гармонию природы, мудрость науки и красоту искусства. Цель поставленная в работе -достигнута.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Список использованных источников

1. Гильде В.  Зеркальный мир. — М.: Мир, 1982г.

2.  Заренков Н. А.  Биосимметрика М.: Книжный дом «ЛИБРОКОМ», 2009. — 320 с.

3.Тарасов Л. В. Этот удивительный симметричный мир. –М.: Просвещение, 1982.

4.  Шафрановский И. И. Симметрия в природе. Ленинград, «Недра», 1985. — 168 с.

5 Наука и жизнь, МНОГОЛИКАЯ СИММЕТРИЯ  https://www.nkj.ru/archive/articles/4504

6.Heads, Michael. «Principia Botanica: Croizat’s Contribution to Botany.» Tuatara 27.1 (1984): 26-48. (англ.)

Интернет-ресурсы 7. http://www.limm.mgimo.ru/science/ 8. www.numanities.edu.ru 9. www.nrc.edu.ru 10. www.toe-krsh.narod.ru 11. http://boltai.com/g/nauka/

 

 

 

 

 

 

 

 

 

 

 

Скачано с www.znanio.ru