Симметрия и золотое сечение в архитектуре города Кемь

Муниципальное бюджетное общеобразовательное учреждение «Подужемская средняя общеобразовательная школа»

  Кемского муниципального района

 

 

 

 

 

 

Симметрия и золотое сечение

 в архитектуре города Кемь

 

 

 

Проектно-исследовательская  работа

 

 

 

 

 

                                                                           Выполнили:

учащиеся 6 класса

Агаев Анар

Колобова София

Иванова Анастасия

Юрченко Яна

                                                                              

Руководитель:

Гладышева Е.Н.

учитель математики                                                                               

 

 

 

 

 

 

 

Кемь - 2014

 

 

          Содержание.

 

I. Паспорт проекта……………………………………………………………...3

II. Аннотация проекта    ………… …………………………………………….4

III. План проекта    ………………………………………………………...........5

IV. Теоретическая часть

1. Введение  ………………………………………………………………....6
2. Определение симметрии и виды симметрии …………………………..7
3. Архитектура и стили архитектуры    ……………………………………11

VI.Заключение……………………………………………………………. …….14

VII. Исследовательская часть

Некоторые примеры взаимосвязи математики и архитектуры.........................15

VIII. Приложения (1 – 7)………………………………………………………...16

IX. Список использованной литературы……………………………………………………………………….20

 

 

 

 

 

 

I.       Паспорт проекта        

 

Название	Симметрия и золотое сечение в архитектуре города Кемь
Руководитель	Гладышева Елена Николаевна
Консультант	Кулишова Наталия Ивановна , учитель истории
Тип	Исследовательский практико-ориентированный монопроект
Основная учебная дисциплина	Геометрия
Дополнительные дисциплины	Искусство, краеведение
Цель	Выявить, насколько широко симметрия и золотое сечение присутствует в архитектурных сооружениях
Задачи	Определить, что называют симметрией, что называют золотым сечением, рассмотреть некоторые виды симметрии, определить, что называют архитектурой, рассмотреть стили архитектуры, исследовать архитектурные сооружения города Кемь, при проектировании которых использовалась симметрия и золотое сечение.
Проблема	·         Существование гармонии в окружающем нас мире. ·         Применение знаний о золотом сечении и симметрии  в исследовании объектов города Кемь.
Предполагаемый результат	Выявление симметрии и золотого сечения в архитектурных сооружениях
Предполагаемый продукт	Презентация
Необходимое оборудование	Материально-техническая база эксперимента – книги, компьютер

 

 

 

 

 

 

 

 

II.Аннотация проекта

 

Данный проект предназначен для выявления того, насколько широко симметрия и золотое сечение используется в архитектурных сооружениях.

 

Цель: выявить, насколько широко симметрия и золотое сечение присутствует в архитектурных сооружениях

Всё это в процессе работы определило приоритетность решаемых задач:

• Определить, что называют золотым сечением.
• Определить, что называют симметрией.
• Рассмотреть некоторые виды симметрии.
• Определить, что называют архитектурой.
• Рассмотреть стили архитектуры.
• Исследовать некоторые архитектурные сооружения города Кемь, при проектировании которых использовалась симметрия и золотое сечение.

 

Гипотеза – симметрия и золотое сечение часто присутствует в архитектурных сооружениях

Предмет исследования – архитектура, симметрия, золотое сечение.

Объект исследования – архитектурные сооружения города Кемь

В процессе работы формируются навыки сравнительно-сопоставительного анализа, возникает представление о симметрии и золотом сечении,  развивается творческое воображение.

 

 

 

 

 

 

 

 

 

 

 

 

                                     III. План проекта

 

№	Этап	Направление работы	Сроки	Планируемый результат
1	Подготовительный	Выбор проблемы, источников литературы, составление плана	Декабрь 2013	Определение поля деятельности и структуры работы.
2	Деятельностный	Формулирование гипотезы, проведение опытно-экспериментальной работы.	Январь- февраль 2014	Научное обоснование темы заявленного проекта и глубины освещения исследуемого вопроса.
3	Ход исследования	Работа с литературой и другими источниками	Март- май  2014	Подготовка теоретических выкладок и материала.
4	Рефлексивный	Обработка полученных данных	Сентябрь- октябрь 2014	Окончательное определение содержательной и практической составляющих проекта
5	Аналитический	Анализ результатов, формулирование выводов	Октябрь- ноябрь 2014	Формулировка заключения и практических выкладок по проекту
6	Презентационный	Мультимедийная подготовка	Декабрь 2014

 

 IV. Теоретическая часть

Геометрия владеет двумя сокровищами:
         одно из них – теорема Пифагора,
         другое- деление отрезка в среднем
       и крайнем отношении.
                                         И. Кеплер

1.      Введение.

Есть вещи, которые нельзя объяснить. Вот вы подходите к пустой скамейке и садитесь на нее. Где вы сядете — посередине? Или, может быть, с самого края? Нет, скорее всего, не то и не другое. Вы сядете так, что отношение одной части скамейки к другой, относительно вашего тела, будет равно примерно 1,62. Простая вещь, абсолютно инстинктивная... Садясь на скамейку, вы произвели «золотое сечение». О золотом сечении знали еще в древнем Египте и Вавилоне, в Индии и Китае. Великий Пифагор создал тайную школу, где изучалась мистическая суть «золотого сечения». Евклид применил его, создавая свою геометрию, а Фидий — свои бессмертные скульптуры. Платон рассказывал, что Вселенная устроена согласно «золотому сечению». А Аристотель нашел соответствие «золотого сечения» этическому закону. Высшую гармонию «золотого сечения» будут проповедовать Леонардо да Винчи и Микеланджело, ведь красота и «золотое сечение» — это одно и то же. А христианские мистики будут рисовать на стенах своих монастырей пентаграммы «золотого сечения», спасаясь от Дьявола. При этом ученые — от Пачоли до Эйнштейна — будут искать, но так и не найдут его точного значения. Бесконечный ряд после запятой — 1,6180339887... Странная, загадочная, необъяснимая вещь: эта божественная пропорция мистическим образом сопутствует всему живому. Неживая природа не знает, что такое «золотое сечение». Но вы непременно увидите эту пропорцию и в изгибах морских раковин, и в форме цветов, и в облике жуков, и в красивом человеческом теле. Все живое и все красивое — все подчиняется божественному закону, имя которому — «золотое сечение». Так что же такое «золотое сечение»?.. Что это за идеальное, божественное сочетание? Может быть, это закон красоты? Или все-таки он — мистическая тайна? Научный феномен или этический принцип? Ответ неизвестен до сих пор. Точнее — нет, известен. «Золотое сечение» — это и то, и другое, и третье. Только не по отдельности, а одновременно... И в этом его подлинная загадка, его великая тайна.

2.      Золотое сечение

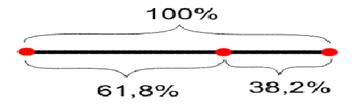
Золотое сечение - деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине.

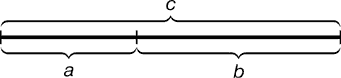
Эта пропорция равна

 

 

 

Золотое сечение в процентах

 

Золотой треугольник

Золотым называется такой равнобедренный треугольник, основание и боковая сторона которого находятся в золотом отношении:  

 

 

 

Золотой прямоугольник

Прямоугольник, стороны которого находятся в золотом отношении, т.е. отношение длины к ширине даёт число φ, называется золотым прямоугольником.

 

3.Определение симметрии и виды симметрии Соня

  

    Если мы заглянем в «Современный словарь иностранных слов», то обнаружим, что под симметрией понимается «соразмерность, полное соответствие в расположении частей целого относительно средней линии, центра... такое расположение точек относительно точки, прямой или плоскости, при котором каждые две соответствующие точки, лежащие на одной прямой, проходящей через центр симметрии, на одном перпендикуляре к оси или плоскости симметрии, находятся от них на одинаковом расстоянии...».

                Рассмотрим симметрию в геометрии

 Две точки, лежащие на одном перпендикуляре к данной или прямой по разные стороны и на одинаковом расстоянии от нее, называются симметричными относительно этой или прямой.

 

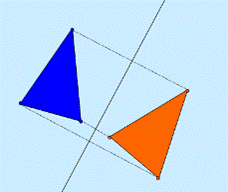
       Фигура симметрична относительно прямой или, если ее точки попарно обладают указанным свойством. Но это только один из видов симметрии, которую изучает математика, так называемая осевая симметрия.

 

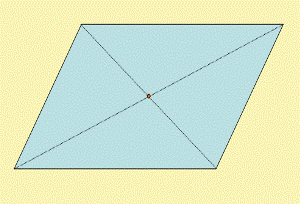
      Фигура симметрична относительно точки, если ее точки попарно лежат на прямых, проходящих через центр симметрии, по разные стороны и на равных расстояниях от него. Этот вид симметрии называется центральной симметрией.

 

     

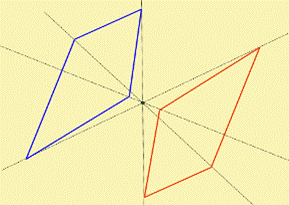
  В пространстве аналогом оси симметрии является плоскость симметрии. Отображение пространства на себя относительно плоскости называют зеркальной симметрией. Название это оправдано тем,  что обе части фигуры, находящиеся по разные стороны от плоскости симметрии, похожи на некоторый объект и его отражение в зеркале.

 

      

       Еще одним видом симметрии является переносная симметрия. Этот вид симметрии состоит в том, что части целой формы организованы таким образом, что каждая следующая повторяет предыдущую и отстоит от нее на определенный интервал в определенном направлении. Этот интервал называют шагом симметрии. Переносная симметрия обычно используется при построении бордюров. В произведениях архитектурного искусства ее можно увидеть в орнаментах или решетках, которые используются для их украшения. Переносная симметрия используются и в интерьерах зданий.

    

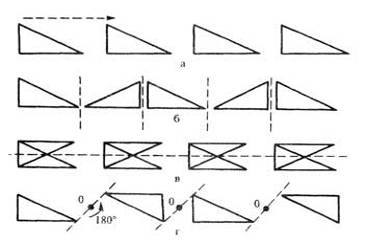
В построении бордюров используются математические принципы.

Для создания бордюров - линейных орнаментов используются следующие преобразования:
а) параллельный перенос;
б) зеркальная симметрия с вертикальной осью;
в) зеркальная симметрия с горизонтальной осью;
г) поворотная (центральная симметрия).

 

        

 

4. Архитектура и стили архитектуры Яна

    Архитектура - это строительное искусство, умение проектировать и создавать города, жилые дома, общественные и производственные здания, площади и улицы, парки. Во многих городах мира можно встретить строения перед которыми захочется остановиться и повнимательнее их рассмотреть. Шедевры архитектуры запоминаются как символы народов и стран. Всему миру известны Кремль и Красная площадь в Москве, Эйфелева башня в Париже, древний Акрополь в Афинах. Архитектура окружает нас и образует пространственную среду для жизни и деятельности людей. Это дома, где мы живём, школы где мы учимся; в садах, парках и дворах - отдыхаем. На заводах и в учреждениях работают наши родители; магазины, вокзал постоянно заполнены посетителями. Трудно даже представить, как можно обойтись без этих и многих других сооружений. В древности задачи архитектуры определяли тремя качествами - пользой, прочностью, красотой. Памятники архитектуры, относящиеся к разным эпохам и странам, отличаются друг от друга по внешнему виду или по стилю, как отличались условия проживания и художественные вкусы людей тех времен.

             В архитектуре, как и в других видах искусства, существует понятие стиля, т.е. исторически сложившейся совокупности художественных средств и приемов.

     В средние века возник готический стиль. Готические здания отличаются обилием ажурных, как кружева, украшений, скульптур, орнаментов. Окна, порталы, своды имеют характерную стрельчатую форму.

     Архитекторы Возрождения создали стиль ренессанс, в котором использовали наследие античного искусства, греческие архитектурные ордеры. Здания в стиле ренессанс были строгими по форме, с четкими прямыми линиями.

     Стиль барокко, пришедший на смену ренессансу, отличается обилием криволинейных форм. Прямые линии почти отсутствуют. Архитектурные формы изгибаются, громоздятся одна на другую и переплетаются со скульптурой.

     Все здания, построенные в стиле классицизма, имеют четкие прямолинейные формы и симметричные композиции. На фоне гладких стен выступают портики и колоннады, которые придают сооружениям торжественную монументальность и парадность. Декоративное убранство из барельефов и статуй оживляют облик зданий.

      Архитектура – удивительная область человеческой деятельности. В ней тесно переплетены и строго уравновешены наука, техника, искусство. Только соразмерное, гармоничное сочетание этих начал делает возводимое человеком  сооружение памятником архитектуры. Из всех видов искусств архитектура, на мой взгляд, ближе всех к математике: в основе конструкций лежат точнейшие расчеты.

 

Заключение.

     В нашей работе мы рассмотрели архитектурные сооружения, построенные в нашем городе, и выявили, что в архитектуре каждого из них просматривается симметрия и золотое сечение.

      Памятники архитектуры буквально пронизаны математикой, численными расчетами и геометрией. 

  Исследования показали, что все виды симметрии используются при проектировании и конструировании архитектурных сооружений и оформлении фасадов зданий, почти в каждом из памятников архитектуры г. Кемь есть золотое сечение.

     Как бы ни развивалось в дальнейшем искусство, элементы симметрии и золотого сечения в нем все же будут преобладать.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

            VII. Исследовательская часть.

 

      Для исследования мы взяли несколько архитектурных сооружений, находящихся в городе Кемь, построенные в разные года  и века.

 

Здание вокзала, знак при въезде в город  

(ПРИЛОЖЕНИЕ 1).

 

Памятники В.И.Ленину, В.А. Минину, С.М.Кирову, памятник где проходили революционные выступления рабочих (пос. Рабочеостровск), мемориал

 (ПРИЛОЖЕНИЕ 2).

 

Успенский собор

 (ПРИЛОЖЕНИЕ 3).

 

Благовещенский собор (ПРИЛОЖЕНИЕ 4).

 

Часовня «Троицы» на территории успенского собора

( ПРИЛОЖЕНИЕ 5).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                         

 VIII. Приложения

ПРИЛОЖЕНИЕ 1.

 

 

 

 

 

 

IX. Список использованной литературы

 

1. Я познаю мир: Детская энциклопедия.Архитектура.1990
2. Л.С.Атанасян Геометрия 7-9, 10-11.Москва «Просвещение» 2005
3. Большая энциклопедия Кирилла и Мефодия. Электронное издание.
4. http ://www.elohovo.narod.ru.
5. http ://www.ru.wikipedia.org.
6. http ://www.hist-singhts.ru
7. http ://www.museum.ru

Скачано с www.znanio.ru