
5.1. Переход от одного опорного плана к другому
Пусть известна К-матрица на S-ом шаге алгоритма решения ЗЛП
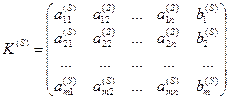 .
(5.1)
.
(5.1)
Обозначим через ![]() вектор номеров базисных
(единичных) столбцов матрицы
вектор номеров базисных
(единичных) столбцов матрицы ![]() ,
, ![]() - вектор, компоненты которого есть
базисные компоненты опорного плана (базисные переменные), определяемого
матрицей
- вектор, компоненты которого есть
базисные компоненты опорного плана (базисные переменные), определяемого
матрицей ![]() , и могут быть отличны от нуля.
Остальные (n - m)
компонент опорного плана, определяемого матрицей
, и могут быть отличны от нуля.
Остальные (n - m)
компонент опорного плана, определяемого матрицей ![]() ,
равны нулю (свободные переменные). Очевидно, что векторы
,
равны нулю (свободные переменные). Очевидно, что векторы ![]() и
и ![]() полностью
задают опорный план, определяемый матрицей
полностью
задают опорный план, определяемый матрицей ![]() .
Например, пусть
.
Например, пусть
![]() =
=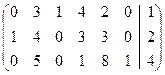 ,
,
тогда ![]() ;
;
![]() и, следовательно, опорный план,
определяемый
и, следовательно, опорный план,
определяемый ![]() , имеет вид
, имеет вид ![]() =(2,0,1,0,0,4).
=(2,0,1,0,0,4).
Итак, пусть К-матрица (5.1) определяет невырожденный опорный план
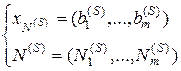 (5.2)
(5.2)
Выберем в матрице ![]() столбец
столбец ![]() , не принадлежащий единичной
подматрице, т.е.
, не принадлежащий единичной
подматрице, т.е. ![]() ,
, ![]() и такой, что в этом столбце есть
хотя бы один элемент больше нуля.
и такой, что в этом столбце есть
хотя бы один элемент больше нуля.
Пусть ![]() . Считая
. Считая ![]() направляющим
элементом, совершим над матрицей
направляющим
элементом, совершим над матрицей ![]() один шаг метода
Жордана-Гаусса. В результате получим новую матрицу
один шаг метода
Жордана-Гаусса. В результате получим новую матрицу
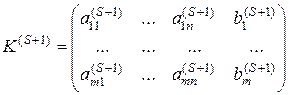 , (5.2)
, (5.2)
в которой
столбец ![]() стал единичным, но которая может и
не быть К-матрицей, так как среди величин
стал единичным, но которая может и
не быть К-матрицей, так как среди величин ![]() могут
быть отрицательные. Условия выбора направляющего (опорного) элемента
могут
быть отрицательные. Условия выбора направляющего (опорного) элемента ![]() , позволяющие получить новую К-матрицу
-
, позволяющие получить новую К-матрицу
- ![]() , т.е. обосновывающие способ
перехода от опорного плана
, т.е. обосновывающие способ
перехода от опорного плана ![]() к опорному
плану
к опорному
плану ![]() , составляет содержание следующей
теоремы:
, составляет содержание следующей
теоремы:
Теорема 5.1 Пусть в k-м столбце К-матрицы
![]() -
- ![]() есть
хотя бы один строго положительный элемент (
есть
хотя бы один строго положительный элемент (![]() ,
,![]() ). Тогда с помощью одного шага
метода Жордана-Гаусса можно построить новую К-матрицу -
). Тогда с помощью одного шага
метода Жордана-Гаусса можно построить новую К-матрицу - ![]() , выбрав направляющий элемент из
условия:
, выбрав направляющий элемент из
условия:
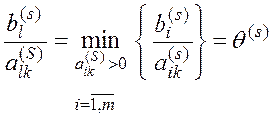 . (5.3)
. (5.3)
Доказательство теоремы следует из следующих соображений. Представим К-матрицу в следующем виде
![]()
![]()
![]()
![]()
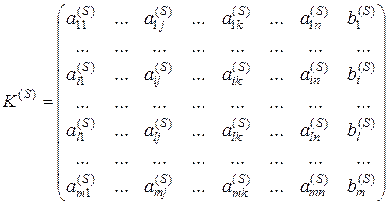 . (5.4)
. (5.4)
Тогда переход к следующей К-матрице (![]() ) с помощью метода Жордана-Гаусса,
полагая элемент
) с помощью метода Жордана-Гаусса,
полагая элемент ![]() направляющим, можно
описать посредством выражений:
направляющим, можно
описать посредством выражений:
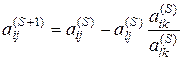 , где
, где ![]() , (5.5)
, (5.5)
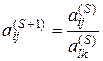 , где
, где ![]() ,
(5.6)
,
(5.6)
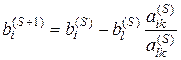 , где
, где ![]() , (5.7)
, (5.7)
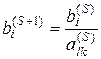 , где
, где ![]() .
(5.8)
.
(5.8)
Итак, если задан k-й столбц К-матрицы
![]() , в котором следует выбрать
направляющий элемент
, в котором следует выбрать
направляющий элемент ![]() так, чтобы полученная в
процессе шага метода Жордана-Гаусса матрица была К-матрицей (т.е.
все её элементы
так, чтобы полученная в
процессе шага метода Жордана-Гаусса матрица была К-матрицей (т.е.
все её элементы ![]() оставались
неотрицательными), то рассматривая (5.7) получим
оставались
неотрицательными), то рассматривая (5.7) получим 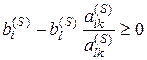 или
иначе
или
иначе 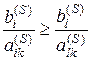 , откуда следует (5.3). Для (5.8)
выражение (5.3) следует автоматически.
, откуда следует (5.3). Для (5.8)
выражение (5.3) следует автоматически.
5.2. Определение симплекс-разности. Способ перехода к лучшему опорному плану. Критерии оптимальности опорного плана и отсутствия конечного решения
Определение 5.1. Величину
![]() ,
(5.4)
,
(5.4)
где ![]() - вектор, компонентами которого
являются коэффициенты целевой функции
- вектор, компонентами которого
являются коэффициенты целевой функции ![]() при
базисных (
при
базисных (![]() ) переменных опорного плана,
определяемого матрицей
) переменных опорного плана,
определяемого матрицей ![]() , назовем j-й симплекс-разностью матрицы
, назовем j-й симплекс-разностью матрицы ![]() .
.
Если столбец ![]() является единичным в
матрице
является единичным в
матрице ![]() , то
, то ![]() =0.
=0.
Пусть ![]() и
и ![]() -
опорные планы, определяемые матрицами
-
опорные планы, определяемые матрицами ![]() и
и
![]() соответственно. Тогда очевидно,
что
соответственно. Тогда очевидно,
что
![]() ;
; ![]() ; (5.5)
; (5.5)
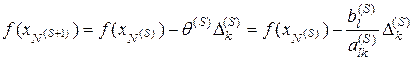 , (5.6)
, (5.6)
где k -
номер столбца ![]() , вводимого в базис при
получении матрицы
, вводимого в базис при
получении матрицы![]() из
из![]() , а
, а ![]() определяется
по формуле (5.3).
определяется
по формуле (5.3).
Выражение (5.6) следует из следующих соображений:
1. Так как в базисном решении на S-ом шаге
переменная ![]() была свободной и соответственно
была свободной и соответственно ![]() , а при введении столбца
, а при введении столбца ![]() в базис на (S+1)-ом
шаге переменная
в базис на (S+1)-ом
шаге переменная ![]() . Таким образом целевая
функция увеличится на величину равную
. Таким образом целевая
функция увеличится на величину равную ![]() .
С другой стороны на основании (5.8)
.
С другой стороны на основании (5.8) 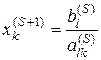 . Откуда
окончательно имеем, что целевая функция возрастёт на величину
. Откуда
окончательно имеем, что целевая функция возрастёт на величину
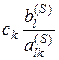 .
(5.7)
.
(5.7)
2. Из рассмотрния (5.7) видно, что значения базисных переменных с
индексами ![]() при переходе с S-го на (S+1)-й шаг
уменьшаются соответственно на величины
при переходе с S-го на (S+1)-й шаг
уменьшаются соответственно на величины 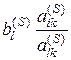 .
Но тогда и целевая функция уменьшиться на сумму вида
.
Но тогда и целевая функция уменьшиться на сумму вида
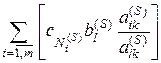 .
(5.8)
.
(5.8)
Объединяя (5.7), (5.8) получим
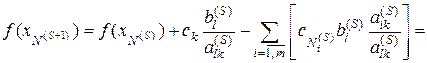
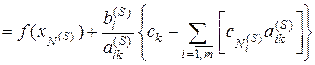 ,
,
откуда с учётом (5.4) непосредственно следует (5.6).
Теорема 5.2. Пусть в матрице ![]() есть
есть
![]() и в столбце
и в столбце ![]() (
(![]() ,
,
![]() ) есть хотя бы один строго
положительный элемент. Тогда от матрицы
) есть хотя бы один строго
положительный элемент. Тогда от матрицы ![]() можно
перейти к матрице
можно
перейти к матрице ![]() , причем
, причем
![]() . (5.9)
. (5.9)
Неравенство (5.9) вытекает из выражения (5.6), так как ![]() , а
, а ![]() .
.
Теорема 5.3. Пусть все симплекс-разности матрицы ![]() неотрицателные. Тогда опорный план
неотрицателные. Тогда опорный план
![]() , определяемый матрицей
, определяемый матрицей ![]() , является оптимальным.
, является оптимальным.
Теорема 5.4. Пусть в матрице ![]() есть
есть
![]() , и в столбце
, и в столбце ![]() (
(![]() ,
,
![]() ) нет ни одного строго
положительного элемента. Тогда ЗЛП, определяемая К-матрицей на S-ом шаге алгоритма, не имеет конечного решения.
) нет ни одного строго
положительного элемента. Тогда ЗЛП, определяемая К-матрицей на S-ом шаге алгоритма, не имеет конечного решения.
5.3. Алгоритм симплекс-метода
Будем считать, что известна исходная К-матрица К(0) ЗЛП, определяющая исходный опорный план:
![]() ,
, ![]() .
.
В симплексном методе последовательно строят К-матрицы К(0),
К(1), …, К(s) задачи
линейного программирования, пока не выполнится критерий оптимальности или
критерий, позволяющий убедиться в отсутствии конечного решения. Рассмотрим
алгоритм S-й итерации симплексного метода. В начале S-й
итерации имеем К-матрицу ![]() задачи
линейного программирования, определяющую опорный план
задачи
линейного программирования, определяющую опорный план
![]() ,
, ![]() .
.
Шаг 1. Вычисляем для столбцов ![]() (
(![]() ,
, ![]() )
матрицы
)
матрицы ![]() симплекс-разности
симплекс-разности ![]() и находим номер k из условия
и находим номер k из условия ![]() .
.
Шаг 2. Если ![]() , то опорный
план
, то опорный
план ![]() ,
, ![]() является
оптимальным, а
является
оптимальным, а ![]() есть оптимальное
значение целевой функции, иначе переходим к шагу 3.
есть оптимальное
значение целевой функции, иначе переходим к шагу 3.
Шаг 3. Если ![]() ,
, ![]() , то ЗЛП не имеет конечного решения,
иначе находим номер l из условия
, то ЗЛП не имеет конечного решения,
иначе находим номер l из условия
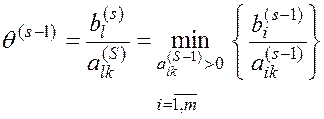
Таким образом, направляющий элемент на S-й итерации метода найден:
![]() .
.
Шаг 4. Вычисляем компоненты вектора ![]() :
:
![]() ,
, ![]() ,
,
![]() .
.
Шаг 5. Производим один шаг метода Жордана-Гаусса с направляющим
элементом ![]() . Присваиваем переменной S
алгоритма следующее значение и переходим к шагу 1.
. Присваиваем переменной S
алгоритма следующее значение и переходим к шагу 1.
5.4. Примеры решения задач симплекс-методом
Пример 5.1. Симплекс-методом решить ЗЛП:
![]() (5.10)
(5.10)
при наличии ограничений:
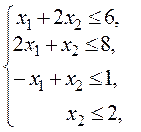 (5.11)
(5.11)
![]() ,
, ![]() .
(5.12)
.
(5.12)
Приводим систему линейных неравенств (5.11) к каноническому виду, вводя
в каждое неравенство дополнительную переменную ![]() ,
,
![]() . Получим систему линейных
уравнений:
. Получим систему линейных
уравнений:
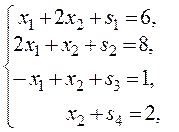 (5.11)
(5.11)
Целевая функция принимает вид
![]() (5.12)
(5.12)
Расширенная матрица 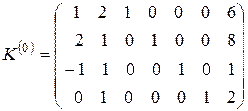
системы линейных уравнений (5.11) является исходной К-матрицей ЗЛП, которая определяет исходный опорный план:
![]() ,
, ![]() .
.
Кроме того, ![]() .
.
Результаты последовательных итераций симплекс-алгоритма удобно оформить в виде симплекс-таблицы (см. табл. 5.1).
Таблица 5.1
|
S |
i |
|
|
|
3 |
2 |
0 |
0 |
0 |
0 |
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|||||
|
|
|
|
|
|
|
|
|||||
|
|
1 2 3 4 |
3 4 5 6 |
0 0 0 0 |
6 8 1 2 |
1 2 -1 0 |
2 1 1 1 |
1 0 0 0 |
0 1 0 0 |
0 0 1 0 |
0 0 0 1 |
6 4 - - |
|
|
|
-3 |
-2 |
0 |
0 |
0 |
0 |
k=1 l=2 |
|||
|
|
1 2 3 4 |
3 1 5 6 |
0 3 0 0 |
2 4 5 2 |
0 1 0 0 |
3/2 1/2 3/2 1 |
1 0 0 0 |
-1/2 1/2 1/2 0 |
0 0 1 0 |
0 0 0 1 |
4/3 8 10/3 2 |
|
|
|
0 |
-1/2 |
0 |
3/2 |
0 |
0 |
k=2 l=1 |
|||
|
2 |
1 2 3 4 |
2 1 5 6 |
2 3 0 0 |
4/3 10/3 3 2/3 |
0 1 0 0 |
1 0 0 0 |
2/3 -1/3 -1 -2/3 |
-1/3 2/3 1 1/3 |
0 0 1 0 |
0 0 0 1 |
|
|
|
|
0 |
0 |
1/3 |
4/3 |
0 |
0 |
|
|||
На второй итерации S = 2,
все ![]() , следовательно, опорный план
, следовательно, опорный план
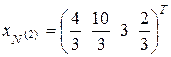 ,
, ![]() ,
,
определяемый К-матрицей К(2), оптимальный. Тогда
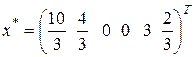 ,
, ![]() .
.
Пример 5.2. Симплекс-методом решить ЗЛП:
![]() (5.13)
(5.13)
при наличии ограничений:
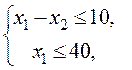 (5.14)
(5.14)
![]() ,
,
![]() .
(5.15)
.
(5.15)
Приводим систему линейных неравенств (5.14) к каноническому виду, вводя
в каждое неравенство дополнительную переменную ![]() ,
,
![]() . Получим систему линейных
уравнений:
. Получим систему линейных
уравнений:
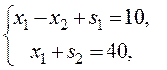 (5.16)
(5.16)
Целевая функция принимает вид
![]() (5.12)
(5.12)
Результаты последовательных итераций записываем в симплекс-таблицу.
Таблица 5.2
|
|
i |
|
|
|
2 |
1 |
0 |
0 |
|
|
|
1 |
2 |
3 |
4 |
|||||
|
|
|
|
|
|
|||||
|
0 |
1 2 |
3 4 |
0 0 |
10 40 |
1 1 |
-1 0 |
1 0 |
0 1 |
10 40 |
|
|
|
-2 |
-1 |
0 |
0 |
k=1 l=1 |
|||
|
|
1 2 |
1 4 |
2 0 |
10 30 |
1 0 |
-1 1 |
1 -1 |
0 1 |
- 30 |
|
|
|
0 |
-3 |
2 |
0 |
k=2 l=2 |
|||
|
|
1 2 |
1 2 |
2 1 |
40 30 |
1 0 |
0 1 |
0 -1 |
1 1 |
- - |
|
|
|
0 |
0 |
-1 |
3 |
k=3
|
|||
Из
симплекс-таблицы при S=2 следует, что согласно шагу 3 симплекс-алгоритма
данная ЗЛП не имеет конечного решения, т.к. отрицательная симплекс-разность ![]() соответствует столбцу
соответствует столбцу ![]() , все элементы которого
неположительны. Следовательно,
, все элементы которого
неположительны. Следовательно,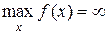 .
.
5.5. Задачи и упражнения
5.5.1.
Предприятие производит 3 вида продукции: А1, А2, А3,
используя сырье двух видов: В1 и В2. Известны затраты сырья
i-го вида на единицу изделия j-го вида (![]() ),
количество сырья каждого вида
),
количество сырья каждого вида ![]() (i=1,2),
а так же прибыль, полученная от единицы изделия j-го вида сj
(j=1,2,3).
(i=1,2),
а так же прибыль, полученная от единицы изделия j-го вида сj
(j=1,2,3).
Сколько изделий каждого вида необходимо произвести, чтобы получить: 1) максимум прибыли;
2) максимум товарной продукции?
Обозначения для вариантов: в таблице приведена матрица затрат: А=(аij), справа от таблицы значение bi (i=1,2) и внизу - сj (j=1,2,3).
у меня четвертый вариант
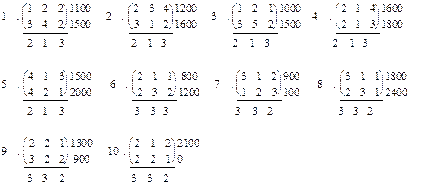
3) Решить задачу при дополнительных условиях: предприятие платит за хранение единицы сырья В1 и В2 соответственно 0,1 и 0,3 денежных единицы.
4) Решить задачу при условии, что задан план выпуска изделий. При решении учитывать возможность перевыполнения плана.
4. (200, 100, 250)
5.5.2. Решить симплекс-методом задачу из п 1.5.1.
5.5.3. Решить симплекс-методом задачу из п 1.5.2.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.