
 Лабораторная
работа №1
Лабораторная
работа №1
"Системы счисления, используемые в ЭВМ"
Цель:
1. Ознакомиться с видами систем счисления.
2. Научиться выполнять арифметические действия с числами в различных системах счисления.
3. Научиться выполнять перевод чисел из одной системы счисления в другую.
Основные понятия:
Системы счисления - это системы, созданные человеком. Такие системы называют искусственными, в отличие от ечественных систем, созданных природой.
К естественным (природным) системам относятся Галактики, Солнечная система.
К искусственным системам относятся города, заводы, система образования и т.п.
В свою очередь искусственные системы можно разделить на:
- материальные (автомобили, самолеты, дома, плотины и т.п.)
- общественные, т.е. различные объединения людей( парламент, группа, класс и т.п.)
- информационные ( национальные языки, Internet, системы счисления и т.п.).
Любая искусственная система создается с определенной целью. Целью создания системы счисления является выработка наиболее удобного способа записи чисел. Понятие числа - функциональное понятие как математики, так и информатики. Сегодня для записи чисел используется в основном десятичная система счисления.
Системой счисления называется совокупность приемов и правил представления числе с помощью цифровых знаков.
Все системы счисления делятся на два типа:
В позиционных системах счисления значения любой цифры зависит от ее положения ( позиции) в ряду цифр, изображающих это число.

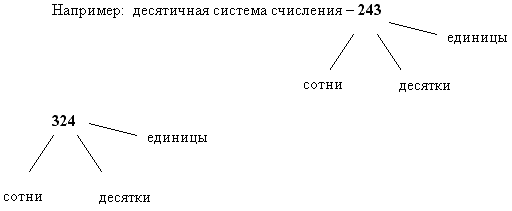
В непозиционных системах счисления значение любой цифры не зависит от занимаемой ее позиции

2) Единичная система (10-11 тыс.лет до н.э.)
1111111
3) Древнеегипетская десятичная непозиционная система
Число 321 записывалось![]()
![]()
В данном случае значение цифры не зависит от ее местоположения в числе, а действуют только арифметические действия "+" и "-".
Позиционные системы счисления включают определенное количество цифр, используемых для изображения числа, называемое - основанием системы счисления.
В зависимости от основания - системы счисления могут быть:
ДЕСЯТИЧНЫЕ - включают набор цифр 0,1,2,3,4,5,6,7,8,9 основание 10
ВОСЬМИРИЧНЫЕ - включают набор цифр 0,1,2,3,4,5,6,7 основание 8
ДВОИЧНЫЕ - включают набор цифр 0 и 1 основание 2
ШЕСТНАДЦАТИРИЧНЫЕ - включают набор цифр и букв 0-9 и A,B,C,D,E,F основание 16
 В общем случае любое число ,представленное в позиционной
системе счисления можно записать в виде полинома
В общем случае любое число ,представленное в позиционной
системе счисления можно записать в виде полинома
![]()
Данная запись используется для перевода любого числа из любой системы счисления в десятичную систему счисления.
Крайняя правая цифра называется его младшим разрядом, или наименьшим значащим разрядом; а крайняя левая старшим.
Рассмотрим формулу на примерах:
12310 = 1*102 + 2*101 + 3*100 = 100+20+3 = 12310
908,6110 = 9*102 + 0*101 + 8*100 + 6*10-1 + 1*10-2 = 900+8+0,6+0,01 = 908,6110
1101,112 = 1*23 + 1*22 + 0*21 + 1*20 + 1*2-1 + 1*2-2 = 8+4+1+0,5+0,25 = 13,7510
175,638 = 1*82 + 7*81 + 5*80 +6*8-1 + 3*8-2 = 64+56+5+6/8+3/16 = 125,937510
A1F,9616 = A*162 + 1*161 + F*160 + 9*16-1 + 6*16-2 = 2560+16+15+0,5625+0,0234=25911,585910
Арифметические действия в позиционных системах счисления
 сложение в двоичной системе счисления
сложение в двоичной системе счисления
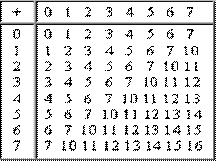 сложение в восьмеричной системе счисления
сложение в восьмеричной системе счисления

 сложение в шестнадцатеричной системе счисления
сложение в шестнадцатеричной системе счисления
Пример сложения в системах счисления:
![]()
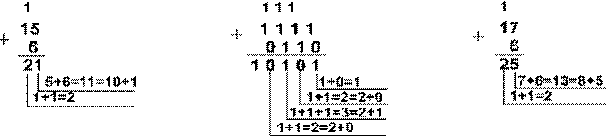
|
Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр). |
Например:

|
|
Например,
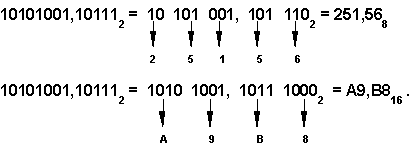
|
Перевод в десятичную
систему числа x,
записанного в q-ичной
cистеме счисления (q =
2, 8 или 16) в виде xq = (anan-1
... a0 , a-1 a-2
... a-m)q сводится к вычислению значения
многочлена x10 = an qn + an-1 qn-1 + ... + a0 q0 + a-1 q -1 + a-2 q-2 + ... + a-m q-m
|
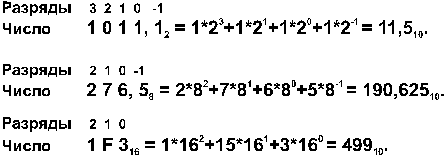
|
Для перевода целого десятичного числа N в систему счисления с основанием q необходимо N разделить с остатком ("нацело") на q , записанное в той же десятичной системе. Затем неполное частное, полученное от такого деления, нужно снова разделить с остатком на q , и т.д., пока последнее полученное неполное частное не станет равным нулю. Представлением числа N в новой системе счисления будет последовательность остатков деления, изображенных одной q-ичной цифрой и записанных в порядке, обратном порядку их получения. |
 Пример: Переведем число 75 из десятичной системы в двоичную,
восьмеричную и шестнадцатеричную:
Пример: Переведем число 75 из десятичной системы в двоичную,
восьмеричную и шестнадцатеричную:
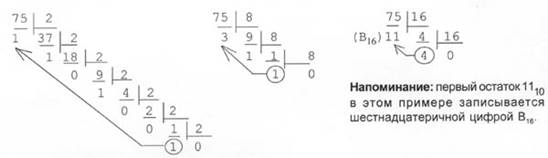
Ответ: 7510 = 1 001 0112 = 1138 = 4B16.
Задания
Вариант 1.
![]()
4. Оформить отчет по лабораторной работе.
Вариант 2.
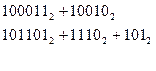
4. Оформить отчет по лабораторной работе.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.