
Системы счисления родственные двоичной.
Введение.
На ранних этапах развития вычислительной техники программы писали в машинных кодах, то есть без использования языков программирования. Для обозначение кодов операций машина оперирует с довольно длинными двоичными числами. Программисту трудно было работать с таким количеством знаков. Поэтому стали использовать системы счисления, которые с одной стороны относительно малозначны. А с другой обеспечивают легкий перевод чисел в двоичную систему и обратно. Такими системами являются системы, родственные двоичной.
Система называется родственной двоичной, если ее основание является степенью числа 2. К таким системам относятся четверичная, восьмеричная и шестнадцатеричная. Мы рассмотрим восьмеричную и шестнадцатиричную системы.
Восьмеричная система.
Основание р=8. База — цифры от 0 до 7.
Посчитаем в восьмеричной системе и сравним ее с десятичной.
|
10-я |
8-я |
10-я |
8-я |
10-я |
8-я |
10-я |
8-я |
|
0 |
0 |
5 |
5 |
10 |
12 |
15 |
17 |
|
1 |
1 |
6 |
6 |
11 |
13 |
16 |
20 |
|
2 |
2 |
7 |
7 |
12 |
14 |
17 |
21 |
|
3 |
3 |
8 |
10 |
13 |
15 |
18 |
22 |
|
4 |
4 |
9 |
11 |
14 |
16 |
19 |
23 |
Поскольку двоичная и восьмеричная системы являются родственными, каждая цифра восьмеричной системы может быть переведена в двоичную систему независимо от остальных цифр. Для этого нужно составить таблицу соответствия цифр восьмеричной системы двоичным числам, только двоичные числа должны быть представлены в виде триад, то есть совокупности из трех цифр.
|
2-а |
8-я |
2-я |
8-я |
|
000 |
0 |
100 |
4 |
|
001 |
1 |
101 |
5 |
|
010 |
2 |
110 |
6 |
|
011 |
3 |
111 |
7 |
Для восьмеричного числа перевода в двоичную систему нужно каждую цифру представить ее двоичным эквивалентом согласно таблице.
Пример: 567,238=101 110 111, 010 0112.
Для перевода двоичного числа в восьмеричную систему необходимо разделить число по триадам от запятой вправо и влево и каждую триаду представить восьмеричной цифрой согласно таблице. При необходимости слева до запятой и справа после запятой можно дописывать незначащие нули.
Пример: 1110100,1111012=001 110 100 111 1012=164,758.
Для перевода целого десятичного числа в восьмеричную необходимо выполнить последовательное деление на 8 до тех пор, пока результат не станет меньше 8. Последний результат и остатки, взятые в обратном порядке дадут восьмеричное число.
Пример: 98610=17328.
Для перевода правильной дроби из 10-системы счисления в 8-ю СС нужно умножить исходную дробь и дробные части получающихся произведений на основание 8. Целые части получающихся произведений дают последовательность цифр, которая является представлением дроби в 8-ой системе счисления.
Для перевода восьмеричного числа в десятичную систему необходимо разложить его по степеням основания системы 8 и выполнить сложение.
Пример: ![]()
Шестнадцатеричная система.
Основание р=16. База — цифры от 0 до 9 и буквы A,B,C,D,E,F.
Посчитаем в этой системе
|
10-я |
16-я |
10-я |
16-я |
10-я |
16-я |
10-я |
16-я |
|
0 |
0 |
9 |
9 |
18 |
12 |
27 |
1B |
|
1 |
1 |
10 |
A |
19 |
13 |
28 |
1C |
|
2 |
2 |
11 |
B |
20 |
14 |
29 |
1D |
|
3 |
3 |
12 |
C |
21 |
15 |
30 |
1E |
|
4 |
4 |
13 |
D |
22 |
16 |
31 |
1F |
|
5 |
5 |
14 |
E |
23 |
17 |
32 |
20 |
|
6 |
6 |
15 |
F |
24 |
18 |
33 |
21 |
|
7 |
7 |
16 |
10 |
25 |
19 |
34 |
22 |
|
8 |
8 |
17 |
11 |
26 |
1A |
35 |
23 |
Каждая цифра шестнадцатеричной системы может быть переведена в двоичную систему независимо от остальных цифр. Для этого нужно составить таблицу соответствия цифр шестнадцатеричной системы двоичным числам только двоичные числа должны быть представлены в виде тетрад, то есть совокупности из четырёх цифр.
|
2-а |
8-я |
2-я |
8-я |
|
0000 |
0 |
1000 |
8 |
|
0001 |
1 |
1001 |
9 |
|
0010 |
2 |
1010 |
A |
|
0011 |
3 |
1011 |
B |
|
0100 |
4 |
1100 |
C |
|
0101 |
5 |
1101 |
D |
|
0110 |
6 |
1110 |
E |
|
0111 |
7 |
1111 |
F |
Для перевода шестнадцатеричного числа в двоичную систему нужно каждую цифру представить ее двоичным эквивалентом согласно таблице.
Пример: 56,А816=101 0110, 1010 10002.
Для перевода двоичного числа в шестнадцатеричную систему необходимо разделить число по тетрадам от запятой вправо и влево и каждую тетраду представить шестнадцатеричной цифрой согласно таблице. При необходимости слева до запятой и справа после запятой можно дописывать незначащие нули.
Пример: 111 0100 1110 0111, 11012=74E7,D16.
Для перевода целого десятичного числа в шестнадцатеричную систему необходимо выполнить последовательное деление на 16 до тех пор, пока результат не станет меньше 16. Последний результат и остатки, взятые в обратном порядке дадут шестнадцатеричное число.
Пример: 98610=3DA16.
Для перевода правильной дроби из 10-системы счисления в 16-ю СС нужно умножить исходную дробь и дробные части получающихся произведений на основание 16. Целые части получающихся произведений дают последовательность цифр, которая является представлением дроби в 16-ой системе счисления.
Для перевода шестнадцатеричного числа в десятичную систему необходимо разложить его по степеням основания системы 16 и выполнить сложение.
Пример: 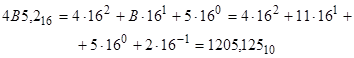
Арифметические действия с восьмеричными
и шестнадцатеричными числами.
Арифметические действия выполняются аналогично десятичной системе, но с учетом цифр, используемых в системе. Научиться проще всего на примере. Попробуем сложить:
7568+4528=14308
1А516+С3516=DDA16
7458+3638=13308
1F416+91116=B0516.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.