Системы уравнений как математические модели реальных ситуаций

Урок  по теме «Системы уравнений как математические модели реальных ситуаций».

алгебра 9 класс    УМК А.Г. Мордкович

учитель математики Брылова Н. В.

Цели:

1. Рассмотреть три этапа при решении задач, сводящихся к системам уравнений.
2. Формировать навыки в составлении математической модели на примере задач на движение.
3. Закрепить навык решения составленной модели
4. Рассмотреть задачи, решаемые с помощью систем уравнений для подготовки к ОГЭ математика.

План урока.

1.      Организационный момент.

2.      Проверка домашнего задания.

3.      Решение текстовых задач по теме урока.

4.      Дифференцированная парная работа по решению задач.

5.      Итог урока.

6.      Домашнее задание.

Ход урока.

1.      Организационный момент.

2.      Проверка домашнего задания. (У 2 учащихся решения проецируются на экран, совместное обсуждение предложенных решений)

3.      Решение текстовых задач на движение. (слайд 2)

·         Движение по реке.

№ 7. 3 ( учебник).  Моторная лодка против течения реки проплыла 10 км, а по течению 9 км, при этом по течению реки она шла 45 мин, а против течения – 1ч 15 мин. Найдите собственную скорость лодки и скорость течения реки.

1 этап

45 мин = ¾ ч

1ч 15 мин = 5/4 ч

S = V · t

2 этап

3 этап

10 км /ч собственная скорость лодки

2 км/ч скорость течения

Ответ 10 км/ч;  2 км/ч.

№7. 16 (учебник)

Турист проплыл на лодке по реке из города А в город В и обратно за 7 ч. Найдите скорость течения реки, если известно, что турист проплыл 2 км против течения за то же время, что и 5 км по течению, а расстояние между городами равно 20 км.

 1 этап

2 этап

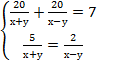
3 этап

7 км/ч собственная скорость лодки, 3 км/ч скорость течения

Ответ 3 км/ч

·         На движение.

№7.1 (учебник)

Из двух городов, расстояние между которыми 700 км, одновременно навстречу друг другу отправляются два поезда и встречаются через 5ч. Если второй поезд отправится на 7 ч раньше первого, то они встретятся через 2 ч после отправления первого поезда. Найдите скорость каждого поезда.

1 этап

2 этап

3 этап

80 км/ч скорость 1 поезда, 60 км/\ч скорость 2 поезда.

Ответ 80 км/ч, 60 км/ч

№1. Путь от посёлка до озера идёт сначала горизонтально, а затем в гору. От посёлка до озера велосипедист доехал за 1 ч, а обратно за 46 мин. Его скорость на горизонтальном участке была равна 12 км/ч, на подъёме – 8 км/ч, а на спуске – 15 км/ч. Найдите расстояние от посёлка до озера   (Задачи из ОГЭ   прошлых лет). (Слайд 3,4)

	П

2 этап

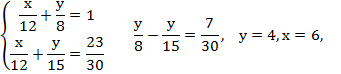
Ответ: 10 км.

4.      Дифференцированная парная работа по решению задач  ( задания на карточках, проверка в парах через экран) . (слайд 5,6,7)

Вариант А.

№1. Ре­ши­те си­сте­му урав­не­ний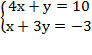   

В от­ве­те за­пи­ши­те сумму ре­ше­ний си­сте­мы.

№2. В классе 18 учащихся. Для поливки сада каждая девочка принесла по 2 ведра воды, а каждый мальчик – по 5 вёдер. Всего было принесено 57 вёдер воды. Сколько в классе девочек и сколько мальчиков?

Пусть в классе х девочек и у мальчиков. Какая система уравнений соответствует условию задачи?

Ответы: №1. 1;    №2. А

Вариант Б.

№1. Составьте математическую модель по заданному условию.

Мо­тор­ная лодка про­шла 36 км по те­че­нию реки и вер­ну­лась об­рат­но, по­тра­тив на весь путь 5 часов. Ско­рость те­че­ния реки равна 3 км/ч. Най­ди­те ско­рость лодки в не­по­движ­ной воде.

№2. Из города А в город В, расстояние между которыми 60 км, вышел пешеход. Через 3,5 часа навстречу ему выехал велосипедист, скорость которого на 14 км/ч больше скорости пешехода. Найдите скорости пешехода и велосипедиста, если они встретились ровно на середине пути между городами А и В.

Ответ: №1.    №2. 6 км/ч и 20 км/ч.

5.      Итог урока.

6.      Домашнее задание: УМК А. Г. Мордкович 9 класс П7 повторить, √ 22, 24, 6.20(а)  (слайд 8)