
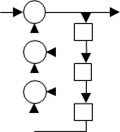
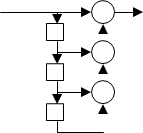
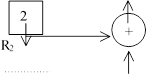
Рассмотрим цифровой скремблер и дескремблер. Это устройство для аппаратного шифрования и расшифровки последовательности бит из нулей и единиц. Простейшая реализация представляется в общем случае схемами из n-разрядного регистра сдвига и 1≤m≤n сумматоров по модулю 2, рис.1 и 2.

 Si Si +
Si Si +
выход L
![]()
![]() +
+
 R1
R1
+
![]()
![]() +
+
![]()
![]() +
+
![]()
![]() Rn
Rn
Рис. 1 Рис. 2
Так как логические переменные могут принимать только конечное число значений, в данном случае {0, 1}, и на множестве этих чисел определены операции сложения (XOR) и умножения (AND), то имеем частный случай поля Галуа. Это поле обладает замечательным свойством: операция вычитания в нём тождественна операции сложения.
Поля (последовательности) бит, например байт или слово, удобно рассматривать как многочлены. Например, байт представляется многочленом 7-й степени, каждый член которого соответствует ненулевому биту в байте:
(10010101) = 1*x7+0*x6 + 0*x5 + 1*x4 + 0*x3 + 1*x2 + 0*x1 + x0 = x7 + x4 + x2 + 1 .
Применение многочленов упрощает рассмотрение операций сдвига битовых полей. Битовое поле (последовательность) поступает на вход со старшего члена. Сдвиг данных в регистре в сторону выхода (как на рис. 1) соответствует умножению на x, а сдвиг данных в регистре в сторону входа (как на рис. 1) соответствует делению на x.
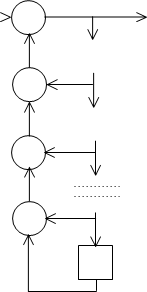
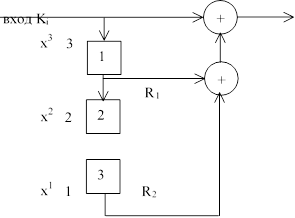
Свойства скремблера и дескремблера рассмотрим на примере схемы с трёхразрядным регистром и двумя сумматорами, рис. 3.
 Si
Si
S i = V + Ki
![]() V = R1 + R3 (1) R 1 = Ki-1
V = R1 + R3 (1) R 1 = Ki-1
R 3 = Ki-3
x0 0 R3
Пусть на вход поступает слово из пяти бит (K4K3K2K1K0) начиная со старшего бита, где Ki
= {0, 1}.
Составим таблицу потактовой работы схемы, согласно логическому алгоритму (1),
приведённому на рисунке.
|
Номер такта |
K |
R1 |
R2 |
R3 |
V |
S |
|
|
0 |
K4 |
0 |
0 |
0 |
0 |
K4 |
→x7 |
|
1 |
K4-1=K3 |
K4 |
0 |
0 |
K4 |
K4+K3 |
→x6 |
|
2 |
K4-2=K2 |
K3 |
K4 |
0 |
K3 |
K3+K2 |
→x5 |
|
3 |
K4-3=K1 |
K2 |
K3 |
K4 |
K2+K4 |
K4+K2+K1 |
→x4 |
|
4 |
K4-4=K0 |
K1 |
K2 |
K3 |
K1+K3 |
K3+K1+K0 |
→x3 |
|
5 |
K4-5=0 |
K0 |
K1 |
K2 |
K0+K2 |
K2+K0 |
→x2 |
|
6 |
K4-6=0 |
0 |
K0 |
K1 |
K1 |
K1 |
→x1 |
|
7 |
0 |
0 |
0 |
K0 |
K0 |
K0 |
→1 |
|
8 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
(…) |
(…) |
0 |
0 |
0 |
0 |
0 |
|
Итак, входное слово (читаем сверху вниз со старшего разряда): K(x) = K4K3K2K1K0 (2),
Выходное слово:
S(x) = K4<K4 + K3><K3 + K2><K4 + K2 + K1><K3 + K1 + K0><K2 + K0>K1K0 (3)
Тот же самый результат, но заметно проще и обобщённее получим на языке многочленов. На вход поступает слово (многочлен):
K(x) = K4*x4 + K3*x3 + K2*x2 + K1*x1 + K0 , где Ki = {0, 1}, ‘+’ – сумма по модулю 2.
Это слово умножается на многочлен, единичные биты которого определяются только теми сигналами с регистра, какие подаются на сумматоры. Так как на первое звено регистра подаётся старший бит входного слова, то нумеруем сигналы регистра (биты множителя) снизу вверх, как показано на рисунке 3.
На сумматоры подаются только биты номер 0, 2, 3. Следовательно, многочлен будет иметь вид:
g(x) = 1*x3 + 1*x2 + 0*x + 1 = x3 + x2 + 1.
Итак:
(K4*x4 + K3*x3 + K2*x2 + K1*x1 + K0)*(x3 + x2 + 1) = (K4*x7 + K3*x6 + K2*x5 + K1*x4 + K0* x3)
+ (K4*x6 + K3*x5 + K2*x4 + K1*x3 + K0* x2) + (K4*x4 + K3*x3 + K2*x2 + K1*x1 + K0) = K4*x7 + (K3 + K4)*x6 + (K2 + K3)*x5 + (K1 + K2 + K4)*x4 + (K0 + K1 + K3)*x3 + (K0 + K2)*x2 + K1*x + K0
= S(x) (5)
Выражение (5) совпадает с (3).
Итак, вообще: выходное слово есть произведение входного слова (многочлена (4)) и многочлена x3 + x2 + 1 = g(x).
S(x) = K(x)*g(x).
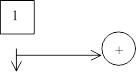
![]() Теперь
рассмотрим схему на рисунке 4.
Теперь
рассмотрим схему на рисунке 4.
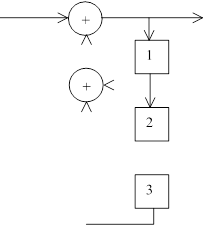 |
В этой схеме многочлен L(x) есть частное от деления многочлена входного слова S(x) на многочлен g(x) = x3 + x2 + 1:
![]() L(x) = S(x)
L(x) = S(x)
(8).
Это нетрудно увидеть, проведя анализ рисунка 4 подобно анализу рисунка 3. Интереснее убедиться в следующем. Подадим на вход схемы с рис.4 слово с выхода схемы с рис.3. тогда подставляя (6) в (8) получим:
L(x) = K(x).
Следовательно, если схему с рис.3 использовать как шифратор (скремблер), то схема с рис.4 исполняет роль дешифратора (дескремблера).
Действительно, поделим «углом» многочлен S(x) на многочлен g(x).
Обозначим:
a6 = K3 + K4, a5 = K2 + K3,
a4 = K1 + K2 + K4, a3 = K0 + K1 + K3, a2 = K0 + K2.
Тогда получим:
![]() K4*x7+a6*x6+a5*x5+a4*x4+a3*x3+a2*x2+K1*x+K0
│ x3+x2+0*x+1
K4*x7+a6*x6+a5*x5+a4*x4+a3*x3+a2*x2+K1*x+K0
│ x3+x2+0*x+1
+ │ K4*x4+K3*x3 +K2*x2+K1*x1+K0
![]() K4*x7+K4*x6+0*x5+K4*x4
K4*x7+K4*x6+0*x5+K4*x4
![]() │K3*x6+K3*x5+0*x4│+a3*x3
│K3*x6+K3*x5+0*x4│+a3*x3
+
![]() K3*x6+K3*x5+0*x4+K3*x3
K3*x6+K3*x5+0*x4+K3*x3
![]() │ K2*x5+(K1+ K2)*x4+(K0+
K1)*x3│+a2*x2
│ K2*x5+(K1+ K2)*x4+(K0+
K1)*x3│+a2*x2
+
![]() K2*x5+K2*x4+0*x3+K2*x2
K2*x5+K2*x4+0*x3+K2*x2
![]() │ K1*x4+(K0+ K1)*x3+
K0*x2│+K1*x
│ K1*x4+(K0+ K1)*x3+
K0*x2│+K1*x
+
![]() K 1*x4+K1*x3+0*x2+K1*x
K 1*x4+K1*x3+0*x2+K1*x
![]() │ K0*x3+K0*x2+0│+K0
│ K0*x3+K0*x2+0│+K0
+
![]() K0*x3+K0*x2+0+K0
K0*x3+K0*x2+0+K0
0+0+0
В схеме деления сразу учтено, что ,например, a6 + K4 = K3 + K4 + K4 = K3 и так далее, так как здесь работает арифметика поля Галуа, определённая для множества {0, 1}, в которой операция вычитания тождественна операции сложения. А операция сложения здесь (на языке работы цифровых схем) есть сложение по модулю 2.
На схеме деления многочленов «углом» рамочками выделены последовательные частичные остатки.
Видим, что в данном случае деление осуществилось без остатка, и частное от деления как раз и есть восстановление входного для схемы с рис.2 слова K(x).
В общем случае для схемы на рисунке 4 после окончания деления в ячейках регистра будут записаны коэффициенты остатка.
Как видно из формул (6) и (8), пара схем на рисунках 3 и 4 обладает с позиции шифрации/дешифрации последовательностей битовых слов свойством перестановки. То есть, если использовать схему с рис. 3 как скремблер, тогда схема с рис.4 будет
дескремблером. И, наоборот, если скремблировать информацию схемой с рис.4, то схему с рис.3 можно использовать как дескремблер.
Обратим внимание на ещё два замечательных свойства скремблера и дескремблера.
1) Если на вход скремблера постоянно подавать константу (0 или 1) , то на выходе под действием тактовых импульсов сдвига будет генерироваться псевдослучайная последовательность нулей и единиц, определяемая конфигурацией схемы и начальным состоянием регистра.
Для задач шифрования информации, чем длиннее эта собственная псевдослучайная последовательность (далее будем говорить «слово скремблера»), тем сложнее расшифровка.
2) Структура скремблер/дескремблер обладает свойством самосинхронизации. Если при включении структуры скремблер/дескремблер, то есть в начале работы, регистр скремблера и регистр дескремблера оказались в разных состояниях, то после приёма n последовательных бит (n равно ил меньше длины слова скремблера) регистр дескремблера окажется в том же состоянии, что имел регистр скремблера, и сигнал на выходе дескремблера начнёт точно повторять сигнал на входе скремблера.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.