Сложение векторов

Использование информационных технологий и исследовательская деятельность учащихся с применением программы «1С: Математический конструктор 3.0» при проведении урока математики (алгебра) в 8 классе.

Сценарий проведения урока:

Тема урока: “Сложение векторов. Правило параллелограмма. Сложение сил.”

Тип урока: Урок-презентация, изучение нового материала. При создании презентации использована программа «1С:Математический конструктор 3.0»

Цели:

объяснить учащимся правила сложения векторов;
научить применять полученные знания при решении геометрических и физических задач;
установление межпредметных связей;
воспитание у учащихся культуры мышления, информационной культуры;
воспитание критического отношения к знаниям, умения делать выводы, применять полученные знания.

ХОД УРОКА

I. Организационный момент.

II. Актуализация знаний.

Слайд 2.

III. Сообщение темы и цели урока.

IV. Теоретическое сообщение учителя (беседа с учащимися).

В работах математиков XIX в. У. Гамильтона, Г. Гроссмана и других были введены векторы, которые ранее в трудах Архимеда, Г. Галилея и других корифеев науки имели лишь механический смысл, а теперь приобрели права гражданства в математике.

Слайд 3,4.

С 60-х гг. нашего столетия векторы заняли прочное место и в школьном курсе геометрии. Применяемые в рамках евклидовой геометрии векторные методы значительно упрощают доказательства многих теорем и решение задач. Но роль векторов – не только в упрощении трудных мест школьного курса. Гораздо важнее то, что векторные методы находят сейчас широкие применения в физике, химии, экономике, биологии, не говоря уже о многих разделах современной математики (функциональный анализ и топология).

Векторы применяются в классической механике Галилея-Ньютона (в ее современном изложении), в теории относительности, квантовой физике, в математической экономике и многих других разделах естествознания, не говоря уже о применении векторов в различных областях математики.

В механике, в том числе и в кинематике, при описании движения тел широко используются векторные величины, поэтому необходимо уметь выполнять действия с ними.

Рассмотрим первое действие с векторами – сложение.

V. Объяснение новой темы.

Поскольку вектор характеризуется не только числовым значение, но и направлением, сложение векторов не подчиняется правилам сложения чисел. Например, пусть длины векторов a = 3 м, b = 4 м, тогда a + b = 3 м + 4 м = 7 м. Но длина вектора $\vec c = \vec a + \vec b$ не будет равна 7 м

Для того чтобы построить вектор $\vec c = \vec a + \vec b$ , применяются специальные правила сложения векторов.

Правило треугольника.

Слайд 5.

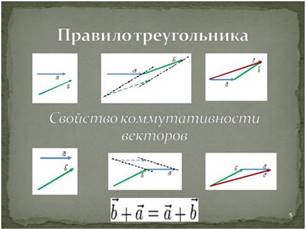
В зарубежной литературе этот метод называют «хвост к голове».

Для того чтобы сложить два вектора $\vec a$ и $\vec b$ нужно переместить вектор $\vec b$ параллельно самому себе так, чтобы его начало совпадало с концом вектора $\vec a$ . Тогда их суммой будет вектор $\vec c$ , начало которого совпадает с началом вектора $\vec a$ , а конец — с концом вектора $\vec b$ .

Результат не поменяется, если перемещать вместо вектора $\vec b$ вектор $\vec a$ , т.е. $\vec b + \vec a = \vec a + \vec b$ (свойство коммутативности векторов).

А длину вектора суммы $\vec c = \vec a + \vec b$ определяют по теореме косинусов $c = \sqrt{a^2+b^2-2a\cdot b\cdot \cos \alpha}$ , где $\alpha\,$ – угол между векторами $\vec a$ и $\vec b$ .

При помощи правила треугольника можно сложить два параллельных вектора $\vec a$ и $\vec b$ и $\vec a$ и $\vec d$ .

Слайд 6.

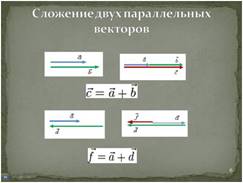
Суммы этих векторов $\vec c = \vec a + \vec b$ и $\vec f = \vec a + \vec d$ изображены на слайде. Причем, модули векторов c = a + b и $f=\left|a-d\right|$ .

Слайд 7.

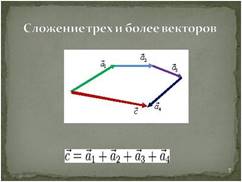
Правило треугольника можно применять при сложении трех и более векторов. Например, $\vec c = \vec a_1 + \vec a_2 +\vec a_3 +\vec a_4$ .

IV. Первичное закрепление.

Задача 1. Турист прошел 20 км на восток из города А в город В, а потом 30 км на восток в город С. Выбрав подходящий масштаб, начертите векторы и .
Равны ли векторы + и ?

Задача 2. Вертолет, пролетев в горизонтальном полете по прямой 40 км, повернул под углом 90° и пролетел еще 30 км. Найдите путь и перемещение вертолета.

VI. Сложение сил.

Слайд 8.

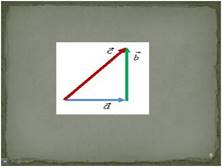
Силу, приложенную к телу, удобно изображать вектором, направление которого совпадает с направлением действия силы, а абсолютная величина пропорциональна величине силы. Как показывает опыт, при таком способе изображения сил равнодействующая двух или нескольких сил, приложенных к телу в одной точке, изображается суммой соответствующих им векторов. К телу в точке А приложены две силы, изображенные векторами $\vec a$ и $\vec b$ . Равнодействующая этих сил изображается вектором $\vec c = \vec a + \vec b$ .

Слайд 9.

Рассмотрим задачу, составленную по известной басне Ивана Кралова «Лебедь, рак и щука»

Слайд 10.

Представим силы, действующие на воз с поклажей в виде векторов:

Слайд 11.

Нужно определить, при каких усилиях действующих лиц воз все-таки сдвинется с места. Для дальнейшего построения и исследования задачи мы будем использовать программу «1С:Математический конструктор 3.0»

Используя меню Геометрия построим три луча, отметим на них отрезки одинаковой длины:

Слайд 12.

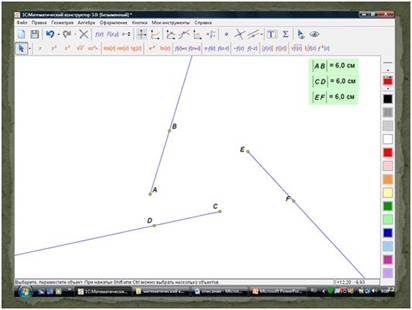
Луч АВ – усилие, прилагаемое Лебедем, луч СD – Раком, а луч ЕF – Щукой. По условию задачи сумма этих трех векторов равна 0 – воз не двигается! Найдем сумму векторов, выполняя параллельный перенос векторов ЕF и СD

Слайд 13, 14.

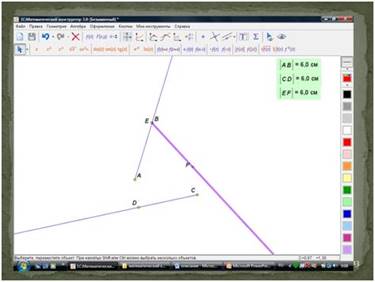
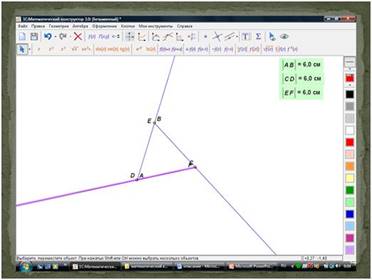
Давайте посмотрим, как изменится суммарная сила, действующая на воз, если увеличить усилия Щуки, а Лебедь и Рак будут действовать так же.

Для этого, объединим точки Е и В и точки С и F.

Увеличивая значение вектора ЕF, перемещая точку F мы обнаружим, что будет меняться и направление и величина вектора AD- воз сдвинется с места!

Слайд 15,16.

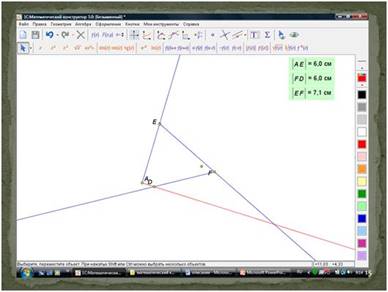
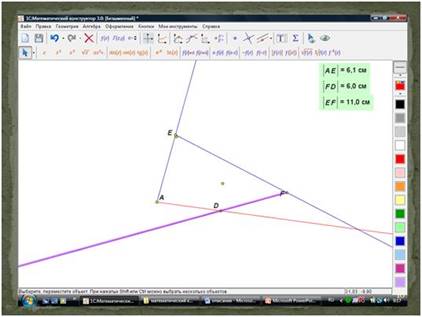
Задание: используя компьютер и программу «1С:Математический конструктор 3.0» исследуйте самостоятельно, как будет меняться суммарное усилие на воз при увеличении усилия Рака или Лебедя.

Учащиеся проводят самостоятельное исследование и представляют свои работы, используя компьютер и интерактивную доску:

IX. Домашнее задание: п.79, 80. № 762 (а).

X. Подведение итогов урока и выставление оценок.

Литература

1. Атанасян Л.С., Бутузов В.Ф. Геометрия, учебник для 7–9 классов средней школы. – М.: Просвещение, 2008.

2. Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика, 10 класс. – М.: Просвещение, 2008.

3. http://obr.1c.ru/mathkit/

4. Скачано с www.znanio.ru

Использование информационных технологий и исследовательская деятельность учащихся с применением программы «1С:

Слайд 2. III. Сообщение темы и цели урока

Рассмотрим первое действие с векторами – сложение

Суммы этих векторов и изображены на слайде

Рассмотрим задачу, составленную по известной басне

Слайд 12. Луч АВ – усилие, прилагаемое

Давайте посмотрим, как изменится суммарная сила, действующая на воз, если увеличить усилия

Задание: используя компьютер и программу «1С:Математический конструктор 3

X. Подведение итогов урока и выставление оценок

Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

26.05.2023