
Все зависимости, полученные выше для идеальных газов, справедливы и для их смесей, если в них подставлять газовую постоянную, молекулярную массу и теплоемкость смеси.
Закон Дальтона. В инженерной практике часто приходится иметь дело с газообразными веществами, близкими по свойствам к идеальным газам и представляющими собой механическую смесь отдельных компонентов различных газов, химически не реагирующих между собой. Это так называемые газовые смеси. В качестве примера можно назвать продукты сгорания топлива в двигателях внутреннего сгорания, топках печей и паровых котлов, влажный воздух в сушильных установках и т. п.
Основным законом, определяющим поведение газовой смеси, является закон Дальтона: полное давление смеси идеальных газов равно сумме парциальных давлений всех входящих в нее компонентов:
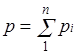
Парциальное давление pi — давление, которое имел бы газ, если бы он один при той же температуре занимал весь объем смеси.
Способы задания смеси. Состав газовой смеси может быть задан массовыми, объемными или мольными долями.
Массовой долей называется отношение массы отдельного компонента Мi, к массе смеси М:
![]() .
.
Очевидно, что 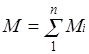
![]() и
и 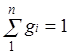 .
.
Массовые доли часто задаются в процентах. Например, для сухого воздуха ![]() ;
; ![]() .
.
Объемная доля представляет собой отношение приведенного объема газа V, к полному объему смеси V: ![]() .
.
Приведенным называется объем, который занимал бы компонент газа, если бы его давление и температура равнялись давлению и температуре смеси.
Для вычисления приведенного объема запишем два уравнения состояния i-го компонента:
![]() ; (1)
; (1)
![]() .
.
Первое уравнение относится к состоянию компонента газа в Смеси, когда он имеет парциальное давление pi и занимает полный объем смеси, а второе уравнение — к приведенному состоянию, когда давление и температура компонента равны, как и для смеси, р и Т. Из уравнений следует, что
![]() .
(2)
.
(2)
Просуммировав соотношение (2) для всех компонентов смеси,
получим с учетом закона Дальтона 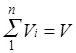 ,откуда
,откуда 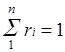 . Объемные доли также часто
задаются в процентах. Для воздуха
. Объемные доли также часто
задаются в процентах. Для воздуха ![]() ,
,![]() .
.
Иногда бывает удобнее задать состав смеси мольными долями. Мольной долей называется отношение количества молей Ni рассматриваемого компонента к общему количеству молей смеси N.
Пусть газовая смесь состоит из N1 молей первого
компонента, N2 молей второго компонента
и т. д. Число молей смеси 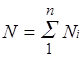 , а
мольная доля компонента
будет равна
, а
мольная доля компонента
будет равна ![]() .
.
В соответствии с законом Авогадро объемы моля любого газа при одинаковых
р и Т, в частности при температуре и давлении смеси, в идеально газовом состоянии одинаковы. Поэтому приведенный объем любого компонента может быть вычислен как произведение объема моля ![]() на число молей этого компонента, т. е.
на число молей этого компонента, т. е. ![]() а
объем смеси — по формуле
а
объем смеси — по формуле ![]() . Тогда
. Тогда ![]() , и, следовательно, задание смесильных
газов мольными долями равно заданию ее объемными долями.
, и, следовательно, задание смесильных
газов мольными долями равно заданию ее объемными долями.
Газовая постоянная смеси газов. Просуммировав уравнения
(1) для всех компонентов смеси, получим 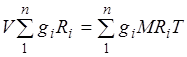 .
Учитывая
.
Учитывая 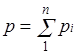 , можно записать
, можно записать
![]() ,
(3)
,
(3)
где
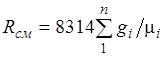 .
(4)
.
(4)
Из уравнения (3) следует, что смесь идеальных газов также
подчиняется уравнению Клапейрона. Поскольку ![]() то
из (4) следует, что газовая постоянная смеси [Дж/(кг-К)] имеет вид
то
из (4) следует, что газовая постоянная смеси [Дж/(кг-К)] имеет вид
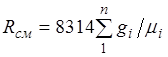 (5)
(5)
Кажущаяся молекулярная масса смеси. Выразим формально газовую постоянную смеси R, введя кажущуюся окулярную массу смеси ![]() :
: ![]() (6)
(6)
Сравнивая правые части соотношений (5) и (6), найдем
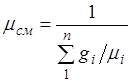 .
.
Из определения массовых долей следует, что
![]()
Просуммировав это соотношение для
всех компонентов и
учитывая, что 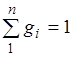 , получим выражение для кажущейся молекулярной и массы смеси, заданной объемными долями:
, получим выражение для кажущейся молекулярной и массы смеси, заданной объемными долями:
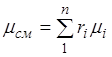 . (7)
. (7)
Соотношение между объемными и массовыми долями. Учитывая (7), получаем 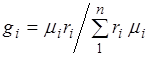 .
.
Поскольку 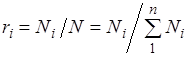 , то
, то
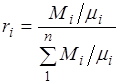
Разделив числитель и знаменатель этой формулы на массу смеси М, получим
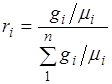 .
.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.