СПОСОБ ПОДСТАНОВКИ

способ подстановки

Цели: разобрать, в чём состоит способ подстановки решения систем линейных уравнений; вывести алгоритм применения этого способа; формировать умение решать системы уравнений способом подстановки.

Ход урока

I. Устная работа.

1. Является ли пара чисел (2; 3) решением системы уравнений:

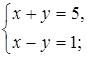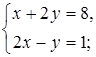а)                       б)                        в)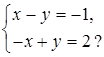

2. Сколько решений имеет система уравнений:

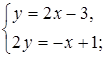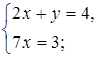а)                  б)                        в)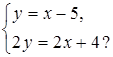

II. Объяснение нового материала.

Объяснение проводить согласно пункту 43 учебника.

1. Разобрать пример 1

2. Дать определение равносильных систем уравнений и привести их геометрическую интерпретацию.

3. записать в тетрадях алгоритм решения систем уравнений способом подстановки. При этом каждый шаг алгоритма должен отражаться соответствующим действием в решении системы уравнений.

III. Формирование умений и навыков.

1. Выразите в уравнениях х через у и у через х.

а) х + у = 5;                    в) х – 3у = –6;                     д) 5х – 2у = 0;

б) у – х = –2;                 г) –2х + у = 3;                      е) 3х + 5у = –7.

2. № 1068.

3. № 1069.

Для решения каждой системы следует вызывать к доске по одному учащемуся. Требовать, чтобы они вслух комментировали все шаги решения.

а)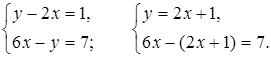

    6х – (2х + 1) = 7;

    6х – 2х – 1 = 7;

    4х = 8;

    х = 2;

    у = 2х + 1;

    у = 2 · 2 + 1 = 5.

Ответ: (2; 5).

в)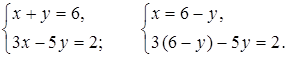

    3 (6 – у) – 5у = 2;

    18 – 3у – 5у = 2;

    –8у = –16;

    у = 2;

    х = 6 – у;

    х = 6 – 2 = 4.

Ответ: (4; 2).

IV. Итоги урока.

– Что называется решением системы уравнений с двумя переменными?

– Какие вы знаете способы решения систем уравнений?

– Сформулируйте алгоритм решения систем уравнений способом подстановки.

– Из какого уравнения системы лучше выражать переменную?

Домашнее задание: № 1070.