Некрасов В. Б., Санкт-Петербург www.решуегэ.рф

 

СПРАВОЧНЫЙ МАТЕРИАЛ

ПО  АЛГЕБРЕ И НАЧАЛАМ АНАЛИЗА

 

 

1. Формулы сокращенного умножения

 

(a b± )² = a² ± 2ab b+ ²                    (a b± )³ = a³ ± 3a b² + 3ab² ± b³ a² −b² = (a −b a)( + b)                            a³ ± b³ = (a ± b a)( ² ∓ ab + b² )

 

 

2. Модуль числа

 

⎧ a, если a ≥ 0,

                                                                 Определение: a = ⎨                         

_⎩−a, если a < 0.

 

Основные свойства модуля:

 

                                                                                                            ⎧| a a|≥ ,                      | a | = a ⇔ a ≥ 0,

           1. | a |≥ 0.                  2. | a | = −|  a |.                3. ⎨                                4.                             

                                                                                                            _⎩| a |≥−a.                    | a | = −a ⇔ a ≤ 0.

 

 

3. Степень с действительным показателем

 

a	x	ax
a∈	x∈ , x≥ 2	ax = a a⋅  ⋅...⋅a x сомножителей
a∈	x =1	a1 = a
a∈    ,  a ≠ 0	x=0	a0 =1
a∈    ,  a ≠ 0	x∈   , x < 0	1 ax = −x a
a ≥ 0	m x=  ,  m n, ∈ , n≥ 2 n	m a n = n am
a>0	m x=  ,  m n, ∈ , m< 0, n≥ 2 n	1 ax = −x a
a> 0	. x∈ .	ax = limaxn  ∗) n→∞

 

 

Свойства степени с действительным показателем

 

                         Пусть  a > 0, b > 0, x∈     , y∈     .  Тогда верны следующие соотношения:

ax ⋅ay = ax y+	(ab)x = a bx ⋅ x	ax = ay ⇔ x = y a≠1
ax :ay = ax y−	( : )a b x = a bx : x	ax > ay ⇔ x > y a>1
y (ax ) = axy	ax > 0	ax > ay         ⇔    x < y 0< <a 1

                                                            

∗) {^x_n} ―  последовательность десятичных приближений числа  x ,  взятых с избытком или недостатком (здесь n ― число знаков после запятой в десятичной записи числа  x).

4. Корень n-ой степени из числа

 

Корнем  n-ой степени (n∈ , n ≥ 2) из числа  a  называется число,  n-ая степень которого равна  a.

Арифметическим корнем четной степени  n (n = 2k, k ∈          ) из неотрицательного числа a называется неотрицательное число, n-ая степень которого равна  a.

 

Основные свойства арифметического корня:

 

 

 

5. Логарифмы

 

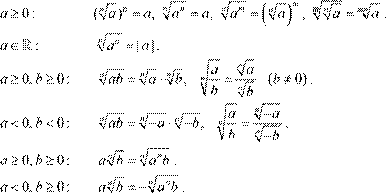
         Определение логарифма:              log_a b = c    ⇔   a^c = b .

a>0, a≠1 Основное логарифмическое тождество:    a^{loga b} = b.

 

 

Основные свойства логарифмов

 

Пусть  a > 0, a ≠1, b > 0, b ≠1, x > 0, y > 0, p∈       .  Тогда верны следующие соотношения:

 

log (_a xy) = ^log_a x+ ^log_a y               log_a x ^p = plog_a x                           log_a x = _log^logb^b _a^x log ( )_a     ^x_y = log_a x −log_a y               logap x = ¹_p log_a x ,   p ≠ 0              x^{loga y} = y^{loga x}

 

 

6. Арифметическая прогрессия

 

Формула  n-го члена арифметической прогрессии:       a_n = a₁ + d n( −1) .

an−1 + an+1 Характеристическое свойство арифметической прогрессии:    a = , n ≥ 2.

          Сумма  n  первых членов арифметической прогрессии     S_n =           n .

2

 

При решении задач, связанных с арифметической прогрессией, могут оказаться полезными также следующие формулы:

 

                        2a¹ + d n( −1)                           2an − d n( −1)                          an k− + an k+

               S_n = n;                S_n = n;                                        , k < n;

                                     2                                             2

a − a

ak + =an ak m− +an m+ , m k< ;                          d =         . n − k

 

7. Геометрическая прогрессия

 

         Формула  n-го  члена  геометрической прогрессии:      a_n = a q₁ ⁿ⁻¹ .

          Характеристическое свойство геометрической прогрессии:  .

a₁ − a q_n

          Сумма  n  первых членов геометрической прогрессии:     S_n =  ,  q ≠1.

1− q

При решении задач, связанных с геометрической прогрессией, могут оказаться полезными также следующие формулы:

 

                    a₁(1− qⁿ )                2

          S_n = ;           an = an k− an k+ , k < n ; a ak n = ak m n m− a + , m < k ;         | q | = n k−       .

1− q

 

 

8. Бесконечно убывающая геометрическая прогрессия

 

a¹

          Сумма бесконечно убывающей геометрической прогрессии: S = .

1− q

 

 

9.  Основные формулы тригонометрии

 

Зависимость между тригонометрическими функциями одного аргумента

 

                                              sin² α + cos² α =1                            tgαctgα =1

tgα =          1+ tg² α =        ¹                      ctgα =       1+ ctg² α = ₂                     

sin α

 

Формулы сложения

 

cos(α −β =)      cosαcosβ + sinαsinβ   tg(α +β =)       cos(α +β =)      cosαcosβ −sinαsinβ         tg(α −β =)       sin(α +β =)       sinαcosβ + cosαsinβ    ctg(α +β =)        

                              sin(α −β =) sinαcosβ − cosαsinβ                          ctg(α −β =)

 

 

Формулы тригонометрических функций двойного аргумента

 

                                           sin2α = 2sinαcosα                              cos2α = −1 2sin² α

                                       sin2α = 2tg2α                                    cos2α= 1−tg22 α

1+tg α           1+tg α cos2α = cos² α −sin² α tg2α = ^2tg₂^α

1−tg α

                                          cos2α = 2cos2 α −1                           ctg2α = ctg2ctg2 αα−1

 

Формулы понижения степени

 

sin² α =    tg² α =  cos² α =     ctg² α =  Формулы приведения

 

   Все формулы приведения получаются из соответствующих формул сложения. 

   П р и м е р  1.  cos(^π₂ + α =) cos cos^π₂ α −sin sin^π₂ α = −sinα .

Нет необходимости запоминать такое количество формул, так как их применение легко укладывается в следующую схему:

•        определяется координатная четверть, в которой лежит аргумент приводимой функции, считая, что  ;

•        определяется знак приводимой функции;

•        определяется название приведенной функции по следующему правилу: если аргумент приводимой функции имеет вид  (±α)  или  (±α) , то функция меняется на кофункцию, если аргумент приводимой функции имеет вид  (π± α) , то функция названия не меняет.

 

  П р и м е р  2.     

•          (IV четверть);

•           ⇒     + α <       ;

•        аргумент приводимой функции имеет вид  ( + α) , следовательно, название функции меняется.   Таким образом:  tg(+α =− α) ctg .

             

 

Формулы преобразования суммы тригонометрических функций в произведение

 

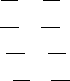sinα + sinβ = 2sin ^α+β₂ cos ^α−β₂ tgα + tgβ =  sinα −sinβ = 2sin ^α−β₂ cos ^α+β₂ tgα− β=tg  cosα + cosβ = 2cos ^α+β₂ cos ^α−β₂ ctgα + ctgβ =  

                               cosα − cosβ = −2sin ^α+β₂ sin ^α−β₂                                               ctgα −ctgβ =  

 

 

Формулы преобразования произведения тригонометрических функций в сумму

 

cosαcosβ = (cos(α −β +) cos(α +β)) sinαsinβ = (cos(α −β −) cos(α +β)) sinα β=cos (sin(α+β +) sin(α−β))

 

 

10. Производная и интеграл

 

Таблица производных некоторых элементарных функций

 

Функция	Производная		Функция	Производная
c	0		loga x	1 , x > 0 xlna
kx + b	k
x p , p≠ 0, p≠1	px p−1		sin x	cosx
ex	ex		cosx	−sin x
ax	ax lna		tg x	1       cos2 x
ln x	1 , x> 0 x		ctg x	x

 

Правила дифференцирования:

 

( f ( )x + g x( ))^′ = f ′( )x + g x′( )

(cf x( ))^′ = cf ′( )x

( f ( ) ( )x g x )^′ = f ′( ) ( )x g x + f x g x( ) ′( )

f    ( )x ′    f ′( ) ( )x g x − f x g x( ) ′( )

                                                                              (   ) =                     

g   x( )           g2( )x

                                                                      [ f ( ( ))g x ]^′ = f ′( ( ))g x g x′( )

 

 

Уравнение касательной к графику функции y = f x( ) в его точке (x₀; f x( ₀ )):

 

y = f ′(x₀ )(x − x₀ ) + f x( ₀ )

 

 

Таблица первообразных для некоторых элементарных функций

 

Функция	Первообразные		Функция	Первообразные
a	ax + C		ax	x C
x p , p ≠ −1	xp     C p		sin x	−cosx + C
1 , x> 0 x	ln x + C		cosx	sin x + C
1 , x < 0 x	ln(−x) +C		1       cos2 x	tg x +C
ex	ex +C		1      sin2 x	−ctg x + C

 

 

 

Правила нахождения первообразных

 

Пусть F( )x , G x( ) ― первообразные для функций f ( )x и g( )x соответственно, a, b, k ― постоянные,  k ≠ 0 .  Тогда:   

 

F( )x + G x( ) ― первообразная для функции  f ( )x + g x( );

 

aF x( ) ― первообразная для функции  af x( );

 

¹k F(kx + b) ― первообразная для функции  f (kx + b) .

 

b

Формула Ньютона-Лейбница: ∫ f ( )x dx = F b( ) − F a( ) .

a