
Дифференциальные уравнения
Дифференциальным уравнением называется уравнение , в котором содержится независимая переменная х ,искомая функция у и ее производные ( или дифференциалы функции и аргумента).
![]() дифференциальное уравнение
порядка.
дифференциальное уравнение
порядка.
Порядком дифференциального уравнения является наивысший порядок производных, входящих в данное уравнение. Общим решением дифференциального уравнения называется функция
y=![]() ) , обращающая данное уравнение
в тождество. Количество постоянных зависит от порядка уравнения.
) , обращающая данное уравнение
в тождество. Количество постоянных зависит от порядка уравнения.
Частным решением дифференциального уравнения ![]() называется решение, полученное
из общего решения при фиксированных значениях постоянных
называется решение, полученное
из общего решения при фиксированных значениях постоянных ![]()
Дифференциальные уравнения с разделяющими переменными
Пусть ![]() -дифференциальное уравнение с
разделяющимися переменными. Заменим у′=
-дифференциальное уравнение с
разделяющимися переменными. Заменим у′=![]() , тогда уравнение примет вид:
, тогда уравнение примет вид:![]() ,
,
разделим переменные ![]() проинтегрируем
обе части уравнения
проинтегрируем
обе части уравнения ![]()
Получим общее решение: ![]()
Пример 1. Решение уравнение ![]() и найти его частное решение,
удовлетворяющее условие y=3, при
и найти его частное решение,
удовлетворяющее условие y=3, при ![]()
Решение: т.к.![]() Разделим переменные
Разделим переменные ![]()
Интегрируя обе части уравнения, получим ![]()
Пропотенцировав, получим ![]() - общее решение. Найдем частное
решение при
- общее решение. Найдем частное
решение при ![]()
Частное решение имеет вид ![]()
Ответ: ![]()
Пример 2. Решение дифференциальное уравнение 2-го порядка
![]()
его частное решение при ![]()
Решение: Уравнения такого типа решается методом двойного интегрирования.
Обозначим ![]()
Проинтегрируем данное уравнение![]() Получим
Получим ![]() Заменим
Заменим 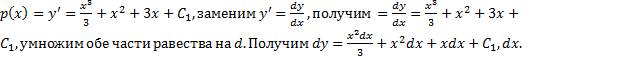
Проинтегрируем уравнение
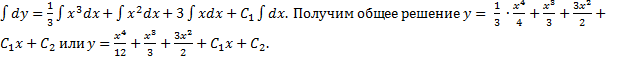
Подставим в уравнение ![]()
Подставим в общее решение значения ![]() и найдем значение
и найдем значение ![]()
![]()
Подставим значения ![]() в общее решение и получим
частное решения
в общее решение и получим
частное решения ![]()
Ответ: ![]() – общее решение,
– общее решение,
![]()
схема решения дифференциального уравнения первого порядка с разделенными переменными
 |
|
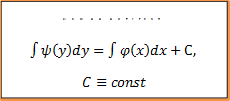 |
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.