Статья: Раскраска карт на поверхностях

С.В. Сазонова

г. Москва

ГАОУ ВО МГПУ

Руководитель: В.Г. Покровский, доцент, кандидат физико-математических наук

РАСКРАСКА КАРТ НА ПОВЕРХНОСТЯХ

Допускает ли любая карта, изображенная на сфере, раскраску в 4 цвета так, чтобы соседние страны[1] были различного цвета? В научном мире первый вопрос, связанный с раскраской, появился в 1852 году, когда Аугуст де Морган написал письмо коллеге о том, что один из его студентов задал ему такую задачу, и де Морган не смог ее решить. Студент Лондонского университета Френсис Гутри удостоверился, что карту графств Англии можно раскрасить в 4 цвета, и задумался о такой возможности для произвольных абстрактных карт.

 После почти тридцатилетнего перерыва в 1879 и 1880 годах Тейтом и Кемпе были опубликованы доказательства гипотезы о четырех красках. Это доказательство считалось верным целых 10 лет, пока английский математик Перси Джон Хивуд, не только нашел пробелы в доказательствах коллег, но и привел доказательство для раскраски карт в 5 цветов (о том, что любую карту на сфере можно раскрасить в пять цветов, чтобы соседние не были одного цвета). Для четырех красок это утверждение было установлено с помощью компьютера лишь в 1976 году [1, с. 75-76].

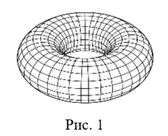
Но все эти попытки доказательств были для карт, расположенных на плоскости или сфере. Хивуд первым стал рассматривать карты на торе – ином теле, подобном пончику или велосипедной камере (рис.1).      

Теперь представим сферу с приделанными к ней ручками (рис. 2). Такая сфера с p ручками называется ориентируемой поверхностью рода p и обозначается через  (пример:  – это сфера,  – это тор). Наглядное описание ориентируемой поверхности сотоит в том, что такая поверхность имеет две стороны в отличие от неориентируемых односторонних поверхностей таких, как лист Мебиуса. Далее мы будем рассматривать только ориентируемые замкнутые поверхности.                                                                              

Теперь перейдем от карт на поверхностях к графам: представим, что страна – это вершина графа, а границы между странами – это ребра графа.

Определение 1. Граф состоит из конечного множества вершин и множества ребер, удовлетворяющих двум условиям: каждое ребро соединяет две различные вершины, и никакие два различных ребра не соединяют одну и ту же пару вершин.

Выясним, что значит изобразить граф на поверхности (вложить граф в поверхность). Рассмотрим конечное число многоугольников таких, что общее число сторон всех многоугольников четно. Пометим каждую из сторон буквами так, чтобы каждая из букв появлялась ровно на двух сторонах. Далее ориентируем с помощью направления стрелки каждую из сторон многоугольников, и отождествляем пары сторон так, чтобы направления стрелок совпали.

Определение 2. Полиэдр – это фигура, полученная из данных многоугольников склеиванием помеченных одной и той же буквой сторон в направлении стрелок.

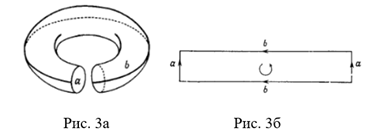
С помощью непрерывной деформации полиэдры можно преобразовывать в замкнутые поверхности. Рассмотрим такое преобразование на примере тора: разрежем тор вдоль одной из образующих его окружностей a и получим «согнутый» цилиндр, выпрямим его и разрежем вдоль образующей b (рис.3). Если мы поставим условие, что пара параллельных сторон отождествляется, и развернем по разрезам полученную поверхность, то получим прямоугольник со сторонами a и b (как показано на рисунках 3а и 3б).

Определение 3. Хроматическим числом графа G называется минимальное число цветов, в которые можно раскрасить вершины графа G так, чтобы концы любого ребра имели разные цвета. Хроматическое число обозначается через χ(G).

Определение 4. 1-скелетом полиэдра P называют граф, состоящий из всех ребер и всех вершин полиэдра P.

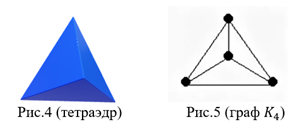
Пример: 1-скелет тетраэдра — это граф  (рис.4 и 5).

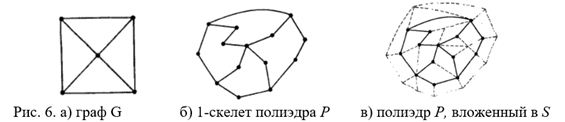
Определение 5. Будем говорить, что граф G можно вложить в поверхность S, если существует такой полиэдр P на поверхности S, что 1-скелет полиэдра P содержит подграф, гомеоморфный графу G (рис.6а, б, в). Другими словами, это означает, что граф G можно вложить в поверхность S, если можно его нарисовать на поверхности S без пересечения ребер.

Понятие гомеоморфных графов можно разобрать на примере рис.6а и 6б. Если граф G можно преобразовать в G’, убирая или добавляя вершины на ребрах графа G, то такие графы называются гомеоморфными.

Определение 6. Род 𝜸(G) графа G определяется как минимальный род ориентируемой поверхности, в которую его можно вложить, то есть 𝜸(G)=p, если граф G можно вложить в поверхность S_p. Пример: возьмем тетраэдр (рис.4), с помощью непрерывной деформации его можно преобразовать в сферу (S₀). 1-скелет тетраэдра — это граф  (рис.5), получается 𝜸(K₄)=0.

Возникает непростой вопрос: как найти род того или иного графа? В частичном решении этого вопроса нам поможет следующая числовая характеристика полиэдра.

Определение 7. Эйлеровой характеристикой полиэдра P называется знакочередующаяся сумма E(P) = -+, где ,  это соответственно числа вершин, ребер и многоугольников.

Теорема 1. Пусть в графе G каждая вершина принадлежит не менее, чем двум ребрам. Если граф G можно вложить в замкнутую поверхность S, то ≤3-3E(S), где a₀ – число вершин, а a₁ – число ребер графа G.

Теорема 2. Если G – критический граф с вершинами и  ребрами и хроматическое число графа G равно 𝜒, то выполняется соотношение (𝜒-1)≤2.

Определение 8. Граф G называется критическим, если хроматическое число любого его собственного подграфа меньше, чем хроматическое число графа G.

Теорема 3 (Неравенство Хивуда). Если S – замкнутая поверхность, отличная от сферы, то 𝜒(S) ≤ .

Доказательство. Согласно определению (5) найдется такой граф, который можно вложить в поверхность S и для которого будет выполняться 𝜒(S)=𝜒(G). Если считать, что G - критический граф, то из теоремы (2) следует, что для 𝜒(S) = 𝜒(G) и E(S)=E можно сделать следующие выводы: возьмем  из выражения ≤3-3E и подставим его в выражение (𝜒-1)≤2. Тогда получим (𝜒-1)≤6-6E, и, разделив это выражение на , получим 𝜒-1≤6- .

Далее будем рассматривать два случая: E≤0 и E=1. Если E ≤ 0: всвязи с тем, что ≥𝜒, можем заменить  на 𝜒: 𝜒-1≤6 - , умножим выражение на 𝜒 и после приведения подобных членов получим квадратное уравнение: - 7𝜒 + 6E ≤ 0. Разложив квадратный трехчлен на множители, получим неравенство: (𝜒 - )(𝜒 - ) ≤ 0. Оценим выражения в скобках: если E≤ 0, то  ≥ 7; далее, 𝜒 ≥ 1, значит второй множитель (𝜒 -  всегда положителен. И из того, что произведение этих двух скобок неположительное, следует 𝜒 -  ≤0. Это доказывает неравенство Хивуда для случая E≤0.

Рассмотрим второй  случай E=1. Это значит, что S – неориентируемая поверхность рода 1. Тогда верно утверждение 𝜒–1≤6-<6. И если мы вспомним, что 𝜒 – целое число, то найдем 𝜒≤6 =  = , что и требовалось доказать!

При формулировке этой теоремы Хивуд допустил некоторые ошибки, которые привели его к неверному выводу – он полагал, что доказал равенство. Работа Рингеля и Янгса превратила неравенство Хивуда в равенство: 𝜒(S) = , и последнее равенство имеет два названия: гипотеза Хивуда и теорема Рингеля [2]. В доказательстве рассмотрены 12 случаев: отдельно для каждого рода поверхности[2] по модулю 12.

Рассмотренная тема отлично подойдет для дополнительных занятий в школе: несмотря на то, что это элементы топологии, все можно преподнести достаточно просто, объясняя «на пальцах». Возможность иллюстрирования каждого определения делает материал более наглядным и понятным, а интересная и незамысловатая постановка проблемы заинтересует школьников разных возрастов. Эта статья может послужить основой для развития интереса школьников к дискретной математике и теории графов, которые можно смело начинать изучать на элективных занятиях.

Библиографический список

1.     Болтянский В. Г. Наглядная топология. Библиотечка «Квант», вып. 21. / В. Г. Болтянский, В. А. Ефремович – М.: Наука. 1982. – 160 с.

2.     Рингель Г. Теорема о раскраске карт: монография – М.: Мир, 1977. – 256 с.

Скачано с www.znanio.ru