Сумма первых п членов геометрической прогрессии

 

 

ГОАОУ « Траектория» г. Грязи, Липецкая область

 

 

 

 

 

 

 

 

 

 

 

 

 

Провела учитель математики : Т.А.Минакова

 

 

 

 

 

 

 

 

 

 

 

Тема: Сумма первых п членов геометрической прогрессии. Решение упражнений

Цель: совершенствование практических навыков применения формулы суммы первых п членов геометрической прогрессии при решении задач

Задачи:

образовательные - расширить и углубить знания о прогрессиях, продолжить формирование у учащихся умения применять формулу суммы n- первых членов геометрической  прогрессии при решении задач

развивающие - способствовать развитию наблюдательности, умения анализировать, применять  приемы сравнения, переноса знаний  в новую ситуацию; развитию логического мышления, творческих способностей учащихся путем решения межпредметных  задач, формировать умения чётко и ясно излагать свои мысли

воспитательные - побуждать учащихся к преодолению трудностей, самоконтролю, взаимоконтролю; воспитывать познавательную активность, стремления расширять свой кругозор; формировать умения аккуратно и грамотно выполнять математические записи.

Тип: урок применения знаний, умений и навыков

Оборудование: компьютер  и мульти медийное оборудование

Методическое  сопровождение:  компьютерная презентация

 

Ход урока

I.    Организационный момент.

 

II. Актуализация опорных знаний

1.      Фронтальная беседа

На прошлом уроке мы познакомились с формулой – …

Давайте вспомним, какая прогрессия называется геометрической …

 

2.      Проверка теоретических знаний учащихся

 

Я предлагаю вам составить шпаргалку к ГИА

 

Один из учеников читает свойство, второй называет номер формулы, а третий, используя магниты, заполняет таблицу

 

 

 

 

 

 

 

 

 

Прогрессия		Геометрическая
Рекуррентная формула	1
Свойство последовательных членов	2
Характеристическое свойство	3
Формула n-го члена	45
Формулы суммы n первых членов прогрессии	6     7

 

1) 

2) 

3)

4)

5)

6)

 

7)

 

3. Устно:

Выразите геометрической прогрессии через первый член.

Выразитегеометрической прогрессии через третий член.

 

Теперь мы с вами можем ответить на вопросы:

- Знаем ли мы теорию?

- Готовы ли мы к решению практических задач?

 

III. Мотивация учения школьников.

- Один мудрец сказал однажды: «Не для школы, а для жизни учимся».

           Я хочу, чтобы наш урок расширил ваши знания, принес много полезной информации, был для каждого из вас интересен.

Вместе с вами мы поднимемся еще на одну ступеньку по пути изучения темы «Геометрическая прогрессия», так как впереди нас ждет контрольная работа, а слово «Прогрессио» в переводе с греческого языка означает движение вперёд.

 

На сегодняшнем уроке мы продолжаем работать с формулой нахождения первых п членов геометрической прогрессии и совершенствованием свои  практические навыки применения формулы при решении задач.

 

Итак, приготовим тетради к работе. Записали в рабочих тетрадях:

Число.

Классная работа.

Тема урока

 

Ожидаемые результаты:

- Научиться применять формулы геометрической прогрессии на практике.

- Изучить в каких областях жизни используется геометрическая прогрессия.

- Решить задачи из разных областей знаний.

 

IV. Формирование умений и навыков.

На прошлом уроке вы получили задания для групп:

І группа - «Аналитики» – Задание: проанализировать задания сборника к ГИА.

Разбор практико-ориентированных задач.

ІІ группа - «Эксперты– Задание: использование геометрической прогрессии в разных науках.

ІІІ группа - «Практики» – Задание: геометрическая прогрессия в жизни

 

При подготовке к ГИА по математике мы используем сборник заданий для государственной итоговой аттестации по математике в 9 классе под редакцией М. И. Бурды, 2014 год.

 

І группа - «Аналитики».  Состав     человек.

Задание: проанализировать задания сборника к ГИА.

Представитель группы расскажет о результатах исследования.

 

Изучив и проанализировав сборник заданий, мы подсчитали, задачи на геометрическую прогрессию разной сложности встречаются в 36 вариантах. В первой тестовой части – в 8 вариантах, во второй части – в 20 вариантах, а третьей части – в 7 вариантах. Из них на сумму первых п членов геометрической прогрессии  - 24 варианта. Я предлагаю вам с членами нашей группы решить некоторые задания из второй и третьей части.

Вариант № 3 (2.3)

Чему равна сумма семи первых членов геометрической прогрессии , если

Решение.

                    

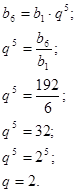
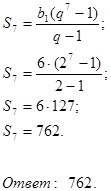
Вариант № 41 (2.2)

Вычислите сумму пяти первых членов геометрической прогрессии , если  а знаменатель  

Решение.

                  

 

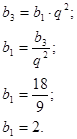
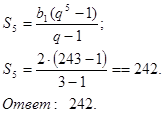
Вариант № 9 (3.3)

          Сумма второго и третьего членов геометрической прогрессии равна 30, а разность четвертого и второго равна  90. Найдите первый член прогрессии.

            

          

Решение.

        

 

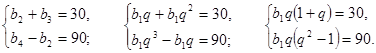
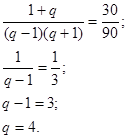
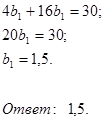
Разбор практико-ориентированных задач.

 

ІІ группа «Эксперты ».  Состав    человек.

Задание: использование прогрессий в разных науках

Представители группы покажут результаты исследования.

 

1. Химия. При повышении температуры по арифметической прогрессии

скорость химических реакций растет по геометрической прогрессии.

2. Геометрия. Вписанные друг в друга правильные треугольники образуют геометрическую прогрессию.

3. Физика. Нейтрон, ударяя по ядру урана, раскалывает его на две части. Получаются два нейтрона. Затем два нейтрона, ударяя по двум ядрам, раскалывает их еще на 4 части и т.д. – это геометрическая прогрессия.

4. Биология.

Известно, что бактерии размножаются делением: одна бактерия делится на две; каждая из этих двух в свою очередь тоже делится на две, и получаютсячетыре бактерии; из этих четырех в результате деления получаются восемь бактерий и т. д. Результат каждого удвоения будем называть поколением. Способность к размножению у бактерий настолько велика, что если бы они негибли от разных причин, а беспрерывно размножались, то за трое суток общая масса потомства одной только бактерии могла бы составить 7500 тонн. Таким громадным количеством бактерий можно было бы заполнить около 375 железнодорожных вагонов.

 

Задача.

Известно, что бактерия в питательной среде через каждые полчаса делится на две. Сколько всего бактерий может образоваться из одной бактерии за 10 часов?

Решение.

Бактерия была одна, следовательно, . Она делится на две, значит, т. к. время деления полчаса, то за 10 часов произойдет 20 делений

и нам нужно найти .

При решении используем формулу  (7).     Примените эту формулу самостоятельно.   У вас должен получиться ответ ….

Ответ:

 

Интенсивность размножения бактерий используют…         в пищевой

промышленности (для приготовления напитков, кисломолочных продуктов, при квашении, солении и др.),   в фармацевтической промышленности (для создания лекарств, вакцин),  в сельском хозяйстве (для приготовления силоса, корма для животных и др.),  в коммунальном  хозяйстве и природоохранных  мероприятиях  (для очистки сточных вод, ликвидации нефтяных пятен).  Еще примеры организмов, которые распространяются в геометрической прогрессий:

МУХИ……          “Потомство пары мух съест мёртвую лошадь также скоро как лев”.   Карл Линней.  

Девятое поколение одной пары мух наполнило бы куб, сторона которого равна 140 км, или же составило бы нить, которой можно опоясать земной шар 40 млрд. раз

ОДУВАНЧИК…….       “Потомство одного одуванчика за 10 лет может   покрыть  пространство  в  15  раз больше суши земного шара”.К. А. Тимирязев.  

ВОРОБЬИ…… Потомство пары птиц величиной с воробья при продолжительности жизни в четыре года может покрыть весь земной шар за 35 лет.  

 

ІІІ группа «Практики» . Состав     человек.

Задание: геометрическая прогрессия в жизни

Представитель группы расскажет о результатах исследования.

 

1. О финансовых пирамидах:

Разберёмся в механизмах этих организаций. Организатор начинает

вовлекать в свою организацию, и говорит, что, если внести указанную плату по указанным адресам по 1 рублю, а затем заплатить ещё по 5 таким же адресам, вычеркнув первый адрес и дописав свой последним, то через некоторое время вы получите уйму денег. Хотя желающих разбогатеть по щучьему веленью немало, но в выигрыше оказываются только учредители такой игры.

Решение:

Дело в том, что число участников увеличивается в 5 раз с каждым кругом. Если пятёрка устроителей подпишет, допустим, 120 человек со своими адресами, то в первом круге участвуют 120 человек, во втором – 600, в третьем – 3 000, …, в десятом – 234 375 000 человек; это намного больше населения страны. Так что участник, включившийся в восьмом или девятом круге, уже ничего не получит.

…

…

…

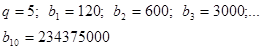
19

 

2. Денежные вклады под проценты — это пример геометрической последовательности. Зная формулы суммы членов геометрической последовательности, можно подсчитывать сумму на вкладе.

 

3. Мощности четырех электромоторов составляют возрастающую геометрическую прогрессию. Мощность первого 5 кВт, а третьего 9,8 кBт. Рассчитать мощность всех четырех электоромоторов.

Решение.        Применяем формулы (5), (7).   

          

 

 

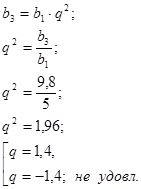
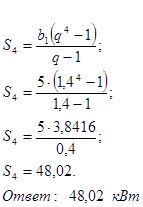
V. Проверка знаний, умений и навыков.

 

1.   (bп) – геометрическая прогрессия. Найдите S4, если b1 = 3, q = –2.   2. Найдите сумму пяти первых членов геометрической прогрессии  1,5; –3; … .

Используйте формулу (7)     Используйте формулы (2), (7)

 

 Проверим работу в парах, в группе 2 + 2, во всем классе.

 

- Кто правильно выполнил всю работу, не допустив ошибок?

- Кто допустил ошибку в одном задании?

- Научились ли мы применять формулы геометрической прогрессии на практике.

- С задачами из каких областей мы с вами встречались?

V. Итоги урока.

В о п р о с ы   у ч а щ и м с я:

– По каким формулам находят сумму первых п членов геометрической прогрессии?

– Какие ограничения накладываются на выражения в формулах?

Вывод:

Сделав анализ задач на прогрессии с практическим содержанием, мы увидели, что прогрессии встречаются при решении задач в медицине, в технике, в живой природе, в науке и в других жизненных ситуациях.

Следовательно,  многим необходим навык применения знаний, связанных с прогрессиями.

Домашнее задание:

Прокомментировать:   п. 28 (с.168 повторить) 

                                       № 650 (а)        Какие формулы мы применим?

                                       № 654 (б)

                                       № 656 (для тех кто хочет знать больше)