Свойства показательной функции

Свойства показательной функции и примеры, графика, таблицы.

Свойства показательной функции и примеры

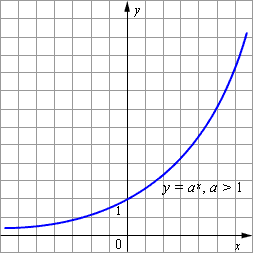
Рис. 1

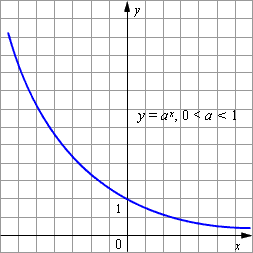
Рис. 2

Таблица

Свойства показательной функции	y = , a > 1	y = , 0< a < 1
1.Область определения функции
2.Область значений функции
3.Промежутки сравнения с единицей	при x > 0, > 1	при x > 0, 0< < 1
	при x < 0, 0< < 1	при x < 0, > 1
4.Чётность, нечётность.	Функция не является ни чётной, ни нечётной (функция общего вида).
5.Монотонность.	монотонно возрастает на R	монотонно убывает на R
6.Экстремумы.	Показательная функция экстремумов не имеет.
7.Асимптота	Ось Ox является горизонтальной асимптотой.
8. При любых действительных значениях x и y;

Пример № 1. (Для нахождения области определения функции). Какие значения аргумента являются допустимыми для функций:

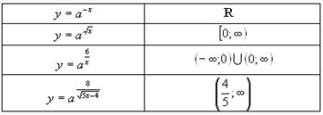
Пример № 2. (Для нахождения области значений функции). На рисунке изображен график функции. Укажите область определения и область значений функции:

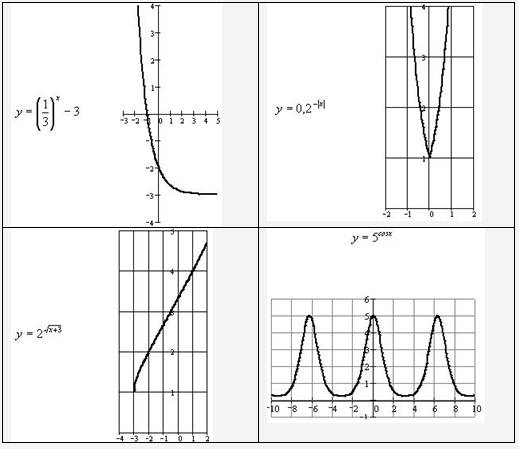
Рис.

Пример № 3. (Для указания промежутков сравнения с единицей). Каждую из следующих степеней сравните с единицей:

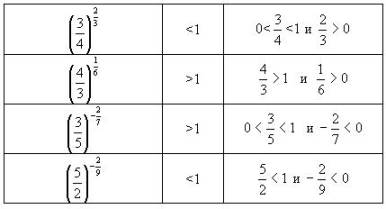
Пример № 4. (Для исследования функции на монотонность). Сравнить по величине действительные числа m и n если:

Таблица. Вывод:

при x < 0	чем больше значение основания степени, тем ближе к оси Ox располагается график показательной функции;
при x = 0	графики показательных функций пересекаются в одной точке (0;1);
при x > 0	чем больше значение основания степени, тем дальше от осиOx располагается график показательной функции.

Таблица. Вывод:

при x < 0	чем меньше значение основания степени, тем дальше от оси Ox располагается график показательной функции;
при x = 0	графики показательных функций пересекаются в одной точке (0;1);
при x > 0	чем меньше значение основания степени, тем ближе к осиOx располагается график показательной функции.

Свойства показательной функции и примеры

Таблица Свойства показательной функции y = , a > 1 y = , 0< a < 1 1

Пример № 1. (Для нахождения области определения функции)

Пример № 3. (Для указания промежутков сравнения с единицей)

Таблица. Вывод: при x < 0 чем больше значение основания степени, тем ближе к оси

Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

02.02.2021