
Технологическая карта по теме «Длина окружности» (мозговой штурм).
Класс: 6
Учебник: Математика: 6 класс: учебник для обучающихся общеобразовательных учреждений. А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. — М.: Вентана–Граф, 2013 [23, с.106].
Тема урока: «Длина окружности»
Тип урока: урок изучения нового.
Цели урока:
Дидактические: изучить формулу длины окружности и площади круга; систематизировать и обобщить знания и умения использования формул при решении задач.
Развивающие: развивать логическое мышление, познавательный интерес, самостоятельность и воображение обучающихся.
Воспитательные: воспитывать умение слушать и вступать в диалог, участвовать в обсуждении проблем, формировать коммуникативную компетенцию обучающихся и уважительное отношение друг к другу, воспитывать интерес к предмету, ответственность и аккуратность.
Владеет: опытом мозгового штурма для поиска выхода из ситуации затруднения; выполнения практической работы, обобщения наблюдений и представления их в математической форме.
Учебные действия, формируемые на уроке:
Предметные:
знает формулу длины окружности,
площади круга, чему равно число ![]() умеет верно использовать в речи термины «длина
окружности», «площадь круга», вычислять длину окружности и площадь круга,
используя знания о приближённых значениях чисел; владеет знанием как вычислять значение числа
умеет верно использовать в речи термины «длина
окружности», «площадь круга», вычислять длину окружности и площадь круга,
используя знания о приближённых значениях чисел; владеет знанием как вычислять значение числа ![]() ;числовое значение числа
;числовое значение числа ![]() .
.
Личностные: умение учащегося устанавливать связи между целью, мотивом учебной деятельности и ее результатом; умение учащегося выдвигать идеи для решения практической задачи; умение организовать собственную деятельность в ходе практической работы в паре.
Регулятивные: умение формулировать собственную познавательную задачу на уроке; определять границы собственного знания и незнания на основе анализа проблемной ситуации; умение планировать деятельность для решения поставленных задач; умение оценивать уровень освоения нового знания.
Коммуникативные: умение сотрудничать с учителем и сверстниками в мозговом штурме, в ходе поиска формулы, анализа обобщения общей исследовательской работы; умение с достаточно полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации; умение обосновать свое мнение в ходе совместного обсуждения; владение монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими нормами родного языка.
Познавательные: умение анализировать два вида задач, записывать с помощью формулы способы их решения; умение описывать смоделированную практическую ситуацию на математический язык с помощью формулы; умение выдвигать идеи для решения и обосновывать их, формулировать выводы на основе наблюдений и решения практической задачи; умение сравнивать две формулы по условию, требованию и применимости к решению.
Методы обучения: метод мозгового штурма.
Средства обучения: круги с прикрепленной к ним ниткой, калькулятор, презентация.
|
Деятельность учителя |
Деятельность учеников |
Планируемые результаты |
|
УУД |
||
|
1.Актуализация знаний (10 мин). 1) Решение задач на нахождение среднего арифметического, квадрата числа, округление чисел. − Найдите среднее арифметическое чисел 15,2; 6 и 0,8; 4; 0,4. − Как находится среднее арифметическое двух чисел? Трех чисел? Нескольких чисел? − Округлите до десятых и выберите слово • 3, 27, а) 3 б) 3,2 в) 3,3 • 23, 34, а) 23,3 б) 23,4 в)23.30 • 0, 185, а) 0, 18 б) 0,2 в) 0.3
− Вычислите и выберите слово
− Выберите слова, которые характеризуют математические свойства понятия: обруч, кольцо (окружность, хорда, радиус) Диск, колесо (круг, центр, диаметр) − Какие опорные слова получили? − Составьте 2 словосочетания из этих слов. Это тема урока. 2) Распознавание диаметра, радиуса окружности по чертежу. Опрос. − Что такое окружность, круг? − Какой отрезок называется радиусом? − Сколько радиусов можно провести в окружности? – Как связаны между собой радиус и диаметр одной окружности? − Найдите по чертежу все радиусы, диаметры.
|
10,55 3,1 Сумму чисел разделить на количество слагаемых.
Длина.
Площадь.
Окружность Круг. Окружность, круг, длина, площадь
Длина окружности, площадь круга.
Отрезок, соединяющий центр окружности с точкой на ней. Диаметр равен двум радиусам.
Радиусы: ОВ, ОА, ОС. Диаметр ВС. |
Коммуникативные: умение выражать свои мысли четко, ясно, в соответствии с поставленным вопросом, осмысливать, составлять словосочетания из данных слов, формулировать тему урока. Познавательные: умение выполнять действия в соответствии с правилом. Регулятивные: умение определять последовательность промежуточных целей с учетом конечного результата. Личностные: умение работать сообща для достижения общей задачи, умение осуществлять самоопределение. |
|
Интерактивные формы и методы. 1) Введение задачи для мозгового штурма − На уроке необычный гость. Слайд. Баба Яга ты, что здесь делаешь? – Летела к лешему, ступа повредилась, починил лохматый. Только сдается мне, что скорость у неё не та стала. Как бы проверить? – Очень просто. Ты пролети круг. Я время замечу. – Как же мой путь измерить? Он же не прямой? Вопрос: как вычислить скорость ступы? 2) Запись предложений детей на доску − Как найти путь круговой траектории? − Какой из предложенных вариантов самый легкий? Самый точный? − Почему? 3) Формулировка темы урока, определение задач собственной деятельности, составление плана работы на уроке. |
Путь разделить на скорость.
По длине и ширине. По длине окружности. По частям, пролетев несколько раз и т.д..
По длине окружности. — Это путь описываемый ступой.
Как вычислить скорость при движении по кругу. Длина окружности |
Коммуникативные: умение формулировать. Познавательные: умение анализировать условие и требования задачи, выдвигать гипотезы в ходе поиска ответа на вопрос с неизвестным условием, анализировать их. Регулятивные: умение поставить собственную учебную задачу на уроке. Личностные: понимание универсальности математических формул не зависящих от несущественных признаков, в данном случае, от круговой или прямолинейной траектории. |
|
2. Открытие нового знания (15 мин). 1) Практическое вычисление числа π в исследовательской работе −Возьмите круг. Измерьте линейкой диаметр. Результат измерений запишите в тетрадь d =… − Обмотайте нитью круг, отметьте точку соединения начала и конца. Выпрямите, измерьте длину окружности. Запишите С − … −Найдите с помощью калькулятора отношение длины окружности к диаметру. Запишите С /d = … − Перенесите результаты измерений в таблицу на доске.
− Почему получились разные значения отношения С к d? Выберем самые разные 10 значений, вычислим среднее арифметическое значение этого отношения. − Какое число получилось? − Математики обозначили это число π (пи) – это отношение длины окружности к ее диаметру. 3 <π < 4. π ≈ 3, 141592653589793238462643….)
2) Вывод формул для вычисления длины окружности и площади круга − Составьте, используя С, d, π, формулу для вычисления длины окружности − Сколько радиусов в диаметре? − Составьте другую формулу. − Для вычисления площади круга используется формула S = πR2. Прочитайте по карточке, расскажите, как она получается (Приложение) 3) Сравнение двух формул − Сравните. Чем похожи? Чем отличаются? − Почему для вычисления длины окружности выражение 2πR, для вычисления площади круга πR2? 4) Задача мозгового штурма: решение, выводы−рациональное «зерно» каждой идеи − Как найти траекторию движения ступы? − Что для этого надо знать? − Давайте вычислим, если радиус равен 50 метрам,100 метрам. − Какова скорость ступы, если полет по кругу с диаметром 100 м длится 4 минуты. |
Выполняют практическую работу.
Из картона выполнены круги разного диаметра, к которым прикреплена нить, предназначенная для измерения длины окружности.
Ребята заполняют таблицу со значениями С, d, найденными дома, на доске и в тетради. При подсчёте используется калькулятор. Дети работают в паре.
~3,14…… 3,14
Работа в паре. Запись на доске. С =πd d = 2R
С = 2πR
− Длина окружности измеряется в линейных единицах, площадь измеряется в квадратных единицах.
− По формуле С = 2πR
157 м 314 м 78,5 м в минуту. |
Коммуникативные: умение записывать информацию, полученную практически, в таблицу, с помощью математических знаков. Умение записывать правило вычисления длины окружности через математические символы, отвлекаться от несущественных признаков. Познавательные: поиск причинно−следственных связей для объяснения ответов, умение анализировать результаты таблицы, обобщать, умение сравнивать две формулы по названиям, по компонентам, входящим в эту формулу, по выполняемым действиям. Регулятивные: умение организовать собственную самостоятельную работу в группе для вычисления общего результата. Личностные: умение чувствовать сопричастность к результатам работы в группе, умение переживать радость от открытия нового, от решения проблемной ситуации, поставленной в начале урока. |
|
3. Первичное закрепление знаний (10 мин). Чтение текста учебника. Вывод формул. Формулы. − Какая у нас получилась формула, сверьте. 1) решение задач на прямое применение формул − Вычислите длину окружности и площадь кругов, лежащих на ваших партах по формулам. − Работа в группах (составление задач на применение формул длины окружности и площади круга, радиуса или диаметра, запись на листочках.) Анализ составленных задач, классификация их по типам: задачи на применение формулы, задачи с изменением условия, задачи на вывод из формулы величины, занимательные задачи, задачи на построение. 2) решение задач на вычисление радиуса или диаметра при известной длине окружности 3) Проверка. Выделение интересных задач.
3. Обобщение − Какие две формулы узнали? Какие? Выразите через радиус. − Чем они похожи? Чем отличаются? − Как их запомнить? 4. Дополнительная занимательная задача «люки» Почему крышки канализационных люков делают круглыми, а не квадратными? |
Работа с текстом учебника
Работа у доски и в тетрадях с комментарием. Введение числовых значений радиуса, диаметра, длины окружности.
Мозговой штурм в группе. Составление 4 стопок. Обмен групп заданиями. Выбор задач из стопки. Выполнение и взаимопроверка с комментарием по критериям, определенным заранее: оформление, правильность, правильность единиц измерения.
Длины окружности и площади круга. Содержат число пи, число 2, радиус. Для длины окружности на 2 умножаем, для площади круга возводим во вторую степень.
Круг имеет наименьшую площадь |
Коммуникативные: умение составлять текст задачи формулировать четко условия и требование задачи, уметь оформить свои мысли в устной и письменной форме. Познавательные: умение анализировать условие задачи, составлять новую с соответствии с требованиями задачи, решать ее по найденному правилу и проверять свое решение. Регулятивные: умение выполнять самопроверку решенной задачи, определять последовательность действий для достижения результата. Личностные: умение составлять интересную задачу для решения в группе, потрудиться ради достижения общей цели. Умение принять успешность другого человека, порадоваться за него. |
|
1. Рефлексия (5 мин). Давайте вспомним, что сегодня на уроке − Повторили… − Узнали… − Сумел ли ты получить новые знания? − Ты сумел показать свои знания? − Какие задачи были самыми интересными? − Какая идея мозгового штурма оказалась верной? |
Среднее арифметическое, части круга, окружности. Две формулы: длины окружности и площади круга. Составленные самими |
Регулятивные: умения проанализировать последовательность действий в достижении цели на основе ретроспективной оценки. Личностные: умение осуществлять самооценку на основе критериев успешности учебной деятельности. |
|
5. Домашнее задание (5 мин). Поскольку математика тесно связана с жизнью, задание будет творческое. Может вы увидите окружность или круг в колесе, может в цирке, у мамы на кухне и т.д. Придумайте и составьте задачу по теме «Длина окружности. Площадь круга»» и сделайте красочный рисунок к задаче. |
Дети записывают. |
Работа по карточкам.
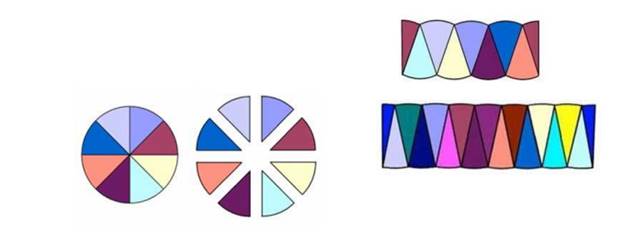
Если
разрезать круг на секторы и приложить их к друг другу, как показано на рисунке,
то получившаяся фигура при увеличении количества секторов становится очень
похожей на прямоугольник. Значит, и её площадь можно найти по формуле площади
прямоугольника. Ширина нашего прямоугольника равна радиусу окружности (R), а
длина прямоугольника равна половине длины окружности (C/2). Площадь
прямоугольника равна произведению длины на ширину, т. е. S=RC/2, а т.к. C=2πR,
значит ![]() или
S=πR2. Так как прямоугольник был составлен из частей круга, то
их площади равны. Значит, площадь круга равна: S= πR2
или
S=πR2. Так как прямоугольник был составлен из частей круга, то
их площади равны. Значит, площадь круга равна: S= πR2
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.