
Урок4. Решение задач.
Подготовка к контрольной работе
|
Цели деятельности учителя |
Совершенствовать навыки решения задач; создать условия для подготовки учащихся к предстоящей контрольной работе |
|
|
Термины и понятия |
Треугольник, противолежащий угол, сторона, неравенство треугольника |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Умеют работать с геометрическим текстом, точно и грамотно
выражать свои мысли в устной и письменной речи |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев. Регулятивные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем. Коммуникативные: умеют работать в сотрудничестве с учителем, аргументировать и отстаивать свою точку зрения. Личностные: проявляют креативность мышления, инициативу, находчивость, активность при решении геометрических задач |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные ресурсы |
• Задания для фронтальной, самостоятельной работы. • Чертежи к задачам |
|
|
I этап. Актуализация опорных знаний учащихся |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Проверить уровень сформированности теоретических знаний |
(Ф/И) 1. Доказательство теоремы о соотношениях между сторонами и углами треугольника и теоремы о неравенстве треугольника. (Выполняют учащиеся у доски и за первыми партами – на листках. По окончании работы листки собрать и выслушать ответы учеников.) 2. Фронтальная работа с классом: 1) Ответить на вопросы 1–9 на с. 88. 2) Устно решить задачу. Существует ли треугольник со
сторонами 4 м, 5 м и 8 м; со сторонами 6 см, 12 см и 3 см; со сторонами 9 дм,
|
|
|
II этап. Решение задач |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Совершенствовать |
(Ф/И) 1. Решение задач по готовым чертежам. 1) Может ли длина АВ быть равной 27 см?
Рис. 1 2) Дано: R1 = 5 cм, R2 = 4 см. Каким может быть расстояние от точки О1 до точки О2?
Рис. 2 3) Доказать:ÐABС>ÐC. 4) Сравнить АС и ВС.
Рис. 3 Рис. 4 5) Доказать: ВС<ВМ<ВА. 6) Доказать: BD + DС>AD.
Рис. 5 Рис. 6 2. Решение задачи (один ученик решает у доски, остальные – в тетрадях). Дано: отрезок ЕK – биссектриса треугольника DEC. Доказать:KС<ЕС.
Рис. 7 Доказательство: ÐЕKС – внешний угол ∆DKE, значит, он больше Ð1, следовательно, ÐEKС>Ð2 (Ð1 = Ð2, так как ЕK – |
|
|
III этап. Самостоятельная работа |
||
|
Цель деятельности |
Задание для самостоятельной работы |
|
|
Проверить умение применять полученные знания при решении задач |
(И) Выполняют задания самостоятельной работы (см. Ресурсный материал) |
|
|
IV этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) – Какие теоремы использовались при решении задач? – Оцените свою работу на уроке. – Какие трудности возникли у вас при решении задач? |
(И) Домашнее задание: подготовиться к контрольной работе, повторив материал пунктов 17–34; решить задачи № 244, 252, 297 |
|
Ресурсный материал
Самостоятельная работа
1. Дано:ÐBAE = 112°, ÐDBF = 68°, ВС = 9 см. 2. Дано:ÐCBM = ÐACF, РАВС = 34 см, ВС = 12 см.
Найти: АС. Найти: АВ.
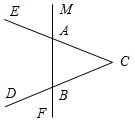
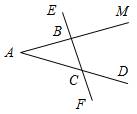
Рис. 1 Рис. 2
3. Одна из сторон тупоугольного равнобедренного треугольника на 17 см меньше другой. Найдите стороны этого треугольника, если его периметр равен 77 см.
4. В равнобедренном треугольнике биссектрисы углов при основании образуют при пересечении угол, равный 52°. Найдите угол при вершине этого треугольника.
5. В треугольнике ABCÐB = 70°, ÐC = 60°. Сравните стороны треугольника.
6. Дано:ÐC = 90°, ÐB = 27°, CD – высота ∆ABC, СK – биссектриса ∆АВС.
Найти:ÐDCK.
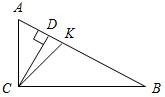
Рис. 3
Ответы и указания к задачам для самопроверки:
1. АС = 9 см, так как ∆АВС – равнобедренный (ÐABC = ÐBAС).
2. АВ = 11 см, так как ∆АВС – равнобедренный с основанием ВС (ÐABC = ÐACB).
3. 20 см, 20 см, 37 см.
4. Решение (см. рис. 4):
ÐAOC ≠ 52°, тогда Ð1 + Ð 2 = 128° и Ð3 + Ð4 = 128°, a ÐВАС + ÐВСА = 256°, чего быть не может, значит, ÐАОС1 = 52°, тогда Ð1 + Ð2 = 52°, Ð3 + Ð4 = 52°, a ÐВAC + ÐВСА = 104°, значит, ÐАВC = 76°.
Ответ: ÐABC = 76°.
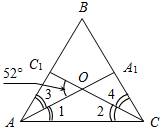
Рис. 4
5. ÐВ = 70°, ÐC = 60°, тогда ÐA = 50°. Следовательно, по теореме о соотношениях между сторонами и углами треугольника, ВС<АВ <АС.
Ответ: ВС<АВ<АС.
6. ÐACK = 45°, ÐBAC = 63°, тогда ÐАСD = 27°, ÐDCK = ÐАСK – ÐАСD = 45° – 27°= 18°.
Ответ: ÐDCK = 18°.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.