
Технологическая карта урока №12
Тема урока Формулы для нахождения площади треугольника
Тип урока Урок изучения нового материала.
Формируемые результаты
Предметные: формировать
умение доказывать и применять фор- мулу для нахождения площади
треугольника 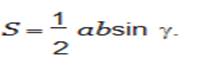
Личностные: формировать интерес к изучению темы и желание применять приобретённые знания и умения.
Метапредметные: формировать умение устанавливать причинно- следственные связи, строить логическое рассуждение, умозаклю- чение (индуктивное, дедуктивное и по аналогии) и делать выводы.
Планируемые результаты
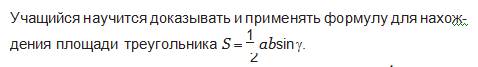
Основные понятия
![]()
Организационная структура урока
|
Этапы проведения урока |
Форма органи- зации УД |
Задания для учащихся, выполнение которых приведёт к достижению планируемых результатов |
||||||
|
Учебник |
Рабочая тетрадь № 1 |
Дидактические материалы |
||||||
|
1 |
2 |
3 |
4 |
5 |
||||
|
1. Организационный этап |
||||||||
|
2. Постановка формируемых результатов урока. Мотивация учебной деятель- ности учащихся |
||||||||
|
3. Проверка домашнего задания |
||||||||
|
4. Актуализа- ция знаний |
Ф |
Устно. № 1. Как вычислить площадь треугольника, если известны сторона треугольника и высота, проведённая к этой стороне? № 2. Как вычислить площадь прямоугольного треуголь- ника, если известны его катеты? |
||||||
|
5. Изучение нового мате- риала |
Ф |
Теоретический материал § 5 (теорема 5.1, задачи 1, 2) |
|
|
||||
|
6. Первичное закрепление |
Ф |
№ 132, 134, 135, 137 |
|
|
||||
|
нового мате- |
|
|
||||||
|
И |
|
№ 79, 80 |
№ 51 |
|||||
|
риала |
||||||||
|
7. Повторение |
И |
№ 170 |
|
|
||||
|
8. Итоги урока |
|
Вопрос 1, с. 38 |
|
|
||||
|
9. Информа- ция о домаш- |
|
§ 5, № 133, 136, 171 |
|
|
||||
|
нем задании |
|
|||||||
|
||||||||
Методические комментарии
Теоретический материал данного параграфа предоставляет ряд формул для нахождения площади треугольника по разным исходным данным. Эти формулы вместе с изученными в предыдущих параграфах теоремами косинусов и синусов существенно расширяют математический аппарат, которым учащиеся могут пользоваться для нахождения элементов и характеристик треугольника (стороны, углы, периметр, радиус вписанной и опи- санной окружности, площадь). Поэтому задачи данного параграфа требуют от учащихся в первую очередь анализа набора исходных данных и выбора того аппарата, с помощью которого по имеющимся исходным данным мож- но за один или несколько шагов найти требуемые неизвестные величины.
![]()
и формула Герона позволяют находить радиусы описанной и вписанной окружностей треугольника по его сторонам. Это иллюстрирует пример, разобранный в параграфе.
В зависимости от возможностей класса можно предложить другое решение ключевой задачи 2 параграфа. Провести через каждую вершину четырёхугольника прямую, параллельную соответствующей диагонали. Далее показать, что площадь образовавшегося параллелограмма в два раза больше площади данного многоугольника, а затем воспользоваться ключевой задачей 1
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.