
Урок 31. Решение задач
на применение признаков параллельности прямых
|
Цели деятельности учителя |
Создать условия для закрепления и систематизации изученного материала, обучения применению признаков параллельности прямых при решении задач; способствовать развитию логического мышления учащихся; содействовать воспитанию аккуратности при построении чертежей на доске и в тетрадях |
|||
|
Термины и понятия |
Параллельные прямые, накрест лежащие углы, соответственные углы, односторонние углы |
|||
|
Планируемые результаты |
||||
|
Предметные умения |
Универсальные учебные действия |
|||
|
Владеют геометрическим языком, умеют его использовать для описания предметов окружающего мира, имеют достаточно высокий уровень пространственных представлений и изобразительных умений, владеют навыками геометрических построений |
Познавательные: умеют устанавливать причинно-следственные связи, строить логическое рассуждение, делать умозаключения и выводы. Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками, работать самостоятельно. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
|||
|
Организация пространства |
||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|||
|
Образовательные |
• Чертежи к задачам. • Задания для самостоятельной работы |
|||
|
I этап. Актуализация опорных знаний учащихся |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Систематизировать |
(Ф/И) 1. Проверить правильность выполнения домашнего задания. 2. Провести теоретический опрос по признакам параллельности прямых. 3. Решить задачи по готовым чертежам (устно). 1) Докажите, чтоа || b. 2) Докажите, чтоа || с. 3)Докажите, чтоа || b и т || п, если Ð1 = Ð2 = Ð3.
Рис. 1 Рис. 2 Рис. 3 4) Дано:Ð1 = 83°, Ð2 больше Ð1 на 14°. 5) Дано:Ð2 = 114°, Ð1 меньше Ð2 на 20°. Параллельны ли прямые MN и AB? Параллельны ли прямые СЕ и AB?
Рис. 4 Рис. 5
|
|||
|
II этап. Решение задач |
||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
||
|
Совершенствовать |
(Ф/И) Организует деятельность учащихся. 1. Решить задачу № 190 по рисунку 109 (на доске и в тетрадях). 2. Решить задачу № 213 по рисунку 121 (на доске и в тетрадях). 3. Решить задачу № 215 по рисунку 122 (устно). Указание: рисунок 122 заранее
перенести |
Дано:АВ = ВС, АD = DЕ, ÐС = 70°, ÐЕАС = 35°. Доказать:DЕ || АС.
Рис. 6 Доказательство: 1) Так как АВ = ВС, то ÐА = ÐС = 70° (свойство равнобедренного треугольника). 2) Так как ÐЕАС = 35°, ÐА = 70°, то ÐDАЕ = 35°. 3) Так как DАDЕ – равнобедренный, то ÐDАЕ = ÐDЕА = 35° (по свойству). 4) ÐDЕА = ÐЕАС = 35°. ÐDЕА и ÐЕАС – накрест лежащие при прямых DЕ и АС и секущей АЕ. DЕ || АС, что и требовалось доказать.
Дано: СЕ = ЕD, ВЕ = EF, KE || AD. Доказать: KE || BC.
Рис. 7 Доказательство: 1) Рассмотрим DВСF и DFDЕ. ВЕ = EF (по усл.), СЕ = ЕD (по
усл.), Ð1 = Ð2 2) ÐСВЕ = ÐDFЕ – накрест лежащие
при прямых BC и AD и секущей ВF, 3) KE || AD (по усл.), BC || AD (из п. 2), тогда KE || BC (свойство параллельных прямых), что и требовалось доказать |
||
|
III этап. Самостоятельная работа |
||||
|
Цель деятельности |
Задания для самостоятельной работы |
|||
|
Проверить умение применять признаки параллельности при решении задач |
(И) Самостоятельная работа выполнятеся на листках и сдается на проверку учителю (см. Ресурсный материал) |
|||
|
IV этап. Итоги урока. Рефлексия |
||||
|
Деятельность учителя |
Деятельность учащихся |
|||
|
(Ф/И) – Оцените свою работу на уроке. – Задайте три вопроса по теме |
(И) Домашнее задание: повторить материал пунктов 24–26; решить задачи № 214, 216 |
|||
Ресурсный материал
Самостоятельная работа
Вариант I
1. Параллельны ли прямые d и е, изображенные на рисунке 1?
2. На рисунке 2 точка О– середина отрезков EL и KF. Докажите, что EF || KL.
Вариант II
1. Параллельны ли прямые m и n, изображенные на рисунке 3?
2. На рисунке 4 точка F – середина отрезков MО и NP. Докажите, что MN || PO.
Вариант III
1. Какие из прямых, изображенных на рисунке 5(m, n и p), являются параллельными? Ответ обоснуйте.
2. В равнобедренных треугольниках СDЕ и FPK, изображенных на рисунке 6, Ð1 = Ð2. Докажите, что СD || PF.
Вариант IV
1. На рисунке 7 МD = NP, Ð1 = Ð2. Докажите, что MN || DP.
2. В равнобедренных треугольниках АВС и DЕF, изображенных на рисунке 8, Ð1 = Ð2. Докажите, что AB || EF.
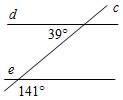
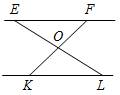
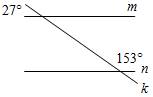
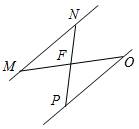
Рис. 1 Рис. 2 Рис. 3 Рис. 4
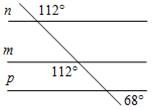
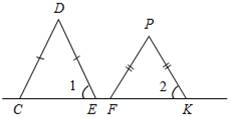
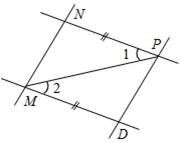
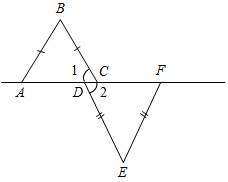
Рис. 5 Рис. 6 Рис. 7 Рис. 8
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.