
Урок 21. Задачи на построение. Окружность
|
Цель деятельности учителя |
Создать условия для систематизации знаний об окружности и ее элементах, для отработки навыков решения задач по данной теме |
||
|
Термины и понятия |
Окружность, центр, радиус, диаметр, хорда |
||
|
Планируемые результаты |
|||
|
Предметные умения |
Универсальные учебные действия |
||
|
Умеют формулировать определение окружности, объяснять, что такое центр, радиус, диаметр, хорда окружности |
Познавательные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем, устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение. Регулятивные: понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют познавательный интерес к изучению предмета |
||
|
Организация пространства |
|||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
||
|
Образовательные |
• Задания для теста |
||
|
I этап. Актуализация опорных знаний учащихся |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Проверить правильность выполнения домашнего задания |
(Ф/И) 1. Сообщить результаты самостоятельной работы. 2. Проверить правильность выполнения домашнего задания |
||
|
II этап. Учебно-познавательная деятельность |
|||
|
Цель деятельности |
Задания для самостоятельной работы |
||
|
Ввести понятия окружности и ее элементов |
(И) Понятие окружности и ее элементов вводится в курсе математики пятого класса, поэтому изучение нового материала можно организовать следующим образом: 1. Прочитать самостоятельно § 21. 2. Выполнить задания теста (см. Ресурсный материал). (На каждую парту раздаются листки с тестовым заданием. Учитель читает задание, учащиеся предлагают верный ответ.) |
||
|
III этап. Закрепление изученного материала |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Отработать навыки решения задач по изученной теме |
(Ф/И) 1. Решить задачу № 143 (устно). 2. Решить задачу № 144 на доске и в тетрадях. 3. Решить задачу № 146 на доске и в тетрадях. 4. Решить задачу № 147 на доске и в тетрадях. Указание: рекомендовать
учащимся после изображения окружности начертить прямой угол с вершиной |
||
|
IV этап. Самостоятельная работа |
|||
|
Цель деятельности |
Задания для самостоятельной работы |
||
|
Проверить уровень усвоения теоретического материала и умения его применять при решении задач |
(И) Вариант I Отрезки KМ и ЕF являются диаметрами окружности с центром О. Докажите, что: а) ÐFEM = ÐKМЕ; б) отрезки KЕ и МF равны. Вариант II Отрезки МЕ и РK являются диаметрами окружности с центром О. Докажите, что: а) ÐEMР = ÐМРK; б) отрезки МK и РЕ равны. Вариант III В окружности с центром Опроведены диаметр АС и радиус ОВ так, что хорда ВС равна радиусу. Найти ÐАОВ, если ÐВСО = 60°. Вариант IV В окружности с центром О проведены хорды АВ и СD. Докажите, что АВ = СD, если ÐАОС = ÐВОD |
||
|
V этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
(Ф/И) – Дайте определение окружности. – Перечислите все элементы окружности. – Составьте синквейн к уроку |
(И) Домашнее задание: изучить п. 21 из § 4; ответить на вопрос 16 на с. 49; решить задачи № 145, 162; принести на следующий урок циркули и линейки. Дополнительная задача: АВ и CD – два диаметра окружности с центром в точке О. Луч ОЕ – биссектриса угла АОС. ОЕ пересекает окружность в точке K, причем KЕ = KО. Периметр треугольника KСО в три раза больше радиуса окружности. Докажите, что точки Е, А, С и О лежат на одной окружности |
||
Ресурсный материал
Тест
1) Вычеркнуть ненужные слова текста в скобках.
а) Окружность – это (абстрактная, геометрическая, плоская) фигура, состоящая из (множества, всех) точек, расположенных на (одинаковом, заданном) расстоянии от (некоторой, центральной) точки.
б) Радиусом окружности называется (линия, прямая, отрезок), соединяющая центр окружности с (заданной, какой-либо) точкой окружности.
2) Закончить определение: диаметр окружности – это...
а) два радиуса, лежащие на одной прямой;
б) хорда, проходящая через центр окружности;
в) прямая, проходящая через две точки и центр окружности.
3) Закончить определение: центр окружности – это...
а) точка, куда ставится ножка циркуля при начертании окружности;
б) середина окружности;
в) точка, равноудаленная от всех точек окружности.
4) Закончить определение: дуга окружности – это...
а) часть окружности, выделенная точками;
б) часть окружности, ограниченная двумя точками;
в) часть окружности, ограниченная хордой.
5) Определить, на сколько дуг делят окружность две точки, лежащие на окружности:
а) на одну; б) на две.
6) Как изображается хорда на чертеже окружности? Выбрать правильный ответ:
а) прямой линией;
б) дугой окружности;
в) отрезком с концами, лежащими на окружности.
7) Как называется отрезок, соединяющий центр окружности с любой точкой окружности? Выбрать правильный ответ:
а) длина окружности;
б) радиус окружности;
в) половина диаметра окружности.
8) Найти на рисунке:
а) хорду (рис. 1);
б) диаметр (рис. 2).
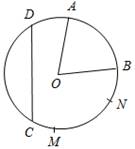
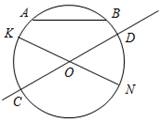
Рис. 1 Рис. 2
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.