
Урок 51. Решение задач
|
Цель деятельности учителя |
Создать условия для обучения применению признаков равенства прямоугольных треугольников и их свойств при решении задач, для выработки умения решать задачи; способствовать развитию умения логически мыслить |
|
|
Термины и понятия |
Треугольник, противолежащий угол, катеты, гипотенуза |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Умеют применять изученные понятия, методы для решения задач |
Познавательные: умеют устанавливать причинно-следственные связи, строить логическое рассуждение, делать умозаключения и выводы; понимают и используют математические средства наглядности. Регулятивные: осуществляют самоконтроль и взаимоконтроль. Коммуникативные: умеют работать в сотрудничестве с учителем, в парах, аргументировать и отстаивать свою точку зрения. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); парная (П); индивидуальная (И) |
|
|
Образовательные |
• Чертежи к задачам. • Задания для самостоятельной работы |
|
|
I этап. Актуализация опорных знаний учащихся |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Систематизировать |
(Ф/И) 1. Ответить на вопросы учащихся по домашнему заданию. 2. Сформулировать свойства прямоугольных треугольников. 3. Сформулировать признаки равенства прямоугольных треугольников. 4. Устно решить задачи по готовым чертежам. 1) На рисунке 1 ÐВ = ÐС =90°; Ð1 = Ð2. Докажите, что АВ = СD. 2) На рисунке 2 АВ = СD; ВС = АD, ÐАFВ = ÐСЕD = 90°. Докажите, что BF = ED; АF = EC. 3) На рисунке 3 Ð1 = Ð2 = 90°, АВ = DС. Докажите, что ВС = АD. 4) На рисунке 4 АН и А1Н1 – высоты треугольников АВС и А1В1С1; АС = А1С1; Ð1 = Ð2; АН = А1Н1. Докажите, что ∆АВС = ∆А1В1С1.
Рис. 1 Рис. 2 Рис. 3
Рис. 4 |
|
|
II этап. Решение задач |
||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
Совершенствовать |
(Ф/И) Организует деятельность учащихся. 1. Решить задачу № 263 на доске и в тетрадях. 2. Решить задачу № 267 на доске и в тетрадях. (П) 3. Решить задачи по готовым чертежам. 1) Доказать: ВС^CD.
Рис. 5 2) Найти:ÐАСЕ.
Рис. 6 3) Дано: ВН = 4 см. Найти: АН.
Рис. 7 4) Дано: АВ || CD. Найти: углы ∆CDO.
Рис. 8 5) Дано: О – общая середина АВ и CD, АВ^CD. Доказать: АС = DB.
Рис. 9 6) Доказать: МС – медиана ∆KMN.
Рис. 10 7) Дано: BD – биссектриса ÐАВС. Доказать: DB – биссектриса ÐADC.
Рис. 11 8) Дано: ВМ = 5 см. Найти: ME.
Рис. 12 |
№ 263. Дано:DАВС – равнобедренный, АВ
= АС; Найти:ÐА, ÐВ, ÐС.
Рис. 13 Решение: 1) По свойству смежных углов, 180° – 140° = ÐСМВ1. ÐСМВ1 = 40°, тогда ÐВ1СМ (ВСС1) = 90° – 40° = 50°. 2) ÐА = 90° – ÐВ1СС1 = 90° – 50° = 40°. 3) По свойству углов в треугольнике, ÐВ + ÐС = 180° – ÐА, ÐВ + ÐС = 180° – 40° = 140°. Так как ÐВ = ÐС (АВ = АС), то ÐВ = 70°, ÐС = 70°. Ответ: 40°, 70°, 70°. № 267. Дано:DAВC и DA1В1C1, СС2, ВВ2, С1М1,
В1N1 – высоты; Доказать:DAВC = DA1В1C1.
Рис. 14 Доказательство: 1) Рассмотрим DВ2ВС и DN1В1С1. ВС = В1C1 (по усл.), ВВ2 = В1N1 (по усл.), следовательно, DВ2ВС = DN1В1С1 (по гипотенузе и катету), тогда ÐС = ÐС1 (по определению равных треугольников). 2) Рассмотрим DС2ВС и DМ1В1С1. ВС = В1C1 (по усл.), СС2 = С1М1
(по усл.), следовательно, DС2ВС = DМ1В1С1, 3) Рассмотрим DAВC и DA1В1C1. ВС = В1C1 (по
усл.), |
|
III этап. Самостоятельная работа |
||
|
Цель деятельности |
Задания для самостоятельной работы |
|
|
Проверить уровень |
(И) Учащиеся выполняют задания самостоятельной работы (см. Ресурсный материал) |
|
|
IV этап. Итог урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) – Перечислите свойства прямоугольного треугольника, которые применили при решении задач самостоятельной работы. – Оцените свою работу и работу своего напарника |
(И) Домашнее задание:
повторить п. 30–36, подготовиться |
|
Ресурсный материал
Самостоятельная работа
Вариант I
1. На рисунке 1 АD = DС; ЕD = DF; Ð1 = Ð2 = 90°. Докажите,что треугольник АВС равнобедренный.
2. Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего катета равна 18 см. Найдите гипотенузу и меньший катет.
Вариант II
1. На рисунке 2 Ð1 = Ð2, Ð3 = Ð4 = 90°; ВD = DС. Докажите, что треугольник АВС равнобедренный.
2. Один из острых углов прямоугольного треугольника в два раза меньше другого, а разность гипотенузы и меньшего катета равна 15 см. Найдите гипотенузу и меньший катет.
Вариант III
(для более подготовленных учащихся)
1. Через середину отрезка АВ проведена прямая а. Из точек А и В к прямой а проведены перпендикуляры АС и ВD. Докажите, что АС = ВD.
2. В прямоугольном треугольнике СDЕ с прямым углом Е проведена высота EF. Найдите CF и FD, если СD = 18 см, а ÐDСЕ = 30°.
Вариант IV
(для более подготовленных учащихся)
1. Из точки М биссектрисы неразвернутого угла О проведены перпендикуляры МА и МВ к сторонам этого угла. Докажите, что МА = МВ.
2. В прямоугольном треугольнике АВС с гипотенузой АВ и ÐА = 60° проведена высота СН. Найдите ВН, если АН = 6 см.
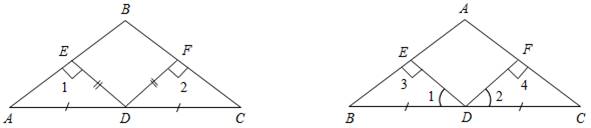
Рис. 1 Рис. 2
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.