
Урок 20. Решение задач
|
Цели деятельности учителя |
Создать условия для организации и проведения повторения и закрепления изученного материала в ходе решения задач, обучения учащихся умению применять изученные теоремы при решении задач; способствовать развитию логического мышления |
|||
|
Термины и понятия |
Треугольник, углы, стороны, признаки равенства |
|||
|
Планируемые результаты |
||||
|
Предметные умения |
Универсальные учебные действия |
|||
|
Умеют работать с геометрическим текстом (анализировать его, извлекать необходимую информацию) |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий; умеют устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение. Регулятивные: понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют познавательный интерес к изучению предмета |
|||
|
Организация пространства |
||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|||
|
Образовательные |
• Задания для самостоятельной работы |
|||
|
I этап. Актуализация опорных знаний учащихся |
||||
|
Цель деятельности |
Задание для контрольной работы |
|||
|
Систематизировать |
(Ф/И) 1. Проверка выполнения домашнего задания. 2. Теоретический опрос. 3. Самостоятельная работа на 10–15 минут (см. Ресурсный
материал). Учащиеся решают работу на листках |
|||
|
II этап. Решение задач |
||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
||
|
Совершенствовать |
(Ф/И) 1. Организовать решение № 139 2. Организовать решение № 169 Рассказать учащимся о способе измерения ширины озера(отрезка АВ)
по заранее изготовленной таблице: «Чтобы измерить на местности расстояние
между двумя точками А и В, из которых одна (точка А)
недоступна, провешивают направление отрезка АВ и на его продолжении
отмеряют на земле произвольный отрезок ВС. Выбирают на местности точку
О, из которой видна точка А и можно пройти к точкам В и С.
Провешивают прямые ВОЕ и СОD, отмеряют на местности DО = ОС и
ОЕ = Тогда FE равно искомому расстоянию. Расстояние FE измеряют на земле с помощью рулетки». 3. Организовать решение задачи |
№ 139. Дано:АВ = CD, AD = BC, BE – биссектриса ÐАВС, DF – биссектриса DADC. Доказать: 1) ÐАВЕ = ÐADF; 2) DАВЕ = DCDF.
Рис. 1 Доказательство: 1) Рассмотрим DАВС и DCDA. АВ
= CD (по усл.), BC = AD (по усл.), 2) ÐАВЕ = ÐADF = 3) Рассмотрим DАВЕ и DСDF: АВ = CD (по усл.), ÐВАС = ÐDCA (из п. 1). Ð1 = Ð2 (из пп. 1 и 2), таким образом, DАВЕ = DСDF (по стороне и двум прилежащим углам). № 176. Дано:DАВС и DА1В1С1, АВ = А1В1, АС
= А1С1, АМ = А1М1;
АМ, А1М1 – Доказать:DАВС = DА1В1С1.
Рис. 2 Доказательство: 1) Сделаем дополнительное построение: проведем АМ и А1М1
за точки 2) Рассмотрим DАМС и DBMD. AM = MD (по постр.), BM = MC (по усл.), Ð1 = Ð2 (вертик.), DАМС = DBMD (по
двум сторонам и углу между ними), тогда АС = BD (по определению
равных треугольников), так как 3) Рассмотрим DABD и DA1B1D1. АВ = А1В1 (по усл.), AD = A1D1 (так как АМ = А1М1), BD = B1D1
(из п. 2); таким образом, DABD = DA1B1D1 Так как ВМ = B1M1, то ВС = В1С1 (ВС = 2ВМ; В1С1 =2B1М1). 4) Рассмотрим DАВС и DА1В1С1. АВ = А1В1 (по усл.), АС = А1С1 (по усл.), ВС = В1С1 (из п. 3). Таким образом, DАВС = DА1В1С1 (по трем сторонам), что и требовалось доказать |
||
|
III этап. Итоги урока. Рефлексия |
||||
|
Деятельность учителя |
Деятельность учащихся |
|||
|
(Ф/И) – Перечислите признаки равенства треугольников. – Поразмышляйте на тему «Как бы мы доказывали равенство треугольников, если бы не знали признаков их равенства?» |
(И) Домашнее задание: повторить пункты 16–20 из § 2 и 3; решить задачи № 140, 172. Дополнительная задача: Два равнобедренных треугольника АВС и ADC имеют общее основание АС. Вершины В и D расположены по разные стороны от АС. Точка Е лежит на отрезке BD, но не лежит на отрезке АС. Докажите, что ÐEAC = ÐАСЕ |
|||
Ресурсный материал
Самостоятельная работа
 Вариант I
Вариант I
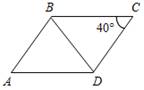
1. Дано: АВ = CD, BC = DA, ÐС = 40°.
Доказать: ∆ABD = ∆CDB.
Найти:ÐA.
2. На боковых сторонах равнобедренного треугольника АВС отложены равные отрезки ВМ и BN. BD – медиана треугольника.
Докажите, что MD = ND.
Вариант II
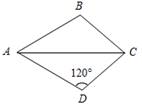 1. Дано:AD = AB, CD = CB, ÐD = 120°.
1. Дано:AD = AB, CD = CB, ÐD = 120°.
Доказать: ∆DAC = ∆BAC.
Найти:ÐВ.
2. На боковых сторонах равнобедренного треугольника ABC отложены равные отрезки ВМ и BN. BD – высота треугольника.
Докажите, что MD = ND.
Самостоятельная работа
 Вариант I
Вариант I
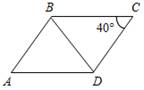
1. Дано: АВ = CD, BC = DA, ÐС = 40°.
Доказать: ∆ABD = ∆CDB.
Найти:ÐA.
2. На боковых сторонах равнобедренного треугольника АВС отложены равные отрезки ВМ и BN. BD – медиана треугольника.
Докажите, что MD = ND.
Вариант II
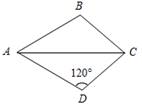 1. Дано:AD = AB, CD = CB, ÐD = 120°.
1. Дано:AD = AB, CD = CB, ÐD = 120°.
Доказать: ∆DAC = ∆BAC.
Найти:ÐВ.
2. На боковых сторонах равнобедренного треугольника ABC отложены равные отрезки ВМ и BN. BD – высота треугольника.
Докажите, что MD = ND.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.