
Поурочное
отс
планирование
скпняя школя
8 класс
КАРТЫ УРОКОВ
ПО УЧЕБНИКУ Л. С. АТАНАСЯНА, В. Ф. БУТУЗОВА, С. Б. КАДОМЦЕВА,
э. г. позняп, и. и. Юдиной
Издательство «УЧИТЕЛЬ»
ИЗДАТЕЛЬСТВО «УЧИТЕЛЬ»
8 класс
Технологические карты уроков по учебнику
Л. С. Атанасяна, В. Ф. Бутузова, С Б. Кадомцева,
Э. Г. Позняка, И. И. Юдиной
Автор-составитель Г. Ю, Ковтун
Волгоград
БЖ 74.262.21 гм
Автор-составитель Г. Ю. Ко вту н
Геометрия. 8 класс : технологические карты уроков по учебнику Л. С. Атанасяна,
Г36 В. Ф. Бутузова, С. Б. Кадомцева, Э. Г. Позняка, И. И. Юдиной / авт.-сост. Г. Ю. Ковтун. — Волгоград : Учитель, 2015. — 208 с.
ISBN 978-5-7057-4026-0
В пособии представлены технологические карты уроков по геометрии для 8 класса, разработанные в соответствии с ФГОС ООО и ориентированные на работу с учебником Л. С. Атанасяна, В. Ф. Бутузова, С. Б. Кадомцева, Э. Г. Позняка, И. И. Юдиной (М.: Просвещение, 2014).
Технологические карты уроков отражают современные виды и формы деятельности, способствующие развитию познавательной активности и коммуникативной компетенции, побуждающие учащихся осуществлять регулятивно-оценочные функции, формулировать учебнопрактические задачи и находить пути их решения.
Предназначено учителям математики, руководителям методических объединений.
ББК 74.262.21
Пособия издательства «Учитель» Допущены к использованию в образовательном процессе Приказом Министерства образования и науки РФ № 16 от 16.01.2012 г.
rsBN 978-54057-4026-0 © Ковтун Г. Ю., автор-составитель, 2014
© Издательство «Учитель», 2014
© Оформление. Издательство «Учитель», 2014 Издание 2015 г.
Геометрия является одним из опорных предметов основной школы: она обеспечивает изучение дисциплин естественно-научного и гуманитарного циклов; практические умения и навыки геометрического характера необходимы для трудовой деятельности и профессиональной подготовки школьников,
Геометрическая подготовка необходима для понимания принципов устройства и использования современной техники, восприятия научных и технических понятий и идей. Развитие у школьников правильных представлений о сущности и происхождении геометрических абстракций, соотношении реального и идеального, характере отражения математической наукой явлений и процессов реального мира, месте геометрии в системе наук и роли математического моделирования в научном познании и в практике способствует формированию научного мировоззрения учащихся. развитию качеств мышления, необходимых для адаптации в современном информационном обществе.
Требуя от учащихся умственных и волевых усилий, концентрации внимания, активного воображения, геометрия развивает нравственные черты личности (настойчивость, целеустремленность, творческую активность, самостоятельность, ответственность, трудолюбие, дисциплинированность и критичность мышления) и умение аргументированно отстаивать свои взгляды и убеждения, способность принимать самостоятельные решения.
Геометрия расширяет кругозор учащихся, знакомя их с
дедукцией и индукцией, обобщением и конкретизацией, анализом и синтезом,
классификацией и систематизацией, абстрагированием, аналогией. Активное
использование задач на всех этапах учебного процесса развивает творческие
способности детей. Геометрия занимает ведущее место в формировании
научнотеоретического мышления школьников, вносит значительный вклад в
эстетическое воспитание учащихся ![]()
В пособии представлены технологические карты уроков по геометрии для 8 класса, разработанные в соответствии с ФГОС ООО.
Цель данного пособия — практическая помощь учителю, особенно молодому, в выборе путей построения урока и форм организации учебной деятельности учащихся.
Планирование дается из расчета 2 часа в неделю (70 часов) в соответствии с распределением часов, предлагаемым Программой общеобразовательных учреждений. Структура пособия соответствует структуре базового учебника «Геометрия. 7—9 классы» Л. С. Атанасяна, В. Ф. Бутузова, С. Б. Кадомцева, Э. Г. Позняка, И. И. Юдиной (М.: Просвещение, 2014).
В пособии содержатся основные теоретические сведения, разнообразный дидактический материал, а также контрольные работы.
При отборе учебного материала автор-составитель преследовал цель совершенствовать практические навыки и умения учащихся, развивать их познавательную активность и коммуникативную компетентность, побуждать школьников осуществлять регулятивно-оценочную деятельность, формулировать учебно-практические задачи и находить пути их решения.
Надеемся, что предложенные поурочные планы окажут существенную помощь в подготовке и проведении уроков тем, кто будет работать по учебному пособию.
![]()
Геометрия. Сборник рабочих программ. 7—9 классы: пособие для учителей общеобразоват. учреждений / сост. Т. А. Бурмистрова. М.: Просвещение, 2011. С. 3—4.
ГЛАВА V. ЧЕТЫРЕХУГОЛЬНИКИ
Урок 1. Тема: МНОГОУГОЛЬНИКИ
|
Цель деятельности учителя |
Создать условия для формирования представлений о многоугольниках, о выпуклом многоугольнике, умений объяснять, какая фигура называется многоугольником, и называть его элементы; для рассмотрения четырехугольника как частного вида многогольника; для повто ения в ходе ешения задач п изнаков авенстват е гольников |
|
|
Те мины и понятия |
Вып клый, невып клый много гольник |
|
|
Плани емые ез льтаты |
||
|
П едметные мения |
Униве сальные чебные действия |
|
|
Умеют объяснять, что такое ломаная, многоугольник, его вершины, смежные стороны, диагонали; изображают и распознают многоугольники на чертежах; показывают элементы многоугольников, внутреннюю и внешнюю области многоу гольников |
Познавательные: умеют ясно, точно, грамотно излагать свои мысли в устной и письменной речи; воспринимают устную речь, проводят информационно-смысловой анализ текста и лекции, осмысливают ошибки и устраняют их. Регулятивные: понимают смысл поставленной задачи. Коммуникативные: выстраивают аргументацию, участвуют в диалоге, приводят примеры и контрпримеры. Личностные: выражают интерес к изучению предметного курса, проявляют готовность и способность к само азвитию, имеют мотивацию к об чению и познанию |
|
|
О ганизация п ост анства |
||
|
Фо мы аботы |
Ф онтальная (Ф ; индивид альная И |
|
|
Образовательные ресурсы |
• Геометрия. 7—9 классы: учеб. для общеобразоват. учреждений / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина. М.: Просвещение, 2014. • Задания для онтальной и индивид альной аботы |
|
|
этап. Ак ализация опо ных знаний |
||
|
ель деятельности |
Совместная деятельность |
|
|
Повторить основные элементы треугольника |
(Ф) Напомнить учащимся определение треугольника. Вспомнить элементы треугольника (сторона, вершина, угол) |
|
|
II этап. Мотивация к деятельности |
||
|
ель деятельности |
Постановка чебной задачи |
|
|
Ввести понятие много гольника |
(И/Ф) Рассмотреть рис. 1 50, 151 и 152 из учебника на с. 97—98. Что общего у этих геометрических фигур? |
|
|
III этап. Учебно-познавательная деятельность |
||
|
Из чение нового мате иала |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Ознакомить с выпуклыми и невыпуклыми много голышками |
(ИО) 1. Рассмотреть элементы многоугольника (вершины, стороны, диагонали, углы). (Ф) 2. Отметить, что каждый многоугольник разделяет плоскость на две области — внутреннюю и внешнюю. Ф З. Дать понятие вып клого много гольника |
|
ПроДол.тсение табл.
|
Закрепление изученного материала |
||||
|
Цель деятельности |
Обучающие и развивающие задания и упражнения |
Диагностические задания |
||
|
Закрепить полученные знания |
Рис.
Рис. |
Рис. 4 Рис. 5
Рис. 6 |
(Ф) 1 . Ответить на вопросы (устно): Какие фигуры, изображенные на доске, являются многоугольниками? Какие многоугольники являются выпуклыми? (И) 2. Задание для каждого ряда: Начертить выпуклый семиугольник, восьмиугольник, девятиугольник и провести все диагонали из какой-нибудь его вершины. (Ф) Сколько получилось треугольников? |
|
|
IV этап. Повто ение |
||||
|
Цель деятельности |
Обучающие и развивающие задания и упражнения |
Диагностические задания |
||
|
|
2 |
3 |
||
|
Повторить изученный материал |
Рис. 7 |
м
Рис. 8 Рис. 9 |
(И/Ф) Найти пары равных треугольников и доказать их равенство. Решение: Рис. 7. Назовем точку пересечения отрезков АС и BD точкой О. Тогда МОВ = ДСО (по первому признаку). Рис. 8. Так как ZN= ZP, ZMkN= ZPkE, как
вертикальные, Nk= КР по условию, значит, |
|
Окончание
|
|
2 |
з |
|
|
|
Рис. м Рис. в Рис. Рис. 15
Рис. 16 Рис. Рис. 18 |
Рис. 9. АС - общая, АВ = АД ZBAC = ZCAD, значит, ДАВС = = ДОС (по первому признаку). Рис. 10. О- общая, Ж) = ВС, ZADB = ZCBD, значит, МТ) = АСТ (по Ч)вому признаку). Рис. 1 1. DF- общая, ZMFD = ZEFD, ZMDF= ZEDF, тогда AMDF = AEDF (по второму признаку). Рис. П. АР - общая, ZNAP = ZNPA, ZM4P = ZMPA, тогда АМАР = ЛУАР (по второму признаку). Рис. В. ЛК- общая, кр, мО = КМ, значит, ЛПК = = ДРКЛГ (по третьему признаку). Рис. 14. Л- общая, ИТ = ZCBD, ИВЕ) = СЛ, значит, ДАЛ = ДСВГ) (по второму признаку). Рис. 15. Так Рис. 16. АС = ВС, ZC — общий, ZB = И, значит, ДСВЕ = ACAD (по второму признаку). Рис. 17. КН = НЕ, Fk= РЕ, углы, равные смежным, тоже равны, значит, ZFkH = ZPEH и тогда ДЕКН = ДРЕН (по первому признаку). Рис. 18. DE = ЕС, углы, равные смежным, тоже равны, тогда ZADE = ОСЕ, ZAED = ZBEC (как вертикальные), следовательно, MDE = АВСЕ (по второму признаку) |
|
|
V этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
— Какая фигура называется многоугольником? — Что такое вершина, сторона, диагонали и периметр многоугольника? — Какой многоугольник называется выпуклым? — Какой этап урока оказался наиболее трудным для вас и почему? |
(И) Домашнее задание: п. 40 прочитать; № 364, 365 |
||
У к 2. Тема: ВЫПУКЛЫЙ МНОГОУГОЛЬНИК
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Продолжение
|
|
2 |
|||||||||||||||||||||
|
|
Рис. Рис. 2 Рис. З Рис. 4 В ы вод:
Значит, сумма внутренних углов п-угольника равна 1 800 • (п — 2), где п — число сторон многоугольника. Сумма внешних углов п-угольника не зависит от количества сторон и всегда равна 360 0 . Объясните: почему? |
|||||||||||||||||||||
|
Закрепление изученного материала |
||||||||||||||||||||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
||||||||||||||||||||
|
Закрепить полученные знания |
(Ф) 1. Найдите сумму углов выпуклого: а) восьмиугольника; б) двенадцатиугольника. (Ф) 2. Сколько сторон имеет выпуклый многоугольник,если его сумма углов равна 2340 0 ? Решить № 364 (в), 365 |
1. а) п = 8; (8-2) • = 10800 . 6) п = 12; (12 -2) • = 1800 0 . 2. (п- 2) • 180 = 2340 11-2 = 13 п = 15 От в е т:
многоугольник имеет 15 сторон. ль 364. -
= 600 ; (п -2) • 0 = 60 0 п; п = З - 120 0 ; (п -2) • 180 120 0 п; п = 6 108 0 ; (п- 2) • 1800 = |
||||||||||||||||||||
|
III этап. Повторение |
||||||||||||||||||||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
||||||||||||||||||||
|
|
2 |
|
||||||||||||||||||||
|
Повторить изученный материал |
Параллельны ли прямые а, Ь и с? |
1 . Параллельны. |
||||||||||||||||||||
|
Цель деятельности учителя |
Создать условия для введения определения параллелограмма и его свойств |
|
Термины и понятия |
Параллелограмм, противолежащие стороны, противолежащие углы |
|
|
|
![]() Окончание пшол
Окончание пшол
|
|
2 |
|
|
|
|
Рис. 5 (Ф) 2. Параллельны ли прямые а и Ь?
Рис. 6 (Ф) 3. Параллельны ли прямые т и п, п и К, т и К?
Рис. 7 |
2. да. З. да |
|
|
IV этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
— Что нового узнали на уроке? — Какой этап урока оказался для вас самым сложным? — Оцените свою работу на уроке |
(И) Домашнее задание: вопросы 3—5, с. 1 13; № 368, 369 |
||
У р о к З. Тема: ПАРАЛЛЕЛОГРАММ. СВОЙСТВА ПАРАЛЛЕЛОГРАММА
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Умеют объяснять, какой многоугольник называется параллелограммом, точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии |
Познавательные: проводят информационно-смысловой анализ текста и лекции; осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, умением устанавливать причинно-следственные связи; понимают и используют наглядность для иллюстрации примеров, интерпретации математических фактов, аргументации собственного суждения. Регулятивные: принимают и сохраняют цели и задачи учебной деятельности; осуществляют планирование и контроль. Коммуникативные: договариваются и приходят к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные ресурсы |
• Учебник. • Задания для самостоятельной работы |
|
|
I этап. Проверка домашнего задания |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Выявить трудности у учащихся при выполнении домашней работы |
Обсудить выполнение домашней работы (решение задач), ответить на вопросы учащихся |
|
|
II этап. Самостоятельная работа |
||
|
Цель деятельности |
Задания для самостоятельной работы |
|
|
|
2 |
|
|
Выявить у учащихся умение находить сумму углов многоугольников |
(И) Вариант 1 1. Найдите сумму углов выпуклого тринадцатиугольника. (1980 0.) 2. Каждый угол выпуклого многоугольника равен 135 0 . Найдите число сторон этого многоугольника. (8.) Вариант П 1. Найдите сумму углов выпуклого двенадцатиугольника. (1800 0.) 2. Сумма углов выпуклого многоугольника с равными углами равна 1260 0 . Найдите число сторон этого многоугольника. (9.) |
|
|
|
2 |
|
|
|
Ва р и а нт III (для более подготовленных учащихся) Каждый угол данного выпуклого многоугольника равен 1500 . Найдите сумму углов выпуклого многоугольника, число сторон которого в два раза меньше, чем число сторон данного многоугольника. ((п —2) • 180 0 150n; п 12 — число сторон исходного многоугольника; 6 сторон у второго многоугольника. Сумма его углов 720 0.) |
|
|
|
этап. Учебно-познавательная деятельность |
|
|
|
Изучение нового материала |
|
|
Цель деятельности |
Совместная деятельность |
|
|
Дать определение параллелограмма и доказать его свойства |
(Ф) 2. Рассмотреть свойства параллелограмма: • В параллелограмме противоположные стороны и противоположные углы равны. • Диагонали параллелограмма точкой пересечения делятся пополам. (Ф) З. Доказать любое свойство параллелограмма в классе, на дом предложить доказательство второго свойства |
|
|
|
Закрепление изученного материала |
|
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
Закрепить полученные знания |
1. Докажите, что сумма углов, прилежащих к одной стороне параллелограмма,•равна 180 0 . 2. Решите задачи № 376 (а) (устно); № 376 (б), 372 (а). |
ЛГ2 376 И = ZC = 84 0 ,0 = О = - 84 0 = 960 . .N2 376 (б). Можно решить системой уравнений: И- = 55 0 ; И + 180 0 ; И = 1 17,5 0 , О = 62,5 0 № 372 (а). Пусть одна сторона х см, тогда вторая (х + З) см. Так как периметр равен 48 см, то составим и решим уравнение: (х + х + 3) • 2 = 48; х = 10,5; таким образом, одна сторона равна 10,5 см, вторая — 13,5 см |
|
|
IV этап. Итоги урока |
|
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
|
2 |
|
|
Подвести итог изученному теоретическому материалу |
(Ф) Если в условии задачи дано, что ABCD — параллелограмм, то можно использовать его свойства: |
|
|
Цель деятельности чителя |
Создать условия для рассмотрения признаков параллелограмма и закрепления полученных знаний в процессе решения задач |
|
|
Те мины и понятия |
Параллелограмм, противолежащие стороны, противолежащие углы |
|
|
Планируемые результаты |
||
|
П едметные умения |
Универсальные учебные действия |
|
|
Умеют объяснять, какой многоугольник называется параллелограммом, точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии |
Познавательные: проводят информационно-смысловой анализ текста и лекции; осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, умением устанавливать причинно-следственные связи; понимают и используют наглядность для иллюстрации, интерпретации, аргументации. Регулятивные: принимают и сохраняют цели и задачи учебной деятельности. Коммуникативные: договариваются и приходят к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
|
|
Организация пространства |
||
|
Фо мы аботы |
Фронтальная (Ф); групповая (Г); индивидуальная (И) |
|
|
Образовательные есу сы |
• Учебник. • Задания для индивидуальной работы |
|
|
|
2 |
|
|
|
|
АВ СД ВС АО, АВ СД ВС = АО, U ZC, ZD•, И + О = ит. д.; АО = ОС, ВО- Од
Рис. 2 |
|
|
|
V этап. Рефлексия |
|||
|
Деятельность учителя |
Деятельность чащихся |
||
|
(ФМ) Составьте синквейн к уроку |
(И) Домашнее задание: вопросы 6—8, с. 13; № 372 (б), 376 (в, г), 374; доказать одно из свойств параллелограмма (то, которое в классе не доказывали) |
||
У р о к 4. Тема: ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА
|
этап. Актуализация опорных знаний |
||
|
Цель деятельности |
Деятельность учителя |
Деятел ьность учащихся |
|
|
2 |
3 |
|
Повторить основные элементы параллелограмма, его свойства и признаки |
(Ф/И) 1. Дает задание подготовить у доски свойства параллелограмма с доказательством (для учащихся со слабым уровнем подготовки). (Выслушать ИнДИвиДуально каждого отвечающего.) (ФМ) 2. Дает задание доказать самостоятельно следующие свойства параллелограмма (для учащихся с высоким уровнем подготовки): I ) Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник. 2) Биссектрисы соседних углов параллелограмма перпендикулярны, а биссектрисы противоположных углов параллельны или лежат на одной прямой. (После поДготовки выслушать Доказательства дополнительных свойств параллелограмма.) Наводящие вопросы: — Сформулируйте признак равнобедренного треугольника. — Какие углы в ЛВАЕ могут быть равными? Почему? |
1 ) Дано: ABCD — параллелограмм, АЕ — биссектриса ZBAD.
Доказательство: так как ABCD — параллелограмм, значит ВС АД тогда ZEAD ZBEA, как накрест лежащие при параллельных прямых ВС и AD и секущей АЕ. АЕ — биссектриса ZBAD, значит ZBAE =ZEAD, поэтому ZBAE = ZBEA. В МВЕ ZBAE = ZBEA, значит, ЛАВЕ — равнобедренный с основанием АЕ.
СВА, АЕ — биссектриса ZBAD. Доказать: ВЕ -L АЕ. Доказательство: АЕ — биссектриса, следовательно Zl = Z2. ВЕ— биссектриса гэ Z3 = д. В параллелограмме сумма углов, прилежащих к од- Рис. 2 ной стороне, равна 1 80 0 , поэтому ЛВС + ZBAD = — 180 0 , то есть Z1 + Z2 +Z3 + Z4 = 1 80 0 Так как д = П, Z3 = д, то 2 • ( д + Д) = 180 0 , Д + = 90 0 . В ЛАВЕ ИЕВ = 180 0 - (д + Z3) = 90 0 , то есть ВЕ МЕ. |
|
|
2 |
|
|
|
Наводящие вопросы: — Когда прямые АЕ и СК будут параллельными? — Равны ли ZBEA и Z3? Почему? — В каком случае АЕ и СК совпадут? |
26) Дано: ABCD — параллелограмм, АЕ, СК— биссектрисы ZA = С. Доказать: АЕ ll СК или АЕ и СК совпадают.
В параллелограмме противолежащие углы равны, следовательно, ZBAD = ZBCD, значит, А к D Рис. З Д = П = а = д. Так как П = ZBEA, Z2 = Z3, то ZBEA = Z3 прямые АЕ и СК параллельны по признаку параллельности прямых. Прямые АЕ и СК совпадут, если в параллелограмме смежные стороны равны |
|
П этап. Мотивация к деятельности |
||
|
Цель деятельности |
Постановка учебной задачи |
|
|
Создать условия для введения признаков параллелограмма |
(Ф) — Что означают слова «свойства» и «признак»? Приведите примеры. — Какую теорему называют обратной? — Всегда ли верно утверждение, обратное данному? Приведите примеры |
|
|
III этап. Учебно-познавательная деятельность |
||
|
Изучение нового материала |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Сформулировать признаки параллелограмма |
(Ф) — Сформулируйте утверждения, обратные свойствам параллелограмма. Всегда ли они верны? (Г/Ф) Далее учащихся можно распреДелить на группы (по рядам) для учебно-исслеДовательской работы. Обсудить Доказательства, сДелать запись на Доске и в тетраДи. . Если АВ = CD и АВ CD, то ABCD — параллелограмм.
Рис. 4 |
|
|
|
2 |
||||
|
|
2. Если АВ = CD и ВС = О, то ABCD параллелограмм.
З. Если АС п BD - О, АО - ОС и ВО - ОС, то ABCD — параллелограмм.
Рис. 6 |
||||
|
Закрепление изученного материала |
|||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
||
|
Закрепить полученные знания |
(Ф/И) 1. Решите задачу № 379 (на доске и в тетради). (И) 2. Решите задачу № 380 (самостоятельно) |
дано: ABCD - параллелограмм, вк АС, тиш Доказать: ВМЛ— параллелограмм. Доказательство: 1) ЛВКМ = z\DMA по гипотенузе и острому углу (ZBCk = ZDAC, как накрест лежащие углы при параллель- А ных прямых AD и ВС и секущей АС, ВС = АД как противолежащие стороны параллелограмма, АВКС и ОМА прямоугольные), значит MD = ВК. 2) ДВМК и ДЛМ— прямоугольные, ДВМК = катетам (MD = ВК, КМ— общий катет), значит, 3) В четырехугольнике BMDk противолежащие ны (MD = ВК и ВМ = Л), следовательно, грамм |
АС.
D Рис. 7 М)КМ по двум ВМ= Dk. стороны рав- ВЬЮК— параллело- |
с |
|
|
1V этап. Итоги урока. Рефлексия |
|||||
|
Деятельность учителя |
Деятельность учащихся |
||||
|
(Ф/И) Если в задаче необходимо доказать, что ABCD — параллелограмм, то применяют один из признаков: |
(И) Домашнее задание: выучить признаки параллелограмма; решить № 382, 383 |
||||
Окончание
|
|
2 |
|
1. Если АВ = CD и АВ СД то ABCD - параллелограмм. 2. Если АВ = CD и ВС = АД то ABCD — параллелограмм. З. Если АС П BD= О, АО = ОС и ВО = ОС, то ABCD — параллелограмм. — На каком этапе урока у вас возникли трудности? |
|
У р о к 5. Тема: РЕШЕНИЕ ЗАДАЧ ПО ТЕМЕ «ПАРАЛЛЕЛОГРАММ»
|
Цель деятельности учителя |
Создать условия для закрепления знаний о свойствах и признаках параллелограмма в процессе решения задач |
|
|
Термины и понятия |
Выпуклый, невыпуклый многоугольник |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Умеют точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии |
Познавательные: умеют ясно, точно, грамотно излагать свои мысли в устной и письменной речи; воспринимают устную речь; проводят информационно-смысловой анализ текста и лекции; осмысливают ошибки и устраняют их. Регулятивные: понимают смысл поставленной задачи. Коммуникативные: договариваются и приходят к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов. Личностные: выражают интерес к изучению предметного курса; проявляют готовность и способность к саморазвитию; имеют мотивацию к обучению и познанию |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); парная (П); индивидуальная (И) |
|
|
Образовательные ресурсы |
• Учебник. • Задания для работы по индивидуальным карточкам, для самостоятельной работы по вариантам, для парной работы |
|
|
I этап. Актуализация опорных знаний |
||
|
Цель деятельности |
Задания для самостоятельной работы |
|
|
Повторить основные свойства и признаки параллелограмма |
(И) Работа по индивидуальным карточкам (3—6 человек). 1-й уровень. 1 . Точки Е и К — середины сторон АВ и CD параллелограмма ABCD. Докажите, что АЕСК — параллелограмм. 2. Диагонали четырехугольника ABCD пересекаются в точке О, причем АС = 2 дм, АО = 10 см, BD = 1,5 дм, ВО = см Выясните, является ли ABCD параллелограммом. |
|
|
|
2 |
||
|
|
2-й уровень. 1. В параллелограмме ABCD на сторонах АВ и CD отмечены соответственно точки Ми дг так, что ZBMC = ZAND. Докажите, что AMCN — параллелограмм. 2. Точки А и В делят диагональ МК параллелограмма MNkP на три равные части. Является ли четырехугольник ANBP параллелограммом? Ответ обоснуйте. 3-й уровень. дано: ABCD - параллелограмм, СК, АР = CN (рис. 1). Доказать: MNkP — параллелограмм.
Рис. (И) Остальные учащиеся выполняют самостоятельную работу по вариантам. Вариант 1 1. В четырехугольнике ABCD АВ CD и АВ = CD, АС = 1 0 см, BD = 5 см, АВ = 6,5 см. Диагонали четырехугольника пересекаются в точке О. Найти периметр треугольника СОД 2. В параллелограмме ABCD из вершины В тупого угла АВС проведен перпендикуляр ВК к стороне AD (К е AD) и ВК = 0,5АВ. Найти углы параллелограмма. Вариант П 1. В четырехугольнике ABCD О — точка пересечения диагоналей и ВС АД АВ = CD, АС = 1 6 см, BD = 14 см, Риов= 25 см. Найти АВ. 2. В параллелограмме ABCD из вершины В тупого угла опущен перпендикуляр ВК на сторону AD и АК = ВК. Найти углы параллелограмма |
||
|
П этап. Решение задач по готовым чертежам |
|||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
|
1 |
2 |
|
|
|
Повторить основные свойства и признаки параллелограмма |
в . ABCD — параллелограмм. Найти: ZC, О. lOc 2. №INkP — параллелограмм. Найти: МГ), РК. м |
к
|
— 64 0 , ZD- 1160. 2. ЛО- 4 см, РК- 10 см. |
Продолжение
|
|
2 |
|
|
|||
|
|
З. Найти углы параллелограмма 4. ABCD — параллелограмм. Найти: РАЖУ). 2 5. ABCD — параллелограмм. Найти: АД 6. ABCD — параллелограмм. Найти: РИТ), ZAED. 7. NBFD — параллелограмм. AD = 4 5 см. Найти: ВС, CD. 8. ABCD — параллелограмм. РММ<Р = 20 см. Найти: MN, МР. |
ABCD.
см, 5 см м |
в з
|
с
в Рис. 5 с 8 Рис. б 5 Рис. 7
Рис. 8
|
З. = 115 0 , U = 4. РАВ('Г)— l6 см.
6. PABCD=
ЗО см, ZAED = 900 7. вс=4 см, CD=5 см. 8. лт=з см, см |
65 0 . |
Окончание
|
|
2 |
З |
|
|
|
Рис. 10 |
|
|
|
III этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
— Какие свойства и признаки параллелограмма повторили на уроке? — Оцените свою работу на уроке |
(И) Домашнее задание: разобрать по учебнику № 385 (Теорему Фалеса), решить задачу:
Доказать: ABNM— параллелограмм. |
||
Урок 6. Тема: ТРАПЕЦИЯ
|
Цель деятельности учителя |
Создать условия для введения понятий «трапеция», «равнобокая трапеция», «прямоугольная трапеция»; для рассмотрения решения задач, в которых раскрываются свойства трапеции |
|
|
Термины и понятия |
Трапеция, основания трапеции, боковые стороны |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Умеют объяснять, какой многоугольник называется трапецией, точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии |
Познавательные: проводят информационно-смысловой анализ текста и лекции; осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, умением устанавливать причинно-следственные связи. Регулятивные: принимают и сохраняют учебную задачу. Коммуникативные: умеют применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач, работать в группе. Личностные: умеют контролировать процесс и результат учебной математической деятельности |
|
Продолжение
|
|
Организация пространства |
|
|
Формы работы |
Фронтальная (Ф); индивидуальная (И); групповая (Г) |
|
|
Образовательные ес сы |
• Учебник. • Задания для индивидуальной работы |
|
|
|
этап. П оверка домашнего задания |
|
|
Цель деятельности |
Совместная деятельность |
|
|
Выявить трудности, возникшие при вы- ПОЛНеНИИ домашнего задания |
(Ф) 1. Сформулируйте и докажите теорему Фалеса. 2. Сформулируйте свойства параллелограмма. 3. Сформулируйте признаки параллелограмма |
|
|
|
П этап. Учебно-познавательная деятельность |
|
|
|
Изучение нового мате иала |
|
|
Цель деятельности |
Совместная деятельность |
|
|
Ввести понятие траПеЦИИ, ее оснований и боковых сторон |
ABCD— трапеция, если ВС И АД АВ и CD — боковые стороны, ВС и AD —основания. 2. Ввести понятия равнобедренной и прямоугольной трапеции.
Рис. 2 Рис. З |
|
|
|
Учебно-исследовательская деятельность |
|
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
|
2 |
|
|
Сформулировать свойства равнобедренной трапеции |
(Г) Класс разбивается на несколько групп для обсуждения свойств и признаков равнобедренной трапеции. З ад а н и е : исследовать углы равнобедренной трапеции, диаГОНИИ трапеции. |
|
|
|
2 |
3 |
|
|
Результаты исследований выслушать и обсудить, на доске и в тетрадях выполнить запись: Свойства равнобедренной трапеции: . В равнобедренной трапеции углы при
каждом основании равны. Рис. 4 2. В равнобедренной трапеции диагонали равны.
Рис. 5 З ад а н и е : сформулируйте утверждения, обратные свойствам равнобедренной трапеции, и докажите их справедливость. Результаты исследований выслушать и обсудить, на доске и в тетрадях выполнить запись: I . Если углы при основании трапеции равны, то она равнобедренная.
2. Если диагонали трапеции равны, то она равнобедренная.
Рис. 7 |
оказательство: Проведем СЕ МВ. АВСЕ - параллелограмм (АВ СЕ, ВС П AD). CD = АВ = СЕ, ДОЕ- равнобедренный, Д = п. АВ СЕ, тогда Z2 = д. Д = П = д. ЛВС = - д = 1800 - д = ZBCD Доказательство: ЛАВС = ОСВ (АВ = DC, ВС - общая сторона, ЛВС = = ОСВ), тогда АС = ВД Доказательство: Проведем СЕ АВ. АВСЕ — параллелограмм, тогда АВ = СЕ, ZA = ZCED. ДСО — равнобедренный (ZD = ZCED), тогда СЕ = CD. АВ = СЕ = CD, тогда ABCD — равнобедренная трапеция. Доказательство: Проведем ск ВД ВСО - параллелограмм (СК ВД ВС АК). МСК— равнобедренный (АС = BD = СК), Zl = П. СК П ВД Z2 = Z3, тогда Zl = Z3. MBD = ОСА (АС = ВД AD — общая сторона, Zl = Z3), тогда АВ = CD, то есть ABCD — равнобедренная трапеция |
|
Цель деятельности учителя |
Создать условия для закрепления понятий «трапеция», «равнобокая трапеция», «прямоугольная трапеция»; для рассмотрения решения задач, в которых раскрываются свойства трапеции |
|
|
Термины и понятия |
Трапеция, основания трапеции, боковые стороны, параллелограмм, свойства, признаки |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Умеют объяснять, какой многоугольник называется трапецией, точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии |
Познавательные: проводят информационно-смысловой анализ текста и лекции; осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, умением устанавливать причинно-следственные связи. Регулятивные: принимают и сохраняют учебную задачу. |
|
Окончание
|
III этап. Решение задач |
|||
|
Цель деятельности |
Обучающие и развивающие задания и упражнения |
Диагностические задания |
|
|
Ввести понятие средней линии трапеции |
(Ф) ЛФ 386 (по теореме Фалеса). После решения этой задачи можно дать определение средней линии трапеции.
Рис. 8 М— середина АВ, N— середина CD, №IN— средняя линия траПеЦИИ |
№ 386. Доказательство: Пусть М— середина АВ. Проведем MN AD ВС. Точка N— середина CD (по теореме Фалеса). Докажем, что MN— единственная. Через точки Ми можно провести только одну прямую (по аксиоме), то есть отрезок, соединяющий середины 60ковых сторон, единственен и AD ll ВС |
|
|
IV этап. Итоги урока |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
(Ф) 1 . Какой четырехугольник называется трапецией? 2. Назовите элементы трапеции и ее виды. 3. В решении задач на трапецию можно использовать свойства углов при параллельных прямых и секу щей |
|
||
|
V этап. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
(ФМ) I . Оцените свою работу на уроке. 2. Какой этап урока вызвал у вас наибольшее затруднение и почему? 3. Составьте синквейн к уроку |
(И) Домашнее задание: выучить теоретическую часть; решить № 384, 387 |
||
Уро к 7. Тема: РЕШЕНИЕ ЗАДАЧ ПО ТЕМЕ «ПАРАЛЛЕЛОГРАММ. ТРАПЕЦИЯ»
|
|
|
Коммуникативные: умеют применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач, работать в группе. Личностные: умеют контролировать процесс и результат учебной математической деятельности |
|
|
|
О ганизация п ост анства |
||
|
Фо мы аботы |
Ф онтальная Ф ; индивид альная И |
||
|
Образовательные ес сы |
• Учебник. • Задания для онтальной, индивид алычой, па ной аботы |
||
|
|
I этап. П ове ка домашнего задания |
||
|
ель деятельности |
Совместная деятельность |
||
|
Выявить трудности, возникшие при выполнении заданий домашней работы; проверить уровень усвоения теоретического материала |
(Ф) 1 . Дайте определение трапеции. 2. Какие виды трапеций существуют? З. Перечислите свойства равнобедренной трапеции |
||
|
|
П этап. Решение задач |
||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
|
|
2 |
|
|
|
Создать условия для применения теоретических знаний при решении задач |
дано: ABCD -трапеция, МК— средняя линия. В, МК = 25. Найти: АД Решение задач по готовому чертежу (устно): I . MN— средняя линия трапеции ABCD, PR — средняя линия трапеции АЛПИ).
D Рис. 2 |
Так как МК = (ВС +0) : 2 = 25, то ВС +AD = 50, 50- В = 37 см. Ответ: 37 см. l.MN= 8 |
|
|
|
2 |
|
|
|
2. Чем являются отрезки МК и kN, если MN— средняя линия трапеции АВСТ
Рис. З |
2. МК-средняя линия ДАВС, kN— средняя линия MCD |
|
этап. Работа в парах |
||
|
Цель деятельности |
Задания для самостоятельной аботы |
|
|
|
2 |
|
|
Создавать условия для формирования навыков решения задач |
На каждом столе расположен листок с напечатанными задачами. Задача 1. Большее основание трапеции равно 8 см, а меньшее на З см меньше средней линии. Найти: ВС, МК. Дано.
ВС — ? на 3 см меньше МК. Найти: ВС, МК. Решение. Пусть ВС = х см. тогда МК = (х + 3) см МК = (О + ВС) : Ответ: ВС = 2 см, МК = 5 см. Задача 2.
Дано: ABCD — равнобокая трапеция. Р— 54 дм. Найти: ВС. Решение: Рис. 5 Zl = Z2 так как АС — биссектриса ZA, — Z3, как внутренние накрест лежащие углы. |
|
|
|
2 |
|||
|
|
Zl и = Zl Z3 ЛАВС-равнобедренный. пусть АВ = ВС = CD = х. Уравнение: 3х+ 18 = 54 3x= 54- 18 3х= 36 х- 12 Ответ: ВС дм. Задача 3.
ABCD — равнобокая трапеция, ВС — 16 см. АК — биссектриса ZA вк = кс MN— средняя линия Х-А = 60 0 Найти: МЛГ. Рис. 6 Решение:
Так как К— середина ВС, то ВК = КС = ВС : 2 = 16 см : 2 = 8 см. Так как АК— биссектриса Х-А, то Z1 = Z2; Z2 = Z3 как внутренние накрест лежащие углы. И = ZD, АВ = CD, МВЕ = M)CF (по гипотенузе и острому углу). Значит, АЕ DF, ZABE = 30 0 , МВЕ — прямоугольный. DF=4 см, ЕЕ = ВС = см, 16 +4+4=24 см. (ВС +AD) : 2 = + 24) : 2 = 20 см. Ответ: 20 см |
см, пополам. |
Найдите |
|
|
|
IV этап. Самостоятельная работа |
|
|
|
|
Цель деятельности |
|
Задания для самостоятельной работы |
|
|
|
Повторить свойства и признаки параллелограмма |
(И) 1 . В параллелограмме один из углов в два раза меньше другого. Найти углы параллелограмма. 2. На рисунке ABCD — параллелограмм. Zl= Z2. Докажите, что АТСК— параллелограмм. |
Рис. 7 |
к 2 |
|
Окончание
|
IV этап. Итоги урока. Рефлексия |
|
|
Деятельность учителя |
Деятельность учащихся |
|
— Составьте синквейн к уроку. — Оцените свою работу на уроке |
(И) Домашнее задание: № 379, 380 |
Урок 8. Тема: ТРАПЕЦИЯ. ЗАДАЧИ НА ПОСТРОЕНИЕ
|
Цель деятельности учителя |
Создать условия для решения задач, в которых применяются свойства и признаки трапеции |
||
|
Термины и понятия |
Трапеция, основания трапеции, боковые стороны, равнобедренная трапеция, прямоугольная трапеция, теорема Фалеса |
||
|
Планируемые результаты |
|||
|
Предметные умения |
Универсальные учебные действия |
||
|
Умеют применять полученные знания при решении задач и доказательстве |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, умением устанавливать причинно-следственные связи; понимают и используют средства наглядности. Регулятивные: принимают и сохраняют учебную задачу. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют познавательный интерес к изучению предмета |
||
|
Организация пространства |
|||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
||
|
Образовательные ресурсы |
• Учебник. • Задания для самостоятельной работы |
||
|
этап. Проверка домашнего задания |
|||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
|
Выявить трудности, возникшие при выполнении домашнего задания |
(Ф) 1. Сформулируйте теорему Фалеса. 2. Сформулируйте свойства равнобедренной трапеции |
1. Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки. 2. В равнобедренной трапеции углы при основаниях равны, диагонали равны |
|
|
П этап. Самостоятельная абота |
|
|
Цель деятельности |
Задания для самостоятельной аботы |
|
Проверить степень усвоения теоретического материала и умение его применять при решении задач |
Вариант 1 Найдите боковые стороны равнобедренной трапеции, основания которой равны 14 см и 8 см, а один из углов равен 120 0
Вариант П Найдите меньшее основание равнобедренной трапеции, если ее большее основание равно 16 см, боковая сторона —10 см, а один из углов равен 60 0 . 16 см,
Вариант III Диагональ АС равнобедренной трапеции ABCD делит пополам угол ВАД Найти периметр трапеции, если основание AD равно 12 см, а ZADC равен 60 0 . CD = 0,50, значит, CD = 6 см. ЛАВС — равнобедренный, ВС = 6 СМ, РАЖ , D= 6+6 + 6+ 12=30 см.
Далее проводится взаимоп ове ка |
|
III этап. Решение задач на пост оение |
|
|
Цель деятельности |
Совместная деятельность |
|
|
2 |
|
Повторить основные этапы решения задач на построение |
(Ф) . Напомнить основные этапы решения задач на построение: 1) Анализ задачи. 2) Выполнение пост оения по намеченном плану. |
Продолжение
|
|
2 |
|
|
3) Доказательство того, что построенная фигура удовлетворяет условиям задачи. 4) Исследование задачи. (ФИ) 2. Решить ЛЬ 393 (в), 395, 397 (а).
Построить ABCD — параллелограмм. И = zhk, АВ = РО РО — расстояние между АВ и CD. Устно провести анализ, доказательство и исследование, в тетрадях — только построение: 1) построить ZA, равный данному Zhk; 2) отложить на его стороне отрезок РО = АВ и отметить точку В; 3) через точку В провести прямую, перпендикулярную прямой АВ, и отложить отрезок ВК =рюх, 4) через точку В провести прямую, параллельную другой стороне угла; 5) через точку К провести прямую, параллельную стороне АВ; 6) ABCD — параллелограмм по определению. ЛЬ 397 (а). дано: И = а, о = а, АВ=Ь Построить: равнобедренную трапецию ABCD. Построение: 1. На прямой с отложить отрезок АЕ) = а. 2. Построить ZA = а, ZD = а. 3. На лучах АВ и DC отложить отрезки, равные Ь (АВ = DC = Ь). 4. Соединить В и С отрезком. ABCD — искомая трапеция. Задача может не иметь решения, если точки В и С совместятся или точки В и С расположены за точкой пересечения лучей АВ и DC. а) |
Окончание
|
IV этап. Итоги урока. Рефлексия |
|
|
Деятельность учителя |
Деятельность учащихся |
|
— Оцените свою работу на уроке. — Какой этап урока вызвал у вас наибольшее затруднение и почему? |
(И) Домашнее задание: решить задачи № 394, 398, 393 (б) |
Урок 9. Тема: ПРЯМОУГОЛЬНИК
|
Цель деятельности учителя |
Создать условия для введения определения прямоугольника, изучения свойств прямоугольника |
||
|
Термины и понятия |
Прямоугольник, диагонали прямоугольника |
||
|
Планируемые результаты |
|||
|
Предметные умения |
Универсальные учебные действия |
||
|
Умеют работать с геометрическим текстом, точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики |
Познавательные: умеют выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки; понимают и используют наглядность в решении учебных задач. Регулятивные: проявляют познавательный интерес к изучению предмета. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: умеют контролировать процесс и результат учебной математической деятельности |
||
|
Организация пространства |
|||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И); групповая (Г) |
||
|
Образовательные ресурсы |
• Учебник. • Задания для индивидуальной работы |
||
|
этап. Проверка домашнего задания |
|||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
|
|
2 |
З |
|
|
Выявить трудности, возникшие при выполнении домашнего задания |
I . Сформулируйте теорему Фалеса. 2. Сформулируйте свойства равнобедренной трапеции. |
1. Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки. 2. В равнобедренной трапеции углы при основаниях равны, диагонали равны. |
|
Продолжение
|
|
2 |
|
||||||||||||
|
|
3. Решите |
3. ЛАВС — равнобедренный. ZBAC = ZBCA = хо, как внутренние накрест лежащие при ВС AD и секущей АС, ZBAD = ZCDA = 2х 0. Из прямоугольного MCD: ZCAD + ZCDA = 90 0 х = 30 0 . В трапеции ABCD ZBAC = ZCAD = 60 0 , ZBCD = 1200 |
||||||||||||
|
П этап. Из чение нового мате иала |
||||||||||||||
|
ель деятельности |
Совместная деятельность |
|||||||||||||
|
|
2 |
|||||||||||||
|
Ввести понятие прямоугольника, доказать свойства и признаки прямоугольника |
1. Ввести понятие прямоугольника. Учащиеся знакомы с прямоугольником еще с начальной школы, поэтому ввести понятие прямоугольника можно в процессе беседы по вопросам: — Какой четырехугольник называется прямоугольником? (Ученики могут дать различные ответы, например: «Это четырехугольник, у которого все углы прямые»; «Это четырехугольник, у которого противолежащие стороны равны») — Можно ли утверждать, что прямоугольник — это параллелограмм, и почему? — Чем отличается произвольный параллелограмм от прямоугольника? — Закончите предложение: «Прямоугольник — это параллелограмм, у которого...» — Сформулируйте свойства прямоугольника. (ИТ) 2. Рассмотреть особое свойство диагоналей прямоугольника. — Исследуйте стороны, углы и диагонали прямоугольника и заполните таблицу.
(И/Ф) З. Рассмотреть признак прямоугольника. — Как определить, является ли данный параллелограмм прямоугольником? Ответ обоснуйте. (Дать учащимся 3—5 минут на обдумывание и обсудить варианты ответов.) (Ф) — Выберите верные утверждения (устно): а) Если в четырехугольнике диагонали равны и делятся точкой пересечения пополам, то этот четырехугольник— прямоугольник. б) Если в четырехугольнике противоположные стороны параллельны, а все его углы прямые, то этот четырехугольник — прямо гольник. |
|||||||||||||
Продолжение
|
|
2 |
|||||||||||
|
|
в) Если в четырехугольнике диагонали равны, то этот четырехугольник — прямоугольник. г) Если в параллелограмме два угла прямых, то этот параллелограмм — прямоугольник. д) Если в четырехугольнике два прямых угла и две стороны равны, то этот четырехугольник — прямоугольник. е Если в четы ех голышке диагонали авны, а один гол п ямой,то этот четы ех гольник—п ямо гольник |
|||||||||||
|
III этап. Решение задач |
||||||||||||
|
Цель деятельности |
еятельность чителя |
|
еятельность чащихся |
|
|
|||||||
|
Совершенствовать навыки решения задач, опираясь на полученные знания |
(И/Ф) . Решите задачу: В прямоугольнике ABCD биссектриса угла D пересекает сторону АВ в точке М. Докажите, что ДОМ— равнобедренный. Найдите периметр прямоугольника, если сторона АВ оказалась разбита на отрезки длиной З см и 5 см. Сколько решений имеет задача? 2. Решите № 403. Дано: ABCD — прямоугольник, АС П BD = О, ZCAD = 30 0 ,
|
1. Решение: з AD=3 Р ЛЬ 403.
Решение: MCD АС — 6 2 диагонали АС АО2 АОВ От вет : |
Рис. З — см, равны и Т) = 2
|
5 Рис. в с прямоугольный, тогда АВ = точкой ВО = 6 см. |
в
в нем CD = 6 см. В
пересечения делятся
|
ZCAD = 30 0 , прямоугольнике пополам, |
з в с Рис. 2 значит, то есть |
|||||
|
IV этап. Итоги ока. Ре лексия |
||||||||||||
|
Деятельность учителя |
Деятельность чащихся |
|||||||||||
|
|
2 |
|||||||||||
|
(Ф) |
BCD— прямоугольник |
|
щ сд вс о, СД ВС АД о = ос, во = OD |
|
(И) Домашнее задание: п. 46 прочитать, решить № 401, 404 |
|||||||
|
|
||||||||||||
Окончание таоп.
|
|
2 |
|||||||||||||||||||
|
|
|
|||||||||||||||||||
Урок Ш. Тема: РОМБ. КВАДРАТ
|
Цель деятельности учителя |
Создать условия для введения понятий ромба и квадрата как частных видов параллелограмма, для рассмотрения свойств и п изнаков ромба и квадрата; показать их применение в процессе решения задач |
|
|
Термины и понятия |
Ромб, квадрат, диагонали, углы |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
У меют работать с геометрическим текстом, точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики |
Познавательные: умеют выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки; понимают и используют наглядность в процессе решения задач. Регулятивные: проявляют познавательный интерес к изучению предмета. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: умеют контролировать процесс и результат учебной математической деятельности |
|
|
Организация п остранства |
||
|
Фо мы аботы |
Ф онтальная (Ф); индивидуальная (И); групповая (Г) |
|
|
Образовательные ес сы |
• Учебник. • Задания для фронтальной, групповой работы |
|
|
1 этап. П оверка домашнего задания |
||
|
Цель деятельности |
Совместная деятельность |
|
|
|
2 |
|
|
Выявить трудности, возникшие при выполнении домашнего задания |
(Ф) 1. Дайте определение прямоугольника. 2. Перечислите свойства прямоугольника. Докажите одно из них. З. Перечислите признаки прямоугольника. 4. Решите задачу: Через середину диагонали КМ прямоугольника kLMN перпендикулярно этой диагонали проведена прямая, пересекающая стооны kL и ЛТ в точках А и В соответственно. Известно, что АВ = ВМ = 6. Найдите ббльшую сторону прямоугольника. |
|
Продолжение
|
|
2 |
|
|
|
|
а) Прямоугольные ЛМОВ и МОА равны по катету и прилежащему так как О — середина диагонали КМ; ZBMO = ИКС), как накрест мых kL и МЛ[и секущей КМ), тогда АО = ОВ = 3 см (АВ = 6 см), АК б) ДАМО = ДВМО по двум катетам (АО = ВО, МО — общая сторона, АМ= МВ = 6 см и ММВ — равносторонний. в) ZAMO = ZBMO = 30 0 , так как ММВ — равносторонний, МО — г) ZkLM= 90 0 , ИМО = 30 0 , оМО = 300 , тогда ИШ = 30 0 . д) MLM— прямоугольный, в нем ZAML = 300 , АМ= 6 см, тогда М е) АК = 6 см, AL = 3 см, тогда kL = 9 см. 5. Решите задачи по готовым чертежам: 1) ABCD — прямоугольник. Найти: ZABF. в Рис. 2 3) ABCD— прямоугольник. Доказать:ЯМ = М)
Рис. 4 5) ABCD -прямоугольник. Найти: АС, АВ.
Рис. 6 |
ДОМ = ZMOB = 90 0), тогда медиана, высота и биссектриса ММВ. = 3 см. Рис. 2) АСЕК-прямоугольник, ВС = 5 см. Найти: PBDFM.
4) ABCD - прямоугольник. Найти: ИОВ, ПОС.
Рис. 5 6) ABCD — прямоугольник. Найти: АД
Рис. 7 |
м |
Продолжение табл.
|
II этап. Учебно-познавательная деятельность |
||
|
Изучение нового материала |
||
|
Цель деятельности |
Совместная деятельность |
|
|
|
2 |
|
|
Ввести понятия ромба, квадрата, рассмотреть свойства и признаки этих фигур |
(Ф) 1. Введение понятия ромба. Рисунок и записи на доске и в тетрадях учащихся: ABCD — ромб, если ABCD — параллелограмм и АВ = ВС = CD = Т. — Верно ли утверждение: «Четырехугольник, у которого все стороны равны, является ромбом»? (Г[Ф) 2. Свойства ромба, признак ромба. — Перечислите все свойства ромба как частного вида параллелограмма. Выясните, каким еще свойством обладают диагонали ромба, кроме того, что они точкой пересечения делятся пополам. (Работа в группах с послеДующим обсуждением свойства Диагоналей ромба.) На доске и в тетрадях записать: Свойства ромба (рис. 9): Если ABCD — ромб, то:
г) АО = ОС, ВО = О»,
е) АО, ВО, СО, DO — биссектрисы углов А, В, С, D. (Г/Ф) — Сформулируйте утверждение, обратное особому свойству ромба, и выясните его справедливость. (Работа в группах с последующим обсуждением.) 3. Определение квадрата.
Рис. 10 Рис. П ABCD — квадрат, если ABCD — прямоугольник, АВ = ВС = CD = Т. — Верно ли утверждение: «Ромб, у которого все углы прямые, является квадратом»? — Верно ли утверждение: «Параллелограмм, у которого все стороны и все углы равны, является квадратом»? |
Рис. 8 D Рис. 9 |
Окончание
|
|
2 |
|||
|
|
4. Свойства квадрата, признаки квадрата. — Перечислите свойства квадрата, учитывая, что квадрат — это частный случай прямоугольника и ромба. Записать на доске и в тетрадях: Свойства квадрата: а) АВ CD=AD•, АВ СД ВС ll АО, 6) И = х-в = О = 900 в) ВО = ОС = 0D = АО, BD |
|||
|
Закрепление изученного материала |
||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
|
|
Закрепить полученные знания |
(Ф/И) 1. Решить задачу № 406. (И) 2. Решить самостоятельно № 407 |
дано: ABCD - ромб, = 60 0 , 10,5 см. Найти: PABCD. Решение: ZB = 600 , АВ = ВС (так как АВ и ВС — стороны ромба), тогда ZBAC = ZBCA = 60 0 , то есть ДАВС — равносторонний и АВ = АС = 10,5 см. У ромба все стороны равны, поэтому РАЖУ) АВ=4 • 10,5 = 42 (см). Ответ: 42 см. Решение: ZABC = 45 0 . BD — диагональ и биссектриса ZABC. ИЮ = 45 0 : 2 = 22 0 30' Из ДАВО (ZO = 90 0 , так как диагонали ромба перпендикулярны): ZOAB = 90 0 - 22 0 30' = 67 0 30' ответ: 22 0 30', 67 0 30' |
В
D |
Рис 12 |
|
III этап. Итоги |
урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
|||
|
|
|
|||
|
— Что нового узнали на уроке? — Какой этап урока оказался для вас самым сложным? — Оцените свою работу на уроке |
(И) Домашнее задание: п. 47 прочитать; решить № 412, 413 |
|||
|
Цель деятельности учителя |
Создать условия для закрепления теоретического материала по теме «Прямоугольник. Ромб. Квадрат»; для совершенствования навыков ешения задач по данной теме |
|||||
|
Те мины и понятия |
Ромб, квад ат, диагонали, углы |
|||||
|
Планируемые результаты |
||||||
|
П едметные умения |
Универсальные учебные действия |
|||||
|
Умеют работать с геометрическим текстом, точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики |
Познавательные: умеют выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки, устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение и выводы. Регулятивные: осознают важность и необходимость знаний для человека; проявляют познавательный интерес к изучению предмета. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками, работать в паре. Личностные: умеют контролировать процесс и результат учебной математической деятельности |
|||||
|
Организация пространства |
||||||
|
Фо мы аботы |
Ф онтальная (Ф); индивидуальная (И); групповая (Г) |
|||||
|
Образовательные ресурсы |
• Учебник. • Задания для индивидуальной работы |
|||||
|
1 этап. Самостоятельная работа по тео ии |
||||||
|
Цель деятельности |
Задания для самостоятельной аботы |
|||||
|
Проверить уровень усвоения теоретического материала |
(И/Ф) Проверка теоретического материала. — Заполните таблицу, используя знаки «+» (да) и «—» (нет). (Один из учащихся работает на переносной Доске, остальные в тетраДях. После завершения работы класс проверяет работу, выполненную на Доске.) Правильные ответы: |
|||||
|
|
Параллело амм |
Прямо- ГОЛЬНИК |
Ромб |
Квадрат |
||
|
Противоположные стороны параллельны и равны |
|
|
|
|
||
|
Все стороны авны |
|
|
|
|
||
|
П тиволежащие углы авны; сумма углов, п илежащих к одной сто оне, равна l800 |
|
|
|
|
||
|
Все углы прямые |
|
|
|
|
||
|
Диагонали пересекаются и точкой пересечения делятся пополам |
|
|
|
|
||
|
Диагонали авны |
|
|
|
|
||
|
Диагонали взаимно перпендикулярны и являются биссектрисами углов |
|
|
|
|
||
|
(После самопроверки учащиеся оценивают себя.) |
||||||
Окончание
|
П этап. Тест |
||
|
Цель деятельности |
Задания для самостоятельной работы |
|
|
Проверить уровень усвоения теоретического материала |
(И) Тесты в двух вариантах в распечатанном виде раздаются учащимся (см. Ресурсный материал). Ответы нужно записать в тетрадях, после чего учащиеся проверяют себя по заранее подготовленным ответам на обороте доски (или на экране компьютера), выставляют оценки |
|
|
III ЭпИ. Самостоятельная работа |
||
|
Цель деятельности |
Задания для самостоятельной работы |
|
|
Проверить умение применять теоретические знания при решении задач |
(И) При выполнении работы учитель контролирует работу менее подготовленных учащихся, оказывая при этом необходимую индивидуальную помощь. По окончании работы проводится самопроверка. Самопроверку можно организовать следующим образом: заранее подготовить решение на листочках и по окончании работы раздать листочки ученикам для проверки и исправления ошибок. 1. Найдите углы ромба, если его диагонали составляют с его стороной углы, один из которых на 30 0 меньше другого.
ИВО = 300 , ZBAO = 60 0 , а так как диагонали ромба являются биссектрисами его углов, то ZBAD —- 1200 , ЛВС = 60 0 . Поскольку противолежащие углы в ромбе равны, то ZADC = ZABC = 600 , ZBCD = ZBAD = 120 0 . ответ: 60 0 , 120 0 , 600 , 120 0 . 2. Угол между диагоналями прямоугольника равен 80 0 . Найдите углы между диагональю прямоугольника и его сторонами. АС Диагонали прямоугольника равны и точкой пересечения делятся пополам, значит ВО = 2 2 и МОВ — равнобедренный, тогда ZOAB = ZOBA = 500 . В прямоугольнике все углы прямые, тогда: ZOAD = ZBAD — ZOAB = 90 0 — 50 0 = 40 0 . Ответ: 50 0 , 40 0 |
|
|
IV этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
Какой этап урока оказался для вас самым сложным? — Оцените свою работу на уроке |
(ИТ) Домашняя работа: № 426, 427. Класс делится на две группы. Задание для групп: работая с энциклопедиями и справочниками, пользуясь возможностями Интернета, найти ответы на один из поставленных вопросов: 1. Что называется симметрией, и когда это понятие возникло? 2. Существует ли симметрия в окружающем нас мире? |
|
Вариант 1 1 . Любой
прямоугольник является.![]()
а) ромбом;
б) квадратом;
в) параллелограммом;
г) нет правильного ответа.
2. Если в четырехугольнике диагонали перпендикулярны, то этот четырехугольник — ...
![]()
а) ромб;
б) квадрат;
в) прямоугольник;
г) нет правильного ответа.
З. Ромб — это четырехугольник, в котором.![]()
а) диагонали точкой пересечения делятся пополам и равны;
б) диагонали взаимно перпендикулярны и точкой пересечения делятся пополам;
в) противолежащие углы равны, а противолежащие стороны параллельны;
г) нет правильного ответа. Ответы — в; 2— г; 3 —6.
Вариант П 1. Любой ромб
является.![]()
а) квадратом;
б) прямоугольником;
в) параллелограммом;
г) нет правильного ответа.
2. Если в параллелограмме диагонали перпендикулярны, то этот параллелограмм — ...
а) ромб;
б) квадрат;
в) прямоугольник;
г) нет правильного ответа.
З. Прямоугольник — это четырехугольник, в котором. . .
а) противолежащие стороны параллельны, а диагонали равны;
б) диагонали точкой пересечения делятся пополам и являются биссектрисами его углов;
в) два угла прямые и две стороны равны;
г) нет правильного ответа. ![]() Ответы:
— в; 2 — а; З — а.
Ответы:
— в; 2 — а; З — а.
Урок 12. Тема: ОСЕВАЯ И ЦЕНТРАЛЬНАЯ СИММЕТРИЯ
|
Цель деятельности чителя |
Создать условия для введения понятий осевой и центральной симметрий |
||
|
Те мины и понятия |
Ось симме ии, цент симме ии, симмет ичные |
и ы |
|
|
Плани емые ез льтаты |
|||
|
П едметные мения |
Униве сальные чебные действия |
||
|
Умеют работать с геометрическим текстом, точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики
|
Познавательные: умеют выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки, устанавливать причинно-следственные связи, строить логическое рассуждение, делать умозаключения и выводы. Регулятивные: умеют контролировать процесс и результат учебной математической деятельности. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками, умение работать в паре. Личностные: п оявляют познавательный инте ес к из чению п едмета |
||
![]() ПроДол.ж•ение
ПроДол.ж•ение
|
|
О ганизация п ост анства |
|
|
Фо мы аботы |
Ф онтальная Ф ; индивид альная (И |
|
|
Образовательные ес сы |
• Учебник. • Сведения об осевой и цент альной симмет ии |
|
|
|
этап. П ове ка домашней аботы |
|
|
Цель деятельности |
Деятельность чителя |
Деятельность ащихся |
|
Выявить трудности, возникшие у учащихся при выполнении домашнего задания |
— Каждая группа, работая с энциклопедиями и справочниками, пользуясь возможностями Интернета, должна была найти ответы на один из поставленных вопросов: 1. Что называется симметрией, и когда это понятие возникло? 2. С ществ ет ли симмет ия в ок жающем нас ми е? |
(См. Ресурсный материал.) |
|
|
П этап. Из чение новой темы |
|
|
ель деятельности |
Деятельность чителя |
еятельность чащихся |
|
Научиться строить фигуры, симметричные относительно прямой и относительно точки |
(ФМ) 1. Работа с учебником. Прочитайте п. 48 учебника на с. 1 10—1 1 1, ответьте на вопросы: 1 ) Какие две точки называются симметричными относительно прямой? 2) Какая фигура называется симметричной относительно данной прямой? 3) Какие две точки называются симметричными относительно данной точки? 4) Какая фигура называется симметричной относительно данной точки? 2. Практическая работа. Учитель объясняет как строить фигуру, симметричную относительно п ямой и относительно точки |
|
|
|
III этап. Зак епление пол ченных знаний |
|
|
|
Пе вичная п ове ка понимания |
|
|
ель деятельности |
еятельность чителя |
еятельность аЩИХСЯ |
|
Выяснить степень понимания того, что такое ось симметрии, центр симметрии |
№ 417 (устно). № 418 (устно). Какие из следующих букв имеют ось симметрии: А, Б, Г, Е, О, Р? № 422 (устно). Имеют ли центр симметрии: а) отрезок, б) луч, в) пара пересекающихся прямых; г) квадрат? № 423 (устно). Какие из следующих букв имеют центр симмет Ии: А, О, М, Х, К? |
.N2 417. а) две; б) бесконечно много; в) одну. ЛЬ 418. А, Е, О. N2 422. а) да; б) нет; в) да; г) да. ЛЕ ОЗ. О их |
|
Цель деятельности учителя |
Создать условия для закрепления теоретического материала по теме «Прямоугольник. Ромб. Квадрат», совершенствования навыков решения задач по данной теме, подготовки учащихся к контрольной работе |
|
|
Термины и понятия |
Ромб, квадрат, диагонали, углы |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
|
2 |
|
|
У меют работать с геометрическим текстом, точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики |
Познавательные: умеют выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных и познавательных задач. Регулятивные: принимают и сохраняют учебные задачи. |
|
![]() Окончание
Окончание
|
Первичное закрепление. Самостоятельная практическая работа |
||
|
Цель деятельности |
Задания для самостоятельной работы |
|
|
Проверить практические навыки в построении симметричных фигур |
Проверка. Учащиеся демонстрируют построения на доске с комментированием. (И) № 416. Даны две точки А и В, симметричные относительно некоторой прямой, и точка М. Постройте точку, симметричную точке М относительно той же прямой. № 421. Даны точки А, В, и М. Постройте точку, симметричную точке М относительно середины отрезка АВ |
|
|
IV этап. Итоги урока. Рефлексия |
||
|
Деятельность чителя |
Деятельность чащихся |
|
|
— Какой этап урока вызвал наибольшее затруднение и почему? — Составьте синквейн по данному уроку |
(И) Домашнее задание: придумайте рисунок для вышивки, используя или осевую, или центральную симметрию |
|
Симметрия является фундаментальным свойством природы, представление о котором, как отмечал академик В. И. Вернадский (1863—1945), «слагалось в течение десятков, сотен, тысяч поколений». Изучение археологических памятников показывает, что человечество на заре своей культуры уже имело представление о симметрии и осуществляло ее в рисунке и в предметах быта. Первоначальное понятие геометрической симметрии — это гармония пропорций, соразмерность, что и означает в переводе с греческого слово «симметрия».
Симметрией обладают не только геометрические фигуры или вещи, сделанные рукой человека, но и многие творения природы (бабочки, стрекозы, листья, морские звезды, снежинки и т. д.). Особенно разнообразны свойства симметрии кристаллов. Большинство растений и животных симметричны. Симметрия живых организмов и растений целиком обусловлена воздействием внешней среды, которая принимает самое активное участие в формировании внешнего облика обитателей нашей планеты.
Урок 13. Тема: РЕШЕНИЕ ЗАДАЧ
|
|
|
2 |
||
|
|
|
Коммуникативные: умеют находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов. Личностные: проявляют способность к эмоциональному восприятию математических объктов, задач, ешений, асс ждений |
||
|
|
О ганизация п ост анства |
|||
|
Фо мы аботы |
Ф онтальная (Ф ; индивид альная (И |
|||
|
Образовательные ес сы |
Учебник. • Задания для математического диктанта, самостоятельной аботы |
|||
|
|
этап. Ак ализация опо ных знаний |
|||
|
|
Математический диктант |
|||
|
ель деятельности |
Задания для самосл оятельной аботы |
|||
|
Проверить уровень теоретической подготовки |
(И) После проведения диктанта осуществляется взаимопроверка. 1. Является ли прямоугольником параллелограмм, у которого есть прямой угол? (Да.) 2. Обязательно ли является прямоугольником четырехугольник, у которого есть прямой угол? (Нет.) З. Верно ли, что каждый прямоугольник является параллелограммом? (Да.) 4. Верно ли, что каждый параллелограмм является прямоугольником? (Нет.) 5. Диагонали прямоугольника АЕКМ пересекаются в точке О. Отрезок АО = 3. Найдите длину диагонали ЕМ. (б.) 6. Диагонали параллелограмма равны 3 и 5 дм. Является ли этот параллелограмм прямоугольником? (Нет.) 7. Диагонали четырехугольника равны. Обязательно ли этот четырехугольник прямоугольник? (Нет.) 8. Сумма длин диагоналей прямоугольника 13 см. Найдите длину каждой диагонали. (6,5.) 9. Периметр ромба равен 12 см. Найдите длины его сторон. (З см.) 10. Верно ли, что каждый ромб является параллелограммом? (Да.) 11. Верно ли, что каждый параллелограмм является ромбом? (Нет.) 12. Ромб ABCD имеет прямой угол. Является ли этот ромб квадратом? (Да.) 13. Две соседние стороны параллелограмма равны и образуют прямой угол. Как называется такой параллелограмм? (КваДрат.) 14. иагонали квад ата делят его на четы е е голышка. Найдите глы каждого т е гольника. (45 0. |
|||
|
|
П этап. Решение задач |
|||
|
Цель деятельности |
еятельность чителя |
еятельность чащихся |
|
|
|
Выработать умение применять теоретические знания при решении задач |
(Г) 1. Решение задач № 428, 434, 438. 2. Защита решений |
Г•Г2 428. Решение: 1) DP — биссектриса Zl = Z2. 2) Zl = Z3, как внутренние накрест лежащие при ВС llAD и секущей PD. Имеем Z1 = Z2 = Z3. 3) Аналогично для биссектрисы угла В имеем 9
|
|
|
|
|
2 |
З |
|
|
|
4) но ЛВС = UDC, поэтому д = П = Z3 = д = Z5 = Z6. Z5 и Z3 соответственные при прямых PD и ВК и секущей ВС PD ВК. 5) Аналогично доказывается, что АМ АС. 6) STQR — параллелограмм по определению. 7) ДРО — равнобедренный, так как Z3 = П, CQ — биссектриса и высота. 8) В параллелограмме STQR один угол прямой он является прямоугольником.
дано: ABCD - ромб, АС = О. Доказать: оМ- ОЕ = ор. Доказательство: 1) Рассмотрим ABON и ДВОМ: ВО — общая, Рис. 2 ZNBO = ZMBO (свойство ромба), следовательно, ДВОЛ,Т = АВОМ (по гипотенузе и острому углу). Отсюда ОМ = 0N (по определению равенства треугольников). 2) Аналогично через AFOD = ДЕО имеем ОЕ = 0F. З) Рассмотрим МОЕ и АСОМ: АО = ОС (свойство ромба), ZOAF = ZOCM (свойство ромба), следовательно, МОЕ = АСОМ (по гипотенузе и острому углу), следовательно, 0F = ОМ (по определению равенства треугольников). 4. В ы вод: ОМ = ОЛТ (из п. 1), ОЕ= 0F (из п. 2), 0F= ОМ (из п. З), следовательно, ОМ = ОМ= ОЕ = OF.
Дано: ABCD — трапеция,АС СД ZBAC = Z СО, АВ( П = 20 см, О = 60 0 . Найти: АД Рис. З |
|
|
2 |
З |
|
|
|
Решение: 1) Рассмотрим ДАСТ ZC = 90 0 , ZD = 60 0 , следовательно, ZA = 30 0 , значит,
2 2) Так как ZBAC = ZCAD - 30 0 , значит, ABCD — равнобедренная трапеция, CD=AB. 3) Так как ZCAD =ZBAC, следовательно, ZBAC = ОСА, следовательно, ЛАВС — равнобедренный, АВ = ВС. 4) = АВ + ВС + CD+AD. Так как —0, а АВ = ВС = СД то: 2 20 = —0+ —AD +—AD+AD. 2 2 2 20 = 2,50; AD = 20 : 2,5; О = 8 (см). Ответ: 8 см |
|
III этап. Самостоятельная работа |
||
|
Цель деятельности |
Задания для самостоятельной работы |
|
|
Закрепить теоретические знания и практические умения при решении задач |
(И) Ва риант 1 . Через точку пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая стороны AD и ВС соответственно в точках Е и Е. Найдите стороны параллелограмма, если его периметр равен 28 см, АЕ = 5 см, BF = 3 см. Ответ: би 8 см. 2. Найдите меньшую боковую сторону прямоугольной трапеции, основания которой равны 1 0 см и 6 см, а один из углов равен 45 0 . От в ет: 4 см. 3. Разделите данный отрезок на 5 равных частей (Длину отрезка учитель опреДеляет сам). Вариант П 1. Биссектрисы углов А и D параллелограмма ABCD пересекаются в точке М, лежащей на стороне ВС. Найдите стороны параллелограмма, если его периметр равен 36 см. Отв ет: би 12 см. 2. Найдите боковую сторону равнобедренной трапеции, основания которой равны 12 см и 6 см, а один из углов равен 120 0 . Ответ: 6 см. З. Разделите данный отрезок на б равных частей (Длину отрезка учитель определяет сам) |
|
Окончание
|
IV этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
— Какой этап урока был для вас самым сложным? Почему? — Оцените свою работу. — Какие вопросы у вас еще остались? |
(И) Домашнее задание: подготовиться к контрольной работе. Решить задачи. . В ромбе ABCD Z D = 1400 . Определите углы треугольника AOD (О — точка пересечения диагоналей). 2. На диагонали МР прямоугольника MNPQ отложены равные отрезки МА и РВ. Докажите, что ANBQ — параллелограмм.
3. В с |
|
Урок 14. Тема.• КОНТРОЛЬНАЯ РАБОТА N2 1
|
Цель деятельности чителя |
Создать условия для проверки знаний, умений и навыков учащихся по усвоению и применению изученного материала |
|
|
Те мины и понятия |
Ромб, квад ат, диагонали, углы, па аллелограмм, трапеция |
|
|
Планируемые езультаты |
||
|
П едметные мения |
Универсальные учебные действия |
|
|
Умеют демонстрировать знание основных понятий, применять полученные знания деля решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности |
Познавательные: проводят сравнение, сериацию и классификацию по заданным критериям. Регулятивные: вносят необходимые коррективы в действие после его завершения на основе его учета характера сделанных ошибок; осуществляют самоанализ и самоконтроль. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: осознают важность и необходимость математических знаний для человека |
|
|
Организация п остранства |
||
|
Фо мы аботы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные ес сы |
• Учебник. • Задания для контрольной работы |
|
|
этап. Выполнение контрольной работы |
||
|
Цель деятельности |
Задания для кон ольной аботы |
|
|
|
2 |
|
|
Определить степень усвоения учебного |
Вариант 1 1. Диагонали прямоугольника ABCD пересекаются в точке О. Найдите угол между диагоналями, если ИВО = 30 |
|
Окончание
|
|
2 |
|
|
материала, уровень развития умения решать задачи |
2. В параллелограмме kMNP проведена биссектриса угла МКР, которая пересекает сторону в точке Е. а) Докажите, что треугольник КМЕ равнобедренный. б) Найдите сторону КР, если МЕ = 10 см, а периметр параллелограмма равен 52 см. Вариант II . Диагонали ромба КАТР пересекаются в точке О. Найдите углы треугольника КОМ, если ZMNP = 800. 2. На стороне ВС параллелограмма ABCD взята точка М так, что АВ = ВМ. а) Докажите, что АМ — биссектриса угла ВАД б) Найдите периметр параллелограмма, если CD = 8 см, СМ = 4 см. Вариант III 1. Через вершину С прямоугольника ABCD проведена прямая, параллельная диагонали BD и пересекающая прямую АВ в точке М. Через точку М проведена прямая, параллельная диагонали АС и пересекающая прямую ВС в точке N. Найдите периметр четырехугольника АСЛТ, если диагональ BD равна 8 см. 2. Биссектрисы углов А и D параллелограмма ABCD пересекаются в точке М, лежащей на стороне ВС. Луч DM пересекает прямую АВ в точке N. Найдите периметр параллелограмма ABCD, если AN= 10 см |
|
|
|
II этап. Итоги урока |
|
|
|
Деятельность учителя |
Деятельность учащихся |
|
|
|
Домашнее задание: повторить материал гл. 1, S 4, с. 13—16 |
ГЛАВА VI. ПЛОЩАДЬ
Урок 15. Тема: ПЛОЩАДЬ МНОГОУГОЛЬНИКА
|
Цель деятельности чителя |
Создать условия для представления об измерении площадей многоугольников, рассмотрения основных свойств площадей и выведения о м лы для вычисления площади квад ата |
|
|
Те мины и понятия |
Равновеликие много гольники, авносоставленные много гольники |
|
|
Плани емые ез льтаты |
||
|
П едметные мения |
Униве сальные чебные действия |
|
|
Владеют базовым понятийным аппаратом по основным разделам содержания; имеют представление об основных изучаемых понятиях |
Познавательные: умеют выбирать и создавать алгоритмы для решения математических проблем. Регулятивные: умеют самостоятельно ставить цели, адекватно оценивать правильность или ошибочность выполнения учебной задачи. Коммуникативные: умеют находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов. Личностные: имеют целостное мировоззрение, соответствующее современному уровню азвития на ки и общественной п актики |
|
Продолжение
|
|
Организация пространства |
|
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные ресурсы |
• Учебник. • Задания для фронтальной и индивидуальной работы |
|
|
|
этап. Анализ ошибок, допущенных в контрольной работе |
|
|
|
П этап. Подготовка к восприятию нового материала |
|
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
Подготовить учащихся к восприятию понятия площади многоугольника |
(Ф) Решить задачи: 1. Через точку во внутренней области равностороннего треугольника проведены две прямые, параллельные двум сторонам треугольника. На какие фигуры разбивается этими прямыми данный треугольник? 2. Дано: ABCD — параллелограмм, AD = ИВ, АМ— биссектриса Z ВАД Докажите, что часть отрезка АМ, лежащая во внутренней области параллелограмма ABCD, равна части, лежащей во внешней области |
Доказательство: . ДАТ— равнобедренный (АВ = ВЛО. Рис. 1 2. ZDAN = ZANB (накрест лежащие); ZANB = Z№WC (вертикальные). З. так как Ж) = ИВ, то NC. 4. ZABN= ZMCN (накрест лежащие). 5. ДАВЛГ = &VCN (по П признаку), значит, AN= NM |
|
|
III этап. Изучение новой темы |
|
|
Цель деятельности |
Совместная деятельность |
|
|
|
2 |
|
|
Ввести понятие площади многоугольника |
(Ф) 1. Ввести понятие площади. — Понятие площади каждому известно из жизненного опыта. Часто мы слышим: «площадь нашей квартиры равна 60 м ». Как вы понимаете это предложение? (Это величина квартиры. Пол Данной квартиры можно застелить 60 кваДратаии со стороной 1 м.) — С сегодняшнего дня мы будем учиться вычислять площади различных геометрических фигур. 2. Определить единицы измерения площадей.
— Как вы понимаете утверждение «единица измерения площади см »? (ПлощаДь измеряется квадратами со стороной 1 см.) Может ли площадь фигуры выражаться отрицательным числом? (Нет, не может.) З. Дать представление об измерении площадей многоугольников способом разбиения фигуры на квадраты. |
|
Продолжение
|
|
2 |
|||||||||||||||||
|
|
— Как измерить площадь фигуры, изображенной на рис. 2 в квадратных дециметрах? (Нужно разбить фигуру на кваДратные Дециметры.) — Сторону AD разобьем на отрезки по 1 дм каждый и через концы отрезков проведем прямые, перпендикулярные стороне О. Далее проведем прямые, параллельные АД на расстоянии I дм друг от друга (рис. З.). Сосчитаем количество целых квадратов, вместившихся в фигуру ABCD. Неполные квадраты разобьем на квадратные сантиметры. Каждый квадратный сантиметр — это сотая часть квадратного дециметра. Таким образом, можно вычислить площадь фигуры в дм с точностью до 0,01 дм . Для более точного измерения площади данной фигуры неполные квадраты со стороной I см разобьем на квадраты со стороной 1 мм, и т. д.
— Такой способ вычисления площадей фигур называется способом разбиения фигуры на квадраты. Но чаще всего площади геометрических фигур вычисляются по готовым формулам, с которыми мы познакомимся на следующих уроках. 4. Рассмотреть свойства площадей. а) Равные многоугольники имеют равные площади. б) Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников. в) Площадь квадрата равна квадрату его стороны. (Доказательство третьего свойства является трудным, поэтому п. 49 можно преДложить более подготовленным учащимся изучить самостоятельно.) |
|||||||||||||||||
|
IV этап. Закрепление изученного материала |
||||||||||||||||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
||||||||||||||||
|
На примере устных задач и простых задачах отработать понятие площади |
(Ф/И) Решите задачи (устно): 1 . ABCD — параллелограмм. SABCI) 12. Найти: SABI), SB('D. 2. ABCD — прямоугольник. CE=DE , SАВ(Ч) — Q• Найти: SABF. |
В
|
Рис. 4
Рис. 5 |
1. 6 и 6. 2. SABF— |
||||||||||||||
|
Цель деятельности чителя |
Создать условия для выведения формулы площади прямоугольника |
|
|
|
Те мины и понятия |
Равновеликие много гольники, авносоставленные много голышки, площадь квад ата, площадь п ямо голышка |
|
|
|
Плани емые ез льтаты |
|
||
|
П едметные мения |
Униве сальные чебные действия |
|
|
|
|
2 |
|
|
|
Владеют базовым понятийным аппа атом по основным |
Познавательные: меют выби ть и создавать алго итмыддя ешения математических |
блем. |
|
Окончание
|
|
2 |
3 |
||
|
|
Рис. б
Рис. 7 5. Решить на доске и в тетради № 449 (в), 450 (в). К доске вызываются двое учеников. После выполнения заданий осуществляется проверка. 6. Самостоятельно решить № 449 (а), 450 (а), 451, 447 |
з. 13,5. 4. 9 + 4 = 13. Л) 449 (в).
12, 449 (а). 1,44 см 2 ЛР2 450 (а). 4 СМ. .N2 451 (а). 24 см 2 = 24 • 100 .N2 451 (6 . 24 см 2 = 24 • 0,01 |
18 (м2). мм 2 = 2400 мм 2. 2 дм= 0,24 дм 2 |
|
|
V этап. Итоги ока. Ре лексия |
||||
|
еятельность чителя |
еятельность чащихся |
|||
|
— Составьте синквейн к уроку. — Что нового знали на оке? |
(И) Домашнее задание: п. 49, вопросы 1, 2; решить задачи № 448, 449 (б), 450 |
|||
Урок 16. Тема: ПЛОЩАДЬ МНОГОУГОЛЬНИКА
Продолжение
|
|
2 |
||||||
|
разделам содержания; имеют представление об основных изучаемых понятиях |
Регулятивные: умеют самостоятельно ставить цели, адекватно оценивать правильность или ошибочность выполнения учебной задачи. Коммуникативные: умеют находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов. Личностные: имеют целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики |
||||||
|
Организация пространства |
|||||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
||||||
|
Образовательные ресурсы |
• Учебник. • Задания для фронтальной и индивидуальной работы |
||||||
|
этап. Проверка домашнего задания |
|||||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|||||
|
Выявить трудности, возникшие у учащихся при выполнении домашней работы |
(Ф) 1. Ответить на вопросы учащихся. 2. Проверить решение № 448 |
№ 448. Решение: Опустим перпендикуляр к ВС из точки Е (ЕО Ш ВС).В Прямоугольные треугольники АВМ и ЕОМ равны по гипотенузе и острому углу (АМ= ЕМ,
Рис. ЕО CD, так как в прямоугольнике противолежащие стороны АВ и CD равны. Прямоугольные треугольники EON и DCN равны по катету и острому углу (ЕО = CD, ZONE = ZCND, как вертикальные).
Д.МОЕ = ДМВА &VOE = ANCD Тогда SAI,7)
|
|||||
|
этап. Изучение нового материала |
|||||||
|
Цель деятельности |
Совместная деятельность |
||||||
|
|
2 |
||||||
|
Доказать формулу площади прямоугольника |
(Ф/И) Выполните задания: I . Докажите, что два прямоугольника равны, если равны их смежные стороны. |
||||||
|
|
2 |
|||||
|
|
2. АВСД - квадрат, Мм П АД ЕЕ и ВС. D Найдите площадь четырехугольника AFkM, если АМ = СЕ= З см, см м в Рис. 2 З. Доказать теорему о площади прямоугольника. (ПоДготовить чертеж заранее, см. учебник, рис. 181.) |
|||||
|
III этап. Закрепление изученного материала |
||||||
|
цель деятельности |
Деятельность учителя |
Деятельность учащихся |
||||
|
Отработать умение применять формулу площади прямоугольника |
(ФМ) 1. Решить № 452 (а, в), 453 (в) (устно). 2. Решить задачу № 458 на доске и в тетрадях учащихся. Один из учащихся решает задачу у доски, остальные в тетрадях |
ЛЕ 458.
Заборы имеют одинаковую длину, поэтому участки земли имеют одинаковыЙ периметр. - аь = 220 • 160 = 35 200 (м2 ) прям пряч -2 • (а + (220+ Рке= 4а, но Кв = Рпряи = 760 (м), то есть 4а = 760, а = 190
(м) 36 100 м 2 > 35 200 м 2 , поэтому площадь квадрата больше площади прямоугольника. 36 100-35 200 = 900 (м2) От в е т : площадь участка земли, имеющего форму квадрата, больше г на 900 м |
||||
|
IV этап. Самостоятельная работа |
||||||
|
Цель деятельности |
Задания для самостоятельной работы |
|||||
|
|
2 |
|||||
|
Закрепить полученные знания |
(И) Самостоятельная работа (5—7 минут) с последующей самопроверкой. 1 . Найдите площадь прямоугольника, если его периметр равен 80 см, а отношение сторон равно 2 : 3. Решение: х — коэффициент пропорциональности. |
|||||
|
Цель деятельности учителя |
Создать условия для выведения формулы площади параллелограмма |
|
|
Термины и понятия |
Равновеликие многоугольники, равносоставленные многоугольники, площадь квадрата, площадь прямоугольника, площадь параллелограмма |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
|
2 |
|
|
Владеют базовым понятийным аппаратом; умеют работать с геометрическим текстом |
Познавательные: умеют устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение. Регулятивные: умеют адекватно оценивать правильность или ошибочность выполнения учебной задачи. |
|
Окончание
|
|
2 |
|
|
|
АВ- 16 см, О 24 см. S=16 • 24 = 384 (см 2 ) Ответ: 384 см 2. Рис. З
Ответ: 64 см 2 , 32 см Рис. 4 |
|
|
V этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф) — Что нового узнали на уроке? — Сформулируйте З вопроса по сегодняшней теме |
(И) Домашнее задание: вопрос З, с. 133; № 452 (б, г), 453 (а, б), 448. Вырезать из бумаги два равных прямоугольных треугольника и составить из них: I ) равнобедренный треугольник; 2) прямоугольник; З) параллелограмм, не являющийся прямоугольником; 4) равновеликие фигуры |
|
Урок 17. Тема: ПЛОЩАДЬ ПАРАЛЛЕЛОГРАММА
|
|
|
2 |
|
|
|
Коммуникативные: умеют находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, ешений, асс ждений |
|
|
О ганизация п ост анства |
|
|
Фо мы аботы |
Ф онтальная (Ф ; индивид альная (И); г пповая (Г |
|
|
Образовательные ес сы |
• Учебник. • Задания для индивид альной, онтальной аботы |
|
|
|
этап. Акт ализация опо ных знаний |
|
|
Цель деятельности |
Совместная деятельность |
|
|
Проверить правильность выполнения домашнего задания, подготовить учащихся к восприятию новой темы |
(И) К доске вызываются три ученика для оформления решения домашних задач. В это время учитель проводит теоретический опрос, 3—6 учащихся работают по индивидуальным карточкам. После теоретического опроса проверяют правильность решения домашнего задания. Теоретический опрос. — Перечислите основные свойства площадей. — Сформулируйте и докажите теорему о площади прямоугольника. Работа по карточке. 1. Периметр квадрата равен 20 см. Прямоугольник имеет такую же площадь, что и квадрат, а одна из его сторон равна 10 см. Найдите периметр прямоугольника. 2. Найдите площадь прямоугольника с периметром 60 см и отношением сторон 1 : 2. Решение задач:
А Рис. 2. дано: ABCD -параллелограмм. Найти: SABCD. |
|
|
П этап. Изучение нового материала |
|
|
Цель деятельности |
Совместная деятельность |
|
Доказать формулу для вычисления площади параллелограмма |
(Ф) 1. Ввести понятие высоты параллелограмма. На доске и в тетрадях — рисунок.
Рис. З ВН— высота, проведенная к стороне AD параллелограмма ABCD. ВК— высота, проведенная к стороне CD параллелограмма ABCD. (Г/Ф) 2. Задача. Дано: ABCD — параллелограмм, AD = а, ВН— высота, ВН= h. Найти: SABCD• (Разбить учащихся на группы по 3—4 человека, Дать на обдумывание 3—5 минут, а затем обсуДить решение задачи, выслушав все варианты и выбрав среди предложенных наиболее удачный. Решение заДачи оформляется в виде теоремы на Доске и в тетраДях. У доски работает один из наиболее подготовленных учащихся.) Теорема: S = а • ha, где а — сторона параллелограмма, ha — высота, проведенная к ней. А Рис. 4 Доказательство: 1) Проведем ВН О, СЕ О. 2) ЛАВН= ОСЕ по гипотенузе и острому углу (АВ = CD, как противолежащие стороны параллелограмма; Zl = П, так как Z2 = 80 0 — ZADC и Zl + Z2 = 1 80 0 , как сумма внутренних односторонних углов при параллельных прямых АВ и CD и секущей АО, ZAHB = ZCED = 90 0 ) S„н = S l)CE, DE=AH. З) SABC.D = SABH + SIIBCD S + SHBCD —
SHD(E. НВСЕ — прямоугольник, SHB(7.: —- НЕ ВН•, НЕ = Ю) + DE, но так как DE =
АН, то НЕ = АН + Ю = О, то есть |
табл.
|
III этап. Закрепление изученного материала |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
На простых задачах отработать применение формулы площади параллелограмма |
(Ф) Решить задачи: № 459 (а) (устно), 459 (б, в), 464 (в) (устно) |
|||
|
Самостоятельная работа |
||||
|
Задания для самостоятельной работы |
||||
|
Вариант 1 Стороны параллелограмма 10 см и 6 см, а угол между этими сторонами 1500 . 1. 2. Катет АЕ лежит против угла 30 0 , поэтому АЕ = 0,5АВ = 3 см. АВСЮ - вс .АЕ= 10 • з = зо (см 2 ). 6 Вариант П Острый угол параллелограмма равен 300 , а высоты, проведенные из вершины параллелограмма. 1. Катет ВМ лежит против угла в 30 0 , поэтому АВ = 2ВМ= 6 см. 2. = ВК. DC=8 6=48 (см 2 ). Вариант III Найдите площадь ромба, диагонали которого равны 8 см и 6 см. Использовать задание З из домашней
работы. ВО 2 S АКВО. = з . 12 (см). 2 12 • 2 = 24 (СМ). Организовать проверку, открыв доску с правшљным решением. ПоДвести учащихся к выводу, что площадь ромба равна половине произведения |
тупого в зоо его |
Найдите площадь
Рис. 5 угла,
Рис. 6
D рис. 7 Диагоналей |
этого параллелограмма.
D равны 8 см и З см. Найти площадь к |
|
|
Цель деятельности чителя |
Создать условия для выведения формулы площади треугольника |
||
|
Те мины и понятия |
Площадь квад ата, площадь п ямо гольника, площадь па аллелог амма, площадь т е гольника, авновеликие |
иг ы |
|
|
Плани емые ез льтаты |
|||
|
П едметные мения |
Униве сальные чебные действия |
||
|
Владеют базовым понятийным аппаратом; умеют работать с геометрическим текстом |
Познавательные: умеют устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение. Регулятивные: умеют адекватно оценивать правильность или ошибочность выполнения учебной задачи. Коммуникативные: умеют находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, ешений, рассуждений |
||
|
О ганизация п ост анства |
|||
|
Фо мы аботы |
Ф онтальная (Ф); индивид альная (И) |
||
|
Образовательные ес сы |
• Учебник. • Задания для индивид альной и онтальной аботы |
||
|
этап. П ове ка домашнего задания |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
|
2 |
||
|
Проверить уровень усвоения теоретического мате иала, |
(Ф/И) l . Теоретический опрос. — Сформулируйте и докажите теорему о площади параллелограмма. (Один ученик готовит Доказательство теоремы у доски.) —С о м ли йте основные свойства площадей иг |
||
Окончание
|
IV этап. Итоги |
ока. Ре лексия |
|
Деятельность учителя |
Деятельность чащлся |
|
(Ф) По каким формулам можно вычислить площадь параллелограмма и площадь ромба? — Что нового узнали на уроке? — Оцените свою работу |
(И) Домашнее задание: 2, вопрос 4, с. 133; № 459 (г), 460, 464 (б). По желанию: I . Найдите углы параллелограмма, если его площадь равна 20 см , а высота, проведенная из вершины тупого угла, делит одну из сторон на отрезки 2 см и 8 см, считая от вершины острого угла. От в ет : 45 0 ; 135 0 . 2. Сравните площади параллелограмма и прямоугольника, если они имеют одинаковые основания и одинаковые периметры. О т в е т : площадь п ямоугольника больше площади па аллелог амма |
Урок 18. Тема: ПЛОЩАДЬ ТРЕУГОЛЬНИКА
|
|
2 |
||
|
выявить трудности, возникшие у учащихся |
— Сформулируйте теорему о площади прямоугольника. 2. Решение задач с целью закрепления формулы для дующей самопроверкой.) 1) ABCD — параллелограмм. Найти: SABCD. А Рис. 3) ABCD— параллелограмм. Найти: SABCD.
Рис. З Ответы: 1) SABCD = 30 см2 ABCD — 20 СМ2; З) SABCD - 56 |
вычисления площади параллелограмма. (Самостоятельно с после- 2) ABCD -параллелограмм. Найти: SABCD.
Рис. 2
Рис. 4 см 2 ; 4) ABCD — 40 см2 |
|
|
П этап. Мотивация к деятельности |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Подготовить учащихся к восприятию новой темы |
(Ф/И) Решите следующие задачи (устно): . ABCD — параллелограмм. Найти: SABCl),
Рис. 5 В процессе решения этих задач необходимо повторить основные свойства раллелограмма, акцентируя внимание учащихся на том, что диагональ делит |
2. ABCD — параллелограмм. Найти: SABD.
Рис. 6 площадей, формулу для вычисления площади папараллелограмм на два равных треугольника. |
|
ПроДолжение
|
III этап. Изучение нового материала |
|||
|
Цель деятельности |
Совместная деятельность |
|
|
|
Вывести формулу площади треугольника |
(Ф) Задач а. Дано: в треугольнике АВС АВ = с, СН— высота, СН h. Найти: SABC. Учащиеся решают задачу самостоятельно, после обсуждения решения задачи и на доске записывается: ha • а : 2, где а — сторона треугольника, /1а — высота, проведенная к стороне Следствия 1 и 2 можно предложить в виде задач на доказательство по вариантам. вар и ант: В ЛАВС Z С = 90 0 . Докажите, что SAB(— АС • ВС. П вар и ант: В
треугольниках АВС и ЛПК высоты, проведенные к сторонам Докажите, ЧТО SABC :
SMNk Решения задач обсудить, в тетрадях и на доске начертить рисунки и выполнить СлеДствия теоремы о площаДи треугольника. 1. Soc= CA • св . 2
Рис. 8 2. Если ВНи NE-высоты ДАВС и ЛЛЛК соответственно и ВН- ЛЕ, то
Рис. 9а Рис. 96 |
в тетрадях А Н а. АВ и ДТ соответственно, равны. запись: = АС: МК МАК |
в Рис. 7
|
![]() Окончание
Окончание
|
IV этап. Решение задач |
||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
1 |
2 |
З |
|
При решении задач отработать формулу площади треугольника |
(Ф) 1. Решить устно задачи № 468 (а, б), 471, 474. К задаче № 474 заранее подготовить на доске рисунок. Отве ты к задачам: 2 № 468 77 см . № 468 (6). см 2 № 471 22 см 2 •, (6) дм 2 № 474. Площади равны. 2. Решить задачу № 470. Один из учащихся работает у доски, остальные — в тетрадях. З. Решить самостоятельно задачи № 472, 475 |
М 470. Я = 0,5а • • = 9 (см 2). 2
= 0,5b hb, значит, hb —= 5,625 (см). 3,2 472. Ж = 0,5а • Ь; а = 7х; Ь = 12x, Ь = 24 см. № 475. У каз а н и е : нужно разделить отрезок ВС на три равные части ВК, КЕ, ЕС, используя теорему Фалеса. в Рис. |
|
IV этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
— Какие формулы повторили на уроке? — Как найти площадь треугольника? Площадь прямоугольного треугольника? — Составьте синквейн к уроку |
(И) Домашнее задание: решить задачи № 468 (в, г), 473, 469 |
|
|
Цель деятельности чителя |
Создать условия для доказательства теоремы об отношении площадей треугольников, имеющих по равному углу |
|||
|
Те мины и понятия |
Площадь т е гольника, авновеликие |
иг ы, отношение площадей |
||
|
Плани емые ез льтаты |
||||
|
П едметные мения |
Универсальные учебные действия |
|||
|
Владеют базовым понятийным аппаратом; умеют работать с геометрическим текстом |
Познавательные: умеют устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение. Регулятивные: умеют адекватно оценивать правильность или ошибочность выполнения учебной задачи. Коммуникативные: умеют находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, ешений, ассуждений |
|||
|
О ганизация п ост анства |
||||
|
Фо мы аботы |
Ф онтальная (Ф); индивидуальная (И) |
|||
|
Образовательные ес сы |
• Учебник. • Задания для индивидуальной и онтальной работы |
|||
|
этап. П ове ка домашнего задания. Тео етический оп ос |
||||
|
Цель деятельности |
Деятельность чителя |
Деятельность учащихся |
||
|
|
2 |
З |
||
|
Проверить уровень усвоения формул для нахождения площади треугольника |
— Сформулируйте и докажите теорему о площади треугольника. — Выведите формулу для вычисления площади прямоугольного треугольника. — Докажите, что если высоты двух треугольников равны, то их площади соотносятся как основания. (И) — Решите
задачи с последующей самопроверкой. Найти: SABC. Рис. |
Ответ: 36 см2 |
||
Продолжение
|
|
2 |
|
|
|
|
|
ABCD — квадрат, АВ Найти: SAB(X.
Найти: ЯСА. |
4 см Рис. 2
|
Рис. З |
Ответ: 15 см Ответ: 60 см 2 |
|
П этап. Мотивация к деятельности |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Через решение задач подготовить учащихся к восприятию новой теоремы |
1.СМ— медиана МВС, СК — медиана МСМ. НаЙТИ.• : SA(M : SACk : SB(k. 1 2 1 Ответ: — Рис. 4 М— середина АД К — середина CD. ABCD — выпуклый четырехугольник. Доказать: SMBkD АВС/) • Доказательство:
SADB : SMDB ,4BCl) : SMDkB
|
|||
|
III этап. Из чение новой темы |
||||
|
ель деятельности |
Совместная деятельность |
|||
|
Доказать теорему об отношении площадей треугольников, имеющих по равному гл |
(Ф) Теорема. Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведение сторон, заключающих равные углы. (Доказывает сам учитель.) |
|||
Продолжение
|
IV этап. Зак епление из ченного мате иала |
||
|
Цель деятельности |
Деятельность чителя |
Деятельность чащихся |
|
На примерах отработать применение данной теоремы |
(Ф) 1.
Дано:
к 2. Дано: Т = 8 см, ов=6 см, ОС = 5 см, 0D = 2 см, 2
Рис. 8 (И) Решить самостоятельно задачу. Площадь одного равностороннего треугольника в З раза больше, чем площадь другого равностороннего треугольника. Найдите сторону второго треугольника, если сторона первого равна 1. Решить самостоятельно задачу № 479 (б) |
1. Решение: : (АС • АВ) : (КМ • КМ = 15 : 14 2. Решение:
25 - 200 : 48 - (см2) 6 Про верка:
479 6 . 2,4 см |
|
Самостоятельная абота об чающего ха акте а |
||
|
Цель деятельности |
Задания для самостоятельной аботы |
|
|
|
2 |
|
|
Проверить уровень понимания доказанной теоремы |
Вариант 1 I . Две стороны треугольника равны 1 2 см и 9 см, а угол между ними 30 0 . Найдите площадь треугольника.
в Рис. 9 |
|
|
Цель деятельности УЧ ител я |
Создать условия для доказательства теоремы о площади трапеции |
|
|
Термины и понятия |
Площадь треугольника, площадь трапеции |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Владеют базовым понятийным аппаратом; умеют работать с геометрическим текстом |
Познавательные: умеют принимать решение в условиях неполной и избыточной, точной и вероятностной информации. Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: имеют целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И); групповая (Г) |
|
|
Образовательные ресурсы |
• Учебник. • Задания для индивидуальной работы |
|
Окончание
|
|
2 |
|
|
|
Вариант П 1. Найдите площадь треугольника, две стороны которого равны 6 см и 8 см, а угол между ними 30 0 .
Найти: в с Рис. 10 |
|
|
V этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) — Продолжите фразы: • Сегодня на уроке я узнал... • Мне было труднее всего... • Самым полезным для меня было... |
(И) Домашнее задание: решить задачи № 479 (а), 476 (а), 477 |
|
У рок 20. Тема: ПЛОЩАДЬ ТРАПЕЦИИ
Продолжение
|
этап. Прове ка домашнего задания. Теоретический опрос |
|
|
Цель деятельности |
Совместная деятельность |
|
Проверить уровень усвоения теоретических знаний; выявить трудности, возникшие при выполнении домашнего задания |
Провести блицопрос по теории. К доске вызывается учащийся для решения домашнего номера № 476 (а). Остальные ученики задают вопросы, возникшие У них. Задача № 476 (а).
Диагонали ромба разбивают его на четыре равных прямоугольных треугольника площади этих треугольников равны. SABCD = 4 • SАОВ • — АО • ОВ. 2 Так как диагонали ромба точкой пересечения делятся пополам, то АО = —АС, ОВ = — BD 1 значит, SABCD 4 —АС • —BD= —АС • ВД то есть площадь ромба равна половине произведения его диагоналей. 2 2 а) dl = 3,2 дм, 4 = 14 см = —4 ф =14 = 224 (см 2 ).
2 Ответ: 224 см |
|
Решение задачи с целью подготовки учащихся к восп иятию нового мате иала |
|
|
Цель деятельности |
Задания для самостоятельной работы |
|
Посредством реше- ния задачи подготовить учащихся к восприятию новой темы |
(И/Ф) Задача решается самостоятельно с последующим коллективным обсуждением решения. Найдите площадь трапеции ABCD, если основания AD и ВС равны соответственно 12 см и 8 см, боковая сторона АВ равна 6 см, ZA= 30 0 . Решение:
= О ВК : 2; = ВС • DH: 2. ABCD BkDH— прямоугольник, поэтому ВК = DH, тогда SABCD=вк• + ВО : 2. Рис. 2 АВ Найдем ВК из прямоугольного треугольника АВК, в котором ZA = 300 , АВ=6 см; вк- = З см. 2 ABCD-3 Ответ: SABCD= 27 см2 |
Продолжение
|
этап. Изучение нового материала |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Доказать формулу для вычисления площади трапеции |
(Ф/Г) 1. Понятие высоты трапеции. ОпреДеление. Перпендикуляр, проведенный из любой точки одного из оснований к прямой, содержащей другое основание, называют высотой трапеции. ВН, Щ - высоты трапеции АВСД вн= DHl. 2. Решение задачи. Найти площадь трапеции ABCD, если основания AD и ВС равны а и Ь соответственно, а высота — Н. Задачу можно предложить решить самостоятельно или в небольших группах, затем обсудить решение, записать на доске и в тетрадях в виде теоремы с доказательством. Теорема. Площадь трапеции равна произведению полусуммы ее оснований на высоту. (Теорема Доказывается учителем вместе с учениками; можно преДложшпь учащимся самостоятельно разобрать ее по учебнику.) |
||
|
этап. Решение задач на закрепление изученной формулы |
|||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
|
|
2 |
З |
|
|
На примерах простых задач отработать применение доказанной формулы |
1 . Решить задачу. Дана трапеция, в которой основания равны 2 и 7, а площадь 18. Найти высоту. 2. Решить № 480, 481, 482 (самостоя тельно в парах, с последующей проверкой) |
От вет : высота равна 4. .N2 480.
6) Если ZD = 30 0 , ВС = 2 см, О = 10 см, DC = 8 см, то S-? 1 В ADCCI ZC: = 90 0 , О = 300 , значит, СС = —CD = 4 см, 2 но, 4 см. — (2 + 10) 4= 24 СМ 2 2 |
Рис. 4 ВЗ см. следователь- |
Окончание
|
|
|
|
2 |
|
|
|
|
|
|
|
|
ТО SABCD= 72 см2 . 2 481. D Рис. 5 дано: ABCD -трапеция. ZD = 90 0 , ВС = 0=6, 135 0 . Найти: SABCD.
1) ВД LAD, рассмотрим МВД: ZB1 = 900 , ZA = ZB = 45 0 , значит, АД = ВД = 6 см, отсюда О = + ВР =6+6= 12 см. 2) SABCD. = — (AD+BC) • СО S : щ (12+6) • 54 см 2 = 2 2 2 Ответ: 54 см
дано: ABCD -трапеция. АВ = СД = 135 0 Найти: SABCD• Решение: Рис. 7 1) Рассмотрим МВД: ZBl 900 , ZA = ZB = 45 0 , следовательно, Щ = Щ = см; аналогично из АССР: СР = Щ = 1 ,4 см. 2) = вр- ср ВС, = 3,4 — 1,4 = 2 см, значит, ВС = 2 см. AD=ABl + ВР- + = см. 1 2 З) SABCD= — (О + ВС) • Щ; , = — (4,8 + 2) • = 4,76 см 2 2 2 Ответ: 4,76 см |
|
|
|
|
IV этап. Итоги урока. Рефлексия |
||
|
|
Деятельность учителя |
|
|
Деятельность учащихся |
|
|
— Составьте синквейн к |
ок |
|
|
(И) Домашнее задание: S 2, вопрос 7, с. 133; № 518 |
|
У рок 21. Тема: РЕШЕНИЕ ЗАДАЧ НА ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ФИГУР
|
Цель деятельности чителя |
Создать условия для ознакомления учащихся с методами решения задач по теме «Площадь многоугольников» |
|||||||||||
|
Те мины и понятия |
Площадь т е гольника, площадь т апеции, площадь п ямо гольника и па аллелог амма |
|||||||||||
|
Плани емые ез льтаты |
||||||||||||
|
П едметные мения |
Униве сальные чебные действия |
|||||||||||
|
Владеют базовым понятийным аппаратом; умеют работать с геометрическим текстом |
Познавательные: умеют принимать решение в условиях неполной и избыточной, точной и вероятностной информации, выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки. Регулятивные: принимают и сохраняют цели и задачи учебной деятельности. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: имеют целостное мировоззрение, соответствующее современному уровню вВИТИЯ на ки и общественной п актики |
|||||||||||
|
О ганизация п ост анства |
||||||||||||
|
Фо мы аботы |
Ф онтальная Ф ; индивид альная И ; г пповая Г |
|||||||||||
|
Образовательные ес сы |
• Учебник. • Задания для индивид альной и г пповой аботы |
|||||||||||
|
этап. П ове ка домашнего задания |
||||||||||||
|
ель деятельности |
Задания для самостоятельной аботы |
|||||||||||
|
Проверить уровень сформ ированности теоретических знании по данной теме |
(И) Тест (см. Ресурсный материал) |
|||||||||||
|
П этап. Решение задач |
||||||||||||
|
ель деятельности |
Задания для самостоятельной аботы |
|||||||||||
|
Научить решать задачи на применение формул площадей |
(Г) 1. В трапеции АВСМ одно из оснований в З раза меньше другого, а высота составляет 75 % большего основания. Площадь трапеции равна 72 см-. Найдите основания и высоту трапеции. 2. В параллелограмме ABCD на стороне AD отмечена точка М так, что АМ : ЛО = 3 : 2. Найдите площадь ЛАВМ, если площадь параллелограмма равна 60 см 2. З. В параллелограмме КМРТ диагональ МТ перпендикулярна стороне МК, КМ = 13 см, МТ = 5 см. Найдите площадь параллелограмма и его высбты, если МР = 14 см. 4. В ДКМР высота МВ делит сторону КР на отрезки 6 см и 8 см, ZMkP = 45 0 . Найдите площадь ЛКМР.
|
|||||||||||
Окончание табл.
|
III этап. Итоги урока. Рефлексия |
|
|
Деятельность учителя |
Деятельность учащихся |
|
— Сформулируйте теорему о нахождении площади прямоугольника. — Сформулируйте теорему о нахождении площади параллелограмма. — Сформулируйте теорему о нахождении площади треугольника. — Сформулируйте теорему о нахождении площади трапеции. — Оцените свою работу |
(И) Домашнее задание: выполнить задания на карточках (см. Ресурсный материал) |
Тест
Вариант 1 ![]() . Выберите верные
утверждения:
. Выберите верные
утверждения:
а) площадь прямоугольника равна произведению двух его сторон;
б) площадь квадрата равна квадрату его стороны;
в) площадь прямоугольника равна удвоенному произведению двух его соседних сторон.
![]() 2. Закончите фразу: площадь ромба равна половине
произведения...
2. Закончите фразу: площадь ромба равна половине
произведения...
а) его сторон;
б) его стороны и высоты, проведенной к этой стороне;
в) его диагоналей.
З. По формуле S = а • ha можно вычислить площадь:
а) параллелограмма;
б) треугольника;
в) прямоугольника.
4. Площадь трапеции ABCD с основаниями АВ и CD и высотой ВН вычисляется по формуле:
а) ![]() ВН•,
ВН•,
![]()
в) (АВ+ СД : 2 • вН.
5. Выберите верное утверждение.
Площадь прямоугольного треугольника равна:
а) половине произведения его стороны на какую-либо высоту;
б) половине произведения его катетов;
в) произведению его стороны на проведенную к ней высоту.
6. В треугольниках АВС и №INk ZB = ZN. Отношение площадей треугольников АВС и №fNk равнс
![]()
![]() АВ • ВСВС • АС а)б)в) пл • мк ЛК • МК
АВ • ВСВС • АС а)б)в) пл • мк ЛК • МК
7.
В треугольниках MNk и DOS высоты ЛЕ и ОТ равны. Тогда SMNk . l)OS![]()
![]() 6)
МК : ps•, в) ЛК : os.
6)
МК : ps•, в) ЛК : os.
Вариант II 1. Выберите верные утверждения:
а) площадь квадрата равна произведению его сторон;
б) площадь прямоугольника равна произведению его противолежащих сторон;
в) площадь прямоугольника равна произведению двух его соседних сторон.
2. Закончите фразу: площадь параллелограмма равна произведению...
а) двух его соседних сторон;
б) его стороны на высоту, проведенную к этой стороне;
в) двух его сторон.
З. По формуле S = d, • : 2 можно вычислить площадь:
а) параллелограмма;
б) треугольника;
в) ромба.
![]() 4.
Площадь трапеции ABCD с основаниями ВС и AD и высотой СН вычисляется по
формуле:
4.
Площадь трапеции ABCD с основаниями ВС и AD и высотой СН вычисляется по
формуле:
а) S= СН • (ВС + О) : 2;
![]()
5. Выберите верное утверждение. Площадь треугольника равна:
а) половине произведения его сторон;
б) половине произведения двух его сторон;
в) произведению его стороны на какую-либо высоту.
6.
В треугольниках АВС и DEF ZC= ZF. Отношение площадей треугольников АВС и
DEF равно..![]()
АС • АВ АВ•АС АС • ВС а) 6) в)
DE•DF DE•EF DF•EF
7.
В треугольниках DEF и TRQ высоты Т и ТВ равны. Тогда SDEF:![]()
![]()
|
Ответы к тес |
|
2 |
З |
4 |
5 |
6 |
7 |
|
Ва иант |
б |
в |
а |
в |
б |
а |
б |
|
Ва иант П |
в |
6 |
в |
а |
6 |
в |
а |
Карточки для домашнего задания
1.
Одно из оснований трапеции на 3 см больше высоты, а другое на 3
см меньше высоты. Найдите основания и высоту трапеции, если ее площадь равна
100 см2![]()
2. В равнобедренной трапеции тупой угол равен 135 0 , а высота в 3 раза меньше большего основания. Найдите площадь трапеции, если меньшее основание равно 6 см.
У р о к 22. Тема: РЕШЕНИЕ ЗАДАЧ НА ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ФИГУР
|
Цель деятельности учителя |
Создать условия для закрепления знаний учащихся по теме «Площадь многоугольников» |
|
|
Термины и понятия |
Площадь треугольника, площадь трапеции, площадь прямоугольника и параллелограмма |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Владеют базовым понятийным аппаратом; умеют работать с геометрическим текстом |
Познавательные: умеют принимать решение в условиях неполной и избыточной, точной и вероятностной информации, выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки. Регулятивные: принимают и сохраняют цели и задачи учебной деятельности. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: имеют целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные ресурсы |
• Учебник. • Задания для индивидуальной работы |
|
|
1 этап. Актуализация опорных знаний |
||
|
Цель деятельности |
Совместная деятельность |
|
|
|
2 |
|
|
Отработать навыки решения задач на готовых чертежах |
(ФИ) 1. Решить задачи (устно).
6 А Рис. Рис. 2 |
|
Продолжение
|
|
|
2 |
||
|
|
3) Найти SABC, если треугольник — прямоугольный. в
4 Рис. 4) Найти SABC. В
Рис. 4 ответы : 1) 4,8; 2) 2. Решить задачи с последующей самопроверкой (письменно). 1) Найти ,soc. в 2) Дан равнобедренный треугольник АВС с основанием АС этого треугольника. 3) АВМ- трапеция, ВС : З; вк=б , SABCD= 60. Найти: ВС, О. ответы: 1) 27; 2) 36; 3) 8 и 12 |
5) АС: 12 , SABCD= 48. Найти: BD. В
6) Найти SABCD.
= 8; 6) SABCD —- 37,5. и углом при основании 75
|
Рис. 5
Рис. 6 0 , боковая сторона 12. Найти площадь 8 |
|
|
ll этап. Самостоятельная абота |
|
|||
|
Цель деятельности |
Задания для самостоятельной аботы |
|||
|
|
2 |
|||
|
Выявить уровень самостоятельности при решении задач |
Вариант 1 1. Сторона параллелограмма равна 21 см, а высота, проведенная к ней, 15 см. Найдите площадь параллелограмма. 2. Сто она т е гольника авна 5 см, а высота, проведенная к ней, в 2 аза больше сто оны. Найдите площадь т е гольника. |
|||
Окончание
|
|
2 |
|
|
|
З. В трапеции основания равны 6 и 10 см, а высота равна полусумме длин оснований. Найдите площадь трапеции. 4. Стороны параллелограмма равны 6 и 8 см, а угол между ними равен 300 . Найдите площадь параллелограмма. 5. Диагонали ромба относятся как 2 : З, а их сумма равна 25 см. Найдите площадь ромба. Вариант П 1. Сторона параллелограмма равна 17 см, а его площадь 1 87 см 2 . Найдите высоту, проведенную к данной стороне. 2. Сторона треугольника равна 18 см, а высота, проведенная к ней, в З раза меньше стороны. Найдите площадь треугольника. З. В трапеции основания равны 4 и 12 см, а высота равна полусумме длин оснований. Найдите площадь трапеции. 4. Стороны параллелограмма равны 4 и 7 см, а угол между ними равен 150 0 . Найдите площадь параллелограмма. 5. Диагонали омба относятся как З : 5, а их с мма авна 8 см. Найдите площадь омба |
|
|
III этап. Итоги ока. Ре лексия |
||
|
Деятельность чителя |
Деятельность ЧаЩИХСЯ |
|
|
— Какие формулы повторили на уроке? Какой этап урока оказался для вас наиболее сложным? Оцените свою або на оке |
Домашнее задание: выполнить другой вариант самостоятельной работы |
|
У рок 23. Тема: ТЕОРЕМА ПИФАГОРА
|
Цель деятельности чителя |
Создать условия для выведения доказательства теоремы Пифагора и ее применения при решении задач |
|
|
Те мины и понятия |
П ямо гольныйт е гольник, катеты, гипотен за |
|
|
Плани емые ез льтаты |
||
|
П едметные мения |
Униве сальные чебные действия |
|
|
Владеют геометрическим языком, умеют использовать его для описания предметов окружающего мира |
Познавательные: умеют видеть математическую задачу в контексте проблемной ситуации в окружающей жизни. Регулятивные: понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: имеют целостное мировоззрение, соотвтествующее современному уровню азвития на ки и общественной п актики |
|
|
О ганизация п ост анства |
||
|
Фо мы аботы |
Ф онтальная Ф); индивид альная (И |
|
|
Образовательные ресурсы |
• Учебник. • Задания для фронтальной работы. • Исто ические сведения о тео еме Пи аго а |
|
Продолжение
|
|
этап. Ак ализация опо ных знаний |
||||
|
|
Анализ самостоятельной аботы |
||||
|
|
Решение задач по готовым че тежам |
||||
|
цель деятельности |
Совместная деятельность |
||||
|
Подготовить учащихся к восприятию новой темы |
м к Рис. 2 |
||||
|
|
П этап. Из чение нового мате иала |
||||
|
ель деятельности |
Совместная деятельность |
||||
|
Показать историческую значимость тео емы Пи аго а |
(Ф) Историческая справка (см. Ресурсный материал) |
||||
|
|
оказательство тео емы |
||||
|
ель деятельности |
Совместная деятельность |
||||
|
Предложить учащимся доказательство, отличное от представленного в учебнике |
(Ф) Теорема. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
|
||||
|
|
5 |
|
|||
|
|
|
в Рис. З |
|||
|
|
III этап. Зак епление из ченного мате иала |
||||
|
ель деятельности |
Деятельность чителя |
еятельность чащихся |
|||
|
|
2 |
З |
|||
|
На примере решения простейших задач отработать формулу данной тео емы |
(Ф/И) 1. Решить № 483 (а, б), 484 (а, б) (устно). 2. На доске и в тетрадях решить № 487. 3. Самостоятельно решить № 485, 486 |
ЛЬ 483 (а, б). 62 + 8 2 = 100, значит, гипотенуза равна 10. 5 2 + 62 = 61, значит, гипотенуза равна 4.46 |
|||
Продолжение
|
|
2 |
|
|
|
|
N2 487. в Дано: ЛАВС — равнобедренный,
BD — высота. Найти: ВД
Решение. 1) В равнобедренном треугольнике высота, проведенная к основанию, является медианой, поэтому AD = АС 2
2) ДАТ) — прямоугольный. По теореме Пифагора: АВ2 = АО + В», откуда В» = АВ2 -AD2= 17 2 -8 2 = 225. Так как BD > 0, то 15 см.
дано: МВС, ZC = 90 0 И = 600 , с. Найти: ВС. С Рис. 5 Решение. 1) Так как = 30 0 , то АС = З 2) ВС2 = - АСИ, ВС2 = 8 8 = —с , следовательно, ВС =
а)
Если АВ = 5, АС = 13, то О— ? 02 = АС2 - 12. Рис. 6 6) Если 1,5, АС = 2,5, то ВС — ? ВС2 = АС2 -АВ2 •, ВС 2 — - 6,25 — 2,25 = 4, следовательно, ВС = 2. в) Если BD = 17, ВС = 15, то CD—? с» = в» - вс2 , с» — - 289 — 225 = 64, следовательно, CD = 8 |
Окончание
|
|
1V этап. Итоги урока. Рефлексия |
|
|
Деятельность учителя |
|
Деятельность учащихся |
|
— С какой теоремой познакомились на уроке? — Составьте синквейн к ок |
|
(И) Домашнее задание: подготовить сообщение о жизни Пифагора и его школе |
Историческая справка
![]() Установлено, что
теорема Пифагора встречается в вавилонских текстах, написанных за 1200 лет до
Пифагора. В математической книге Древнего Китая Чу-пей так говорится о
пифагоровом треугольнике со сторонами 3, 4 и 5: «Если прямой угол разложить на
составные части, то линия, соединяющая концы его сторон, будет 5, когда
основание есть 3, а высота 4». Кантор (крупнейший немецкий историк математики)
считает, что равенство 3 2 + 42 = 5 2 было
известно уже египтянам еще около 2 300 г. до н. э., во времена царя Аменемхета
(согласно папирусу 6 61 9, хранящемуся в Берлинском музее). Несколько больше
известно о теореме Пифагора у вавилонян. В одном тексте, относимом ко времени
Хаммураби, то есть к 2 000 г. до н. э., приводится приближенное вычисление
Типотенузы прямоугольного треугольника. Отсюда можно сделать вывод, что в
Двуречье умели производить вычисления с прямоугольными треугольниками, по
крайней мере в некоторых случаях. У индусов, как и у египтян и вавилонян,
геометрия была тесно связана с культом. Весьма вероятно, что теорема о квадрате
гипотенузы была известна в Индии уже около XVlll века до н. э-
Установлено, что
теорема Пифагора встречается в вавилонских текстах, написанных за 1200 лет до
Пифагора. В математической книге Древнего Китая Чу-пей так говорится о
пифагоровом треугольнике со сторонами 3, 4 и 5: «Если прямой угол разложить на
составные части, то линия, соединяющая концы его сторон, будет 5, когда
основание есть 3, а высота 4». Кантор (крупнейший немецкий историк математики)
считает, что равенство 3 2 + 42 = 5 2 было
известно уже египтянам еще около 2 300 г. до н. э., во времена царя Аменемхета
(согласно папирусу 6 61 9, хранящемуся в Берлинском музее). Несколько больше
известно о теореме Пифагора у вавилонян. В одном тексте, относимом ко времени
Хаммураби, то есть к 2 000 г. до н. э., приводится приближенное вычисление
Типотенузы прямоугольного треугольника. Отсюда можно сделать вывод, что в
Двуречье умели производить вычисления с прямоугольными треугольниками, по
крайней мере в некоторых случаях. У индусов, как и у египтян и вавилонян,
геометрия была тесно связана с культом. Весьма вероятно, что теорема о квадрате
гипотенузы была известна в Индии уже около XVlll века до н. э-
Основываясь, с одной стороны, на сегодняшнем уровне знаний о египетской и вавилонской математике, а с другой, на критическом изучении греческих источников, голландский математик Ван-дер-Варден сделал следующий вывод: «Заслугой первых греческих математиков, таких как Фалес, Пифагор и пифагорейцы, является не открытие математики, но ее систематизация и обоснование. В их руках вычислительные рецепты, основанные на смутных представлениях, превратились в точную науку».
У р о 24. Тема: ТЕОРЕМА, ОБРАТНАЯ ТЕОРЕМЕ ПИФАГОРА
|
Цель деятельности чителя |
Создать условия для выведения доказательства теоремы, обратной теореме Пифагора, и ее применения при решении задач |
|
|
Те мины и понятия |
П ямо гольныйт е гольник, катеты, гипотен за |
|
|
Плани емые ез льтаты |
||
|
П едметные мения |
Униве сальные чебные действия |
|
|
Владеют геометрическим языком, умеют использовать его для описания предметов окружающего мира |
Познавательные: умеют видеть математическую задачу в контексте проблемной ситуации в окружающей жизни. Регулятивные: понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: имеют целостное мировоззрение, соответствующее современному уровню азвития на ки и общественной п актики |
|
Продолжение
|
|
Организация пространства |
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
Образовательные ресурсы |
• Учебник. • Исторические сведения о применении теоремы Пифагора |
|
|
этап. Актуализация опорных знаний |
|
|
Проверка домашнего задания |
|
Цель деятельности |
Совместная деятельность |
|
Проверить, какие сообщения подготовили учащиеся |
(И) Учащиеся выступают со своими сообщениями или презентациями. (Ф) Учитель рассказывает о применении теоремы Пифагора (см. Ресурсный материал) |
|
|
II этап. Мотивация к деятельности |
|
Цель деятельности |
Постановка учебной задачи |
|
Подвести учащихся к теореме, обратной теореме Пифагора |
(Ф) Сформулировать утверждения, обратные данным, и выяснить, верны ли они: • Сумма смежных углов равна 1800 . • Диагонали ромба взаимно перпендикулярны. • Вертикальные углы равны. • В параллелограмме противолежащие стороны равны. • В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. (В последнем случае учащиеся смогут сформулировать утверждение, обратное Данному, а провести Доказательство его справедливости может помочь учитель.) |
|
|
III этап. Изучение нового материала |
|
Цель деятельности |
Совместная деятельность |
|
Доказать теорему, обратную теореме Пифагора |
(Ф) 1 . Учитель доказывает данную теорему. 2. Прямоугольные треугольники, длины сторон которых выражаются целыми числами, называются пифагоровыми треугольниками. Например, треугольник со сторонами 26, 24 и 10. — Приведите примеры пифагоровых треугольников. (10, 8 и б; 13, 12 и 5; 5, 4 и З; 15, 12 и 9 и Другие.) 3. Являются ли пифагоровыми треугольники: а) с гипотенузой 25 и катетом 15; б) с катетами 5 и 4? 4. Треугольник со сторонами З, 4, 5 был известен еще древним египтянам. Египтяне использовали его для построения прямых углов. Делали они это так: на веревке делали метки, делящие ее на 12 равных частей, связывали концы веревки и растягивали на земле с помощью кольев в виде треугольника со сторонами З, 4 и 5. Угол, лежащий против стороны, равной 5, оказывался прямым. Этот треугольник получил название египетского треугольника и по сей день именно так его и называют |
Окончание
|
IV этап. Закрепление изученного материала |
|||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
|
Закрепить изученные теоремы при решении простейших задач |
(ФМ) 1. Решить № 498 (а, 6, в) (устно). 2. Решить задачу № 499 (а). Один из учащихся по указанию учителя выходит к доске, остальные работают в тетрадях. З. Решить самостоятельно задачи: а) Определите углы треугольника со сторонами 1, 1, . (45 0, 45 0, 90 0.) б) В треугольнике АВС АВ = , ВС = 2. На стороне АС отмечена точка М так, что АМ= 1, 1. Найдите АС. (1 + Ф.) в) В треугольнике МРК РК = 2. На стороне МК отмечена точка А так, что МА = АР = , АК = 1. Найдите ДИРК. (75 0.) |
499 (а). 25 2 = 242 + 7-, значит, треугольник прямоугольный и его площадь равна половине произведения его катетов, то есть
Меньшая высота проведена к
большей стороне, а в прямоугольном треугольнике большей стороной является
гипотенуза, значит, S = hc • с : 2, где с — гипотенуза, hc — высота,
проведенная к гипотенузе, тогда hc.
Ответ: 6,72 см |
|
|
kV этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
(И/Ф) Учащиеся продолжают фразы: • Теперь я узнал, что.. • Теперь я могу... • Раньше я не понимал, как... • Раньше я не знал, что. • Теперь я знаю, что |
(И) Домашнее задание: п. 56; вопросы 9, 1 0; решить задачи № 498 (г, д, е), № 499 (6), 488 |
||
Применение теоремы Пифагора В архитектуре.
В зданиях готического и романского стиля верхние части окон расчленяются каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон.
Способ построения окна в готическом стиле очень прост. Легко найти центры шести дуг окружностей, радиусы которых равны ширине окна (Ь) для
наружных дуг и половине ширины для внутренних дуг. Остается еще полная окружность, касающаяся четырех дуг. Так как она заключена между 2
двумя концентрическими окружностями, то ее диаметр равен
расстоянию между этими окружностями, то есть — и, следовательно, радиус равен —![]()
2 4 Тогда становится ясным и положение ее центра. В рассмотренном примере радиусы находились без всяких затруднений. В других аналогичных примерах могут потребоваться вычисления. Покажем, как применяется в таких задачах теорема Пифагора.
В романской архитектуре часто встречается мотив, представленный на рисунке. Если Ь по-прежнему обозначает шири-
Ь Ь
ну окна, то радиусы полуокружностей будут равны R ![]() Радиус
р внутренней окружности можно вычислить
Радиус
р внутренней окружности можно вычислить
2 4
![]() 2 из
прямоугольного треугольника, катет которого изображен на рисунке пунктиром.
Гипотенуза этого треугольника, прохо-
2 из
прямоугольного треугольника, катет которого изображен на рисунке пунктиром.
Гипотенуза этого треугольника, прохо-
а 2 22
![]() Ь дящая через точку
касания окружностей, равна — + р, один катет равен , а другой — — р. По теореме
Пифагора имеем
Ь дящая через точку
касания окружностей, равна — + р, один катет равен , а другой — — р. По теореме
Пифагора имеем![]()
4 2 4 4
Решив данное уравнение, легко найти радиус внутренней
окружности р![]()
6
В строительстве.
Возможно, кто-то сочтет приложения теоремы Пифагора сугубо
теоретическими. Но это не так. Если, например, рассматривать треугольную приз![]() му
как крышу башни, то в первом вопросе речь идет о том, какой длины нужно сделать
боковые ребра, чтобы при данной площади чердака была выдержана предписанная
высота крыши. Заметим, что расчет площади кровли можно сильно упростить, если
воспользоваться одним очень простым правилом, справедливым во всех случаях,
когда все скаты крыши, сколько бы их ни было, имеют одинаковый уклон. Оно
гласит: «Чтобы найти площадь поверхности двускатной крыши, все скаты которой
имеют равный уклон, нужно умножить площадь чердака ,.Sq на длину стропила и разделить
на половину ширины дома».
му
как крышу башни, то в первом вопросе речь идет о том, какой длины нужно сделать
боковые ребра, чтобы при данной площади чердака была выдержана предписанная
высота крыши. Заметим, что расчет площади кровли можно сильно упростить, если
воспользоваться одним очень простым правилом, справедливым во всех случаях,
когда все скаты крыши, сколько бы их ни было, имеют одинаковый уклон. Оно
гласит: «Чтобы найти площадь поверхности двускатной крыши, все скаты которой
имеют равный уклон, нужно умножить площадь чердака ,.Sq на длину стропила и разделить
на половину ширины дома».
![]()
![]() При
строительстве любого сооружения рассчитывают расстояния, центры тяжести,
размещение опор, балок и т. д. В целом значение теоремы, кроме вышесказанного,
в том, что она применяется практически во всех современных технологиях, а также
открывает простор для создания и придумывания новых.
При
строительстве любого сооружения рассчитывают расстояния, центры тяжести,
размещение опор, балок и т. д. В целом значение теоремы, кроме вышесказанного,
в том, что она применяется практически во всех современных технологиях, а также
открывает простор для создания и придумывания новых.
В физике.
Молниеотвод, громоотвод — устройство для защиты зданий, промышленных, транспортных, коммунальных, сельскохозяйственных и других сооружений от ударов молнии. Известно, что молниеотвод защищает от молнии все предметы, расстояние до которых от его основания не превышает его удвоенной высоты. Необходимо определить оптимальное положение молниеотвода на двускатной крыше, обеспечивающее наименьшую его доступную высоту.
По теореме Пифагора, h2 > а2 + b 2
, значит, h![]()
В астрономии.
В конце XIX века высказывались разные предположения о существовании обитателей Марса, подобных человеку. Это явилось следствием открытий итальянского астронома Скиапарелли (открыл на Марсе каналы, которые долгое время считались искусственными). Естественно, что вопрос о том, можно ли с помощью световых сигналов объясняться с этими гипотетическими существами, вызвал оживленную дискуссию. Парижской академией наук была даже установлена премия в 100 000 франков тому, кто первый установит связь с каким-нибудь обитателем другого небесного тела; эта премия все еще ждет счастливца. В шутку, хотя и не совсем безосновательно, было решено передать обитателям Марса световой сигнал в виде теоремы Пифагора. Неизвестно, как это сделать; но для всех очевидно, что математический факт, выражаемый теоремой Пифагора, имеет место всюду, и поэтому похожие на нас обитатели другого мира должны понять такой сигнал.
В литературе.
Многие, услышав имя Пифагор, вспоминают известную теорему, но мало кто знает, что этот знаменитый грек имел отношение не только к математике, но и к литературе.
Великий математик был еще и великим философом своего времени. Вот некоторые его высказывания:
• Делая великое, не обещай великого.
• Как ни коротки слова «да» и «нет», всё же они требуют самого серьезного размышления.
• Не делай ничего постыдного ни в присутствии других, ни втайне.
• Первым твоим законом должно быть уважение к самому себе.
• Не закрывай глаз, когда хочешь спать, не разобравши всех своих поступков за прошедший день.
• По торной дороге не ходи.
Теорема Пифагора издавна широко применялась в разных областях науки, техники и практической жизни. О ней писали в своих произведениях римский архитектор и инженер Витрувий, греческий писатель-моралист Плутарх, греческий ученый III в. Диоген Лаэрций, математик V в. Прокл и многие другие.
Легенда о том, что в честь своего открытия Пифагор принес в жертву быка или, как рассказывают другие, сто быков, послужила поводом для юмора в творчестве писателей и поэтов. Так, например, немецкий писатель-романист А. Шамиссо, который в начале XIX в. участвовал в кругосветном путешествии на русском корабле «Рюрик», написал следующие стихи:
|
Пребудет вечной истина, как скоро Ее познает слабый человек! И ныне теорема Пифагора Верна, как и в его далекий век. Обильно было жертвоприношенье Богам от Пифагора. Сто быков Он отдал на закланье и сожженье |
За света луч, пришедший с облаков. Поэтому всегда с тех самых пор, Чуть истина рождается на свет, Быки ревут, ее почуя, вслед. Они не в силах свету помешать. А могут лишь, закрыв глаза, дрожать От страха, что вселил в них Пифагор. |
Легенда о смерти Пифагора.
Сонную тишину ночного Метапонта прорезал ужасный крик. Послышалось падение на землю тяжелого тела, топот убегающих ног, и все смолкло. Когда ночной караул прибыл на место происшествия, в колеблющемся свете факелов все увидели распростертого на земле старца, и неподалеку от него — мальчика 12 лет с лицом, перекошенным от ужаса.
— Кто это? — спросил начальник караула у мальчика.
— Это Пифагор, — ответил тот.
— Кто такой Пифагор? Среди жителей города нет гражданина с таким именем.
— Мы недавно прибыли из Кротона. Мой господин должен был скрываться от врагов и выходил только ночью. Они выследили его и убили.
— Сколько их было?
— Я этого не успел заметить в темноте. Они отбросили меня в сторону и накинулись на него.
Начальник караула стал на колени и приложил руки к груди старца.
— Конец, — сказал начальник.
«Одному только разуму, как мудрому попечителю, должно вверять свою жизнь».
|
Цель деятельности учителя |
Создать условия для совершенствования навыков решения задач на применение теоремы Пифагора и теоремы, обратной теореме Пифагора |
|||
|
Термины и понятия |
Прямоугольный треугольник, катеты, гипотенуза |
|||
|
Планируемые результаты |
||||
|
Предметные умения |
Универсальные учебные действия |
|||
|
Умеют применять изученные понятия, методы для решения задач |
Познавательные: осуществляют логические действия; формулируют ответы на вопросы. Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных задач, адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: имеют целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики. |
|||
|
Организация пространства |
||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|||
|
Образовательные ресурсы |
• Учебник. • Задания для индивидуальной работы |
|||
|
этап. Актуализация опорных знаний |
||||
|
Цель деятельнбсти |
Задания для самостоятельной работы |
|||
|
Проверить уровень сформированности знаний по теме |
(Ф) 1. Теоретический опрос. — Сформулировать теорему Пифагора. — Сформулировать теорему, обратную теореме Пифагора. (И) 2. Самостоятельное решение задач по готовым чертежам. Решение с Мследующей проверкой и обсуждением (при необхоДииости) (количество предложенных задач можно изменить). I . ABCD — параллелограмм. 2. DEll АС.
Рис.Рис. 2 |
|||
Продолжение
|
|
2 |
|||||||||
|
|
З. ABCD — трапеция. Найти. 6. Найти.• DC•, АС АВ.
4.
Рис. 4 Рис. 7 5. АВО-квадрат. Найти: АО. 8. ABCD - параллелограмм. Найти: АД
Е D Рис. 5 Рис. 8
2 8.AD= |
|||||||||
|
П этап. Решение задач |
||||||||||
|
Цель деятельности |
Деятельность учителя |
|
|
|
Деятельность учащихся |
|||||
|
|
2 |
|
|
|
|
|||||
|
Рассмотреть способы и методы решения задач повышенной сложности |
(Ф) 1. Решить № 517, 496, 497, 489 на дос- ке и в тетрадях |
|
З С |
Рис. 9 |
Дано.•'МВС
Найти: АС. |
|||||
Продолжение табл.
|
|
2 |
3 |
|
|
|
Решение: 1) Примем ВС = О = х, следовательно, в ОВС: ВС2 = DC2 + DB2 .
х (0+(3-х) 2 ; х2 =3 +9-6х+х2 •, 12; х =2•, см. 2) В ДОС: АС2 = АО + D&•, = 4+3 = Т, Ji Ответ: б Дано: ABCD — четырехугольник АВ=5 см, ВС= В см,
АВ2 = 25, ВС2 = 169, следовательно, 169 — 25 = 144 = АС С» = 81, AD2 = 225, следовательно, 225 — 81 = 144 = АС, значит ЛАВС и ЛАСЕ) — прямоугольные с общей стороной АС = 12 см. ABCD АВЫ) ACD, АЖ D= — АВ •АС+ — AC. CD 2 2 ABCD 2 2 Ответ: 98 см2
Дано: ABCD — параллелограмм, BD±AD , РАВСЮ— 50 см, О-АВ= см. Найти: ВД Решение: 1) Примем АВ = х см, следовательно, AD = (х + 1) см. Так как РАВМ =
2 2) В МВД В» = АВ2 -02 ; В» = 132 — 12 2 ; BD2 = 25, следовательно, BD = 5. Ответ: 5 см. |
Окончание
|
1 |
2 |
3 |
|
|
|
|
Дано: АВС — равносторонний, Доказать:
SAB(' 4 Рис. п 2 Доказательство: 2 2 2 = АВ2 —АЦ2 ; ВЦ 2 а За 1) Рассмотрим ДАВВ1.• BB1
а) если а = 5, то SABC
б) если а = 1,2, то SABC 0,366; в) если а = , то SABC = 2 ф |
|
|
III этап. Самостоятельная абота |
|||
|
ель деятельности |
Задания для самостоятельной аботы |
||
|
Закрепить полученные знания |
(И) При наличии времени можно предложить проверочную работу, которая сдается учителю. Вариант 1 В прямоугольной трапеции основания равны 22 см и 6 см, ббльшая боковая сторона — 20 см. Найдите площадь трапеции. Вариант П В прямоугольной трапеции боковые стороны равны 7 см и 25 см, а меньшее основание равно 2 см. Найдите площадь трапеции. Ва р и а нт III (для более подготовленных учащихся) Диагональ АС прямоугольной трапеции ABCD перпендикулярна боковой стороне CD и составляет угол 60 0 с основанием О. Найдите площадь т апеции, если AD = 24 см |
||
|
IV этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
— Оцените свою работу на уроке. — Какой этап ока вам показался наиболее сложным? Почем |
(И) Домашнее задание: № 490, 491 ; рассмотреть самостоятельно решение № 524 (вывод формулы Герона) (по желанию) |
||
|
Цель деятельности учителя |
Создать условия для совершенствования навыков решения задач по теме «Площадь», для ознакомления учащихся с формулой Герона; показать применение формулы Герона в процессе решения задач |
|
|
Термины и понятия |
Прямоугольный треугольник, катеты, гипотенуза, формула Герона |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Умеют применять изученные понятия, методы для решения задач |
Познавательные: осуществляют логические действия; формулируют ответы на вопросы. Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных задач, адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: имеют целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные ресурсы |
• Учебник. • Задания для фронтальной и индивидуальной работы |
|
|
этап. Актуализация опорных знаний |
||
|
Проверка домашнего задания |
||
|
Цель деятельности |
Совместная деятельность |
|
|
|
2 |
|
|
Проверить правильность выполнения домашнего задания |
(Ф/И) По готовым чертежам на доске проверить решение задач № 490, 491 (а).
Рис. Решение: а) 12 см, ВД МС, Щ = 8 см.
2 2 |
|

|
II этап. Из чение нового мате иала |
|||
|
оказательство о м лы Ге она |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Доказать формулу |
(Ф) Учитель Доказывает формулу вместе с учащимися, которые Дома разобрались с этой теоремой. Докажите, что площадь S треугольника со сторонами а, Ь, с выражается |
||
|
П именение |
о м лы Ге она п и ешении задач |
||
|
ель деятельности |
Деятельность чителя |
|
Деятельность чащихся |
|
Показать применение формулы Герона при решении задач |
(Ф) Решить № 499 на доске и в тетради (если в классе не успевают выполнить № 499 (б), то предложить в качестве домашней работы)
|
а)дано: МВС, АВ = 24 см, ВС = 25 см, АС = 7 см Найти: меньшую высоту. Решение: Меньшей высотой является та высота, которая опущена на ббльшую сторону. 1) В МВД AD2 = - В», в МСО AD2 = АС2 - С», следовательно, АВ2 - ВО = = АС2 — СО; 242 — .х2 = 72 — (25 — х)2 , следовательно, 576 — х2 = 49 — 625 + 50х — х2 50х = 1 1 52; х = 23,04, следовательно BD = 23,04 см. 2)
02 = АВ2 - В»; 02 = 24 2 -
АВ = 17 см, 4 Решение: 1) В МСК НС2 = АС - дВсН: НС2 = ВС2 — ВК, следовательно АС2 — АН2=
- вс2 - вн2, 225 -х2 = 64 - (17 - х)2; 225 -х2= 64-289+ в— , 4 следовательно, АН = В— 17
6) не = 15 2 В—4 = 225- 225, следовательно, 17 17 289 нс = 17 17 |
|
Окончание
|
III этап. Итоги урока. Рефлексия |
|
|
Деятельность учителя |
Деятельность учащихся |
|
— С какой формулой познакомились на уроке? — Можно ли было ешить № 499, п именяя о м л Ге она? |
(И) Домашнее задание: решить № 499, используя формулу Герона |
У р к 27. тема: РЕШЕНИЕ ЗАДАЧ НА ПРИМЕНЕНИЕ ТЕОРЕМЫ ПИФАГОРА. ФОРМУЛА ГЕРОНА
|
Цель деятельности учителя |
Создать условия для совершенствования навыков решения задач по теме «Площадь», используя теорему Пифагора, формулу Ге она |
||
|
Те мины и понятия |
П ямо гольныйт е гольник, катеты, гипотен за, |
о м ла Ге она |
|
|
Плани емые ез льтаты |
|||
|
П едметные мения |
Униве сальные чебные действия |
||
|
Умеют применять изученные понятия, методы для решения задач |
Познавательные: осуществляют логические действия; формулируют ответы на вопросы. Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных задач, адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения. Коммуникативные: умеют разрешать конфликты на основе согласования позиций и учета интересов. Личностные: имеют целостное мировоззрение, соответствующее современному овню азвития на ки и общественной п актики |
||
|
О ганизация п ост анства |
|||
|
Фо мы аботы |
Ф онтальная Ф ; индивид альная И |
||
|
Образовательные ес сы |
• Учебник. • Задания для онтальной и индивид альной аботы |
||
|
этап. Ак ализация опо ных знаний |
|||
|
П ове ка домашнего задания |
|||
|
ель деятельности |
Совместная деятельность |
||
|
|
2 |
||
|
Проверить степень усвоения теоретического материала и умения его применять п и ешении задач |
(ф) 1 . Ответить на вопросы учащихся по выполнению домашнего задания. 2. Провести математический диктант: 1 ) Записать формулу для вычисления площади треугольника. 2 Записать о м л для вычисления площади п ямо гольного е гольника. |
||
|
|
2 |
||
|
|
3) Записать формулу для вычисления площади равностороннего треугольника. 4) Записать формулу для вычисления площади прямоугольника. 5) Записать формулу для вычисления площади параллелограмма. 6) Записать формулу для вычисления площади ромба. 7) Записать формулу для вычисления площади трапеции. 8 Записать о м л Ге она |
||
|
П этап. Решение задач |
|||
|
Цель деятельности |
Деятельность учителя |
|
Деятельность учащихся |
|
|
2 |
|
3 |
|
Закрепить умение применять формулы площадей многоугольников и теорему Пифагора при решении задач |
(Ф) 1. На доске и в тетрадях решить задачи № 504, 517. К доске вызываются два ученика, один из них решает самостоятельно задачу № 504, другой — № 517. На местах учащиеся решают обе задачи, а затем проверяют решение с доски, ищут ошибки в своем решении и в решении на доске, высказывают свое мнение о правильности решения задач. |
504. Решение:
Рис. 2 Ответ: 900 см 517. 1-й способ. АКИ) —
АВС реме Пифагора, так треугольника ,soc- • 5 • 12=30 2 2-й способ. По формуле Герона роны треугольника. Рис 2 |
с Проведем высоту параллелограмма СЕ. Так как ОК Ш AD и СЕ Ш АД О — середина АС, то по теореме
В ОСЕ = 400 СЕ = 20 см. S АЖ D ДАВС и MCD — прямоугольные по теореме, обратной теокак 5 2 + 12 2 = 13 2, 9 2 + 122 = 1 5 2 . Площадь прямоугольного ab вычисляется по формуле S = , где а и Ь — катеты треугольника. 2
2 Я = р(р — —
— с) , где р = 9+12+15 15 (СМ), РАСТ) 2
|
|
Цель деятельности учителя |
Создать условия для проверки знаний, умений и навыков учащихся по усвоению и применению изученного материала |
|
Термины и понятия |
Площади четырехугольников, теорема Пифагора |
Окончание
|
1 |
2 |
З |
|
|
2. Решить задачу № 525 самостоятельно |
АСИ) АВ(7) — SABC + SACD—-30 + 54 = 84 (см2). Ответ: 84 см2
По формуле Герона ,SABC Рис. 2 — Др — АВ)(р — АВ+АС+ВС 13+14+15 где р = = 21 (см) 2 2
SBCM= 84-39- = 30 (см ясм-— — ВС • МЕ 2
МЕ =— 4— (см). вс Ответ: 4—см 7 |
|
III этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
— Какие трудности возникли у вас при решении задач? — Оцените свою работу на уроке |
(И) Домашняя работа: решить № 503, 5 8, подготовиться к контрольной работе |
|
У рок 28. Тема: КОНТРОЛЬНАЯ РАБОТА 2
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Умеют демонстрировать знание основных понятий, применять полученные знания для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности |
Познавательные: проводят сравнение, сериацию и классификацию по заданным критериям. Регулятивные: вносят необходимые коррективы в действие после его завершения на основе его учета характера сделанных ошибок, осуществляют самоанализ и самоконтроль. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: осознают важность и необходимость знаний для человека |
|
|
О ганизация пространства |
||
|
Формы работы |
Индивидуальная (И) |
|
|
Образовательные ресурсы |
• Учебник. • Задания для индивидуальной аботы |
|
|
этап. Выполнение контрольной работы по вариантам |
||
|
Цель деятельности |
Задания для кон ольной работы |
|
|
|
2 |
|
|
Проверить знания, умения и навыки по изученному материалу |
Вариант 1 1. Сторона треугольника равна 5 см, а высота, проведенная к ней, в два раза больше стороны. Найдите площадь треугольника. 2. Катеты прямоугольного треугольника равны 6 и 8 см. Найдите гипотенузу и площадь треугольника. 3. Найдите площадь и периметр ромба, если его диагонали равны 8 и 10 см. 4* В прямоугольной трапеции АВСК ббльшая боковая сторона равна см, угол К равен 45 0 , а высота СНделит основание АК пополам. Найдите площадь трапеции. Вариант П 1. Сторона треугольника равна 12 см, а высота, проведенная к ней, в три раза меньше стороны. Найдите площадь треугольника. 2. Один из катетов прямоугольного треугольника равен 12 см, а гипотенуза 13 см. Найдите второй катет и площадь треугольника. 3. Диагонали ромба равны 10 и 12 см. Найдите его площадь и периметр. 4*. В прямоугольной трапеции ABCD ббльшая боковая сторона равна 8 см, угол А равен 60 0 , а высота ВН делит основание AD пополам. Найдите площадь трапеции. Решение заданий контрольной работы Вариант 1 1 . S= 0,5а • h;, а- 5 см, Ответ: 25 см2 2. По теореме Пифагора с Ответ: 10 см, 24 см . |
|
з. в
Рис. D с в
450 к
Рис. 2
1. 0,5а • h;, а = 12 см,
2. По теореме Пифагора а s=5 • : 2=30 (см 2 ). Ответ: 5 см, 30 см 2.
з.
Рис.
D в
8
600
D Рис. 4
2
МОВ — прямоугольный.
АВ2 + ВО = 4 2 + 5 2 = мп (см).
= (СМ). 40 (см2) От вет : РАВО = 446 см; SABCD = 40 см 2.
АКСН — прямоугольный, равнобедренный, тогда КН = СН.
по теореме Пифагора СК2 = КН2 + СН2 , = КН2 + КН2, КН- З см, сн= З см.
Так как СН делит АК пополам, то АН = 3 см, АК = 6 см. ABCH— прямоугольник, ВС = АН = З см.
АВСК • : 2 • (3 +6) = 13,5 (с“).
Ответ: • к= 13,5 см2
Вариант П 12 : З = 4 (см), S= • 12 24 (см 2).
2 - 12 2 = 25, СМ.
МОВ — прямоугольный.
= АС • ВТ 2= 10 • 12 : 60 (см 2)
Отв е т : РАВО = 4 46 см; SAB(D= 60 см 2.
ДАВН— прямоугольный, в нем И = 600 , тогда ИВН= 30 0 , АН = 0,5АВ = 4 см. По теореме Пифагора ВН2 = АВ2 — АМ2 = 82 — 42 = 48, ВН= 4$ см. Так как ВИЧ делит AD пополам, то 4 см, AD = 8 см. HBCD — прямоугольник, ВС = HD = 4 см. = о,5ВН• = • 46 • (4 + 8) =2Ф5 (см 2 ).
Ответ : SABCD= 243 см2
Окончание
|
|
ll этап. Итоги |
ока. Ре лексия |
|
Деятельность чителя |
|
еятельность чащихся |
|
|
|
(И Домашнее задание: повто ить свойства п опо ций |
ГЛАВА VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ
У р о к 29. Тема: ПРОПОРЦИОНАЛЬНЫЕ ОТРЕЗКИ. ОПРЕДЕЛЕНИЕ ПОДОБНЫХ ТРЕУГОЛЬНИКОВ
|
Цель деятельности ч ителя |
Создать условия для определения пропорциональных отрезков, рассмотрения свойства биссектрисы треугольника и применения этого свойства п и ешении задач |
||
|
Те мины и понятия |
П опо циональные от езки, биссект иса гла, отношение, п опо ции, сходственные сто оны, коэ |
ициент подобия |
|
|
Плани емые ез льтаты |
|||
|
П едметные мения |
Униве сальные чебные действия |
||
|
У меют демонстрировать знание основных понятий, применять полученные знания для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности |
Познавательные: осуществляют логические действия; формулируют ответы на вопросы. Регулятивные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения математических проблем, адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: проявляют способность к эмоциональному восприятию математатических объектов, задач, ешений, асс ждениЙ |
||
|
О ганизация п ост анства |
|||
|
Фо мы аботы |
Ф онтальйая Ф индивид альная (И |
||
|
Образовательные ес сы |
• УчебниК |
||
|
этап. Анализ конт ольной аботы |
|||
|
[ ель деятельности |
Совместная деятельность |
||
|
Выявить трудности, возникшие при решении задач в конт ольной аботе |
. Сообщение итогов контрольной работы. 2. Анализ ошибок, допущенных учащимися в ходе работы. 3. Решение на доске задач, вызвавших зат днения чащихся |
||
|
II этап. Мотивация к деятельности |
|||
|
Цель деятельности |
Постановка чебной задачи |
||
|
|
2 |
||
|
Подготовить учащихся к введению понятия пропорциональных от езков |
(Ф) — Что называют отношением двух чисел? Что показывает отношение? — Отношение АВ к CD равно 2 : 7. О чем это говорит? Найдите отношение CD к АВ. В МВСАВ : ВС : АС = Р „ = 45 дм. Найдите сто оны т е гольника АВС |
||
|
|
2 |
|||
|
|
— Что называют пропорцией? Верны ли пропорции 1,5 : 1,8 25 : 30; 18 : 3 = 5 : 30? — В пропорции а : Ь = с : d укажите крайние и средние члены. Сформулируйте основное свойство пропорции. — Переставив средние или крайние члены пропорции, составьте три верные пропорции: а) 12 : 0,2 = 30 : 0,5; б) АВ : MN=CD КР — Найдите неизвестный член пропорции. а) : 12,3 : 6; |
|||
|
III этап. Изучение нового материала |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Ввести понятие пропорциональных отрезков |
(Ф) 1. Ввести понятие отношения отрезков. Определение. Отношением отрезков АВ и CD называется отношение их длин, то есть АВ : CD. 2. Ввести понятие пропорциональных отрезков. ОпреДеление. Отрезки АВ и CD пропорциональны отрезкам АД и (Л Д, если АВ : АД = CD : ClDl. Например: Если АВ = 5 см, CD = 7 см, AlBl = 7,5 см, ClDl = 1 0,5 см, то АВ : AlBl = CD : СО, то есть отрезки АВ и CD пропорциональны отрезкам АIВ1 и С, Д. З. Ввести понятие подобных фигур (два круга, два квадрата, два мяча разных размеров, изображения на кинопленке и на экране, на фотопленке и на фотографии и т. д.). 4. Ввести понятие подобных треугольников: АВ ВС АС
Стороны АВ и А В, ВС и ВС], АС и АС] называют сходственными. Определение. Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого. 5. Решить устно № 533, 534 (а, б). 6. Разобрать решение задачи № 535 (свойство биссектрисы треугольника) |
|||
|
IV этап. Закрепление изученного материала |
||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
|
|
|
2 |
3 |
|
|
|
При решении простых задач отработать понятия пропорциональных отрезков и сходственных сторон |
(Ф/И) 1. Один из учащихся решает задачу № 536 (б) на доске, остальные в тетрадях. 2. Решить самостоятельно № 541. Затем один из учеников выходит к доске, показывает решение, остальные сверяют, задают вопросы, оценивают себя |
Г,Г2 536 (6). Решение. Так как ZC = ZBDC, то ДОС равнобедренный с основанием CD, 9 следовательно, ВС = BD =16. |
|
30 20. |
|
Цель деятельности учителя |
Создать условия для закрепления понятий пропорциональных отрезков и подобных треугольников; для совершенствования навыков решения задач на применение свойства биссектрисы треугольника и определения подобных треугольников; для рассмотрения теоремы об отношении площадей подобных треугольников и ее применения в процессе решения задач |
|
Термины и понятия |
Пропорциональные отрезки, отношение, пропорции, сходственные стороны, коэффициент подобия |
Окончание
|
|
2 |
З |
|
|
|
|
Так как BD — биссектриса МВС, то вс АВ
АВ 2 Ответ: 10— . З Л'2 541. Решение. В ЛАВС И =
106 0 , ZB = 34 0 ZC = 180 - 80 0 — 140 0 = 40 0 40 0 О
= = 1800 - 1460 = 34 0 . По определению подобных треугольников, два треугольника называют подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.
= 40 0 ; ВС АВ : ответ: ДАВС-ОЕЕ |
|
|
IV этап. Итоги ока, Ре лексия |
|||
|
Деятельность чителя |
еятельность чащихся |
||
|
— Какие новые понятия узнали? Какие отрезки называются пропорциональными? — Какие стороны треугольника называются сходственными? — Оцените по пятибалльной шкале, насколько вы поняли материал ока |
(И) Домашнее задание: п. 58, 59, вопросы 1, 2, 3; решить задачи № 536 (а), 538, 542 |
||
У р о к 30. Тема: ОТНОШЕНИЕ ПЛОЩАДЕЙ ПОДОБНЫХ ТРЕУГОЛЬНИКОВ
|
Плани емые ез льтаты |
|||
|
П едметные мения |
Униве сальные чебные действия |
||
|
Умеют демонстрировать знание основных понятий, применять полученные знания для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности |
Познавательные: осуществляют логические действия; формулируют ответы на вопросы. Регулятивные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения математических проблем, адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве, умеют работать в группе. Личностные: проявляют способность к эмоциональному восприятию математатических объектов, задач, ешений, асс ждений |
||
|
О ганизация п ост анства |
|||
|
Фо мы аботы |
Ф онтальная Ф ; индивид альная И ; г пповая Г |
||
|
Образовательные ес сы |
• Учебник. • Задания для индивид алычой, онтальной аботы |
||
|
этап. Активизация знаний чащихся |
|||
|
Цель деятельности |
еятельность чителя |
Деятельность чащихся |
|
|
|
2 |
|
|
|
Выявить трудности, возникшие при выполнении домашнего задания; подготовить учащихся к восприятико новой темы |
. К доске вызвать троих учащихся: один из них готовит доказательство теоремы, двое оформляют на доске задачи № 538 и № 542. 2. В это время остальные учащиеся отвечают на теоретические вопросы, а затем решают задачи на готовых чертежах. 1 ) Что называется отношением двух отрезков? 2) В каком случае говорят, что отрезки АВ и C'D пропорциональны отрезкам А В и С] Д? З) Дайте определение подобных треугольников. Задачи. в 2
Найти: SACl). |
ЛГ2 538.
BD АС АВ AC•BD АС • 13,5 4,5 = ЗАС Рис. Рос +АС+ВС= ЗАС 42-18 АС = = 6 (см) АВ=З • 18 (см). 4 Ответ: АС = 6 см, АВ= 18 см. .N2 542. КМ ЛТ kN М ВС ДКЛТ
• (см). |
|
Продолжение
|
|
2 |
З |
|
|
|
SABC • SMNk Найти: МАТ.
м З) Двое учащихся работают по инДивиДуальным карточкам. 1-й уро вен ь (карточка 1). 1. Треугольники kPF и ЕЛП подобны, причем КР : МЕ = = РЕ : kF : ЕТ, ZF= 30 0 , ZE = 49 0 . Найдите остальные углы этих треугольников. 2. Биссектриса BD делит сторону АС треугольника АВС на отрезки AD и CD, равные соответственно 7 см и 10,5 см. Найдите периметр треугольника АВС, если известно, что АВ=9 см. 2-й уро вен ь (карточка 2). 1.
Найти: ВС. Рис. 4 2. Периметр треугольника равен 70 см, две его стороны равны 24 и 32 см. Найдите отрезки, на которые
биссектриса треголышка делит его т етью сто |
Отв е т: КМ = 8,4 см, 10,5 см, 14,7 см |
|
|
П этап. Из чение новой темы |
|||
|
ель деятельности |
Совместная деятельность |
||
|
Доказать теорему об отношении площадей подобных т е гольников |
(Г) I . Распределить учащихся по творческим группам и предложить обсудить в группах задачу: «Треугольники АВС и AlBlCl подобны с коэффициентом подобия К. Найти отношение их площадей». 2. Засл шать ва ианты ешений, выб ать из п едложенных наиболее дачный и ешение записать в тет адях и на доске |
||
|
III этап. Зак епление из ченного |
мате мала |
|
|
|
Цель деятельности |
еятельность чителя |
|
еятельность чащихся |
|
|
2 |
|
3 |
|
Научиться применять доказанную теорему |
1. Решить письменно задачу № 545 на доске и в тетрадях (записать краткое решение). Один из учащихся самостоятельно |
Г•Г2 545. ЛАВС- |
К- |
Окончание
|
|
2 |
|
|
|
|
решает задачу на доске, остальные — в тетрадях. После завершения работы проверяется правильность решения. (Г) 2. Решить задачи № 547, 548 (обсудить принцип решения задач, варианты решений заслушать всем классом) |
SABC на 77 СМ- больше SА SAB(,— + 77
• (36 -25) = 25 • 77
= 25 • 175 (см ) 77 + 175 = 252 (см). Ответ: 175 см2 и 252 см2 .N2 547. Краткое решение:
ЛАВС MlBlCl ВС = К • ВС 1, АС = К • AlCl
.AlBl + + 548. Краткое решение: ЛАВС MIBlCl, Ответ: 5 : 2 |
|
|
Самостоятельная абота |
|||
|
ель деятельности |
Задания для самостоятельной аботы |
||
|
Закрепить полученные знания |
(И) Учащиеся выполняют самостоятельную работу на листочках и сдают на проверку учителю (если время на уроке осталось, можно выполнить самоп ове к см. Рес сный мате иал |
||
|
IV этап. Итоги ока. Ре лексия |
|||
|
еятельность чителя |
еятельность чащихся |
||
|
— Оцените свою работу на уроке. — На каком этапе урока у вас возникли наибольшие затруднения? |
(И) Домашнее задание: п. 60, вопрос 4; повторить п. 52; решить задачи № 544, 543, 546, 549; решить задачу (по желанию): В трапеции ABCD (AD llBC) АС — биссектриса И делит трапецию на два подобных треугольника АВС и ACD, АВ = 9 см, CD 12 см. Найдите пеимет т апеции |
||
Ресурсный материал
Самостоятельная работа
1 . АВ и АД, ВС и BlCl — сходственные стороны подобных треугольников АВС и ЛВС), ВС : = 2,5, АС = 4 см, О = 47 0 21'. найдите Щ, АС и отношение этих треугольников.
![]() 2. Площади двух
подобных треугольников равны 16 см и 25 см 2 . Одна из сторон
первого треугольника равна 2 см. Найдите в сходственную ей сторону другого
треугольника.
2. Площади двух
подобных треугольников равны 16 см и 25 см 2 . Одна из сторон
первого треугольника равна 2 см. Найдите в сходственную ей сторону другого
треугольника.
![]() дано: ДВЕС- МВС, 16 см, СЕ-
9 см,
дано: ДВЕС- МВС, 16 см, СЕ-
9 см,
ZBEC — тупой. Найти: ВС.
1 . Треугольники АВС и AIBlCl подобны. ВС и ВС, АС и АС] — сходственные стороны. Найдите ZCl, АВ и отношение площадей этих треугольников, если АС : AlCI = 4,4, АД = 5 см, ZC= 15 0 31'.
2. Две сходственные стороны подобных треугольников равны 2 см и 5 см.
Площадь первого треугольника 8 см2![]()
Найдите площадь второго треугольника.
![]() 3*. Дано: ЛАВС МЕС,
DE не параллелен АВ, AD = 3 см,
3*. Дано: ЛАВС МЕС,
DE не параллелен АВ, AD = 3 см, ![]() 5 см, ВС = 7 см. Найти: СЕ.
5 см, ВС = 7 см. Найти: СЕ.
с
У рок 31. Тема: ПЕРВЫЙ ПРИЗНАК ПОДОБИЯ ТРЕУГОЛЬНИКОВ
|
Цель деятельности чителя |
Создать условия для выведения доказательства первого признака подобия треугольников и формирования у учащихся навыков п именения этого п изнакап и ешении задач |
||
|
Те мины и понятия |
П опорциональные от езки, отношение, п опо ции, сходственные сто оны, коэ |
ициент подобия |
|
|
Плани емые ез льтаты |
|||
|
П едметные мения |
Униве сальные чебные действия |
||
|
Умеют демонстрировать знание основных понятий, применять полученные знания для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности |
Познавательные: осуществляют логические действия; формулируют ответы на вопросы. Регулятивные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения математических проблем, адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения, контролировать процесс и результат учебной математической деятельности. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве, умеют работать в группе. Личностные: п оявляют познавательный инте ес к из чению п едмета |
||
|
О ганизация п ост анства |
|||
|
Фо мы аботы |
Ф онтальная (Ф); индивид альная И |
||
|
Образовательные ес сы |
• Учебник. • Задания для индивидуальной аботы |
||
|
I этап. Активизация знаний чащихся |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Проверить правильность выполнения домашней аботы |
(Ф) Проверка домашнего задания: № 544, 543, 546, 549 (Дополнительную задачу проверить инДизиДуально) |
||
Продолжение
|
|
П этап. Мотивация к деятельности |
|
|
Цель деятельности |
Постановка учебной задачи |
|
|
Подготовить учащихся к восприятию новой темы |
(Ф/И) Решение задач с целью подготовки учащихся к восприятию нового материала. (Самостоятельное решение с последующим обсуждением.) Обсуждение решений можно организовать таким образом: один из учащихся выходит к доске и предлагает свое решение, остальные предлагают свое или соглашаются с предложенным решением.
Найти: а) ВИ, В2В4; 6) SАзвзс • Решение: По теореме Фалеса СВ] = BlB2 = В2Вз = ВзВ4 = З см, следовательно, В2В4 = 6 см. ДАзВзС
ДА4В4С, К = — Ответ: ВИ = 3 см, В2В4 = 6 см S = 18 см2 в
Решение: СВ.СА 3CWf•4CN 2 а) = 12 = З см Рис. 2 САЛ CM•CN CM•CN АВ.АС 2Ak4NC 8
6) В) SBkNM= 36-3 - 13,5 = 19,5 (см 2). Ответ: а) SCW= З СМ 2 •, 6) 13,5 СМ 2 •, В) — 19,5 см2 |
|
|
|
III этап. Изучение новой темы |
|
|
Цель деятельности |
Совместная деятельность |
|
|
Доказать первый признак подобия треугольников |
(ФИ) 1. Сформулировать первый признак подобия треугольников. 2. Доказать первый признак подобия треугольников и записать план доказательства на доске и в тетрадях |
|
|
|
IV этап. Закрепление изученного материала |
|
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
|
2 |
3 |
|
Научить применять доказанную теорему при решении задач |
(Ф/И) Решить задачи № 550, 551, 553, 561 (устно) |
№ 550. а) Рассмотрим МВС и ACDE. ZC — -ZE = а (по условию), И = ZD = 900 (по условию), следовательно, ЛАВС -- ОСЕ (по двум углам), следовательно, |

Окончание
|
|
2 |
З |
|
|
|
N2 553. а) да; б) да; в) да.
Следовательно, ЛАВС &41BlC1 по двум углам. Рис. 7 N2 561.
МУ = ЛК = МК Доказать: ЛАВС лОж Рис. 8 Доказательство: 1) ЛАВС — равносторонний, значит, ZA = ZB = ZC = 600 ДЛТК— равносторонний, значит, ZM= ZN= Zk = 600 . 2)
Так как |
|
V этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
— Для того чтобы записать пропорциональность сторон подобных треугольников, что необходимо? — Сформулируйте первый признак подобия треугольников. — Составьте синквейн к уроку |
(И) Домашнее задание: выучить признак подобия треугольников; решить № 555. Дополнительная задача: На продолжении сторон DC (за точку С) и ВА (за точку А) параллелограмма ABCD взяты соответственно точки К и Е. КЕ пересекает сторону ВС в точке М, а сторону AD— в точке Е. Докажите, что АЕ • МС = КС • AF |
|
|
Цель деятельности учителя |
Создать условия для формирования у учащихся навыков решения задач на применение первого признака подобия треугольников |
|
|
Термины и понятия |
Пропорциональные отрезки, отношение, пропорции, сходственные стороны, коэффициент подобия |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Умеют демонстрировать знание основных понятий, применять полученные знания для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности |
Познавательные: осуществляют логические действия; формулируют ответы на вопросы. Регулятивные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения математических проблем, адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения, контролировать процесс и результат учебной математической деятельности. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве; умеют работать в группе. Личностные: проявляют познавательный интерес к изучению предмета |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные ресурсы |
• Учебник. • Задания для фронтальной, индивидуальной работы |
|
|
этап. Актуализация опорных знаний |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Проверить правильность выполнения домашней работы
|
(Ф) I . Проверка домашнего задания. 2. Теоретический опрос: — Сформулируйте первый признак подобия треугольников. — Чему равно отношение периметров подобных треугольников? — Какие треугольники называются подобными? — Сформулируйте теорему об отношении площадей подобных треугольников. 3. Найти пары подобных треугольников (устно):
|
|
Продолжение
|
П этап. Решение задач по готовым че тежам |
||||||||||||
|
Цель деятельности |
Задания для самостоятельной аботы |
|||||||||||
|
На простых задачах проверить уровень усвоения первого признака подобия треугольников |
(И) Учащиеся самостоятельно решают данные задачи, затем решение каждой задачи выносится на доску. Проводится обсуждение решений и осуществляется самооценка.
Рис. 2Рис. З Ответ: ВС = 3,2, 224 Ответ: З. Дано: а ll Ь. Найти: х, у. 4. Найти: BD. а
Рис. 4 Рис. 5 Ответ:х =4 Ответ: BD = 8.
В Рис.
6 Ответ.• со = 4, во; 12 Ответ.• 15 |
|||||||||||
|
III этап. Решение задач |
||||||||||||
|
Цель деятельности |
Деятельность чителя |
Деятельность чащихся |
|
|||||||||
|
|
2 |
З |
|
|
||||||||
|
Отработать применение первого признака подобия при решении задач |
(ф) 1. Решите № 556. 2. Решите № 557 (а). |
.N2 557 (а). Краткое решение:
22 Ответ: АС = 17,5 см. |
|
17,5 (см) |
||||||||
Окончание
|
|
2 |
3 |
|
|
|
З. Самостоятельно решите № 557 (б), 552 (в) в парах. (Затем проверка на Доске.) 4. Решите задачу: Диагонали трапеции ABCD с основаниями AD и ВС пересекаются в точке О. Периметры треугольников ВОС и AOD относятся как 2 : З, АС = 20. Найдите длины отрезков АО и ОС |
ЛЬ 557 (6). Краткое решение: МВС ЛОЕ.
= 15 (см), DE — = 6 (см). О 12 DE 8 8 15- (см). Ответ: 5 см, 6 см. ЛЕ 552 (в). Краткое решение (рис. 461) • Пусть АО = х см, тогда ОС = АС — АО = 15 — х (см).
МОВ Д СО СО - О 15-х 24 1 20х = 1440; х = 12 (см), то есть АО = 12 см. Ответ: АО = 12 см. Решение:
накрест лежащие при параллельных прямых AD и ВС и секущих АС и BD), во ос вс Рис. 8 тогда то есть ОС : т = 2 : З, Т = 1,5ОС. Так как 20, то АС = ОА + ОС = 1,50С + ОС = 20, откуда ОС = 8, тогда 12. Ответ: АО- 12, ОС=8 |
|
|
IV этап. Итоги |
ока. Ре лексия |
||
|
Деятельность чителя |
Деятельность ЧщИХСЯ |
||
|
— Оцените свою работу на уроке. — Какие трудности возникли у вас при решении задач? — Кто может с полной уверенностью сказать, что понял, как применять пе вый п изнак подобия е гольников п и ешении задач? |
(И) Домашнее задание: повторить п. 59; решить задачи № 552 (а, б), 557 (в), 558, 556 |
||
У р 33. Тема: ВТОРОЙ И ТРЕТИЙ ПРИЗНАКИ ПОДОБИЯ ТРЕУГОЛЬНИКОВ
|
Цель деятельности чителя |
Создать условия для доказательства второго и третьего признаков подобия треугольников |
|
|
Те мины и понятия |
П опо циональные от езки, отношение, п опо ции, сходственные сто оны, коэ ициент подобия |
|
|
Плани емые ез льтаты |
||
|
П едметные мения |
Униве сальные чебные действия |
|
|
Умеют демонстрировать знание основных понятий, применять полученные знания для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности |
Познавательные: осуществляют поиск необходимой информации для выполнения учебных заданий с использованием учебной литературы. Регулятивные: умеют адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения, контролируют действие партнера, осуществляют самоанализ и самоконтроль. Коммуникативные: умеют вступать в речевое общение, участвовать в диалоге. Личностные: п оявляют познавательный инте ес к из чению п едмета |
|
|
О ганизация п ост анства |
||
|
Фо мы аботы |
Ф онтальная Ф ; индивид альная И |
|
|
Образовательные ес сы |
• Учебник. • Задания для индивид альной аботы |
|
|
этап. Ак ализация знаний чащихся |
||
|
ель деятельности |
Задания для самостоятельной аботы |
|
|
Проверить степень усвоения первого признака подобия треугольников
|
1. Проверка домашнего задания. 2. Самостоятельная работа с взаимопроверкой. (Решение дано на закрытой Доске.)
Рис. Рис. 2 МСВ
|
|
Продолжение
|
П этап. Изучение нового материала |
|||||
|
Цель деятельности |
Совместная деятельность |
||||
|
Доказать второй и третий признаки подобия треугольников |
(Ф) Второй признак подобия треугольников. Теорема. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны. Учащиеся записывают в тетраДях план-конспект Доказательства теоремы. Третий признак подобия треугольников. Теорема. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны. Учащиеся записывают в тетраДях тан-конспект Доказательства теоремы |
||||
|
111 этап. Закрепление изученного материала |
|||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|||
|
Отработать применение изученных признаков при решении простых задач |
(ФМ) Решение Докажите, если катеты
|
задач что два одного 15 С Рис. |
на доске и в тетради. прямоугольных треугольника из них пропорциональны ОА =6 см, АС = 15 см, см, 12 см. Найдите CD. Рис. З
Найдите АВ и CD 4 |
подобны, катетам другого. ОВ=9 см, 5 см; см. |
Решение: 1) OD
= ОВ + ОС = Т + АС = 6+ 15 = 21 (см). 2) Угол О общий для треугольников ВОА и СОД ОВ 9 з т 6 3 3)
ДВОА ДСО по П признаку подобия треугольников. 4) Ответ: 28 см. Решение: 1) В треугольниках DOC и АОВ угол О — общий DO 5 1 со и Т - 15 - З'ОВ - З бия треугольников. 2) пусть DC = х, тогда АВ = 24 - х. DC 3), значит, DC= 6 см, АВ = 18 см.
Ответ: 18 см и 6 см |
|
IV этап. Итоги урока. Рефлексия |
|
|
Деятельность учителя |
Деятельность учащихся |
|
Сформулируйте признаки подобия треугольников. — Составьте список вопросов, на которые мы будем отвечать на следующем уроке. Как вы думаете, зачем его составлять? |
(И) Домашнее задание: п. 62, 63, вопросы 6, 7; решить задачи № 559, 560, 561. Творческое задание: увеличить или уменьшить картинку |
У р к 34. Тема: РЕШЕНИЕ ЗАДАЧ НА ПРИМЕНЕНИЕ ПРИЗНАКОВ ПОДОБИЯ ТРЕУГОЛЬНИКОВ
|
Цель деятельности учителя |
Создать условия для формирования у учащихся навыков применения признаков подобия треугольников при решении задач |
|
|
Термины и понятия |
Пропорциональные отрезки, отношение, пропорции, сходственные стороны, коэффициент подобия |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Умеют демонстрировать знание основных понятий, применять полученные знания для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности |
Познавательные: осуществляют поиск необходимой информации для выполнения учебных заданий с использованием учебной литературы. Регулятивные: умеют адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения, контролировать действие партнера; осуществляют самоанализ и самоконтроль. Коммуникативные: умеют вступать в речевое общение, участвовать в диалоге. Личностные: проявляют познавательный интерес к изучению предмета |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные ресурсы |
• Учебник. • Задания для индивидуальной работы |
|
|
ЭТаП. Проверка домашнего задания |
||
|
цель деятельности |
Совместная деятельность |
|
|
Выявить трудности, возникшие при выполнении домашнего задания; оценить рисунки учащихся и список вопросов |
(Ф) 1 . Обсудить вопросы учащихся по домашней работе. 2. Оценить рисунки учащихся. З. Заслушать список вопросов, которые подготовили учащиеся. (И) 4. Провести 5-минутный тест (см. Ресурсный материал). Ответы к тесту: 1-й вариант: 1. Подобными; 2. К = 2; З. х = 7. 2-й вариант: 1. Коэффициентом; 2. К =З; З. х = 5 |
|
Продолжение
|
П этап. Решение задач |
|||||
|
Цель деятельности |
|
Совместная деятельность |
|
||
|
Научить применять признаки подобия при решении задач |
1. Решение задач по 1) Найти: Щ, ВС.
Рис. ответ: Щ = 71 0 , 4) Найти: ВС.
Рис. 4
З Проверить решения задач Индивидуально поработать 2. Дополнительные задачи. 1) Диагональ АС трапеции АВ = 25 см, ВС = 20 см, Ответ : SAB(D= 204 см 2. 2) Угол В треугольника Найдите стороны треугольника Ответ: АС = 9 см, АВ = |
готовым чертежам. с, = 15 см.
по готовым ответам. с теми детьми, которые ABCD (АВ П CD) делит ее АС = 15 см. АВС в два раза больше угла АВС 66 см, ВС = 3 зд см |
2) Найти: ZC, ZCl. в
А 12c С Ответ: ZC = 5) НаЙти.• АВ, ЛС
Рис. 5 Ответ:АВ= Учащиеся, справившиеся допустили ошибки на два подобных А. Биссектриса угла |
Рис. 2 600.
со всеми при решении треугольника. Найдите В делит сторону |
3) Найти: ВМ.
Рис. З Ответ: ВМ=6 см. задачами, решают дополнительные. задач. площадь трапеции ABCD, если АС на части AD = 6 см и CD = З см. |
Окончание
|
|
III этап. Итоги урока. Рефлексия |
|
|
Деятельность учителя |
|
Деятельность учащихся |
|
— Оцените свою работу на уроке. Какие трудности возникли при решении и почему? — За что бы ты себя похвалил на уроке? — Что изменил бы в своих действиях на уроке? — Что бы ты изменил на уроке в последующем? — Что тебе понравилось на уроке больше всего? |
|
(И) Домашнее задание: решить задачи № 562, 563, 604, 605 |
Тест
«Признаки подобия треугольников»
|
|
|
|
Вариант 1 |
Вариант П |
|
|
2 |
|
I . Вставить пропущенное слово. Два треугольника
называются |
1. Вставить пропущенное слово. Число К, равное отношению сходственных сторон подобных
треугольников, называется |
|
2. Найти коэффициент подобия.
Ответ: |
2. Найти коэффициент подобия. 12
9 Ответ: |
Окончание
|
|
2 |
|
З. Найти х, если АВ = 21, ВС =
Ответ: |
3. Найти х, если АВ = 10, 40, РС = 20.
Ответ: |
У р о к 35. Тема: РЕШЕНИЕ ЗАДАЧ НА ПРИМЕНЕНИЕ ПРИЗНАКОВ ПОДОБИЯ ТРЕУГОЛЬНИКОВ
|
Цель деятельности учителя |
Создать условия для совершенствования навыков решения задач на применение признаков подобия треугольников для подготовки чащихся к конт ольной аботе |
||
|
Те мины и понятия |
П опо циональныео езки, отношение, п опо ции, сходственные сто оны, коэ |
ициент подобия |
|
|
Плани емые ез льтаты |
|||
|
П едметные мения |
Униве сальные чебные действия |
||
|
Умеют демонстрировать знание основных понятий, применять полученные знания для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности |
Познавательные: осуществляют поиск необходимой информации для выполнения учебных заданий с использованием учебной литературы. Регулятивные: умеют адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения, контролировать действие партнера, работать в группе, осуществлять самоанализ и самоконтроль. Коммуникативные: вступают в речевое общение, участвуют в диалоге. Личностные: п оявляют познавательный инте ес к из чению п едмета |
||
|
О ганизация п ост анства |
|||
|
Фо мы аботы |
Ф онтальная Ф ; индивид альная И ; пповая |
||
|
Образовательные ес сы |
• Учебник. • Задания для г пповой и индиви альной аботы |
||
|
этап. П ове ка домашнего задания |
|||
|
ель деятельности |
Совместная деятельность |
||
|
|
2 |
||
|
Проверить уровень усвоения признаков подобия гольников |
I . Ответить на вопросы учащихся. 2. П ове ить выполнение домашнего ±адания. |
||

![]()
![]() ПроДол.жение
ПроДол.жение
|
|
2 |
|
|
|
CN 2) ANCD ДСКВ (по двум углам), следовательно, СК 2
З), то есть АК: : 2; —, то есть 2. Значит, , что и требовалось доказать АЛГ З СК 2 кс 4 |
|
|
П этап. Решение задач |
||
|
Цель деятельности |
Деятельность чителя |
Деятельность чащихся |
|
Совершенствовать навыки решения задач на применение признаков подобия треугольников; подготовить учащихся к контрольной работе |
(Г) Класс делится на группы по 3—4 человека. Учитель при необходимости оказывает консультативную помощь. Задачи . 1. В прямоугольном треугольнике АВС И = 40 0 , ZB = 900 , а в треугольнике ЛПК углы М, N, К относятся как 5 : 9 АВ = З см, 9 см. Найти: а) ВС : КМ, 6) : 2.
20 см. Найти: АС.
Рис. 4 З. В параллелограмме ABCD АЕ — биссектриса угла А. Стороны параллелограмма АВ и ВС относятся как 4 : 9. АЕ пересекает диагональ BD в точке К. Найти отношение ВК : kD. |
Краткое решение задач: 1. ZM: ZN: Л = 5 : 9 : 4, ZM+ ZN+
а) так как АВ : ЛК = : З, ТО ВС : З. 6) snc: SMNk= (АВ : : 9. В) РАВС : РЛОЖ Ответ : а) : З; б) 1 : 9; в) 1 : З. 2. ЛАВС двлт по двум углам (ZB - общий, ZBAC = ZBM№). SABC • Ятк= 49 : 25 =К2 , К- — = АС : 5 Ответ: 28 см.
Рис. 5 то ВЕ : ВС = 4 : 9. ВЕ : AD = 4 : 9 (ВС = АД как противолежащие стороны параллелограмма). МИО ДЕКВ по двум углам (ОКЕ = ИО, ЗЕК = ZkAD), тогда ВК: 10 = ВЕ : 9. Ответ: 4 : 9. |
Окончание
|
|
2 |
|
3 |
|
|
|
4. В трапеции ABCD основания ВС и AD равны 2 см и 8 см, а диагональ АС равна 4 см. В каком отношении делит диагональ АС площадь трапеции? 5. Прямая MN пересекает стороны АВ и ВС треугольника АВС в точках Ми лт соответственно так, что ВС = 2МВ, АВ = 2NB,
Найти: а) РАЮ : Рмм•, 6) : явм•, в) ММ : АС |
В Рис. 7 а)
Рвлт : РАВС 6) Ответ: а) 1 : 2; б) 4 : |
ЛАВС -- ОСА по двум пропорциональ- ным сторонам и углу между ними (ВС : АС = АС : 2; Д = П), отсюда ,SABc: Soc= (ВС : АС) 2 — 4
АВ = 2NB = АВ = lOx.
ZMBN= СВА, таким образом, ЛАВС ДМВМ. - 4 1; в) : 2 |
|
|
этап. Итоги урока. Рефлексия |
||||
|
Деятельность учителя |
Деятельность учащихся |
|||
|
— Оцените свою работу и работу группы. — Какая задача оказалась для вас трудной и почему? |
(И) Домашнее задание: решить задачи. I. Высота CD прямоугольного треугольника АВС делит гипотенузу АВ на части AD = 16 см и BD = 9 см. Докажите, что MCD ЛСВД и найдите высоту CD. 2. Точки М и лг лежат на сторонах АС и ВС треугольника АВС соответственно, АС = 16 см, ВС = 12 см, СМ = 12 см, CN= 9 см. Докажите, что вс |
|||
У к 36. Тема: КОНТРОЛЬНАЯ РАБОТА ЛЬ З
|
Цель деятельности учителя |
Создать условия для проверки знаний, умений и навыков учащихся по усвоению и применению изученного материала |
|
Термины и понятия |
Пропорциональные отрезки, отношение, пропорции, сходственные стороны, коэффициент подобия |
Продолжение
|
Плани емые ез льтаты |
||
|
П едметные мения |
Униве сальные чебные действия |
|
|
Умеют демонстрировать знание основных понятий, применять полученные знания для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности |
Познавательные: проводят сравнение, сериацию и классификацию по заданным критериям. Регулятивные: вносят необходимые коррективы в действие после его завершения на основе его учета характера сделанных ошибок; осуществляют самоанализ и самоконтроль. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: понимают важность и необходимость знаний для человека |
|
|
О ганизация п ост анства |
||
|
Фо мы аботы |
Индивид альная (И |
|
|
Образовательные ес сы |
• Учебник. • Задания для индивид альной аботы |
|
|
этап. Выполнение конт ольной аботы |
||
|
ель деятельности |
Задания для ко ольной аботы |
|
|
|
2 |
|
|
Проверить знания, умения и навыки по изученному материалу |
Найти: а) ОВ•, 6) АС : ВО, в) SAoc: SBOD• Рис. 1 D 2.
В треугольнике АВС АВ = 4 см, ВС = 1 см, АС = 6 см, а в треугольнике
MNk МК = 8 см, 3. Прямая пересекает стороны треугольника АВС в точках Ми К соответственно так, что МК АС, ВМ : АМ= 1 : 4. Найдите периметр треугольника ВМК, если периметр треугольника АВС равен 25 см. 4*. В трапеции ABCD (О и ВС — основания) диагонали пересекаются в точке О, AD = 12 см, ВС = 4 см. Найдите площадь треугольника ВОС, если площадь треугольника АО равна 45 см2
Рис. 2 2.
В МВС 12 см, ВС= 18 см, |
|
[фоДол.жение
|
|
2 |
|
|
|
3. Отрезки АВ и CD пересекаются в точке О так, что ZACO = ZBDO, АО : ОВ = 2 : 3. Найдите периметр если периметр треугольника ВО равен 21 см. 4*. В трапеции ABCD (AD и ВС — основания) диагонали пересекаются в точке О , SАОГ)= 32 см , основание трапеции, если большее из них равно 10 см. Решение заданий контрольной работы Ва р иа нт 1 1.
МОС ДВО по двум углам. АО : ВО = СО : DO 2.
АВ : МК = : 2, ВС : клГ
= в а) лвмк- ДВАС по двум углам ВМ: ВА = МК : АС = вк : ВС= - . 5 б) Рвмк: РАвс= : 5, значит, Рвмк= 5 см. Ответ : 5 см.
6) ВО
: DO = ОС : Т - В) :
DOA D Ответ : 5 см2 Рис. 4 Ва ри а нт П 1.
ДМРЕ ДММ< по двум углам. МР : МЕ : МК = МК = 9. РЕ : ЛК = 2
: З. 2. АВ : 2, ВС : ЛК = 2, = ЛАВС- ДМЛК. АС : МК = 2 = АС = 14 см, С = Zk = 60 0 . Ответ : АС = 14 см, ZC = 60 0 . а) МСО ДОО по двум
углам = АС : О = СО : DO = АО : ВО = 2 : З. 6) : Роо=2 : З Ответ: 14 см.
|
треугольника АСО, = 8 см . Найдите меньшее 180 0 -(ZM+ Zk) = 40 0 . |
![]() Окончание
Окончание
|
1 |
2 |
|
|
|
4 в) ВС : AD = К = 0,5, значит, ВС = 5 см Рис. |
|
|
|
этап. Итоги ока |
|
|
|
еятельность чителя |
еятельность чащихся |
|
|
|
И омашнее задание: повто ить 2 главы VIl и тео ем Фалеса |
У рок 37. Тема: СРЕДНЯЯ ЛИНИЯ ТРЕУГОЛЬНИКА
|
Цель деятельности чителя |
Создать условия для доказательства теоремы о средней линии треугольника и свойства медиан треугольника; для применения этих свойств в п оцессе ешения задач |
|
|
Термины и понятия |
Пропорциональные отрезки, отношение, пропорции, сходственные стороны, коэффициент подобия, средняя линия треугольника |
|
|
Плани емые ез льтаты |
||
|
П едметные мения |
Униве сальные чебные действия |
|
|
Владеют базовым понятийным аппаратом по основным разделам содержания |
Познавательные: понимают и используют математические средства наглядности для иллюстрации, интерпретации, аргументации; устанавливают причинно-следственные связи, строят логическое рассуждение, делают умозаключения и выводы. Регулятивные: принимают и сохраняют цели и задачи учебной деятельности. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве; умеют ясно, точно, грамотно излагать свои мысли в устной и письменной речи. Личностные: п являют познавательные инте ес к из ЧеНИЮ п едмета |
|
|
О ганизация п ост анства |
||
|
Фо мы аботы |
Ф онтальная Ф ; индиви альная И ; г пповая Г |
|
|
Образовательные ес сы |
• Учебник. • Задания для индивид альной и г пповой аботы |
|
|
этап. Активизация знаний чащихся |
||
|
ель деятельности |
Совместная деятельность |
|
|
Выявить трудности, возникшие при решении задач в конт ольной аботе |
1. Сообщить результаты выполненной работы. 2. Обсудить решения задач, с которыми не справились большинство учащихся. З. П едложить выполнить або над ошибками самостоятельно дома |
|
|
|
П этап. Мотивация к деятельности |
|
|
Цель деятельности |
Постановка учебной задачи |
|
|
Подготовить учащихся к введению понятия средняя линия треугольника |
Повторить теоретический 1. |
материал в процессе решения задач по готовым чертежам.
Доказать: а) ДОЕ ДСАВ•,Доказать: а) ВО : 0D = со : т; 6) АВ DE.6) DO : ВО =2, если ВС = 2 Рис. 2 |
|
|
|
III этап. Учебно-познавательная деятельность |
|
|
|
Изучение нового материала |
|
Цель деятельности |
|
Совместная деятельность |
|
|
|
2 |
|
Ввести понятие средней линии трапеции и доказать теорему о средней линии трапеции |
(Ф/И) 1. Определение средней линии треугольника. Определение. Отрезок, соединяющий середины двух сторон треу гольника, называется средней линией треугольника. На доске и в тетрадях рисунок из учебника на с. 145 и запись: «Если АМ= МВ и CN= NB, то ДТ— средняя линия ДАВС». (Г) 2. Творческое задание. Работа осуществляется в группах с последующим обсуждением решения. — Исследуйте, какими свойствами обладает средняя линия треугольника. 3. Оформление теоремы о средней линии треугольника с доказательством на доске и в тетрадях. 4. Решение задач № 564, 565 (устно, рисунки на Доске выполнены заранее).
Найти: Р ABlCl Рис. З Решение. 1) АД, ВС, АС] — средние линии ЛАВС, значит, АС =—АС = 3,5 см, =-ВС = 2,5 см; = — АВ = 4 см 2
|
|
Продолжение
|
|
2 |
||
|
|
.N2 565.
дано: ABCD - прямоугольник, АС п BD = О, ОН Ш О, ОН = 2,5 см. Найти: АВ. Решение: 1) Рассмотрим МОН и MCD: И — общий, ZD = 900 , следовательно, МОН MCD, Рис. 4 АО ОН он следовательно, Так как О — середина АС, то АО = — АС, значит, --. 20Н = СО, 2 • 2,5 = СО, CD=5 см. ОС CD (Г) 5. Творческое задание. Задача № 1, с. 146 (учащиеся работают в группах по 3—4 человека). Доказать, что медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2 : 1, считая от вершины. 6. Решение задачи с целью закрепления свойства медиан треугольника (устно).
пересекаются в точке О. Найти: АО + ОВ + СО Рис. 5 |
||
|
IV этап. Решение задач |
|||
|
Цель деятельности |
Деятельность учителя |
|
Деятельность учащихся |
|
|
2 |
|
3 |
|
Совершенствовать навыки решения задач на применение знаний о подобных треугольниках |
(Ф/И) Решить на доске и в тетради № 567 и 570 |
Рис. 6 Доказательство: 1) Рассмотрим ДАВС следовательно, ДАВС |
Дано: ABCD — четырехугольник, М, N, К, Е — середины сторон. Доказать: МУКЕ — параллелограмм. вм вм и AMBN: ZB — общий, = — (по условию), АВ ВС 2 -- &VfBN (по двум сторонам и углу между ними), |
Окончание
|
|
2 |
|
З |
|
|
|
|
следовательно, MN = — АС и Ш АС. 2) Рассмотрим ЛАВС. КЕ — средняя линия MDC (по
определению), значит,
КЕ АС АТКЕ— параллелограмм по признаку, что и требовалось доказать.
Дано: ABCD — параллелограмм, АС = 8 см, Ме АВ, МВ, МТЛ АС = О. Найти: АО, ОС. 7 Решение: 1) Рассмотрим МВД DM, АЕ — медианы и АЕ п DM = О, по свойству медиан АО : ОЕ=2 : 1. 2) Так как (свойство диагонали параллелограмма) АЕ = 9 см, тогда АО = 6 см, З см, отсюда ОС = ОЕ + ЕС=З 12 СМ. Ответ: 6 см, 12 см. |
|
|
V этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
|
Деятельность учащихся |
|
|
— Составьте синквейн к уроку. — Оцените свою работу |
|
(И) Домашнее задание: вопросы 8, 9, с. 59; № 565, 566, 571 |
|
У рок 38. Тема: СРЕДНЯЯ ЛИНИЯ ТРЕУГОЛЬНИКА
|
Цель деятельности учителя |
Создать условия для совершенствования навыков решения задач на применение теоремы о средней линии треугольника и свойства медиан треугольника |
|
Термины и понятия |
Пропорциональные отрезки, отношение, пропорции, сходственные стороны, средняя линия треугольника, медианы треугольника |
Продолжение
|
|
|
||||||||||||||||||||||||||||||||||||||||||
Окончание
|
|
2 |
|
|
|
Найти: ММ Рис. 5 Рис. 4
6) snc= 369
см2 В Рис. 6 Ответ: а) SABB — 15 см 2 •, б) = 12 см 2 ; в) — 6 см2 (Ф) 2. Решить у доски и в тетрадях № 568 (а), 617 |
|
|
III этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
— Оцените свою работу. — Что пол чилось на оке, что вызвало зат днения? Почем ? |
(И) Домашнее задание: решить № 568 (б), 61 8 |
|
Самостоятельная работа
![]()
![]()
![]() 1. 2. З. 4.
дано: FMN-
1. 2. З. 4.
дано: FMN-
прямоугольник, 24. к
м
Ответ ы : 1. Рдммк![]() ЛЕТЕ 12,
ЛЕТЕ 12, ![]() ЕКАЛ 120.
ЕКАЛ 120.
У р о к 39. Тема: ПРОПОРЦИОНАЛЬНЫЕ ОТРЕЗКИ В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ
|
Цель деятельности чителя |
Создать условия для рассмотрения задачи о пропорциональных отрезках в прямоугольном треугольнике |
|
|
Те мины и понятия |
П опо циональные от езки, отношение, п опо ции, с еднее п опо циональное |
|
|
Плани емые ез льтаты |
||
|
П едметные мения |
Униве сальные учебные действия |
|
|
Владеют базовым понятийным аппаратом по основным разделам содержания |
Познавательные: понимают и используют математические средства наглядности для иллюстрации, интерпретации, аргументации; устанавливают причинно-следственные связи, строят логическое рассуждение, делают умозаключения и выводы. Регулятивные: принимают и сохраняют цели и задачи учебной деятельности. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве; умеют ясно, точно, грамотно излагать свои мысли в устной и письменной речи. Личностные: п оявляют познавательный инте ес к из чению п едмета |
|
|
О ганизация п ост анства |
||
|
Фо мы аботы |
Фронтальная (Ф); индивидуальная (И); групповая (Г) |
|
|
Образовательные ес сы |
• Учебник. • Задания для онтальной аботы |
|
|
этап. Активизация знаний чащихся |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Выявить трудности при выполнении домашнего задания; проверить умение применять изученнькй материал при решении простейших задач |
(ФМ) 1. Проверка домашнего задания. Один из учеников у доски показывает решение № 618.
Доказать: ВЕ = ЕЕ = DF. Доказательство: 1) Рассмотрим ДАВС. АЛЛ, ВО — медианы, по свойству медиан ВЕ : ЕО = 2 : 1. 2) Аналогично в АСТ DF: FO=2: 1. Рис. 3) Так как в параллелограмме ABCD диагонали точкой пересечения делятся пополам, то ВО - —ОД ВЕ + ЕО = Т + Т, то есть ВЕ = ЕЕ = дГ. 2х = х + lx = 2х, что и требовалось доказать. (И) 2. Самостоятельная работа. Вариант 1 Площадь ромба 48 см 2 . Найдите площадь четырехугольника, вершинами которого являются середины сторон данного ромба. Вариант П Площадь прямоугольника равна 36 см 2 . Найдите площадь четырехугольника, вершинами которого являются середины сторон данного п ямо голышка |
|
|
|
П этап. Мотивация к деятельности |
|||||
|
Цель деятельности |
Постановка чебной задачи |
|||||
|
При решении задач по готовым чертежам подготовить учащихся к восприятию новой темы |
(Ф) Решение задач по готовым чертежам с целью подготовки учащихся к восприятию нового материала.
Доказать:ВД а) ДАО ДВСО, 6) ДАШ) МСВ. А Рис. 2Рис. З |
|||||
|
|
III этап. Из чение нового мате нала |
|||||
|
Цель деятельности |
Совместная деятельность |
|||||
|
Ввести понятие среднего геометрического двух отрезков, отработать решение задач, помочь в построении доказательства |
. Среднее геометрическое двух отрезков. Ввести понятие среднего пропорционального (среднего геометрического) двух отрезков. Определение. Отрезок ХУ называется средним пропорциональным (средним геометрическим) для отрезков АВ и СД если ХУ = АВ.СТ 2. Решение задач (устно). 1. Найти длину среднего пропорционального отрезков МЛ/и КАР, если ММ = 9 см, КР = 16 см. 2. Среднее пропорциональное отрезков АВ и CD равно 10, а разность их длин равна 21. Найти длины отрезков АВ и CD. (Г) 3. Творческое задание. (Класс разбить на группы.) Задача № 2 (с. 146—147, п. 65 учебника), утверждения и 2 0 (с. 147, п. 65). 1 -я г ру п п а : Доказать, что высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику. 2-я г ру п п а : Доказать, что катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла. (Данные заДачи желательно Дать группам на отдельных карточках для обеспечения максимально самостоятельного поДхоДа к- ешению задач. |
|||||
|
|
IV этап. Зак епление из ченного мате иала |
|||||
|
Цель деятельности |
Деятельность чителя |
Деятельность чащихся |
||||
|
|
2 |
|
||||
|
Закрепить полученные знания |
(ФМ). 1. Решить у доски и в тетрадях № 572 (а, в). 2. Решить № 573 (устно). З. Решить № 575 |
Г•Г2 572 (а, в). а)
С = ас. + bc= 25 + 16=41
|
в)
ас = 18. |
; b2 = с • И., 144 = с • 6, С 24. 576 =а2 + 144 ; а2=432; ; = с • ас; 432 = 24 • ас; |
||
|
Цель деятельности учителя |
Создать условия для совершенствования навыков решения задач на применение теории подобных треугольников |
|
|
Термины и понятия |
Пропорциональные отрезки, отношение, пропорции, среднее пропорциональное |
|
|
Планируемые ез льтаты |
||
|
Предметные умения |
Универсальные чебные действия |
|
|
Владеют навыками устных, письменных, инструментапьных вычислений |
Познавательные: умеют видеть математическую задачу в контексте проблемной ситуаций. Регулятивные: умеют адекватно оценивать правильность или ошибочность выполнения учебной задачи. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные:
проявляют креативность мышления, инициативность, находчивость, |
|
|
Организация прост анства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные сурсы |
• Учебник. • Задания для индив альной работы |
|
Окончание
|
|
2 |
|
З |
|
|
|
|
|
Решение: ) АС2 + ВС2 = АВ2 •, (3х)2 + (4х)2 = 25х2
=
АВ 50 АВ Ответ: 18 мм; 32 мм |
З : 4, АВ = 50 мм, CD ШАВ. 2500 ЗО мм, ВС =40 мм 1600 — = 32 50 |
|
|
V этап. Итоги |
у ока. Ре лексия |
|
|
|
Деятельность учителя |
|
Деятельность учащихся |
||
|
— С какими понятиями познакомились на уроке? — Какой этап урока оказался для вас наиболее сложным? — Составьте синквейн к уроку |
|
(И) Домашнее задание: решкгь № 572 (б), 574, 576 |
||
У р о к 40. Тема: ПРОПОРЦИОНАЛЬНЫЕ ОТРЕЗКИ В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ
ИроДолжение
|
этап. Активизация знаний чащихся |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Выявить трудности при выполнении домашнего задания |
(Ф/И) Проверка домашнего задания. I. Вызвать троих учащихся для решения домашнего задания. 2. Подготовить доказательства следующих свойств прямоугольного треугольника: 1) Высота прямоугольного треугольника, проведенная к гипотенузе, делит его на два подобных треугольника, каждый из которых подобен данному. 2) Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой. З) Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного ме катетом и высотой, п оведенной из ве шины п ямого гла |
||
|
П этап. Решение по готовым че тежам |
|||
|
ель деятельности |
еятельность чителя |
еятельность чащихся |
|
|
На простых задачах закрепить знания о пропорциональных отрезках |
(И) Учащиеся решают проверяют их у доски.
з. в
Рис. м Рис. 4 |
задачи самостоятельно, затем Найти: СН. Найти: МС. Найти: АВ, ВС. Найти: х; у; z |
Ответы : 1. 10. 2. мс-
|
ПроДол.жение
|
Ш этап. Решение задач |
||
|
ель деятельности |
еятельность чителя |
еятельность чащихся |
|
Совершенствовать навыки решения задач |
(ФМ) Учащиеся решают у доски и в тетрадях № 577, 614 |
ЛР2 577. в дано: МВС, АВ = 5 см, ВС = 12 см, АС = В мм, ОШ АС. Найти: О, СД
13' 13 614.
Решение: 1) по теореме ПифагораВО = АВ2 +AD2•, В» = 36 + 16 = 52; 246 см. 2) Рассмотрим MDC и ДВАД ZD = И = 900 ;ZC = О, следовательно, .AD DC АС ДОС ДВО (по двум углам), следовательно, ВА О BD
2 По теореме Пифагора ВС2 = ВН2 + СН2 •, ВС2 =42+ З— З
, следовательно, ВС = 61 см. 9 9 Ответ: 246 см; 2— см; 2 61 см з З |
Окончание
|
IV этап. Итоги |
ока. Ре лексия |
|
еятельность чителя |
еятельность чащихся |
|
Подведите самостоятельно итоги урока. Какие задачи вызвали вас наибольшее зат днения? Почем ? |
(И) Домашнее задание: № 607, 623 |
У р о 41. Тема: ИЗМЕРИТЕЛЬНЫЕ РАБОТЫ НА МЕСТНОСТИ
|
Цель деятельности чителя |
Создать условия для применения подобия треугольников в измерительных работах на местности |
||
|
Те мины и понятия |
П опо циональные от езки, отношение, п опо ции, с еднее п опо циональное |
||
|
Плани емые ез льтаты |
|||
|
П едметные мения |
Униве сальные чебные действия |
||
|
Владеют навыками устных, письменных, инструментальных вычислений |
Познавательные: умеют видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни. Регулятивные: умеют адекватно оценивать правильность или ошибочность выполнения учебной задачи. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: проявляют креативность мышления, инициативность, находчивость, активность п и ешении геомет ических задач |
||
|
О ганизация п ост анства |
|||
|
Фо мы аботы |
Ф онтальная Ф ; индиви альная И |
||
|
Образовательные ресурсы |
• Учебник. • Задания для индивидуальной работы. • Исто ические сведения |
||
|
этап. Активизация знаний чащихся |
|||
|
ель деятельности |
Задания для самостоятельной аботы |
||
|
Проверить уровень сформированности знаний по изученной теме |
1. Проверка домашнего задания. 2. Выполнение теста (см. Ресурсный материал) |
||
|
П этап. Из чение нового мате мала |
|||
|
Цель деятельности |
еятельность чителя |
Деятельность чащИхся |
|
|
|
2 |
З |
|
|
Ознакомить учащихся с практическим применением подобия |
— Прочитайте самостоятельно текст «Определение расстояния до недоступной точки» на с. 151 учебника. Использ я задач № 583 и ис. 204 с. 155), составьте план |
ВозможныЙ пиан: 1) На местности выбрать точку А и точку Д на берегу реки так, чтобы АЩ было перпендикулярно берегу. В— точка на противоположном бе е |
|
Окончание
|
|
2 |
З |
|
|
|
действий для определения ширины реки. — Решите задачу № 582. один из учащихся работает у доски, остальные в тетраДях |
2) На берегу реки выбрать точку С, отличную от Д. 3) Измерить углы ДАС и АСВ. 4) На листе бумаги выполнить рисунок в некотором масштабе и провести прямую Щ С] параллельно ВВ. 5) Вычислить АД а затем ВВ. АВ ЛЬ 582. АВ АС ДА РС] ЛАВС (по построению). Тогда АСАД 4200-7,2 = 48 (м). 6,3 Ответ: 48 м |
|
|
III этап. Исто ические сведения |
|||
|
ель деятельности |
Совместная деятельность |
||
|
Ознакомить учащихся с историчесмми фатами о подобии, дошедшими до наших дней |
(Ф) (См. Ресурсный материал) |
||
|
IV этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
— Какие факты вы для себя открыли? — Оцените свою аб на оке |
(И) Домашнее задание: № 580, 581 ; подготовить сообщение о применении подобия в быту |
||
![]()
![]() 1) Выберите верное
соотношение между элементами прямоугольного треугольника. 2) Сколько
пар подобных треугольников изображено на рисунке?
1) Выберите верное
соотношение между элементами прямоугольного треугольника. 2) Сколько
пар подобных треугольников изображено на рисунке?
3)
![]() Треугольники BMN и АВС, изображенные на рисунке:
Треугольники BMN и АВС, изображенные на рисунке:
а) подобны по двум углам;
![]() б) подобны по двум пропорциональным
сторонам и углу между ними;
б) подобны по двум пропорциональным
сторонам и углу между ними;
в) подобны по трем пропорциональным сторонам;
г) не подобны.
4) На рисунке в прямоугольном треугольнике АВС длина катета ВС равна
![]()
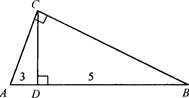
ответы : 1) г; 2)
г; 3) 6; 4) 246![]()
Исторические сведения
•
![]()
![]() Уже в XVI в. нужды
землемерия, строительства и военного дела привели к созданию рукописных
руководств геометрического содержания. Первое дошедшее до нас сочинение такого
рода носит название «О земном верстании, как землю верстать». Оно является частью
«Книги сошного письма», написанной, как полагают, при Иване IV в 1556 г.
Сохранившаяся копия относится к 1629 г. При разборе Оружейной Палаты в Москве в
1775 г. была обнаружена инструкция «Устав ратных, пушечных и других дел,
касающихся до военной науки», изданная в 1 607 и 1621 годах и содержащая
некоторые геометрические сведения, которые сводятся к определенным приемам
решения задач на нахождение расстояний.
Уже в XVI в. нужды
землемерия, строительства и военного дела привели к созданию рукописных
руководств геометрического содержания. Первое дошедшее до нас сочинение такого
рода носит название «О земном верстании, как землю верстать». Оно является частью
«Книги сошного письма», написанной, как полагают, при Иване IV в 1556 г.
Сохранившаяся копия относится к 1629 г. При разборе Оружейной Палаты в Москве в
1775 г. была обнаружена инструкция «Устав ратных, пушечных и других дел,
касающихся до военной науки», изданная в 1 607 и 1621 годах и содержащая
некоторые геометрические сведения, которые сводятся к определенным приемам
решения задач на нахождение расстояний.
• Для измерения расстояния от точки Я до точки Б (см. рис. 1) рекомендуется вбить в точке Я жезл примерно в рост человека. К верхнему концу жезла Ц прилагается вершина прямого угла угольника так, чтобы один из катетов (или его продолжение) проходил через точку Б. Отмечается точка З пересечения другого катета (или его продолжения) с землей. Тогда расстояние БЯ относится к длине жезла ЦЯ так, как длина жезла к расстоянию ЯЗ. Для удобства расчетов и измерений жезл был разделен на 1000 равных частей.
• За шесть веков до нашей эры греческий мудрец Фалес Милетский вычислил высоту египетской пирамиды, измерив длину ее тени. Как это было, рассказывается в книге Я. И. Перельмана «Занимательная геометрия». Фалес, говорит предание, избрал день и час, когда длина собственной его тени равнялась его росту. В этот момент высота пирамиды должна также равняться длине отбрасываемой его тени. Вот, пожалуй, единственный случай, когда человек извлек пользу из своей тени.
ПРИТЧА
Усталый чужеземец пришел в страну Великого Хапи. Солнце уже садилось, когда он подошел к великолепному дворцу фараона. Он что-то сказал слугам. По мановению руки распахнулись перед ним двери и провели его в приемную залу. И вот он стоит в запыленном походном плаще, а перед ним на золоченом троне сидит фараон. Рядом стоят высокомерные жрецы, хранители великих тайн природы.
— Кто ты? — спросил верховный жрец.
— Зовут меня Фалес. Родом я из Милета.
Жрец надменно продолжал:
— Так это ты похвалялся, что сможешь измерить высоту пирамиды, не взбираясь на нее? — Жрецы согнулись от хохота.
— Будет хорошо, — насмешливо продолжал жрец, — если ты ошибешься не более чем на 1 00 локтей.
— Я могу измерить высоту пирамиды и ошибусь не более чем на пол-локтя. Я сделаю это завтра.
Лица жрецов потемнели. Какая наглость! Этот чужеземец утверждает, что может вычислить то, чего не могут они — жрецы великого Египта.
— Хорошо, — сказал фараон. — Около дворца стоит пирамида, мы знаем ее высоту. Завтра проверим твое искусство.
На следующий день Фалес нашел длинную палку, воткнул ее в землю чуть поодаль пирамиды. Дождался определенного момента. Провел некоторые измерения, сказал способ определения высоты пирамиды и назвал ее высоту.
Когда тень от палки будет той же длины, что и сама палка, то длина тени от центра основания пирамиды до ее вершины будет иметь ту же длину, что и сама пирамида. СЕ = Т), то есть Н = Ь.
Преимущества: не требуются вычисления.
НеДостатки: нельзя измерить высоту предмета при отсутствии солнца и, как следствие, тени.
У р о 42. Тема: ЗАДАЧИ НА ПОСТРОЕНИЕ МЕТОДОМ ПОДОБИЯ
|
Цель деятельности чителя |
Создать условия для применения подобия треугольников в задачах на построение |
|
|
Те мины и понятия |
П опо циональныео езки, отношение, п опо ции, с еднееп по циональное |
|
|
Плани емые ез льтаты |
||
|
П едметные мения |
Униве сальные чебные действия |
|
|
|
2 |
|
|
Владеют навыками устных, письменных, инструментальных вычислений |
Познавательные: умеют видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей хмзни. |
|
Продолжение табл.
|
|
1 |
2 |
|
|
|
Регулятивные: умеют адекватно оценивать правильность или ошибочность выполнения учебной задачи. Коммуникативные: учитывают разные мнейия и стремятся к координации различных позиций в сотрудничестве. Личностные: проявляют креативность мышления, инициативность, находчивость, активность при решении геометрических задач |
|
|
О ганизация п ост анства |
|
|
Фо мы аботы |
Ф онтальная Ф ; индивид альная И |
|
|
Образовательные ес сы |
• Учебник. • Задания для индивид альной аботы |
|
|
|
этап. Активизация знаний чащихся |
|
|
ель деятельности |
Совместная деятельность |
|
|
Выявить трудности, возникшие при выполнении домашнего задания |
I . Проверка домашнего задания. Разобрать задачи, с которыми не справилось большинство учащихся. 2. Заслушать сообщения учащихся о подобии в жизни человека. З. Решить задачи на построение: I ) Постройте медиану А]“ треугольника АВС 2) Постройте биссектрису МА треугольника МАК. З) Постройте высоту РК треугольника PST. 4) Пост ойте п ям ю, па аллельн ю сто онеАВт е гольника АВС и п оходящ ю че ез точк С |
|
|
|
II этап. Решение задач на пост оение методом подобия |
|
|
ель деятельности |
Совместная деятельность |
|
|
|
2 |
|
|
Научить решать задачи на построение методом подобия |
1 . Разобрать задачу № 584 (деление отрезка в данном отношении). Учащиеся самостоятельно читают решение задачи по учебнику, а затем один из наиболее подготовленных учеников решает ее у доски, остальные — в тетрадях. 2. Решить задачу ЛФ 585 (а) на доске и в тетрадях. Один из учащихся работает у доски, остальные — в тетрадях. Г,Г2 585 (а). Пл ан построения: 1) Построить луч AD и отложить на нем отрезки АК и kD так, чтобы АК : О = 2 : 5 (например, АК = 2 см, kD = 5 см). 2) Провести прямую BD. 3) Провести прямую К И BD (Е е АВ). AF : ЕВ = АК : kD=2 : 5. 3. Прочитать сдмостоятельно п. 66 (задачу З). 4. Решить самостоятельно задачу № 586 с последующим обсуждением. Учащиеся решают задачу в тетрадях, затем один из них по желанию выходит к доске и комменти ет свое ешение. |
|
Окончание
|
|
2 |
|
|
|
Построение: 1) Построить угол, равный данному (И). 2) Построить биссектрису данного угла и отложить на ней отрезок (АО), равный биссектрисе данного треугольника. 3) Построить угол, равный второму углу, (ZBI) от произвольной точки на одной из сторон первого угла. 4) Через точку О провести прямую, параллельную ОД 5) Прямая ОВ пересекается со второй стороной угла в точке С. ДАВС — искомый.
5. Решить самостоятельно задачу № 589.
Рис. 2 Построение (рис. б):
2) Построить отрезки АС1 и АД на сторонах И так, что АД а а З)
Откладываем отрезок АВ = 4) ЛАВС — искомый Рис. З |
|
|
III этап. Итоги |
ока. Ре лексия |
|
|
Деятельность чителя |
еятельность чащихся |
|
|
— Что оказалось сложным для вас в этом уроке? — Что необходимо сделать, чтобы минимизи овать т удности? |
(И) Домашнее задание: № 585 (б, в), 587, 588, 590 |
|
У рок 43. Тема: ЗАДАЧИ НА ПОСТРОЕНИЕ МЕТОДОМ ПОДОБИЯ
|
Цель деятельности чителя |
Создать условия для применения подобия треугольников в задачах на построение |
|
|
Те мины и понятия |
П опо циональные от езки, отношение, п опо ции, с еднее п опо циональное |
|
|
Плани емые ез льтаты |
||
|
П едметные мения |
Униве сальные чебные действия |
|
|
Владеют навыками устных, письменных, инструментальных вычислений, построений |
Познавательные: умеют видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни. Регулятивные: умеют адекватно оценивать правильность или ошибочность решения учебной задачи. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: проявляют креативность мышления, инициативность, находчивость, активность п и ешении геомет ических задач |
|
|
О ганизация п ост анства |
||
|
Фо мы аботы |
Ф онтальная Ф • индивид альная И пповая Г |
|
|
Образовательные ес сы |
• Учебник. • Задания для г пповой и индивид альной аботы |
|
|
этап. Активизация знаний чащихся |
||
|
ель деятельности |
Совместная деятельность |
|
|
Выявить трудности в выполнении домашнего задания |
1 . Проверка домашнего задания. Г•Г2 588. Дано: ZA = а, АМ= а (медиана), АВ : АС— 2 : 3 (рис. la).
а Рис. la Рис. 16 Построение (рис 16): 1) ZA а. 2)
Построить на сторонах И отрезки АД и ACl так, что АД : ACl 3) Отметить середину ВС] — точку К. АК — медиана МВБ. 4) На луче АК отложить отрезок АМ, равный а. 5 Че ез точк А п овести п ям ю ВС BlCl. ДАВС— искомый |
|
Продолжение
|
П этап. Решение задач |
||
|
Цель деятельности |
Совместная деятельность |
|
|
|
2 |
|
|
Совершенствовать навыки решения задач методом подобия |
(Г) Каждую из задач учащиеся решают самостоятельно в группах, а затем идет обсуждение решения, ного способа. I . Построить треугольник АВС по углу А, отношению сторон АВ : АС = 2 : I и расстоянию от до вершины С. Дано: И = а, О— точка пересечения медиан ДАВС, ОС = т, АВ : АС = 2 : 1. Построить: ЛАВС. Построение : а) Построить угол А, равный а. б) На сторонах угла А отложить отрезки АС1 и АД так, что ABi : ACl = 2 : 1. в) Построить точку пересечения медиан треугольника ABlCl — точку 01. г) На луче ОС] отложить отрезок ФЕ, равный т. д) Построить прямую ЕС, параллельную медиане АЛЛ треугольника ABiCl, С = ЕС П АСЬ
Рис. 2а Рис. 26 2. Построить отрезок а = п
В прямоугольном ДАВС Ш) — высота, проведенная из вершины прямого угла, поэтому BD — В» : О = : т, Л = CD-Ck. Если т, то л = : п- т. Построение: а) Построить МВД в котором ZD = 90 0 , BD = т, AD = п. |
выбор наиболее рациональ- точки пересечения медиан искомый.
|
Окончание
|
|
2 |
|
|
|
б) Провести прямую ВС так, что ВС -LAD = С. в) На луче СА отложить отрезок СК, равный т.
Рис. За Рис. 36 |
|
|
III этап. Самостоятельная абота |
||
|
Цель деятельности |
Задания для самостоятельной аботы |
|
|
Совершенствовать навыки решения задач методом подобия |
(И) Вариант 1 Постройте прямоугольный треугольник по острому углу и медиане, проведенной из вершины этого угла. Вариант П Пост ойте п ямо гольный т е гольник по ост ом гл и биссект исе п ямого гла |
|
|
IV этап. Итоги ока. Ре лексия |
||
|
Деятельность чителя |
Деятельность чащихся |
|
|
— Оцените свою работу на уроке. — Какой этап ока был наиболее сложным? |
(И) Домашнее задание: решить № 629 |
|
У р о к 44. Тема: СИНУС, КОСИНУС И ТАНГЕНС ОСТРОГО УГЛА ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА
|
Цель деятельности чителя |
Создать условия для введения понятий синуса, косинуса и тангенса острого угла прямоугольного треугольника и ознакомления чащихся с основным т игономет ическим тождеством, показать его п именение в п оцессе ешения задач |
|
|
Те мины и понятия |
Син с, косинус, тангенс, основное игономет ическое тождество |
|
|
Плани емые ез льтаты |
||
|
П едметные мения |
Униве сальные чебные действия |
|
|
Владеют геометрическим языком |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий. Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: проявляют креативность мышления, инициативность, находчивость, активность п и ешении геомет ических задач |
|
|
Цель деятельности чителя |
Создать условия для обучения учащихся вычислению значений синуса, косинуса и тангенса для углов 30 0 , 450 и 600 |
|
|
Те мины и понятия |
Синус, косин с, тангенс, основное т игономет ическое тождество |
|
|
Плани емые езультаты |
||
|
П едметные умения |
Униве сальные чебные действия |
|
|
|
2 |
|
|
Владеют геометрическим языком |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, становления аналогий. |
|
![]() Окончание
Окончание
|
О ганизация п ост анства |
|||
|
Фо мы аботы |
Ф онтальная (Ф); па |
ная (П); индивидуальная (И) |
|
|
Образовательные ес сы |
• Учебник. • Задания для па ной аботы |
||
|
этап. Активизация знаний чащихся |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Проверить правильность выполнения домашней аботы |
1. Сообщить результаты самостоятельной работы и прокомментировать допущенные ошибки. 2. П ове ить п авильность выполнения домашнего задания |
||
|
П этап. Из чение нового мате иала |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Ввести понятия синуса, косинуса, тангенса угла |
(Ф) 1 . Изложить в виде лекции содержание пункта 68. (П) 2. Творческая работа. Решить самостоятельно, обсуждая в парах, з ад а чу : Докажите, что если острый угол одного прямоугольного треугольника авен ос ом гл д угого п ямо гольного еугольника, то син сы этих углов авны и тангенсы этих глов авны |
||
|
III этап. Зак епление изученного мате нала |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Отработать введенные понятия на простых п име ах |
Работа у доски и в тетрадях. Выполнить № 591 (а, б), 592 (а, в, д), 593 (а) |
||
|
IV этап. Итоги |
ока. Ре лексия |
||
|
Деятельность чителя |
Деятельность учащихся |
||
|
— С какими понятиями познакомились на уроке? — Составьте синквейн к у ок |
(И) Домашнее задание: выучить определения синуса, косинуса, тангенса угла прямоугольного треугольника; решить № 591 (в, г), 592 (б, г, е), 539 (6 |
||
У р о к 45. Тема: ЗНАЧЕНИЯ СИНУСА, КОСИНУСА И ТАНГЕНСА ДЛЯ УГЛОВ 300 , 45 0 И 600
Продолжение
|
|
|
2 |
|
|
|
Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: креативность мышления, инициативность, находчивость, активность при решении геометрических задач |
|
|
Организация пространства |
|
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные ресурсы |
• Учебник. • Задания для индивидуальной работы |
|
|
|
этап. Активизация знаний учащихся |
|
|
цель деятельности |
Совместная деятельность |
|
|
Проверить уровень усвоения теоретического материала |
(Ф) 1. Проверка домашнего задания.
а Записать значения sina, cosa, tga для данных треугольников. 2. Катеты треугольника равны З см и 4 см. Чему равны синусы его острых углов? 3. Гипотенуза АВ прямоугольного треугольника равна 10 см, а катет ВС равен 8 см. Чему равны тангенсы его острых углов? (И) 4. Работа по карточкам. Карточка 1) В треугольнике ЛПК Zk= 90 0 , ДТ = 13 см, Nk= 5 см. Найдите синусы, косинусы и тангенсы углов Ми N. 2) Найдите cosa и tga, если sina = 0,3. Карточка №2. З 2 1) Постройте угол А, равный а, такой, что: а) sina = — • б) tga = 5 2) В равнобедренном треугольнике АВС (АВ = ВС) основание равно 12 см, а высота, проведенная к ней, 8 см. Найдите синусы, косинусы и тангенсы углов при основании |
|
Продолжение
|
II этап. Из чение нового мате иала |
||||||||||||||||||||
|
Цель деятельности |
Совместная деятельность |
|||||||||||||||||||
|
Научить находить значения синусов, косинусов и тангенсов для углов 300 , 45 0 , 600 |
(Ф) Используя текст учебника (п. 69) объяснить, как вычисляются значения синусов, косинусов и тангенсов для углов 30 0 , 45 600. В ходе объяснения на доске и в тетрадях заполнить таблицу:
|
|||||||||||||||||||
|
III этап. Зак епление из ченного мате иала |
||||||||||||||||||||
|
ель деятельности |
еятельность чителя |
|
еятельность чащихся |
|||||||||||||||||
|
|
2 |
|
3 |
|
||||||||||||||||
|
Формировать навыки решения прямоугольНЬЖ треугольников, используя синус, косинус и тангенс острого угла |
1. Решить № 593 (а) — для значения а= 30 0 ; № 593 (б) — для значения а = 45 0 (устно); № 601, 594 597, 598 (а). 2. Решить на доске и в тетради № 594. З. Решить № 597 |
Решение: АС 1) tgZB = — вс
sinp 2) Если Ь = 10
Ответ: • tgp |
дано: МВС, ZC = 900 , Выразить: ВС и И, АВ. Рис. 2 АС (по определению). ВС = tgZP см, 50 0 , то
ВС = 10 13,05 (см). 0,766 90 0 -д ; 8,39 см ; sinp |
= р, АС
8,39 (см); ZA = 400; 13,05 см |
||||||||||||||||
Окончание
|
|
2 |
|
З |
|
|
|
597.
Решение: 1 ) АВ2 = или tgZA 2) Если а = tgZA = Ц = 15 тельно, ZB |
в дано: МВС, ZC = 90 0 , ВС = а, АС Выразить: АС, ZA и ZB. а Рис. + ВС2 , АВ = а • tgZB = а 12
см, 15 см, то 15 0,8, следовательно, ZA 38 0 39', tgZB = = 1,25, следова12 51 021' |
|
IV этап. Итоги |
урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
||
|
Предложить дать рефлексивную оценку через выполнение определенных движений: присесть на корточки — очень низкая оценка, негативное отношение; — присесть, немного согнув ноги в коленях, — невысокая оценка, безразличное отношение; — обычная поза стоя, руки по швам — удовлетворительная оценка, спокойное отношение; — поднять руки в локтях — хорошая оценка, позитивное отношение; поднять руки вверх, хлопая в ладоши, подняться на носочки — очень высокая оценка, восторженное отношение |
(И) Домашнее задание: № 595, 596, 598 (б), 600; подготовиться к самостоятельной работе по S 3 |
||
У р о к 46. тема: СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА. РЕШЕНИЕ ЗАДАЧ
|
Цель деятельности чителя |
Создать условия для совершенствования навыков решения прямоугольных треугольников |
||
|
Те мины и понятия |
Син с, косин с, тангенс, основное т игономе ическое тождество |
||
|
Плани емые ез льтаты |
|||
|
П едметные мения |
Униве сальные чебные действия |
||
|
Владеют геометрическим языком |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий. Регулятивные: умеют адекватно оценивать правильность или ошибочность выполнения учебной задачи. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: проявляют способность к эмоциональному восприятию математических объктов, задач, ешений, асс ждений |
||
|
О ганизация п ост анства |
|||
|
Фо мы аботы |
Ф онтальная Ф ; индивид альная И |
||
|
Образовательные ес сы |
• Учебник. • Задания для индивид алычой аботы |
||
|
1 этап. Активизация опо ных знаний чащихся |
|||
|
ель деятельности |
Совместная деятельность |
||
|
Проверить уровень усвоения теоретического мате иапа |
(Ф/И) Проверка домашнего задания (см. Ресурсный материал) |
||
|
11 этап. Решение задач |
|||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
|
Совершенствовать навыки решения задач |
(Ф) Решить задачи № 601, № 602 у доски и в тетрадях |
|
|
|
III этап. Самостоятельная абота |
|||
|
ель деятельности |
Задания для самостоятельной аботы |
||
|
|
2 |
||
|
Проверить уровень сформированности навыков решения прямоугольных треугольников |
(И) Вариант 1 В равнобедренной трапеции меньшее основание равно 4 см, боковая сторона равна 6 см, а один из углов трапеции равен 120 0 . Найдите площадь трапеции. Вариант II В прямоугольной трапеции меньшее основание равно З см, ббльшая боковая сторона 4 см, а один из углов равен 150 0 . Найдите площадь т апеции. |
||
Окончание
|
|
|
||||||||||||||||||
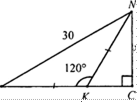
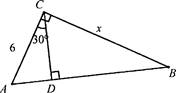
Ресурсный материал Домашнее задание Найдите х. в
![]() 4.
4.
м
8.
У к 47. Тема: ПОДГОТОВКА К КОНТРОЛЬНОЙ РАБОТЕ
|
Цель деятельности учителя |
Создать условия для совершенствования навыков решения прямоугольных треугольников, применения подобия |
|
|
Термины и понятия |
Синус, косинус, тангенс |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Владеют геометрическим языком |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий. Регулятивные: умеют адекватно оценивать правильность или ошибочность выполнения учебной задачи. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: проявляют способность к эмоциональному восприятию математических объктов, задач, решений, рассуждений |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные ресурсы |
• Учебник. • Задания для индивидуальной работы |
|
|
К этап. Активизация знаний учащихся |
||
|
Цель деятельности |
Совместная деятельность |
|
|
|
2 |
|
|
Подготовить учащихся к контрольной работе |
(И) Провести тест с целью повторения основных теоретических фактов с последующей самопроверкой. Вариант К в 1.
2. Для данного треугольника (рис. 1) справедливо равенство:
6) АВ -.AD = ВС : де,
|
|
Продолжение
|
|
2 |
||||
|
|
З. 4. а) б) в) 5. 6. 7. 8. а) |
В
Рис. 2 Треугольник, равносторонним; прямоугольным; равнобедренным. в
Рис. а Рис. 4
Рис. 5 Значение
|
D с выражения |
образованный с sin 60 C3+di 2 |
Для данного треугольника справедливо равенство: а) ВО : ОЕ= 1 : 2; 6) АО = -AD•, в) OD = 20. средними линиями прямоугольного треугольника, является: ПЛ — средняя линия треугольника АВС, если: а) в) Для данного треугольника справедливо равенство: а) а = Ь • cosa; б) а = с • cosa; в) а = с • sina. Для данного треугольника справедливо равенство: а) с = Ь • tga; 6) tgB•, в) Ь = с • tga. 0 + cos 45 0 равно: 4 |
[1роДолжение

Продолжение
|
|
2 |
|||||||||||||||||||||||||||||||||||||
|
|
а) а = Ь • tga; а б) а = Ь • tgB; в) Ь = а • tgB. Ь Рис. 5 8. Значение выражения sin 45 0 + cos 600 равно: а)
|
|||||||||||||||||||||||||||||||||||||
|
П этап. Решение задач по готовым че тежам |
||||||||||||||||||||||||||||||||||||||
|
ель деятельности |
Совместная деятельность |
|||||||||||||||||||||||||||||||||||||
|
Совершенствовать навыки решения задач |
(ФИ) 1. 2. Решить 1) 2) 4 к 3) 4) |
Проанализировать как можно больше промежуточные результаты
|
ошибки, допущенные в тесте. задач, записав в тетрадях краткое решение; на рисунке. Найти: ВС, АС S 5) Найти: мк, И. 6) дано: МЕ = Ь, ZMPE = р 7) Найти: мр и РА. Дано: BF — биссектриса. 8) Найти: ВЕ |
В А |
самые Рис. м 8 з к |
Рис.
|
простые с 6 м н Рис. |
задачи можно решить устно, записав Дано: ABCD — прямоугольник. Найти: СД АС, SABCD. дано: Ww: МК=5 : З, АС + ВС = 48. Найти: Мм, МК. дано: АВМН-прямоугольник. Найти: ВН. дано: ABCD -трапеция. Найти: SABCD. 8 |
||||||||||||||||||||||||||||||
|
Цель деятельности чителя |
Создать условия для проверки знаний, умений и навыков учащихся по усвоению и применению изученного материала |
|
|
Те мины и понятия |
Син с, косин с тангенс |
|
|
Плани емые ез льтаты |
||
|
П едметные мения |
Униве сальные чебные действия |
|
|
Умеют демонстрировать знание основных понятий, применять полученные знания для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности |
Познавательные: умеют проводить сравнение, сериацию и классификацию по заданным критериям. Регулятивные: вносят необходимые коррективы в действие после его завершения на основе его учета характера сделанных ошибок; осуществляют самоанализ и самоконтроль. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: осознают важность и необходимость знаний для человека |
|
|
О ганизация п ост анства |
||
|
Фо мы аботы |
Индивид альная И |
|
|
Образовательные ес сы |
• Учебник. • Задания для индиви альной аботы |
|
|
этап. Выполнение конт ольной аботы |
||
|
цель деятельности |
Задания для кон ольной аботы |
|
|
|
2 |
|
|
Проверить знания, умения, навыки по изученному материалу |
(И) Вариант 1 1. В прямоугольном треугольнике АВС И = 900 , АВ = 20 см; высота AD = 12 см. Найдите АС и cosZC. 2. Диагональ BD параллелограмма ABCD перпендикулярна стороне AD. Найдите площадь параллелограмма ABCD, если 12 см, U = 41 0 . |
|
Окончание
|
|
2 |
|
|
|
Найти: сиг.СЕ + ВР + АК = 21. Найти: СЕ, виг, АК. Рис. 9Рис. 10 |
|
|
III этап. Итоги ока. Ре лексия |
||
|
еятельность чителя |
еятельность чащихся |
|
|
— Оцените свою работу, работу своего соседа по парте. — Оцените степень готовности к конт ольной аботе |
(И) Домашнее задание: задачи, которые не успели сделать в классе |
|
У рок 48. Тема: КОНТРОЛЬНАЯ РАБОТА 4
|
|
2 |
|
|
|
Вариант П I . Высота BD прямоугольного треугольника АВС равна 24 см и отсекает от гипотенузы АС отрезок DC, равный 1 8 см. Найдите АВ и cosZA. 2. Диагональ АС прямоугольника ABCD равна З см и составляет со стороной AD угол 37 0 . Найдите площадь прямоугольника АВСД В а р и а нт III (для более подготовленных учащихся) I. Диагональ АС равнобедренной трапеции ABCD перпендикулярна боковой стороне CD. Найдите площадь трапеции, если ее основания равны 10 см и 8 см. 2. Найдите отношение высот BN и АМ равнобедренного треугольника АВС, в котором угол при основании ВС равен а |
|
|
П этап. Итоги урока |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
|
(И) Домашнее задание: повторить п. 21 «Окружность», п. 38 |
|
|
Цель деятельности учителя |
Создать условия для рассмотрения различных случаев взаимного расположения прямой и окружности |
|
|
Термины и понятия |
Окружность, хорда, радиус, диаметр, касательная |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Владеют базовым понятийным аппаратом по основным разделам содержания |
Познавательные: умеют устанавливать причинно-следственные связи, строить логическое рассуждение, делать умозаключения и выводы. Регулятивные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических задач. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: имеют целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И); групповая (Г) |
|
|
Образовательные ресурсы |
• Учебник. • Задания для фронтальной, групповой работы |
|
ГЛАВА VIII. ОКРУЖНОСТЬ
У рок 49. Тема: ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И
ОКРУЖНОСТИ
•ПроДолжение
|
этап. Актуализация знаний учащихся |
|
|
|
Цель деятельности |
Совместная деятельность |
|
|
Подвести итог контрольной работы, решить задачи, подготавливающие к изучению новой темы |
(Ф) 1. Анализ контрольной работы. 2. Решение задач (устно). Вспомнить, что такое окружность, ее элементы. 1. Радиус окружности 5 см. Найдите расстояние от центра окружности до прямой, содержащей хорду, равную 8 см.
2. Найдите расстояние от точки А до ближайшей к ней точки окружности с центром О радиуса r, если: а) ОА — 12 см, б) АО 6 см, r 8 см. а) Рис. 2 Рис. З AB=OA-r,
З. Докажите, что АВ < АД, используя неравенство треугольника. имеем т <0Bl + Щ, ОВ+АВ < ОЩ + АД, так как ОВ= ОЩ — r, то АВ < АВ.
Рис. 4 |
8 см; |
|
П этап. Учебно-познавательная деятельность |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Выяснить, от чего зависит взаимное расположение прямой и окружности |
(Ф/ГШ) Задача. Даны окружность радиуса r и прямая р, не проходящая через центр О окружности. Расстояние от точки О до прямой р равно d. Сколько точек пересечения могут иметь данные окружность и прямая, если: а) d < r; б) d= r; в) d> к? Для решения данной задачи класс можно разбить на творческие группы по 3—4 ученика в каждй, у каждой группы — свое задание (рассмотреть один из случаев по указанию учителя). Проводится обсуждение решения задачи. В ходе обсуждения на доске необходимо выполнить рис. 21 (а, б, в) из учебника на с. 163 и записать краткое решение задачи |
||
|
III этап. Закрепление изученного материала |
|||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
|
На простых задачах отработать взаимное расположение прямой и окружности |
(Ф) Решить № 631 (а, г, д) (устно), 632
|
Дано: окружность (О; r), ОА =d, ОВ = r, d < r,A Е l. Доказать: I — секущая. Рис. 5 Доказательство: 1) Если I д- Ш, то d < r и по определению I — секущая. 2) Если I не 0,4, то ОК -L I и прямоугольный ОА — гипотенуза, значит ОА > ОК. Так как по условию r > 0,4, r > ОК, значит I — секущая по определению |
|
|
IV этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
— Что нового узнали на уроке? — Каково взаимное расположение прямой и окружности? — Составьте синквейн к уроку |
(И) Домашнее задание: вопросы 1, 2, с. 184; № 631 (б, в), 633; выполнить работу над ошибками, допущенными в контрольной работе |
||
У к 50. Тема: КАСАТЕЛЬНАЯ К ОКРУЖНОСТИ
|
Цель деятельности чителя |
Создать условия для введения определения касательной к окружности, рассмотрения свойства касательной и свойства отрезков касательных, п оведенных из одной точки |
|
|
Те мины и понятия |
Ок жность, хо да, ади с, диамет , касательная |
|
|
Плани емые ез льтаты |
||
|
П едметные мения |
Униве сальные чебные действия |
|
|
Владеют базовым понятийным аппаратом по основным разделам содержания |
Познавательные: умеют устанавливать причинно-следственные связи, строить логическое рассуждение, делать умозаключения и выводы. Регулятивные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических задач. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: имеют целостное мировоззрение, соответствующее современному уровню азвития на ки и общественной п актики |
|
|
О ганизация п ост анства |
||
|
Фо мы аботы |
Ф онтальная Ф ; индивид альная И |
|
|
Образовательные ес сы |
• Учебник. • Задания для индивид альной аботы |
|
|
этап. Ак ализация знаний чащихся |
||
|
ель деятельности |
Совместная деятельность |
|
|
Выявить трудности, возникшие при выполнении домашнего задания |
(Ф) 1. Прокомментировать номера, в которых у учащихся возникли трудности. 2. Провести тест с целью проверки теории (на листочках). 1) Среди следующих утверждений укажите истинные. Окружность и прямая имеют две общие точки, если: а) расстояние от центра окружности до прямой не превосходит радиуса окружности; б) расстояние от центра окружности до прямой меньше радиуса окружности; в) расстояние от окружности до прямой меньше радиуса. 2) Закончите фразу, чтобы получилось верное высказывание. Окружность и прямая имеют одну общую точку, если... З) Вставьте пропущенные слова. Окружность и прямая имеют одну общую точку, если ... расстояние от ... до прямой ... 4) Установите истинность или ложность следующих утверждений: а) Прямая а является секущей по отношению к окружности, если она имеет с окружностью общие точки. б) Прямая а является секущей по отношению к окружности, если она пересекает окружность в двух точках. в) Прямая а является секущей по отношению к окружности, если расстояние от центра окружности до данной прямой не больше ади са |
|
|
П этап. Учебно-познавательная деятельность |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Ввести понятие касательной к окружности и доказать сопутствующие теоремы |
(Ф) 1. Ввести понятие касательной и точки касания. 2. Свойство касательной к окружности. (Доказывают учащиеся самостоятельно.) З. Свойство отрезков касательных, проведенных из одной точки. (Доказывают учащиеся самостоятельно.) |
||
|
этап. Решение задач на закрепление |
|||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
|
На простых задачах отработать понятия касательной и точки касания |
Решить № 635 (устно), 639, 646, 636, 645. Решить дополнительную задачу: АВ и ВС — отрезки касательных, проведенных из точки В к окружности с центром О. Найдите АВ и ВС, если ОА = 16 см, а радиусы, проведенные к точкам касания, взаимно перпендикулярны |
в Так как ВА и ВС — отрезки касательных, проведенных из одной точки к окружности, то ОА АД ОС СВ, АВ = ВС и Zl = П, значит, ИОВ = СОВ. Так Т ОСИ ИОВ = СОВ = 45 0 Д = 45 0 , П = 45 0 . МОВ — равнобедренный с основанием ОД значит, ОА =АВ. По теореме Пифагора 0,4 2 + АВ2 = ОВ2 гэ так как ОА = АД то 20А 2 = 162 ОА = см АВ = ВС = см. Ответ: см, см |
|
|
IV этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
— Какие новые понятия узнали на уроке? — Какой этап урока оказался наиболее сложным? |
(И) Домашнее задание: вопросы 3—7, с. 1 84; № 634, 638, 640; самостоятельно доказать признак касательной |
||
|
Цель деятельности учителя |
Создать условия для совершенствования навыков решения задач по теме |
|
|
Термины и понятия |
Окружность, хорда, радиус, диаметр, касательная |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Владеют базовым понятийным аппаратом по основным разделам содержания |
Познавательные: понимают и используют математические средства наглядности. Регулятивные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических задач. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные ресурсы |
• Учебник. • Задания для индивидуальной работы |
|
|
этап. Проверка домашнего задания |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Проверить уровень усвоения теоретического материала |
(Ф) 1. Привести доказательство признака касательной к окружности. (Заслушать одного ученика.) 2. Проверить выполнение домашнего задания и ответить на вопросы учащихся |
|
|
этап. Самостоятельная работа |
||
|
Цель деятельности |
Задания для самостоятельной работы |
|
|
Совершенствовать навыки решения задач по теме |
(И) Учащиеся решают самостоятельную работу на листочках и сдают учителю на проверку. Вариант 1 1. КМ и ЮМ— отрезки касательных, проведенных из точки К к окружности с центром О. Найдите КМ и Т, если ОК = 12 см, ZMON= 120 0 . 2. Диагонали ромба ABCD пересекаются в точке О. Докажите, что прямая BD касается окружности с центром А и радиусом, равным ОС. Вариант 1. Найдите отрезки касательных АВ и АС, проведенных из точки А к окружности радиуса r, если = 9 см, ZBAC = 120 0 . 2. В равнобедренном треугольнике АВС с основанием АС проведена медиана BD. Докажите, что прямая BD касается окружности с центром С и радиусом, равным AD |
|
Продолжение
|
Ш этап. Решение задач |
|
|||
|
Цель деятельности |
Деятельность учителя |
|
Деятельность учащихся |
|
|
|
2 |
|
|
|
|
Совершенствовать навыки решения задач по теме |
1. Решение задач по 1) 2)
Рис. З 4) |
готовым чертежам. Дано: R = 5, АВ — касательная. Найти: ОВ. Дано: АВ — касательная; АВ = 12
Найти: R окружности. Дано: АД ВС — касательные, ОВ = 2
Найти: пОС. Дано: АВ касательная, R = 6 АО = ОВ. Найти: АО. |
Ответ ы :
3) иос = 1200 . 4) АО = 10. |
|
Продолжение
|
|
2
Найти: Р с Рис. 5
Найти: ОС. Рис б 2. Решение задач из учебника (№ 647) |
З |
|
|
5) РАЖ 34. 6) ос = 6,25.
Найти: является ли АН касательной? Рис. 7 а) Если ОА = 5 см, АН = 4 см. Рассмотрим МНО ОА = 5, АН = 4, оН= З. 5 2 = 42 + 3 2 ; 25 = 25, значит, ДАНО — прямоугольный, ZOHA = 90 0 , следовательно, АН — касательная. 6) Если ZHAO= 45 0 , = 4 см. Рассмотрим МЮ: ОН = З, ОА = 4, ZHAO = 45 0 . Если предположить, что ZH = 90 0 , то АН = ОН = 3, следовательно, АО = 30 , что противоречит условию АО = 4, значит, предположение неверно, тогда АН не является касательной. в) Если ZHAO= 300 , ОА = 6 см. Рассмотрим МНО ОА = 6, он= З, И = 300 . Так как ОН— Т, следовательно, ZII = 90 0 , а значит АН — касательная окружности |
Окончание
|
|
IV этап. Итоги |
ока. Ре лексия |
|
еятельность чителя |
|
еятельность чащихся |
|
(Ф) Что сегодня повторили на уроке? Какие задачи вызвали у вас затруднения? Почему? |
|
(И) Домашнее задание: № 648; решить задачу (по желанию): Две окружности разных диаметров внешне касаются. К ним проведены две общие касательные АС и ВД где А и В — точки касания с первой окружностью, а С и D — со второй. Докажите, что АСЛ — равнобокая апеция |
У р о к 52. Тема: ГРАДУСНАЯ МЕРА ДУГИ ОКРУЖНОСТИ
|
Цель деятельности чителя |
Создать условия для введения понятий градусной меры дуги окружности, центрального угла |
|
|
Те мины и понятия |
Ок жность, хо да, ади с диаме га, хо да, стягивающая д г ок жности, цент альный гол |
|
|
Плани емые ез льтаты |
||
|
П едметные мения |
Униве сальные чебные действия |
|
|
Владеют базовым понятийным аппаратом по основным разделам содержания |
Познавательные: умеют понимать и использовать математические средства наглядности. Регулятивные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических задач. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками, работать в группах. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, ешений, асс ждений |
|
|
О ганизация п ост анства |
||
|
Фо мы аботы |
Ф онтальная Ф ; индивид альная И ; пповая Г |
|
|
Образовательные ес сы |
• Учебник. • Задания для онтальной и индивид альной аботы |
|
|
этап. Ак ализация оно ных знаний чащихся |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Провести общий анализ ошибок в самостоятельной работе и домашней аботе |
(Ф) 1. Анализ самостоятельной работы. 2. Проверка домашнего задания |
|
|
II этап. Из чение нового мате нала |
||
|
Цель деятельности |
Совместная деятельность |
|
|
|
2 |
|
|
Ввести понятие граДУСНОЙ меры дуги ок жности |
(Ф) 1. Ввести понятие дуги окружности, используя рис. 214 учебника. Ознакомить со способами обозначения дуг. 2. Ввести понятие пол ок жности, использ я ис. 215 а чебника. |
|
Окончание
|
|
2 |
||
|
|
3. Ввести понятие центрального угла, используя рисунок, и градусной меры дуги окружности.
иАСВ больше полуокружности гэ vACB = 3600 — ИОВ. Рис. 1 ШВ + = 360 |
||
|
III этап. Зак епление из ченного мате нала |
|||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
|
Научить решать простейшие задачи на вычисление градусной меры дуги окружности |
(ФМ), (Г) l. Решить задачи № 650 (а, в), 651 (устно). 2. Решить задачу № 649 (а, в) (самостоятельно). 3. Решить задачи № 715 и 716 в группах, затем показать свои решения |
га 649. а)
Рис. 5 |
Рис. З хорда. ИОВ = 120 0 , АВ - хорда. I. vAB = ИОВ, так как vAB меньше полуокружности. 2. vABl = ИОД, так как vABl мењше полуокружности. 3. ЛОВК = ДОВIК по гипотенузе и катету (ОВ = 0Bl как радиусы, ОК— общий катет, ОКВ = ZOkBl = = 900 ) ООК= цок = ИОВ =180 0 - ZB0k=
= - цок = ZAOB1 КИАВ = vCD
|
|
kV этап. Итоги рока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность чащихся |
||
|
— Какие новые понятия вы для себя открыли? — Составьте синквейн к уроку |
(И) Домашнее задание: вопросы 8, 9, 10, с. 184; № 650 (б), 652, 649 (б, г) |
||
|
Цель деятельности учителя |
Создать условия для введения понятия вписанного угла и рассмотрения теоремы о вписанном угле |
|
|
Термины и понятия |
Окружность, хорда, радиус, диаметр, дуга; хорда, стягивающая дугу окружности; вписанный угол |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Владеют базовым понятийным аппаратом по основным разделам содержания |
Познавательные: умеют создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных задач. Регулятивные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических задач. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками, работать в группах. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); парная (П); индивидуальная (И); групповая (Г) |
|
|
Образовательные ресурсы |
• Учебник. • Задания для индивидуальной работы |
|
|
1 этап. Актуализация опорных знаний учащихся |
||
|
Цель деятельности |
Совместная деятельность |
|
|
|
2 |
|
|
На простых задачах проверить уровень усвоения теоретического материала |
1 . Повторение теоретического материала в процессе решения задач на готовых чертежах (устно). 1)Дано: ОМКЕ в два раза меньше vMNE. Найти: ОМКЕ, vMNE.
ответ: ОМКЕ = 120 0 , ОМЛЕ =240 0 . к Рис.
Найти:
ИРЕ. ответ: vAPE=250 Рис. 2 |
|
Продолжение
2 дано: (ЛВ : ОВС : : З : 4. Найти: ИОВ, лОС, ДОС.
ответ: ИОВ 80 0 , ЛОС = 120 0 , ДОС = 1600 .
Рис. З
4) дано: ZMON : ZNOk: ZMOE= З : 4 : 5. Найти: ОМЕ, vNk, ОКЕ.
Ответ: ОМЕ = 120 0 , uNk= 96 0 , ОКЕ = 720 .
Рис. 4
Е к
2. Проверить домашнюю задачу № 652.
дано: АС = 37 0 , = 230 , R = 15 см. Найти: СД
О
Рис. 5 Решение.
60 0 = 120 0 .
2) В ДСО: ZO= 120 0 , ОС = О = 15 см. OEL СД sinZEOD= OD • sinZEOD•, 15 • sinZ600 = 15 — (см);
OD 2
CD=2 156 (см)
П этап. Учебно-познавательная деятельность
|
ель деятельности |
Задания для самостоятельной аботы 2 |
|
Подготовить уча- |
(ФИ). |
|
щихся к восприятию |
Решение задач на готовых чертежах (самостоятельно с последующим обсуждением). |
|
нового материала |
1. Найти: vAC. |
н
15
370
Рис. 6 Ответ: vAC = 600 .
|
|
2 |
||
|
|
Рис. 7 Ответ: ZABC = 45 |
||
|
111 этап. Изучение нового материала |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Ввести понятие вписанного угла и доказать сопутствующую теорему |
Рис. 9 а) Случай, когда луч ВО совпадает с одной из сторон угла АВС, учитель доказывает сам в ходе беседы с учащимися. б) Случаи, когда луч ВО делит угол АВС на два угла и когда луч ВО не делит угол АВС на два угла и не совпадает со стороной этого угла, учащимся предлагается доказать самостоятельно по вариантам с последующим обсуждением доказательств. Теорема. Вписанный угол измеряется половиной дуги, на которую он опирается |
||
|
IV этап. Закрепление изученного материала |
|||
|
Цель деятельности |
Деятельность учителя |
|
Деятельность учащихся |
|
|
2 |
|
|
|
Показать применение теоремы о вписанном угле и следствий при решении задач |
Задачи можно решать у доски. Выполнить № 653 (устно), 654 (устно), 655, 656 658, 659 (устно), 661 |
а) Решение. ZBAC= -ВС•, |
дано: Найти: ПАС. Рис. П 360 5 0 — 2020. Значит, ZBAC= 101 |
![]() Окончание
Окончание
|
|
2 |
З |
|
|
|
2 ПАС = 36 0 Рис. 12 Ответ: 101 0 или 36 0 .
Дано: АВ — касательная, AD — секущая, D окр (0, Ю, 100 20'. Найти: ZBAD, ПАВ. Рис. В Решение:
2 2) дтк -прямоугольный, так как ZDBk= —Dk = 900 . Значит, ОВА = 900 - ZBkD•, ZBDA = 89 0 60' - 55 0 10' = 340 50'. З) ДВП — равнобедренный, так как ОВ = 0D = R. Значит, ОВО = = ZBDO = 34 0 50',
отсюда ОВА = оВО + ZOBA = 34 0 50' + 900 = 1240 50'.
4) ZBAD = - ответ: 20 020' и 34 0 50' |
|
V этап. Итоги ока. Ре лексия |
||
|
Деятельность чителя |
Деятельность чащихся |
|
|
— Сформулируйте 3 вопроса по теме. Для того чтобы закончить урок на положительной ноте, можно воспользоваться одним из вариантов упражнения «Комплимент» («Комплиментпохвала», «Комплимент деловым качествам», «Комплимент в чувствах»), в котором учащиеся оценивают вклад друг друга в урок и благодарят друг друга и учителя за проведенное занятие. Такой вариант окончания урока дает возможность удовлетворения потребности каждого в признании личностной значимости |
(И) Домашнее задание: вопросы 1 1, 12, 13, с. 184; № 657, 660, 663; повторить I признак подобия треугольников; № 662, 664 (по желанию) |
|
У рок 54. Тема: ТЕОРЕМА ОБ ОТРЕЗКАХ ПЕРЕСЕКАЮЩИХСЯ ХОРД
|
Цель деятельности чителя |
Создать условия для рассмотрения теоремы об отрезках пересекающихся хорд и применения изученного материала при решении задач |
|
|
Те мины и понятия |
Ок жность, хо да, ад с, диамет га; хо да, стягивающая д г ок жности; вписанный гол |
|
|
Плани емые ез льтаты |
||
|
П едметные мения |
Униве сальные чебные действия |
|
|
Владеют базовым понятийным аппаратом по основным разделам содержания |
Познавательные: умеют создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных задач. Регулятивные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических задач. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками, работать в группах. Личностные: проявляют способность к эмоцрщнальному восприятию математических объектов, задач, ешений, асс ждений |
|
|
О ганизация п ост анства |
||
|
Фо мы аботы |
Ф онтальная Ф ; индивид альная И |
|
|
Образовательные ес сы |
• Учебник. • Задания для индивид альной аботы |
|
|
этап. Ак ализация опо ных знаний чащихся |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Повторить теоретический материал и выявить трудности, возникшие при выполнении домашнего задания |
|
|
|
П этап. Мотивация к деятельности |
||
|
Цель деятельности |
Постановка чебной задачи |
|
|
Подготовить учащихся к восприятию нового материала |
(Ф/И) Решить задачу.
Найти: АЕ, если 4 см; = 6 см, СЕ = 2 см Рис. 5 |
|
Продолжение
|
III этап. Изучение нового материала |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Вывести доказательство теоремы об отрезках пересекающихся хорд |
Доказательство теоремы об отрезках пересекающихся хорд можно провести в виде з ад а ч и : Докажите, что если две хорды АВ и CD окружности пересекаются в точке Е, то АЕ • ВЕ = СЕ • DE. Предложить решить задачу самостоятельно, а затем обсудить ее решение. В тетрадях и на доске записать план-конспект доказательства теоремы |
|
|
IV этап. Закрепление изученного материала |
||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
Совершенствовать навыки решения задач на применение теоремы о вписанном угле и ее следствий |
Решить № 666 (а; 6), 668, 670, 671 (а), 673. У доски можно выполнить № 668, 670 |
Дано: АВ — диаметр, CD Ш АД CD п АВ = К СТП. D Доказательство: 1) Так как CD АД по аналогичным рассуждениям в предыдущей задаче ск = КД 2) По свойству хорд: АК • КВ = СК • КД так как СК = КД то АК • КВ = Ck2 ; СК = АК • КВ , что и требовалось доказать.
Доказательство: Рассмотрим ЛАВР и MQB: ZA — общий, ZB = Z Q. ЛАВР MQB АВ АР (по двум углам), следовательно, По свойству пропорции, AQ АВ АВ2 = АР • AQ, что и требовалось доказать |
|
Цель деятельности чителя |
Создать условия для систематизации теоретических знаний по теме «Центральные и вписанные углы» |
|
|
Те мины и понятия |
Ок жность, хо да, ади с, диамет , д га; хо да, стягивающая д г ок жности; вписанный гол |
|
|
Плани емые ез льтаты |
||
|
П едметные мения |
Униве сальные чебные действия |
|
|
Умеют работать с геометрическим текстом, точно и грамотно излагать свои мысли в устной и письменной речи |
Познавательные: умеют создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных задач. Регулятивные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических задач. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками, работать в группах. Личностные: проявляют креативность мышления, инициативность, находчивость, активность п и ешении геомет ических задач |
|
|
О ганизация п ост анства |
||
|
Фо мы аботы |
Ф онтальная Ф ; индивид альная (И) |
|
|
Образовательные ес сы |
• Учебник. • Задания для индивид альной аботы |
|
|
V этап. Итоги урока. Рефлексия |
|
|
Деятельность учителя |
Деятельностк учащихся |
|
С какой теоремой познакомились на уроке? — Закончите фразу: • Было трудно.. • Я выполнял задания... • Я понял, что... • Теперь я могу... • Я почувствовал, что... • Я приобрел. . . • Я научился.. • У меня получилось. • Я смог... • Я поп об ю... |
(И) Домашнее задание: вопросы 1—14, с. 187; № 666 (б), 667, 671 |
У р о к 55. Тема: РЕШЕНИЕ ЗАДАЧ ПО ТЕМЕ «ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ»
ПроДолжение
|
этап. Актуализация опорных знаний учащихся |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Проверить правильность выполнения домашнего задания |
(ФМ) К доске вызываются 2 ученика: первый готовит доказательство теоремы; второй — решение задачи № 667. Дано: АИ — диаметр, АА] Ш ВЦ, АЛ п ВД = О, АС = 4 см, СА1 = 8 см. Найти: Щ.
Решение: 1) Так как АЛ Ш ВЦ, то ОС является высотой равнобедренного ДВОВ|, а значит, ОС — медиана, то есть ВС = СВ 2) По свойству хорд: АС • СА] = ВС • СА; 4 • 8 = х • х; х2 = 32, х = , ВС = . Отсюда ВВ1 = |
|
|
П этап. Решение задач |
||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
|
2 |
3 |
|
Совершенствовать навыки решения задач |
1. Решить задачу № 669. 2.
Решить задачи по готовым чертежам. Найти: ВЕ и а. Рис. 2 |
Построить отрезок АВ = ММ РК . Построение: а) на прямой построить отрезок АД равный сумме длин отрезков и РК; б) построить середину отрезка АВ — точку О; в) построить окружность с центром в точке О и радиусом, равным АО; г) построить перпендикуляр к отрезку АВ через точку Q, лежащую на отрезке АВ так, что AQ = MN, BQ = РК; д) построить точку пересечения данного перпендикуляра с построенной окружностью — точку Е; отрезок QE — искомый. 2. После решения задачи обратить внимание: угол, вершина которого лежит внутри круга, измеряется полусуммой двух дуг, одна из которых заюлючена между его сторонами, а другая — между продолжениями сторон. 1 а = — (vAB + UCD) 2 |
Продолжение
|
|
2 |
|
|
|
Рис.
Рис. 5 |
З. После решения задачи обратить внимание: угол, вершина которого лежит вне круга, измеряется полуразностью двух дуг, заключенных между его сторонами. а (vPQ - vNk). 2 4. Решение. 360 0 : 18 = 20 0 иАС=З 20 0 - 60 0 ; ИВ = 7 20 0 = 140 0 , ОСВ - 8 • 20 0 = 160 0 , значит, д = 30 0 , = 80 0 , Z3 = 70 0 . 5. Окружность проходит через вершины В, С, D трапеции ABCD (AD и ВС — основания) и касается стороны АВ в точке В. Докажите, что BD = ВС • AD Решение: 1) Так как ВС АД то Zl = Z2. 2) —uBED, —vBED, значит, Z3 = д. 3)
ДАО ВС |
|
этап. Самостоятельная абота |
||
|
ель деятельности |
Задания для самостоятельной аботы |
|
|
Совершенствовать навыки самостоятельной работы, самопроверки и самоконтроля |
1.дано: ШВ : иАС=З : 2, И = 50 0 . Найти: Л, ZC, ПОС. С Рис. 6 2. Хорды АВ и CD пересекаются в точке Е. Найдите СД если АЕ = 4 см, ВЕ — 9 см, а длина СЕ в четыре раза больше длины DE. Вариант П 1.дано: о = 60 0 , иАВ : ос = 7 : 5. Найти: И, С, ДОС. Рис. 7
|
|
Окончание
|
|
IV этап. Итоги урока. Рефлексия |
|
|
Деятельность учителя |
|
Деятельность учащихся |
|
— Оцените свою работу на уроке |
|
(И) Домашнее задание: № 661, 663 |
У 56. Тема: СВОЙСТВО БИССЕКТРИСЫ УГЛА
|
Цель деятельности учителя |
Создать условия для рассмотрения свойства биссектрисы угла и показать его применение при решении задач |
|
|
Термины и понятия |
Угол, биссектриса угла, равноудаленность |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Имеют систематические знания о плоских фигурах и их свойствах |
Познавательные: умеют создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных задач; применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач. Регулятивные: принимают и сохраняют учебные задачи. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют креативность мышления, инициативность, находчивость, активность при решении геометрических задач |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные ресурсы |
• Учебник. • Задания для индивидуальной работы |
|
|
этап. Актуализация опорных знаний учащихся |
||
|
Цель деятельности |
Совместная деятельность |
|
|
|
2 |
|
|
Составить план решения тех задач, с которыми учащиеся не справились в самостоятельной работе |
(ф) . Анализ ошибок, допущенных в самостоятельной работе. I ) Сообщить общие замечания и рекомендации по решению задач самостоятельной работы. 2) Составить план решения задач, с которыми не справилось большинство учащихся. 2. Проверка выполнения домашнего задания (№ 661, 663). |
|
Продолжение
|
|
2 |
|
|||
|
|
Дано: АС, ЕС — секущие, AF = Ш) = 52 0 . Найти: ИСТ.
1) ИВЕ-вписанный, значит, ZABF= —AF, ZABF= 70 0 . 2) ZBFD -вписанный, значит, ZBFD = — вд ZBFD = 26 0 . 3) в ДВст: 26 0 , о = - 70 0 - (как смежный с ИВЕ), ZC= - (110 0 + 26 0 ) = 44 0 . Ответ: 44 0 .
663. м дано: АС-диаметр, Окр (О; R), АВ — хорда, АЛЛ— касательная, ДИАВ < 90 0 . Доказать: ZMAB = ИСВ. Рис. 2 Доказательство:
1) ЛАВС — прямоугольный, так как ZB —- — АС = 90 0 , - ZBAC С). 2 2) Так как АМ— касательная к окружности, то АМ Ш АС, то есть ZMAB = 90 - ZBAC 3) Сравним ( * ) и (**), получим: ZC = ЛИВ, что и требовалось доказать |
|
|||
|
П этап. Мотивация к деятельности |
|
|
|||
|
Цель деятельности |
Постановка чебной задачи |
|
|
||
|
Совершенствовать навык решения задач по готовым чертежам с целью подготовки учащихся к восприятию нового мате иала |
2. Доказать: точка М равноудалена от точек А и В (рис. 4). З. Доказать: АС — биссектриса ZBAD (рис. 5)с D Рис |
в З Рис. 4 |
D Рис. 5 |
||
Продолжение
|
этап. Изучение нового материала |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Рассмотреть теорему о свойстве биссектрисы угла и ее следствие |
(Ф) . Доказательство теоремы. 2. Доказательство следствия из теоремы. Изложить доказательства лучше самому учителю в виде небольшой лекции |
|
|
IV этап. Закрепление изученного материала |
||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
|
2 |
3 |
|
Совершенствовать навыки решения задач |
Решить № 674, 675, 676 (а) |
Дано: ZO, ОМ— биссектриса, МА Ш ОА, мв ов. Доказать: АВ Ш ОМ. Доказательство: Рис. б 1 ) Рассмотрим ЛМОВ и ДМОА: ОМ— общая, Zl = 7.2 (по условию), следовательно, ДМОВ = ДМОА (по гипотенузе и острому углу). Значит, ОВ = 04, следовательно, МОВ — равнобедренный. 2) Рассмотрим ЛОВК и ЛОАК: ОВ = ОА (из п. 1), Zl = Z2 (по условию), ОК — общая, следовательно, ЛОВК = ДОАК (по двум сторонам и углу между ними), следовательно, ВК = КА, значит, ОК — медиана, тогда ОК Ш ВА (свойство медианы равнобедренного треугольника), что и требовалось доказать.
Доказать: 01, 02 Е ОА. Доказательство: 1) Так как ВС и BlCl — касательные к окружностям, то ав вс, ос вс и од вс, 02Cl BlCl. Значит, точки (А и 02 лежат на биссектрисе ZO — свойство биссектрисы угла. 2) А лежит на биссектрисе, так как АК = АК] (свойство биссектрисы), что и т ебовалось доказать. |
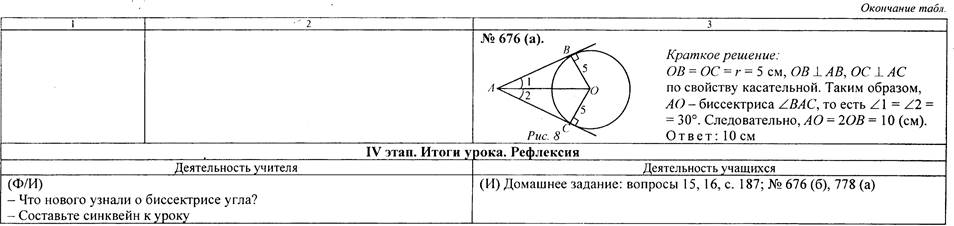
У рок 57. Тема: СЕРЕДИННЫЙ ПЕРПЕНДИКУЛЯР
|
Цель деятельности ч еля |
Создать условия для введения понятия серединного перпендикуляра и рассмотрения теоремы о серединном перпендикуляре; показать п именение тео емы о се единном пе пендик ля е п и ешении задач |
||
|
Те мины и понятия |
Се единный пе пендик ля авно даленность |
||
|
Плани емые ез льтаты |
|||
|
П едметные нения |
Униве сальные чебные действия |
||
|
Имеют систематические знания о плоских фигурах и их свойствах |
Познавательные: умеют создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных задач, применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач. Регулятивные: принимают и сохраняют цели и задачи учебной деятельности. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют креативность мышления, инициативность, находчивость, активность п и ешении геомет ических задач |
||
|
О ганизация п ост анства |
|||
|
Фо мы аботы |
Ф онтальная Ф па |
ная (П ; индивид альная (И |
|
|
Образовательные ес сы |
• Учебник. • Задания для па ной аботы |
||
|
этап. Ак ализация оно ных знаний чащихся |
|||
|
ель деятельности |
Совместная деятельность |
||
|
Проверить домашнее задание |
(Ф) Теоретический опрос. 1) Сформулировать и доказать теорему о биссектрисе угла. 2) Сформулировать и доказать теорему, обратную теореме о биссектрисе угла. З С о м ли овать и доказать следствие из тео емы о биссект исе гла |
||
Окончание
|
П этап. Мотивация к деятельности |
||||||
|
Цель деятельности |
Постановка учебной задачи |
|||||
|
Совершенствовать навык решения задач по готовым чертежам с целью подготовки учащихся к восприятию нового материала |
В дано: ВЕ = 4, ВМ= 5. Найти: ИТ.дано: АВ = ВС. Найти: МК.Доказать: вмш АС. 2Рис. З с (Ф) Г•Г2 677.
Доказать. О — центр окружности; АВ, АС и ВС — ее касательные. Доказательство: 1 ) Так как ВО — биссектриса ZCBD, то 0Q Ш) и 0FL ВС равны по свойству биссектрисы угла. 2) Так как СО — биссектриса ZBCk, то 0F Ш ВС и ОМ Ш СК равны по свойству биссектрисы угла. З) В ы в од : 0Q = 0F (из п. 1), 0F= ОМ (из п. 2), следовательно, 0Q = 0F= ОМ— радиусы окружности с центром в точке О, а АВ, ВС, АС — касательные (по определению) Рис. 4 |
|||||
|
III этап. Из чение нового мате иала |
||||||
|
Цель деятельности |
Совместная деятельность |
|||||
|
Ввести понятие серединного перпендикуляра и доказать сопутствующую теорему |
(Ф) . Ввести понятие серединного перпендикуляра, используя рисунок на доске. 2. Доказать теорему о свойстве серединного перпендикуляра. 3. Доказать следствие из этой теоремы. (Доказательство теоремы о серединном перпенДикуляре к- отрезку и следствия из нее желательно В изложить учителю.) Рис. 5 |
|||||
|
IV этап. Зак епление изученного мате нала |
||||||
|
Цель деятельности |
Деятельность чителя |
Деятельность чащихся |
||||
|
Совершенствовать навыт ешения задач |
(Ф) Решить № 679 (6), 680, 682 |
|
||||
|
IV этап. Итоги |
ока. Ре лексия |
|||||
|
Деятельность чителя |
Деятельность учащихся |
|||||
|
— Какое новое понятие узнали на уроке? —С о м ли йте 3 воп оса по сегодняшней теме |
(И) Домашнее задание: 679 (а), 681, 686 (решена в учебнике) |
|||||
У рок 58. Тема: ТЕОРЕМА О ТОЧКЕ ПЕРЕСЕЧЕНИЯ ВЫСОТ ТРЕУГОЛЬНИКА
|
Цель деятельности чителя |
Создать условия для рассмотрения теоремы о точке пересечения высот треугольника и показать ее применение при решении задач |
|
|
Те мины и понятия |
Высота т е гольника, точка пе есечения высот т е голышка |
|
|
Плани емые ез льтаты |
||
|
П едметные мения |
Униве сальные чебные действия |
|
|
Имеют систематические знания о плоских фигурах и их свойствах |
Познавательные: умеют понимать и использовать математические средства наглядности для иллюстрации, интерпретации, аргументации; применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач. Регулятивные: принимают и сохраняют учебные задачи. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют креативность мышления, инициативность, находчивость, активность п и екшеНИИ геомет ических задач |
|
|
О ганизация ост анства |
||
|
Фо мы аботы |
Ф онтальная Ф ; индивид альная И |
|
|
Образовательные ес сы |
• Учебник. • Задания для онтальной, индивид алычой аботы |
|
|
этап. Ак ализация опо ных знаний чащихся |
||
|
ель деятельности |
Совместная деятельность |
|
|
Проверить выполнение домашней работы |
(Ф) Решить устно. 5.
серединные перпендикуляры гэ МС также серединный перпендикуляр 8 э МЕ = 6. |
|
Продолжение
|
П этап. Мотивация из чения новой темы |
|||||
|
ель деятельности |
Постановка чебной задачи |
||||
|
Доказать теорему о точке пересечения высот треугольника |
(Ф) — Какие элементы треугольника пересекаются в одной точке? (Биссектрисы треугольника, серединные перпендикуляры к сторонам треугольника, медианы треугольника.) — В каком треугольнике совпадают точка пересечения биссектрис, точка пересечения медиан, точка пересечения серединных перпендикуляров? (В равностороннем.) — Как вы думаете, пересекаются ли высоты треугольника в одной точке? (Варианты ответов: а) да; б) только в остроугольном; в) в остроугольном и прямоугольном.) В ходе обсуждения выполнить рис. 3 (а, б, в).
Рис. За Рис. 36 Рис. Зв О — точка пересечения высот ЛАВС или их продолжений. 1. Сформулировать и доказать теорему о точке пересечения высот треугольника. Теорема. Высоты треугольника (или их продолжения) пересекаются в одной точке. (Доказать может сам учитель; можно преДложить учащимся разобрать самостоятельно.) 2. Ввести понятие четырех замечательных точек треугольника. Четыре замечательные точки треугольника: 1) Точка пересечения медиан треугольника. 2) Точка пересечения биссектрис треугольника. 3) Точка пересечения серединных перпендикуляров. 4) Точка пе есечения высот т е гольника |
||||
|
III этап. Зак епление из ченного мате иала |
|||||
|
Цель деятельности |
Деятельность учителя |
|
|
|
Деятельность учащихся |
|
|
2 |
|
|
|
3 |
|
Применение теоремы при решении задач |
1. Решить № 683 и 685 у доски и в тетрадях. |
|
М |
Рис. 4 |
дано: МВС, АВ * АС, АМ-медиана. Доказать: АМ не ВС. |
![]() Доказательство:
Доказательство:
l) Примем АМ ВС, следовательно, получим: ММС и ЛАМВ; АЛИ— общая, СМ = МВ (по условию), следовательно, ММС = ММВ (по двум катетам), следовательно, АС АВ, что противоречит условию АВ АС. 2) Значит, наше предположение неверно, а верно АМ не Ш ВС, что и требовалось доказать.
№ 685. с дано: ЛАВС, п ВД = М, АС = ВС, ВД ш АС, АА ВС.
Доказать: СМ Ш Ш, ВК = КА.
Доказательство:
1) Так как АЛ п ВД = М, то СМ Ш АВ (замечательное в А свойство треугольника).
Рис. 5
2) МСК и МСК: СК— общая, ВС = АС (по условию), следовательно, ЛВСК = МСК (по катету и гипотенузе), следовательно, ВК = КА, что и требовалось доказать.
Краткое решение:
Биссектрисы углов треугольника пересекаются в одной точке, следовательно, СМ— биссектриса в ZACB. Пусть СМ п АВ = D. Тогда CD — биссектриса, проведенная к основанию равнобедренного тре-
Рис. 6 угольника CD — высота, то есть CD Ш АВ, значит, СМ -L АВ.
№ 688.
1) Построить биссектрису МЕ угла М.
2) Построить серединный перпендикуляр Е к отрезку АВ — прямую а.
З) а п МЕ = К. К— искомая точка
Окончание
|
IV этап. Итоги ока. Ре лексия |
|
|
еятельность чителя |
Деятельность чащихся |
|
— Назовите четыре замечательные точки треугольника. — Оцените свою работу |
(И) Домашнее задание. в Вариант 1 1.
2. В треугольнике MNk биссектрисы пересекаются в точке О. Расстояние от точки О до стороны MN= 6 см, Nk= 10 см. Найдите площадь треугольника ЛЮК. Вариант II
2. В треугольнике MNk медианы МР и NE пересекаются в точке О и равны 12 и 15 см соответственно. Найдите площадь треугольника МОЕ, если мр -L NE |
Ур о к 59. Тема: ВПИСАННАЯ ОКРУЖНОСТЬ
|
Цель деятельности чителя |
Создать условия для введения понятий вписанной и описанной окружностей, доказательства теоремы об окружности, вписанной вт е гольник |
|
|
Те мины и понятия |
Ок жность, вписанная в т е гольник |
|
|
Плани емые ез льтаты |
||
|
П едметные мения |
Униве сальные чебные действия |
|
|
Владеют базовым понятийным аппаратом по основным разделам содержания |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий; умеют применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач. Регулятивные: принимают и сохраняют цели и задачи учебной деятельности. Коммуникативные: умеют формулировать, аргументировать и отстаивать свое мнение. Личностные: проявляют креативность мышления, инициативность, находчивость, активность п и ешении геомет ических задач |
|
|
|
Организация пространства |
|
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные ресурсы |
• Учебник. • Задания для индивидуальной работы |
|
|
|
этап. Актуализация опорных знаний учащихся |
|
|
Цель деятельности |
Совместная деятельность |
|
|
Проверить выполнение домашнего задания |
(Ф/И). Анализ домашней От в е ты к задачам Вариант 1. 48 0 . 2. 30 см2 |
проверочной работы. проверочной работы: Вариант П 2. 20 см2 |
|
|
|
II этап. Мотивация к деятельности |
|
Цель деятельности |
|
Постановка учебной задачи |
|
Совершенствовать навык решения задач с целью подготовки к восприятию нового материала |
(ФМ). Решение задач на готовых чертежах. Дано: АВ, АС—
касательные, В, С — точки касания. ZBAC =56 , Рис. дано: АВ, ВС, АС- касательные, ИОС = 120 0 , ИВО = 25 0 , ИОС = 1 15 0 . Найти: углы треугольника АОВ. Доказать: О — точка пересечения биссектрис ДАВС
|
|
|
|
III этап. Изучение новой темы |
|
|
Цель деятельности |
Совместная деятельность |
|
|
|
2 |
|
|
Ввести понятие вписанной окружности и доказать теорему о вписанной окружности |
(Ф) Материал предлагается учителем в виде лекции. . Ввести понятие окружности, вписанной в многоугольник. Определение. Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник — описанным около этой окружности. |
|
Продолжение
|
|
2 |
||
|
|
ABCDE — описанный около окружности с центром О пятиугольник.
Аб Рис. З Окружность с центром Q не вписана в четырехугольник ABCD, так как CD не касается окружности. Рис.4 2. Формулировка и доказательство теоремы об окружности, вписанной в треугольник. Теорема. В любой треугольник можно вписать окружность. Для доказательства теоремы можно предложить учащимся самостоятельно решить задачу на построение, а затем обсудить ваианты решений |
||
|
IV этап. Закрепление изученного мате иала |
|||
|
Цель деятельности |
Деятельность чителя |
|
Деятельность чащихся |
|
|
2 |
|
3 |
|
Совершенствовать навыки решения задач |
(Ф/И) Выполнить № 701 (для остроугольного треугольника), 689, 691 |
|
Краткое решение:
Ответ: 20 см. Решение: 1) Центр О вписанной окружности искомого радиуса r лежит на биссектрисе СМ треугольника АВС, а так как СМ Ш АВ, то вписанная окружность касается отрезка АВ в точке М. Поэтому ОМ = r. Обсудить с учащимися различные способы решения этой задачи. |
Окончание
|
|
2 |
|
3 |
|
|
|
|
С пособ 1 .
4) В ДСОм СО = СЛ? + ОМ, то есть (12 - -— 82 + r2 — 24r + r2 = 64 + r2
Способ 2 1) СМ= 2) Отрезок АО — биссектриса треугольника АМС (так как О — центр впи- ОМ АМ санной окружности), поэтому или
|
|
|
V этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
|
Деятельность учащихся |
|
|
— Задайте три вопроса по изученной теме. — Оцените свою работу |
|
(И) Домашнее задание: вопросы 21, 22, с. 1 88; № 701 (для прямоугольного и тупоугольного треугольников), 690, 693 (а, б) |
|
У р о к 60. Тема: СВОЙСТВО ОПИСАННОГО ЧЕТЫРЕХУГОЛЬНИКА
|
Цель деятельности чителя |
Создать условия для выведения свойства описанного четырехугольника и совершенствовать навыки решения задач с использованием свойства описанного четы ех голышка |
|
|
Те мины и понятия |
Ок жность, вписанная в четы ех гольник; описанный четы ех гольник |
|
|
Плани емые ез льтаты |
||
|
П едметные мения |
Униве сальные чебные действия |
|
|
Владеют базовым понятийным аппаратом по основным разделам содержания |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий; умеют применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач. Регулятивные: принимают и сохраняют цели и задачи учебной деятельности. Коммуникативные: формулируют, аргументируют и отстаивают свое мнение. Личностные: проявляют креативность мышления, инициативность, находчивость, активность п и ешении геомет ических задач |
|
|
О ганизация п ост анства |
||
|
Фо мы аботы |
Ф онтальная Ф ; индивид альная И |
|
|
Образовательные ес сы |
• Учебник. • Задания для индивид альной аботы |
|
|
этап. Ак ализация опо ных знаний чащихся |
||
|
ель деятельности |
Задания для индивид альной аботы |
|
|
Проверить выполне- ние домашнего заДаНИЯ |
(И) 1 . Тест с последующей самопроверкой (см. Ресурсный материал). 2. Вызываются несколько учеников, которые на доске показывают решение домашних задач |
|
|
П этап. Мотивация к из чению новой темы |
||
|
Цель деятельности |
Постановка чебной задачи |
|
|
Совершенствовать навыки решения задач на готовых чертежах |
(Ф/И) Решить устно. Найти: радиус окружности, вписанной в треугольник со сторонами 10 см, 10 см, 12 см. Ответ М = З см. Дано: ABCD — равнобедренная трапеция. Найти: DC и АВ.
|
|
Продолжение табл.
|
этап. Изучение нового материала |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Рассмотреть свойство описанного четырехугольника |
(Ф/И) l. Объяснить, что не во всякий четырехугольник можно вписать окружность, на примерах: а) прямоугольника (рис. З); б) параллелограмма (рис. 4). к
Рис. З Рис. 4 2. Сформулировать свойство описанного четырехугольника и предложить учащимся доказать его самостоятельно, а затем заслушать и обсудить варианты доказательств. Теорема. В любом описанном четырехугольнике суммы противоположных сторон равны. 3. Задание для учащихся: сформулировать утверждение, обратное свойству описанного четырехугольника, и выяснить его справедливость (см. задачу № 724) |
|
|
IV этап. Закрепление изученного материала |
||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
Совершенствовать навыки решения задач |
(Ф) 1. На доске и в тетради разобрать решение задачи № 697. (И) 2. Провести самостоятельную работу обучающего харак- тера. Вариант 1 1. В равносторонний треугольник вписана окружность радиусом 4 см. Найдите сторону треугольника. 2. Четырехугольник ABCD описан около окружности. Найдите стороны АВ и CD, если ВС = 6 см, AD = 9 см, АВ в два раза больше, чем CD. Вариант П 1. В равносторонний треугольник со стороной 8 см вписана окружность. Найдите радиус окружности. 2. Четырехугольник ABCD описан около окружности. Найдите стороны ВС и АД если АВ = I см, CD= 1 1 см, ВС в 2 раза меньше AD |
М 697.
Доказать: SAB(7) АВ(У) 2 Рис. 5 Доказательство: S АВЫ)= S АВО+ S вос + S (Т)+ SAOD АЖ D
+ ВС + CD + АД = Самостоятельная работа Вариант Вариант
З 2. 10 см, CD— 5 см. |
Окончание
|
|
V этап. Итоги урока. Рефлексия |
|
|
Деятельность учителя |
|
Деятельность учащихся |
|
— Закончите предложения. • Чтобы в четырехугольник вписать окружность... • Чтобы найти площадь описанного четыреугольника... — Оцените свою або |
|
(И) Домашнее задание: № 696, 697, 698 |
Тест
Вариант 1 1 . Центр вписанной в треугольник окружности совпадает с точкой пересечения его...
а) медиан;
б) биссектрис;
в) серединных перпендикуляров.
2. Центр вписанной в треугольник окружности равноудален от...
а) сторон;
б) углов;
в) вершин треугольника.
З. Центр вписанной в треугольник окружности является точкой пересечения его медиан. Этот треугольник...
а) прямоугольный;
б) равнобедренный;
в) равносторонний. ![]()
4. Окружность называется вписанной в многоугольник, если...
а) все его стороны касаются окружности;
б) все его вершины лежат на окружности;
в) все его стороны имеют общие точки с окружностью.
1 . Радиус вписанной в треугольник окружности равен расстоянию от центра окружности до...
а) сторон треугольника;
б) вершин треугольника;
в) углов треугольника.
2. Центр вписанной в равнобедренный треугольник окружности может лежать...
а) на любой из его высот;
б) одной из его медиан;
в) любом из его серединных перпендикуляров.
З. Центр вписанной в треугольник окружности является точкой пересечения его биссектрис. Этот треугольник может быть...
а) произвольным;
б) только равносторонним;
в) только прямоугольным.
4. Многоугольник называется описанным около окружности, если...
а) окружность имеет общие точки с его сторонами;
б) окружность проходит через его вершины;
в) окружность касается всех его сторон.
|
Ответы к тесту |
|
2 |
з |
4 |
|
Вариант |
6 |
а |
в |
а |
|
Вариант П |
а |
6 |
а |
в |
У рок 61. Тема: ОПИСАННАЯ ОКРУЖНОСТЬ
|
Цель деятельности учителя |
Создать условия для введения понятий описанной около многоугольника окружности и вписанного в окружность многоугольника; рассмотреть теорему об окружности, описанной около треугольника, и показать ее применение при решении задач |
|
|
Термины и понятия |
Описанная окружность около треугольника, вписанный треугольник |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Владеют базовым понятийным аппаратом по основным разделам содержания |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий; умеют применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач. Регулятивные: принимают и сохраняют цели и задачи учебной деятельности. Коммуникативные: умеют формулировать, аргументировать и отстаивать свое мнение. Личностные: проявляют креативность мышления, инициативность, находчивость, активность при решении геометрических задач |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные ресурсы |
• Учебник. • Задания для фронтальной работы |
|
Окончание
|
этап. Актуализация опорных знаний учащихся |
||||
|
Цель деятельности |
Деятельность чителя |
Деятельность учащихся |
||
|
Проверить домашнее задание |
(Ф) Решите устно.
Рис. 2 |
дано: ABCD -ромб, 32, ВС - 20. Найти: r. дано: ABCD— трапеция, СО = 6, OD = 8. Найти: SABCD |
1 . Решение: 1) из ДВОС по теореме Пифагора ОС2 = ВС ос = 12. 1 2) —BD • АС = 32 • = 384. 2
2. Решение: 1) ДСО — прямоугольный, CD = 10. 2)
24; ОК = 4,8; 19,6. |
2 - ОВ2 = 400 -256 = 144
9,6. |
|
|
П этап. Изучение |
новой темы |
|
|
|
Цель деятельности |
|
Совместная деятельность |
|
|
|
Ввести понятие окружности, описанной около многоугольника |
(Ф) 1. Ввести понятия окружности, описанной около 2. Доказать теорему об окружности, описанной около |
многоугольника, и многоугольника, вписанного в окружность. треугольника |
||
|
III этап. Закрепление |
изученного материала |
|||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
||
|
Совершенствовать навыки решения задач |
(ФМ) Решить задачи № 702 (а), 703, 704, 705 (а), 706 |
|
||
|
1V ЭпН. Итоги |
урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
|||
|
— Оцените свою работу на уроке. — Составьте синквейн |
(И) Домашнее задание: № 702 (6), 705 (6), 707, 71 |
|||
У рок 62. Тема: СВОЙСТВО ВПИСАННОГО ЧЕТЫРЕХУГОЛЬНИКА
|
Цель деятельности учителя |
Создать условия для рассмотрения свойства вписанного четырехугольника и показать его применение при решении задач |
|
|
Термины и понятия |
Описанная около четырехугольника окружность, вписанный четырехугольник |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Владеют базовым понятийным аппаратом по основным разделам содержания |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий; умеют применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач. Регулятивные: принимают и сохраняют цели и задачи учебной деятельности. Коммуникативные: формулируют, аргументируют и отстаивают свое мнение. Личностные: проявляют креативность мышления, инициативность, находчивость, активность при решении геометрических задач |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); парная (П); индивидуальная (И); групповая (Г) |
|
|
Образовательные ресурсы |
• Учебник |
|
|
этап. Актуализация опорных знаний учащихся |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Проверить домашнее задание |
(Ф) К доске вызвать двоих учеников и проверить выполнение домашнего задания. N2 707. Решение.
В ЛАВС И = (1 80 0 - 120 0) : 2 = 30 0 . тогда ОВС = 60 0 апос = 60 0 ЛОВС— равносторонний ОВ = ОС = 8 см диаметр равен 16 см. Ответ: 16 см. .N2 711. Решение: Центр описанной около треугольника окружности совпадает с точкой пересечения его серединных перпендикуляров, а радиус окружности равен расстоянию от центра окружности до любой из вершин треугольника. В прямоугольном треугольнике центр описанной около него окружности совпадает с серединой гипотенузы, а радиус равен половине гипотенузы |
|
![]() Продолжение
Продолжение
|
П этап. Решение задач по готовым че тежам |
||||||||
|
Цель деятельности |
Совместная деятельность |
|||||||
|
Повторить изученный материал и подготовить учащихся к восприятию новой темы |
(Ф). 1. 2. з. 7. |
в м А 800 Ответы: ZBAD= |
1. 120 0 , |
Рис. 2 Рис. Рис. 4 Рис. 8 = 35 0 ZBCD = |
Найти: Л. Дано: АВ : Доказать: ABCD — прямоугольник. Найти: АВ, ВС. дано: ЛК = 4. Найти: ОК.
Рис. 9 ; 2. АВ = 5, ВС= 10; З. 4; 4. 60 0 ; 8. ZC= 100 0 , О = 700 ; 9. И + ZC= |
4. А 5. 6. Найти. см; 5. |
|
дано: ЛАВС -равносторонний. ок=з. Найти: АВ. Рис. 5 дано: МВС-равносторонний, Найти: АВ. Рис. б Найти: DC. Рис. 7
Рис. 10
|
|
III этап. Из чение нового мате иала |
||||||||
|
Цель деятельности |
Совместная деятельность |
|||||||
|
|
2 |
|||||||
|
Рассмотреть свойство вписанного четырехугольника |
(Ф). 1. Объяснить, что около четырехугольника не всегда можно описать окружность, на примерах ромба, параллелограмма, не являющихся квадратом и прямоугольником соответственно. 2. Для доказательства теоремы о свойстве вписанного четырехугольника учащимся можно предложить самостоятельно решить задачу с последующим обсуждением. З ад а ч а : Докажите, что в любом вписанном четырехугольнике сумма противоположных углов равна 180 0 . |
|||||||
Окончание
|
|
2 |
|
|
|
З. Для доказательства утверждения, обратного свойству вписанного четырехугольника, предложить з ад а н и е : Сформулируйте утверждение, обратное свойству вписанного четырехугольника, и выясните его истинность (можно по учебнику). Теорема. Если сумма противолежащих углов четырехугольника равна 1 80 0 , то около него можно описать окружность |
|
|
IV этап. Закрепление изученного материала |
||
|
Цель деятельности |
Задания для самостоятельной работы |
|
|
Совершенствовать навыки решения задач |
(Ф) 1. Решить № 708 (а), 710. (И) 2. Выполнить самостоятельную работу. Вариант 1 Центр описанной окружности лежит на высоте равнобедренного треугольника и делит высоту на отрезки 5 см и 13 см. Найдите площадь этого треугольника. Вариант II Меньший из отрезков, на которые центр описанной окружности равнобедренного треугольника делит его высоту, равен 8 см, а основание треугольника равно 12 см. Найдите площадь этого треугольника |
|
|
IV этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
— Оцените свою работу на уроке. — Какой этап урока оказался для вас наиболее сложным? |
(И) Домашнее задание: № 708 (б), 709; № 729 (по желанию) |
|
У р о 63. Тема: РЕШЕНИЕ ЗАДАЧ ПО ТЕМЕ «ОКРУЖНОСТЬ»
|
Цель деятельности учителя |
Создать условия для систематизации теоретического материала главы; совершенствовать навыки решения задач по теме «Окружность» |
|
|
Термины и понятия |
Описанная окружность, вписанная окружность, описанный четырехугольник, вписанный четырехугольник |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Умеют применять изученные понятия, результаты и методы для решения задач |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий. Регулятивные: умеют адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность, контролировать процесс и результат учебной математической деятельности. Коммуникативные: умеют формулировать, аргументировать и отстаивать свое мнение. Личностные: проявляют познавательный интерес к предмету |
|
![]() ПроДол.жение
ПроДол.жение
|
|
Организация пространства |
|
|
Формы работы |
Фронтальная (Ф); индивидуальная (И); парная (П) |
|
|
Образовательные ресурсы |
• Учебник. • Задания для индивидуальной, парной работы |
|
|
|
1 этап. Актуализация опорных знаний учащихся |
|
|
Цель деятельности |
Совместная деятельность |
|
|
Проверить выполнение домашнего задания |
(Ф) 1. Анализ самостоятельной работы. 2. Теоретический тест (см. Ресурсный материал). Тест проводится с целью систематизации теоретического материала. После завершения выполнения работы проводится взаимопроверка. Учитель выводит на экран правильные ответы |
|
|
|
11 этап. Решение задач |
|
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
|
2 |
З |
|
Совершенствовать навыки решения задач |
(Ф) 1. На доске и в тетрадях решить № 719 и 732. |
ZADE — вписанный ZADE = vAE : 2. ZBAD — вписанный ZBAD = vBD : 2. В треугольнике ACD
сумма углов равна 180 0 Л) 732.
С + ZBHM= + ZHMC =180 0 , то есть около данного четырехугольника Рис. 2 можно описать окружность. Вписанные углы МНС и ЛВС опираются на одну и ту же дугу МС, поэтому ДИНС = ZMBC. |
Окончание
|
|
2 |
З |
|
|
(П). 2. Решить в парах задачу. Найдите периметр прямоугольника, вписанного в окружность радиуса 7,5 см, если стороны прямоугольника относятся как 3 : 4 |
Решение:
АС= 2 • см. Рис З ЛАВС-прямоугольный,
АВ : ВС = 3 : 4 по условию задачи (АВ = 3х, ВС = По теореме Пифагора АС2 = АВ2 + ВС2 , то есть (3х) 2 + (4х) 2 = 15 2 , откуда х = 3, АВ = 9 см, ВС = 12 см, тогда = 2 • (9 + 12) см. Ответ: 42 см |
|
III этап. Итоги |
ока. Ре лексия |
|
|
еятельность чителя |
еятельность чащихся |
|
|
— Оцените себя на каждом этапе урока. — Какой этап оказался для вас наиболее сложным? |
(И) Домашнее задание: домашняя самостоятельная работа (см. Ресурсный материал) |
|
Теоретический тест
З а д а н и е : заполните пропуски, чтобы получилось верное утверждение или правильная формулировка определения, теоремы, свойства.
1. Прямая и окружность имеют две общие точки, если расстояние от ... до ... меньше ...
2.
Если прямая АВ — касательная к окружности с центром О и В — точка
касания, то прямая АВ и ... ОВ![]()
3. Угол АОВ является центральным, если точка О является ... а лучи ОА и ОВ ...
4.
Вписанный угол, опирающийся на диаметр![]()
![]()
![]() ZABD = ...
ZAOD =
ZABD = ...
ZAOD =
Если хорды АВ и CD окружности пересекаются в точке Е, то верно равенство ...
7.
 Если АВ -касательная, 14 D секущая, то
выполняется равенство .
Если АВ -касательная, 14 D секущая, то
выполняется равенство .![]()
Рис. З
8.
Если четырехугольник ABCD вписан в окружность, то .![]()
9. Центр окружности, вписанной в треугольник, совпадает с точкой . . .
10.
Если точка А равноудалена от сторон данного угла, то она лежит на![]()
11.
Если точка В лежит на серединном перпендикуляре, проведенному к данному
отрезку, то она![]()
12. Около любого . . . можно описать окружность.
1.
Прямая и окружность имеют только одну общую точку, если расстояние от .
. . до . равно .![]()
2. Если прямая CD проходит через конец радиуса ОК и CD Ш ОК, то CD является к данной окружности.
З. Угол АВС является вписанным, если точка В . . . а лучи ВА
и ВС .![]()
4. Вписанные углы равны, если они . . . на одну . . .
5.
![]() ZABD= . . . ZACD-
ZABD= . . . ZACD-![]()
6. Если отрезки АВ и АС — отрезки касательных к окружности, проведенных из одной точки, то . . .
7.
Если АС и -секущие, то выполняется равенство![]()
![]() 8. Если
четырехугольник описан около окружности, то .
8. Если
четырехугольник описан около окружности, то .![]()
9.
Центр окружности, описанной около треугольника, совпадает с точкой .![]()
10.
Если точка С равноудалена от концов данного отрезка, то она лежит на .![]()
![]() 1. Если точка D лежит на биссектрисе
данного угла, то она
1. Если точка D лежит на биссектрисе
данного угла, то она![]()
12. В любой... можно вписать окружность.
Домашняя самостоятельная работа
1.Две окружности касаются внутренне в точке В, АВ — диаметр большей окружности. Через точку А проведены две хорды, которые касаются меньшей окружности. Угол между хордами равен 60 0 . Найдите длины этих хорд, если:
В ар и ант 1: радиус большей окружности равен R; В ар и ант П: радиус меньшей окружности равен r.
2.Найдите углы треугольника, две стороны которого видны из центра описанной окружности под углами:
Вариант 1: 100 0 и 140 0 . Вариант П: 10 0 и 40 0 .
З. Высота и медиана, проведенные из одной вершины треугольника, делят его угол на части, градусные меры которых относятся как: Вариант 1: 5 : 8 : 5 Вариант П: 4 : 7 : 4.
Найдите углы треугольника.
У р о к 64. Тема: РЕШЕНИЕ ЗАДАЧ ПО ТЕМЕ «ОКРУЖНОСТЬ»
|
|
|
|||||||||||||||||||||||||||
Продолжение
|
этап. Решение задач |
|
|
Цель деятельности |
Совместная деятельность |
|
|
2 |
|
Способствовать подготовке к контрольной работе путем решения задач разного уровня сложности |
1 . Собрать домашние самостоятельные работы. (Г) 2. Каждой группе даются одинаковые задачи. Учащиеся решают их, затем проводится обсуждение и презентация решений. Задача 1. Через точку А окружности проведены диаметр АС и две хорды АВ и AD так, что хорда АВ равна радиусу окружности, точка D делит полуокружность АС на две равные дуги. Найдите углы четырехугольника ABCD, если точки С и D лежат по разные стороны от диаметра АС. Решение: 1) ZABC = ZADC = 90 0 , как вписанные углы, опирающиеся на диаметр. 2) МОВ — равносторонний, так как АО = ВО как радиусы, а хорда АВ равна радиусу, тогда ОАО = 60 0 , осо = 30 0 .
4) ZBAD= ЛАС + ZDAC= 60 0 + - 105 0 . 5) ZBCD = ОСО + ОСА = ЗО О + 45 0 = 75 0 . Задача 2. Основание равнобедренного треугольника равно 1 8 см, а высота, проведенная к нему, равна 12 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей. Решение:
12 см, = R D02 = 12-R, 9 2 + - R)2 . R2 = 81 + 144 -24R + R2 , 24R = 225, R = 9,375. Рис. 2 Центр вписанной окружности также лежит на BD. АО] — биссектриса ZBAC, следовательно АВ : ВЦ — О : Щ. по теореме Пифагора в МВД АВ2 = АО + В» = 81 + 144 =225, значит, АВ = 15 см. Так как ВО2 = R, то: D01 = BD-B02 - = 12 -9,375 во = ва + = 9,375 + 0102 15 • (2,625 - 0102) = 9 (9,375 + 0,02), =-l, 875. Так как 00 < 0 О, лежит между точками В и 02, тогда DOl - ор, = 2,625 + 1,875 -— 4,5 см |
|
П этап. Итоги у ока. Ре лексия |
|
|
Деятельность учителя |
Деятельность ЧаЩИХСЯ |
|
Проанализируйте свою работу в группе, выражая это словами: «помощь», «вместе», «совет», «один», «помогли», «все», «посоветовал», « ассказывал», «под жились», «д уг» и т. п. |
(И) Домашнее задание: решить № 732, 725, 726; подготовиться к контрольной работе |
У рок 65. Тема: КОНТРОЛЬНАЯ РАБОТА ЛЬ 5
|
Цель деятельности чителя |
Создать условия для проверки знаний, умений и навыков учащихся по усвоению и применению изученного материала |
|
||
|
Те мины и понятия |
Ок ужность, дуга ок ужности, адиус, вписанная ок ужность, описанная окружность |
|
||
|
Плани уемые езультаты |
|
|||
|
Предметные умения |
Униве сальные чебные действия |
|
||
|
Умеют демонстрировать знание основных понятий, применять полученные знания для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности |
Познавательные: умеют проводить сравнение, сериацию и классификацию по заданным критериям. Регулятивные: вносят необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок; осуществляют самоанализ и самоконтроль. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: п оявляют познавательный инте ес к изучению п едмета |
|
||
|
О ганизация п ост анства |
|
|||
|
Фо мы аботы |
Фронтальная (Ф); индивидуальная (И); групповая (Г) |
|
||
|
Образовательные есу сы |
• Учебник. • Задания для индивидуальной аботы |
|
||
|
этап. Выполнение конт ольной аботы |
|
|||
|
Цель деятельности |
Задания для кон ольной аботы |
|
||
|
|
2 |
|
||
|
Проверить знания, умения и навыки решения задач |
Вариант 1 . Через точку А окружности проведены диаметр АС и две хорды АВ и АД равные радиусу этой окружности. Найдите углы четырехугольника ABCD и градусные меры дуг АВ, ВС, CD, О. 2. Основание равнобедренного треугольника равно 8 см, а боковая сторона равна 15 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей. Вариант П 1. Отрезок BD — диаметр окружности с центром О. Хорда АС делит пополам радиус ОВ и перпендикулярна ему. Найдите углы четы ехугольника ABCD и градусные ме ы дуг АД ВС, CD, AD. |
|
||
|
|
2 |
|||
|
|
2. Высота, проведенная к основанию равнобедренного треугольника, равна 9 см, а само основание равно 24 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей. Ва р и а нт III (для более подготовленных учащихся) 1. МА и МВ — секущие, АС и BD — хорды окружности с центром О. Докажите, что ZAOB = ZAkB + ZAMB. 2. Площадь равнобедренной трапеции ABCD с основаниями ВС и АД описанной около окружности с центром О и радиусом З см, равна 60 см . Найдите радиус окружности, описанной около треугольника 0CD.
|
|||
|
II этап. Итоги урока. Рефлексия |
||||
|
Деятельность учителя |
Деятельность учащихся |
|||
|
|
(И). Домашнее задание: повторить главу V «Четырехугольники» |
|||
У р о к 66. Тема: ПОВТОРЕНИЕ ПО ТЕМАМ «ЧЕТЫРЕХУГОЛЬНИКИ», «ПЛОЩАДЬ»
|
Цель деятельности учителя |
Создать условия для организации повторения основных теоретических фактов по заданной теме |
|
|||
|
Термины и понятия |
Выпуклые многоугольники, сумма углов выпуклого многоугольника, формулы площадей, параллелограмм, прямоугольник, трапеция, квадрат, ромб |
|
|||
|
Планируемые результаты |
|
||||
|
Предметные умения |
Универсальные учебные действия |
|
|||
|
Умеют применять изученные понятия, результаты и методы для решения задач |
Познавательные: умеют видеть математическую задачу в контексте проблемной ситуации. Регулятивные: умеют адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность. Коммуникативные: умеют формулировать, аргументировать и отстаивать свое мнение, контролировать себя. Личностные: проявляют ответственное отношение к учению, готовность и способность к саморазвитию и самообразованию на основе мотивации к обучению и познанию, выбору дальнейшего образования |
|
|||
|
Организация пространства |
|||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
||||
|
Образовательные ресурсы |
• Учебник. • Задания для индивидуальной работы |
||||
|
этап. Актуализация опорных знаний учащихся |
|||||
|
Цель деятельности |
Совместная деятельность |
||||
|
Систематизировать ошибки, допущенные в контрольной работе |
. Разбор задач, с которыми не справились большинство учеников. 2. Работа над ошибками с использованием ответов и указаний к задачам контрольной работы по необходимости. Индивидуальная помощь учителя менее подготовленным учащимся |
||||
|
П этап. Тест на повторение |
|||||
|
Цель деятельности |
Задания для самостоятельной работы |
||||
|
Проверить уровень сформированности теоретических знаний |
(ФМ) Задания теста выполняются самостоятельно с последующей самопроверкой и обсуждением заданий, в которых допущены ошибки (см. Ресурсный материал) |
||||
|
III этап. Итоги урока. Рефлексия |
|||||
|
Деятельность учителя |
Деятельность учащихся |
||||
|
— Оцените свою работу на уроке. — Какие трудности возникли у вас и почему? |
(И) Домашнее задание: повторить признаки подобия треугольников; решить задачи: 1) На стороне ВС прямоугольника взята точка М так, что АМ= 13 см, АВ 12 см, В = 20 см. Найдите: а) МС; б) площадь четырехугольника АМО. 2) В треугольнике АВС АВ = АС. Высота ВМ равна 9 см и делит боковую сторону на два отрезка так, что АМ= 12 см. Найдите площадь и периметр треугольника |
||||
Ресурсный материал Тест Верно ли, что:
![]() . Сумма углов выпуклого четырехугольника
равна 360 0 .
. Сумма углов выпуклого четырехугольника
равна 360 0 .
З. Квадрат — это параллелограмм, у которого все углы прямые.
4. Вершины А и С ромба ABCD симметричны относительно прямой BD.
5. Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные им отрезки.
6. Отрезок, соединяющий точки, лежащие на боковых сторонах трапеции, параллелен основаниям и равен их полусумме.
7. Параллелограмм, у которого все углы равны и все стороны равны, является квадратом.
8. Биссектриса одного из углов параллелограмма отсекает от него равнобедренный треугольник.
9. Площадь прямоугольной трапеции равна произведению ее средней линии на боковое ребро. Ш. Площадь ромба равна половине произведения его диагоналей на синус угла между ними.
1 1. Если в треугольниках АВС и AlBlCl высоты АН и AlHl равны, то SABC : sА вс = вс : вс. 12. Площадь прямоугольного треугольника равна произведению его катетов.
13.
Если в ЛАВС стороны равны 5, 6, 7 см, то его площадь равна 18(18 — 5)(18
— 7) см2![]()
14. Если в треугольниках АВС и AIBlC1 И = ZAl, то SABC : sА вс = (АВ • АС) : (АД • AlCl).
1 5. Медианы треугольника делят треугольник на шесть равновеликих треугольников.
Укажите верный ответ из предложенных:
1. Сумма углов выпуклого пятиугольника равна:
а) 360 0 ; 6) 9000 ; в) 540 0 .
2. Один из углов равнобедренной трапеции равен 100 0 . Три оставшихся угла равны:
а) 80 0 , 80 0 , 100 0 ; 6) 75 0 , 75 0 , 100 ; в) 70 0 , 70 0 , 120 0 .
3. Смежные стороны прямоугольника равны 6 и 8 см. Диагонали его равны:
![]() б) 10 и 10 см; в)
14 и 14 см.
б) 10 и 10 см; в)
14 и 14 см.
4. Сторона ромба равна 5 см, а одна из его диагоналей 6 см. Площадь ромба равна:
а) 30 см- б) 24 см2. в) 15 см-.
5. В ромбе ABCD И = 70 0 , ЛВС равен:
а) 20 0 ; в) 55 0 .
6. В параллелограмме разность смежных сторон равна 5 см, а его периметр равен 38 см. Меньшая сторона параллелограмма равна:
а) 7 см; б) 12 см; в) 9,5 см. 7. Биссектриса угла А прямоугольника ABCD пересекает ВС в точке Е так. что ВЕ = 4,5 см, СЕ = 5,5 см. Площадь прямоугольника равна:
а) 55 см2. 6) 100 см 2 в)
45 см2 ![]() 8. Одна из диагоналей ромба равна его
стороне. Углы ромба равны:
8. Одна из диагоналей ромба равна его
стороне. Углы ромба равны:
а) 90 0 , 90 0 , 90 0 , 90 0 , 6) 60 0 , 60 0 , 1200 , 120 0 ; в) 45 0 , 45 0 , 90 0 , 90 0 .
9. Ромб, не являющийся квадратом, имеет п осей симметрии. Значение п равно:
10.Площадь ромба со стороной 8 см и углом 60 0 равна:
а) 32 см2. 6) 326
см 2 в)
1645 см 2![]()
1 . Площадь прямоугольника с гипотенузой 26 см, один из катетов которого равен 24 см, равна:
а) 120 см- б)
312 см- в) 240 см2![]()
12. Площадь равнобедренного треугольника с боковой стороной 13 см и основанием 24 см равна:
2
а) 120 см б)
156 см- в) 60 см ![]()
13. Одна из сторон параллелограмма равна 14 см, а высота, проведенная к ней, — 12 см. Высота, проведенная к смежной стороне, равной 21 см, равна:
а) 8 см; б) 10 см; в) 19 см. 14. Площадь равнобедренной трапеции с основаниями 10 см и 16 см и боковой стороной 5 см равна:
а)
104 см2. б) 52 см- в) 65
см-![]()
15. Площадь квадрата со стороной 5 ф см равна:
а)
50 см2. 6) 25 см 2 в)
100 см-![]()
Ответы к первой части теста:
Верно: 1, 4, 5, 7, 8, 10, П, 14, 15. Неверно: 2, З, 6, 9, П, В.
|
|
2 |
з |
4 |
5 |
|
7 |
|
9 |
|
1 1 |
12 |
|
14 |
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
От в е ты ко второй части теста:
У р о к 67. Тема: ПОВТОРЕНИЕ ПО ТЕМАМ «ПОДОБНЫЕ ТРЕУГОЛЬНИКИ», «ОКРУЖНОСТЬ»
|
Цель деятельности учителя |
Создать условия для организации повторения основных теоретических фактов по заданной теме |
|
|
Термины и понятия |
Подобные треугольники, сходственные стороны, пропорциональные отрезки |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
|
2 |
|
|
Умеют применять изученные понятия и методы для реШеНИЯ задач |
Познавательные: умеют видеть математическую задачу в контексте проблемной ситуации. Регулятивные: умеют адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность. Коммуникативные: умеют формулировать, аргументировать и отстаивать свое мнение, контролировать себя. Личностные: проявляют ответственное отношение к учению, готовность и способность к саморазвитию и самообразованию на основе мотивации к обучению и познанию, выбору дальнейшего об азования |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные ес сы |
• Учебник. • Задания для па ной, индивид альной аботы |
|
|
этап. Ак ализация опо ных знаний чащихся |
||||
|
ель деятельности |
Совместная деятельность |
|||
|
Проверить правильность выполнения домашнего задания |
(Ф/И) Двое желающих учащихся у доски показывают решение домашнего задания. Остальные решают устно задачи.
2.На рис. 2 точка О — центр окружности, АС и ВС — касательные к окружности, ИОВ = 140о Найдите: С. см
Рис. З Ответ: 1 70
, |
|||
|
II этап. Решение задач |
||||
|
Цель деятельности |
Деятельность учителя |
|
Деятельность учащихся |
|
|
|
|
2 |
|
З |
|
Совершенствовать навыки решения задач |
(П) 1 . Найти.• ЛВС.
|
|
: З. Найти: РМ. 20 м к Рис. 8 |
Ответ ы : 1) ЛВС = 70 0 . 2) ИСЕ = 30 0 . 3) ZMEP = 700 . 4) 18.
6) ZBAD= 105 0, ZBCD = 75 0 . |
|
|
|
2 |
3 |
|
|
2. Найти: ИСЕ. с
З. Найти: ZMEP.
Рис. 6 4. СР в 2 раза меньше PD. Найти: СД
9. ABCD — трапеция, АВ + CD Найти: О, АВ, СД |
6.
Найти • ZBAD, ZBCD. Рис. 9 7. Найти.• СН, ВС, АС. в
Рис.1О 8. МК = 8. Найти: РК.
— 15.
|
7) СН- 36,
|
|
IlI этап. Тест |
|||
|
Цель деятельности |
Задания для самостоятельной работы |
||
|
Проверить уровень теоретических знакЛИп llV |
(И) Тест (см. Ресурсный материал) |
||
![]()
|
|
IV этап. Итоги урока. Рефлексия |
|||||
|
Деятельность учителя |
|
Деятельность учащихся |
||||
|
|
|
2 |
||||
|
(ФМ). — Оцените свою работу на уроке, работу в паре |
|
(И) 1. сота а) 7 2. а) 30 6) 45 в) 60 з. 4. 5. 6. |
Домашнее Высота, никаАВС к равна: см; б) 10 Диагонали 0 , 150 0 , 0 , 135 0 , 0 , 1200 ,
с 700 600 |
проведенная гипотенузе см; ромба 30 0 , 45 0 ,
60 0 ,
|
задание: из АС, в) см. равны 1 50 0 , 135 0 ; 120 0 . зоо зоо |
вторую часть теста учащиеся выполняют дома. прямого угла вершины прямоугольного треугольделит ее на отрезки, равные 25 см и 4 см. Эта вы- 4 см и 4$ см. Его углы равны: Величина дуги ВтС равна: а) 120 0 ; 6) 240 0 ; в) 600 . По данным рисунка, величина угла ТС равна: а) 140 0 ; 6) 35 0 ; в) 70 0 . По данным рисунка, величина угла BED равна: а) 50 0 ; 6) 200 ; в) 40 0 . По данным рисунка, величина угла САЕ равна: а) 20 0 ; 6) 40 0 ; в) 30 0 . |
![]()
|
|
|
2 |
|
|
7.
D
8.с к 9. Квадрат вписан в а) 32 см; 6)16Ji см; |
По данным рисунка, углы четырехугольника равны: а) 90 0 , 90 0 , 1000 , 120 0 ; 6) 90 0 , 90 0 , 80 0 , 100 0 ; в) 900 , 90 0 , 100 0 , По данным рисунка, длина стороны AD равна:
окружность диаметра 8 см. Периметр квадрата равен: в) 16 см |
Ресурсный материал Тест Установите, верно ли Данное утверлсДение:
1 . Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.
2. Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.
З. На рисунке ЛВС = ZBCD.
4. Если хорды МЛ/ и КР параллельны, то градусные меры дуг МК и NP равны.
5.
Градусная мера дуги АТС, изображенной на рисунке, равна 75 0![]()
6. Углы треугольника АВС,
изображенного на рисунке, равны 30 0 , 30 0 , 120 ![]() в
в
7. Точки А и В делят окружность на две дуги, ббльшая из которых равна 200 0 , а меньшая точкой К делится в отношении 5 : З, считая от точки А. Тогда дуга АК = 1000 .
8. Длина хорды АВ, изображенной на рисунке, равна 12 см.
9.
На рисунке АВ = 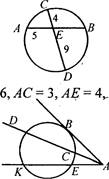 % тогда AD =
% тогда AD =![]()
Ответы к тесту.
Верно: 1, 2, 4, 7. Неверно: 3, 5, 6, 8, 9.
У рок 68. Тема: ИТОГОВОЕ ПОВТОРЕНИЕ
|
Цель деятельности учителя |
Создать условия для повторения основных теоретических фактов по заданной теме |
|
|
Те мины и понятия |
Окружность, вписанная в т еугольник; т апеция, площадь т апеции |
|
|
Планируемые результаты |
||
|
П едметные мения |
Универсальные учебные действия |
|
|
|
2 |
|
|
Умеют применять изученные понятия, результаты и методы для решения задач |
Познавательные: умеют видеть математическую задачу в контексте проблемной ситуации. Регулятивные: умеют адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность. Коммуникативные: умеют формулировать, аргументировать и отстаивать свое мнение, конт олировать себя, работать в группе. |
|
ПроДол.жение
|
|
|
2 |
|||
|
|
|
Личностные: проявляют ответственное отношение к учению, готовность и способность к саморазвитию и самообразованию на основе мотивации к обучению и познанию, выбору дальнейшего образования |
|||
|
|
О ганизация п ост анства |
||||
|
Фо мы аботы |
Ф онтальная Ф • индивид альная И ; г пповая Г |
||||
|
Образовательные ес сы |
• Учебник. • Задания для г пповой аботы |
||||
|
|
этап. Ак ализация опо ных знаний чащихся |
||||
|
ель деятельности |
Совместная деятельность |
||||
|
Проверить домашнее задание |
Ф Учитель выводит на эк ан или на доску правильные ответы домашнего теста:
|
||||
|
|
П этап. Решение задач |
||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|||
|
|
2 |
|
|||
|
Совершенствовать навыки решения задач |
(Г). Класс разбить на несколько групп. Учащиеся 20 минут работают в группах, а затем демонстрируют свои решения, после обсуждения выставля- ются оценки. Задач и : 1 . Найдите радиус окружности, вписанной в треугольник, и радиус окружности, описанной около треугольника, стороны которого равны 20 см, 26 см и 26 см. 2. Расстояния от центра вписанной в прямоугольную трапецию окружности до концов большей боковой стороны равны 6 см и 8 см. Найдите площадь трапеции. 3. Точка О равноудалена от сторон треугольника АВС, ИСО = 34 0 . Найдите ZAOB |
Краткое решение:
Рис. 2 26 АВ : Щ : Щ;
(24 - = 100 9—см, 12 12
: (CD : 2) = 4,8 см, значит, АВ = 9,6 см. D Рис. З Ж) = SAB(D |
|||
Окончание
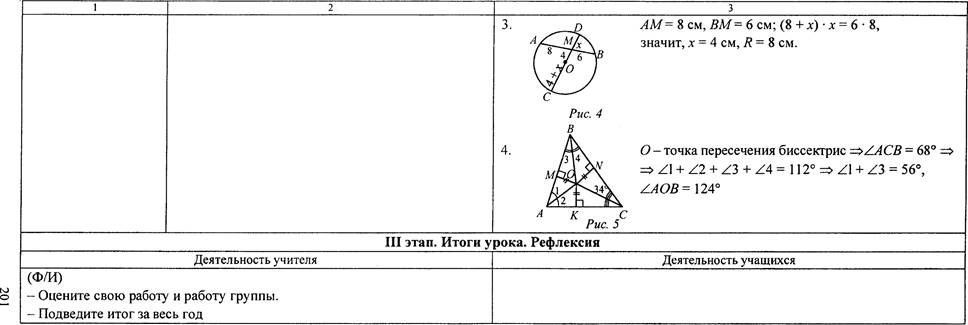
У р о к 69. Тема: ИТОГОВОЕ ПОВТОРЕНИЕ
|
Цель деятельности учителя |
Создать условия для организации повторения основных теоретических фактов по заданной теме |
|
|
Термины и понятия |
Окружность, вписанная в треугольник, квадрат, прямоугольная трапеция |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Умеют применять изученные понятия, результаты и методы для решения задач |
Познавательные: умеют видеть математическую задачу в контексте проблемной ситуации. Регулятивные: умеют адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность. Коммуникативные: умение формулировать, аргументировать и отстаивать свое мнение, контролировать себя, работать в группе. Личностные: проявляют ответственное отношение к учению, готовность и способность к саморазвитию и самообразованию на основе мотивации к обучению и познанию, выбору дальнейшего образования |
|
Окончание
|
О ганизация п ост анства |
||
|
Фо мы аботы |
Ф онтальная Ф па ная П ; г пповая Г |
|
|
Образовательные ес сы |
• Учебник. • Задания для па нои и г пповой аботы |
|
|
этап. Акт ализация опо ных знаний чащихся |
||
|
ель деятельности |
Совместная деятельность |
|
|
Совершенствовать теоретические знания |
(П) Решить кроссворд (см. Ресурсный материал) |
|
|
П этап. Решение задач |
||
|
ель деятельности |
Совместная деятельность |
|
|
Совершенствовать навыки решения задач, повторяя теоретический материал |
(Г) Класс разбивается на 5 групп: каждая группа решает одну задачу. 1 . Два соседних угла вписанного четырехугольника равны 120 0 и 150 0 . Найдите градусные меры дуг, на которые опираются два других угла четырехугольника. 2. Сторона равностороннего треугольника равна 6 см. Найдите радиус вписанной окружности. З. Определите площадь квадрата, описанного около окружности с радиусом r. 4. Радиус окружности, вписанной в прямоугольную трапецию, равен 12 см, а наибольшая боковая сторона трапеции — 25 см. Найдите периметр трапеции. a+b—c 5. В прямоугольный треугольник с катетами а и Ь и гипотенузой с вписана окружность радиуса r. Докажите, что r = 2 После того, как все г ппы готовы, они п едставляют ешения задач |
|
|
III этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
— Какие свойства, теоремы, признаки пришлось вспомнить, чтобы решить задачи? — Оцените свою або и абот г ппы |
(И) Домашнее задание: решить задачу. В окружности проведены две хорды ЛИЛ и РК, пересекающиеся в точке Е. 14 см, МЕ на 2 см больше ЛЕ. Найти площадь треугольника PNE, если площадь т е голышка МЕК авна 64 см2 |
|
Ресурсный материал Кроссворд Вопросы:
1. Многоугольник, у которого четыре стороны. (Четырехугольник.)
2. Многоугольник, у которого противоположные стороны попарно параллельны. (Параллелограмм.)
З. Что в параллелограмме при пересечении делится пополам? (Диагональ.)
4. Как называется утверждение «если в четырехугольнике противоположные стороны попарно равны, то он — параллелограмм»? (Признак.)
5. Четырехугольник с двумя непараллельными сторонами. (Трапеция.)
6. Трапеция, у которой углы при основании равны. (Равнобедренная.)
• 7. Какой многоугольник лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины. (Выпутый.)
8. Один из этапов решения задачи на построение. (Доказательство.)
9. Четырехугольник, у которого диагонали равны. (Прямоугольник.)
![]() 1 . Прямоугольник с равными сторонами.
(КваДрат.)
1 . Прямоугольник с равными сторонами.
(КваДрат.)
12. Чем являются диагонали ромба по отношению к его углам. (Биссектриса.)
13. Одна из сторон равнобедренной трапеции. (Основание.)
14.
Если трапеция прямоугольная, то у нее один из углов... (прямой).
Урок 70. Тема: ИТОГОВОЕ ПОВТОРЕНИЕ
|
Цель деятельности учителя |
Создать условия для организации повторения основных теоретических фактов по заданной теме |
|
|
Термины и понятия |
Окружность, вписанная в треугольник, квадрат, прямоугольная трапеция |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Умеют применять изученные понятия, результаты и методы для решения задач |
Познавательные: умеют видеть математическую задачу в контексте проблемной ситуации. Регулятивные: умеют адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность. Коммуникативные: умеют формулировать, аргументировать и отстаивать свое мнение, контролировать себя, работать в группе. Личностные: проявляют ответственное отношение к учению, готовность и способность к саморазвитию и самообразованию на основе мотивации к обучению и познанию, выбору дальнейшего образования |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И); групповая (Г) |
|
|
Образовательные ресурсы |
• Учебник. • Задания для индивидуальной и групповой работы |
|
|
этап. Актуализация опорных знаний учащихся |
||
|
Цель деятельности |
Задания для самостоятельной работы |
|
|
Повторить теоретический материал |
(И) Математический диктант (с взаимопроверкой): 1 . Дополните предложение: «Многоугольник называется правильным, если его... » 2. Найдите количество углов правильного многоугольника, если сумма его углов равна 1 800 0 . З. Закончите предложение: «Если один из углов параллелограмма равен 27 0 , то другие углы равны... » 4. Одна из сторон прямоугольника на 8 см больше соседней стороны. Найдите периметр прямоугольника. 5. Сторона прямоугольника в З раза больше соседней стороны, его периметр равен 1 6 см. Найдите периметр квадрата, построенного на меньшей стороне прямоугольника. 6. Площадь треугольника равна 1 7 см-. Найдите площадь параллелограмма, построенного на смежных сторонах. 7. Определите вид треугольника, если его стороны равны 20 см, 16 см, 12 см. 8. Найдите площадь треугольника со сторонами 16 см, [2 см, 20 см. 9. Пропорциональны ли отрезки АВ, CD, АД, ClDl, если их отношения равны 45 : 12 = 9 : 4? l0. Найдите коэффициент подобия треугольников, если их площади относятся как • 16. I 1. Закончите предложение: «Угол называется вписанным в окружность, если... » 12. Если центральный угол равен 126 0 , найдите вписанный угол, который опирается на ту же самую дугу, что и центральный. 13. Закончите
предложение: «Вписанный угол, опирающийся на полуокружность...» |
|
Окончание табл.
|
П этап. Решение задач |
||
|
ель деятельности |
Совместная деятельность |
|
|
Совершенствовать навыки решения задач |
(Г) Работу по группам можно организовать в форме соревнования. Задания каждая группа получает одинаковые. Выигрывает та группа, которая решила задачу быстро и верно. 1. Два соседних угла вписанного четырехугольника опираются на дуги, градусные меры которых равны 192 0 и 214 0 . Найдите два других угла четырехугольника. 2. Сторона равностороннего треугольника равна 6 см. Найдите радиус описанной вокруг треугольника окружности. 3. Определите площадь ромба со стороной а, описанного около окружности с диаметром d. 4. Периметр прямоугольной трапеции, описанной около окружности, равен 98 см, а радиус окружности — 12 см. Найдите наибольшую боковую сторону. 5. Прямоугольный треугольник с катетами а и Ь описан около окружности радиуса r и вписан в окружность радиуса R. Докажите, что 2R + 2r = а + Ь |
|
|
III этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
— Оцените свою работу и работу группы. — Закончите предложения. • В этом году я узнал.. • Я научился... • Я умею... |
|
|
ЛИТЕРАТУРА
1. Атанасян, Л. С. Изучение геометрии в 7—9 классах : пособие для учителей общеобразоват. учреждений / Л. С. Атанасян, В. Ф. Бутузов, Ю. А. Глазков, В. Б. Некрасов, И. И. Юдина. — 7-е изд. — М. : Просвещение, 2009.
2. Балин, Э. Н. Геометрия : задачи на готовых чертежах для подготовки к ГИА и ЕГЭ. 7—9 классы / Э. Н. Балаян. — 5-е изд., испр. и доп. — Ростов нД : Феникс, 2013.
З. Геометрия. 8 класс : поурочные планы по учебнику Л. С. Атанасяна [и др.] / авт.-сост. Т. Л. Афанасьева, Л. А. Тапилина. — 4-е изд., испр. — Волгоград : Учитель, 2013.
4. Геометрия. Сборник рабочих программ. 7—9 классы : пособие для учителей общеобразоват. учреждений / сост. Т. А. Бурмистрова. — М. : Просвещение, 20] .
5. Ершова, А. П. Самостоятельные и контрольные работы по алгебре и геометрии для 8 класса / А. П. Ершова, В. В. Голобородько, А. С. Ершова. — М. : Илекса ; Харьков : Гимназия, 2001.
6. Зив, Б. Г. Задачи по геометрии : пособие для учащихся 7—1 классов / Б. Г. Зив, В. М. Мейлер, А. Г. Баханский. — М. : Просвещение, 2003.
7. Примерные программы по учебным предметам. Математика. 5—9 классы : проект. — 3-е изд., перераб. — М. : Просвещение, 201 1.
8. Рабинович, Е. М Геометрия : задачи и упражнения на готовых чертежах. 7—9 классы / Е. М. Рабинович. — Харьков : Гимназия, 1998.
9.
Фарсов, А. В.
Тесты по геометрии. 8 класс : к учебнику Л. С. Атанасяна и др. «Геометрия. 7—9
классы» / А. В. Фарков. — М. : Экзамен, 2009.
СОДЕРЖАНИЕ
![]() ВВЕДЕНИЕ
ВВЕДЕНИЕ
Урок З. Тема.• Параллелограмм. Свойства параллелограмма
У ро к 4. Тема: Признаки параллелограмма![]() 12
12
Урок 5. Тема.• Решение задач по теме «Параллелограмм»![]() 16
16
Урок 6. Тема: Трапеция![]()
Урок 7. Тема.• Решение задач по теме «Параллелограмм.
Трапеция»![]() 22
22
Урок 8. Тема: Трапеция. Задачи на построение![]() 26
26
У ро к 9. Тема: Прямоугольник![]() 29 Урок 10. Тема: Ромб. Квадрат
29 Урок 10. Тема: Ромб. Квадрат![]() 32
32
Урок 11. Тема: Решение задач![]() 36
36
Урок 12. Тема: Осевая и центральная симметрия![]() 38
38
Урок 13. Тема: Решение задач![]() 40
40
Урок 14. Тема: Контрольная работа № 1![]() 44
44
Глава И. Площадь![]() 45
45
Урок 15. Тема: Площадь многоугольника![]() 45 Урок 16. Тема: Площадь
многоугольника
45 Урок 16. Тема: Площадь
многоугольника![]() 48 Урок 17. Тема: Площадь параллелограмма
48 Урок 17. Тема: Площадь параллелограмма![]() 51 Урок 18. Тема: Площадь треугольника
51 Урок 18. Тема: Площадь треугольника![]() 55 Урок 19. Тема: Площадь
треугольника
55 Урок 19. Тема: Площадь
треугольника![]() 59
59
Урок 20. Тема: Площадь трапеции![]() 62
62
Урок 21.
Тема: Решение задач на вычисление площадей фигур![]() 66 Урок 22. Тема: Решение задач на
вычисление площадей фигур
66 Урок 22. Тема: Решение задач на
вычисление площадей фигур![]() 69
69
Урок 23. тема: Теорема Пифагора![]() 71
71
Урок 24. тема: Теорема, обратная теореме Пифагора![]() 74 Урок 25. Тема: Решение задач на
применение теоремы Пифагора
74 Урок 25. Тема: Решение задач на
применение теоремы Пифагора![]() 79
79
Урок 26.
Тема: Решение задач на применение теоремы Пифагора. Формула Герона![]() 83 Урок 27. Тема: Решение задач на
применение теоремы Пифагора. Формула Герона
83 Урок 27. Тема: Решение задач на
применение теоремы Пифагора. Формула Герона![]() 86
86
Урок 28. тема.• Контрольная работа № 2![]() 88
88
Глава VII. Подобные треугольники![]() 91
91
Урок 29. Тема: Пропорциональные отрезки. Определение
подобных треугольников![]()
Уро к 30. Тема: Отношение площадей подобных
треугольников![]() 93 Урок 31. тема: Первый признак подобия треугольников
93 Урок 31. тема: Первый признак подобия треугольников![]() 97
97
Урок 32. Тема: Первый признак подобия треугольников.
Решение задач![]() lOl
lOl
Урок 33. Тема: Второй и третий признаки подобия
треугольников![]() 104 Урок 34. Тема: Решение задач на применение признаков подобия
треугольников
104 Урок 34. Тема: Решение задач на применение признаков подобия
треугольников![]() 106
106
Урок 35. Тема: Решение задач на применение признаков
подобия треугольников![]() 109
109
Урок 36. Тема: Контрольная работа № З![]()
Урок 37. тема: Средняя линия треугольника![]() 115 Урок 38. тема.• Средняя линия
треугольника
115 Урок 38. тема.• Средняя линия
треугольника![]() 118
118
Урок 39. Тема: Пропорциональные отрезки в
прямоугольном треугольнике![]() 121 Урок 40. Тема.• Пропорциональные отрезки в прямоугольном треугольнике
121 Урок 40. Тема.• Пропорциональные отрезки в прямоугольном треугольнике![]() 123
123
Урок 41.Тема: Измерительные работы на местности![]() 126 Урок 42.Тема: Задачи на
построение методом подобия
126 Урок 42.Тема: Задачи на
построение методом подобия![]() 129 Урок 43. Тема.• Задачи на построение методом подобия
129 Урок 43. Тема.• Задачи на построение методом подобия![]() 132
132 ![]() о к 44. Тема.• Синус, косинус и
тангенс острого угла прямоугольного треугольника
о к 44. Тема.• Синус, косинус и
тангенс острого угла прямоугольного треугольника![]() 134 У ро к 45. Тема: Значения синуса,
косинуса и тангенса для углов 300 , 45 0 и 600
134 У ро к 45. Тема: Значения синуса,
косинуса и тангенса для углов 300 , 45 0 и 600![]() 135 Урок 46. Тема.' Соотношения между
сторонами и углами прямоугольного треугольника.
135 Урок 46. Тема.' Соотношения между
сторонами и углами прямоугольного треугольника.
Решение задач![]() 139 У ро к 47. Тема: Подготовка к
контрольной работе
139 У ро к 47. Тема: Подготовка к
контрольной работе![]() 141 У ро к 48. Тема: Контрольная работа № 4
141 У ро к 48. Тема: Контрольная работа № 4![]() 145 Глава VIII. Окружность
145 Глава VIII. Окружность![]() 146
146
Урок 49. Тема: Взаимное расположение прямой и
окружности![]()
Урок 50. тема: Касательная к окружности![]() 149
149
Урок 51.
тема: Касательная к окружности. Решение задач![]() 151 Урок 52. Тема: Градусная мера
дуги окружности
151 Урок 52. Тема: Градусная мера
дуги окружности![]() 154 Урок 53. Тема: Теорема о вписанном угле
154 Урок 53. Тема: Теорема о вписанном угле![]() 156
156
Урок 54. Тема: Теорема об отрезках пересекающихся хорд![]() 160
160
Урок 55. тема: Решение задач по теме «Центральные и
вписанные углы»![]() 162
162
Урок 56. тема: Свойство биссектрисы угла![]() 165 Урок 57. Тема: Серединный
перпендикуляр
165 Урок 57. Тема: Серединный
перпендикуляр![]() 168
168
Урок 58. тема.• Теорема о точке пересечения высот
треугольника![]()
Урок 59. Тема: Вписанная окружность![]() 173
173
Урок 60. Тема.• Свойство описанного четырехугольника![]() 177
177
Урок Ы. Тема: Описанная окружность![]() 180
180
Урок 62. Тема: Свойство вписанного четырехугольника![]() 182 Урок 63. тема: Решение задач по
теме «Окружность»
182 Урок 63. тема: Решение задач по
теме «Окружность»![]() 184
184
Урок 64. Тема: Решение задач по теме «Окружность»![]() 188
188
Урок 65. Тема: Контрольная работа № 5![]() 190
190
Урок 66. Тема: Повторение по темам «Четырехугольники»,
«Площадь»![]() 191
191
Урок 67. тема: Повторение по темам «Подобные
треугольники», «Окружность»![]()
Урок 68.
тема: Итоговое повторение![]() 199 Урок 69. Тема: Итоговое повторение
199 Урок 69. Тема: Итоговое повторение![]() 201 Урок 70. Тема: Итоговое
повторение
201 Урок 70. Тема: Итоговое
повторение![]() 204 Литература
204 Литература![]() 206
206
Охраняется законом об авторском праве. Воспроизвеоение всего пособия или любой его части, а также реализация тиража запрещаются без письменного разрешения издателя. Любые попытки нарушения закона будут преследоваться в судебном поряДке.
Приглашаем к сотрудничеству учителей, методистов и других специалистов в области образования для поиска и рекомендации к публикации интересных материалов, разработок, проектов по учебной и воспитательной работе. Издательство «Учитель» выплачивает вознаграждение за работу по поиску материала. Издательство также приглашает к сотрудничеству авторов и гарантирует им выплату гонораров за предоставленные работы.
Телефон: (8442) 42-17-71; 42-23-41; 42-23-52. E-mail: met@uchitel-izd.ru
Подробности см. на сайте издательства «Учитель»: www.uchitel-izd.ru
Информацию о продукции издательства, вебинарах и других формах работы с педагогами, новости образования см. в интернет-магазипе «УчМаг»: www.uchmag.ru и на портале для педагогов «Учмет»: www.uchmet.ru
ГЕОМЕТРИЯ
Технологические карты уроков по учебнику
Л. С. Атанасяна, В. Ф. Бутузова, С. Б. Кадомцева, Э, Г. Позняка, И. И. Юдиной
Автор-составитель
![]()
![]() Галина
Юрьевна Ковтун
Галина
Юрьевна Ковтун
Ответственные за выпуск
Л. Е. Гринин, Н. Е. Волкова-Алексеева Редакторы-методисты Г. П. Попова, Е. А. Виноградова
Технический редактор Н. М. Болдырева Редактор-корректор М. И. Ромаданова
Компьютерная верстка С. А. Волобуевой Дизайн обложки Н. А. Цибаиовой
Издательство «Учитель»
400079, г. Волгоград, ул. Кирова, 143
![]()
Подписано в
печать 21.05.14. Формат 60 х 84/8. ![]()
Бумага газетная. Гарнитура Тип Таймс. Печать офсетная.
Усл. печ. л. 24,65. Тираж 7 500 экз. (1-й з-д 1—2 500). Заказ № 542.
Отпечатано с оригинал-макета в ОАО «Калачевская типография». 404507, Волгоградская обл., г. Калач-на-Дону, ул. Кравченко, 7.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.