Текстовые задачи в профильном уровне ЕГЭ по математике.

Текстовые задачи  в профильном уровне ЕГЭ по математике.

                                                               

                             

Текстовые задачи  являются важной составляющей  школьного курса математики, поэтому наличие таких задач  в  ЕГЭ оправдано и необходимо для оценки общей математической подготовки выпускников. Предложенные для решения на экзамене задачи стандартные. И особых вопросов эти задания вызывать не должны.

Однако изучение текстовых задач происходит в основной школе, рассматриваются они недостаточно основательно, поэтому приобретённые в основной школе навыки и знания решения таких задач со временем теряются. Для того чтобы успешно справляться с этими заданиями, необходимо в ходе подготовки к ЕГЭ  повторить классификации задач, а также систематизировать знания  по математике.

Все текстовые задачи  можно  условно классифицировать по типам: задачи на числовые зависимости; задачи, связанные с понятием процента; задачи на «движение», «концентрацию смесей и сплавов», «работу» и т. д.

По методу решения задачи делятся на задачи решаемые: арифметическим методом, алгебраическим методом и геометрическим методом.

Арифметический метод. Решить задачу арифметическим методом значит найти ответ на требование задачи посредством выполнения арифметических действий над числами. Одну и ту же задачу можно решить различными арифметическими способами.

Алгебраический метод. Решить задачу алгебраическим методом – это значит найти ответ на требование задачи, составив и решив уравнение или систему уравнений (или неравенств).

При решении задач алгебраическим методом основная деятельность учащегося сосредотачивается на первом этапе решения задачи: на разборе условия задачи  при составлении уравнений или неравенств по условию задачи.

Вторым этапом является решение составленного уравнения или системы уравнений, неравенства или системы неравенств.

Третьим важным этапом решения задач является проверка решения задачи, которая проводится по условию задачи.

Геометрический метод. Он состоит в том, что решение задачи сопровождается наглядным представлением, иногда доказательство или решение видно из наглядной картины. Под геометрическим методом решения алгебраических задач  понимается метод решения, заключающийся в использовании геометрических представлений (изображений), законов геометрии и элементов аналитических методов (уравнений или неравенств), систем уравнений, арифметических выражений и др.

Рассмотрим один из распространенных типов задач – задачи на работу.

Эти задачи содержат в себе информацию о выполнении некоторой работы несколькими субъектами (рабочими, насосами, механизмами и т. п.). Объём работы в таких задачах обычно не указывается и не является искомым, а также предполагается, что выполняемая работа проводиться равномерно, т. е. с постоянной производительностью для каждого субъекта.  

В задачах на работу, системы уравнений содержат следующие величины:

·                      – время выполнения работы;

·                      – производительность, т. е. работа, производимая за единицу времени.  

·                      – работа, выполняемая за данное время.

Эти три величины связаны соотношением 

Обычно величина выполняемой работы нас не интересует, поэтому удобнее принимать объём всей работы за единицу, т. е. .

Исследуя прототипы из Открытого Банка задач ЕГЭ по математике на движение и производительность, нельзя не заметить, что все задачи данного типа можно разделить на две группы – задачи на «детали»  и задачи на «трубы». Для каждой из них составим  общие модели решения типовых задач, которые знать будет очень полезно.

В задачах «на детали» за неизвестные, как правило, надо принимать производительность – её роль такова же, как роль скорости в задачах на движение.

Правила решения задач на работу очень просты.

1. 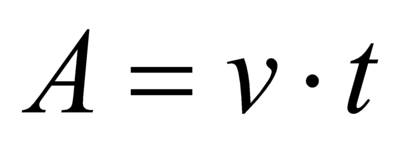                 , то есть работа= производительность  время. Из этой формулы легко найти t или v

2.                  .

3.                  Если объем работы не важен в задаче и нет никаких данных, позволяющих его найти — работа принимается за единицу. Заполнен  бассейн (один). Построено  здание (одно). А вот если речь идет о количестве кирпичей, воды или деталей — работа как раз и равна этому количеству.

4.                  Если трудятся двое  и более объектов  (два экскаватора, два завода…) — их производительности складываются.

5.                  В качестве переменной  удобно взять именно производительность.

Рассмотрим  применение  алгебраического метода  решения таких задач на практике.

Задача.  На изготовление 16 деталей первый мастер затрачивает на 6 часов меньше, чем второй мастер на изготовление 40 таких же деталей. Известно, что первый за час делает на 3 детали больше, чем второй. Сколько деталей в час делает второй мастер?

1 способ. Примем за х время работы одного из мастеров.

Решение:

Пусть  часов затрачивает второй мастер на изготовление 40 деталей. По условию задачи составим таблицу.

	Работа (детали)	Производительность (дет/час)	Время, (ч)
Первый  мастер	16
Второй  мастер	40

 

Зная, что первый мастер за час делает на 3 детали больше, чем второй, составим и решим уравнение.

Таким образом, второй мастер делает 40:8=5 деталей в час.

Ответ: 5 деталей в час.

2 способ. Примем за х производительность одного из рабочих.

 Решение:

Пусть  деталей в час делает второй мастер, где  По условию задачи, составим таблицу.

	Работа, (детали)	Производительность, (дет/час)	Время, (ч)
Первый мастер	16
Второй мастер	40

Зная, что первый мастер на выполнение работы затрачивает на 6 часов меньше, чем второй мастер, составим и решим уравнение.

Таким образом, второй мастер делает 5 деталей в час.

Ответ: 5 деталей в час.

Из приведенных решений видно, что выбор неизвестных не влияет на ответ задачи, но от этого зависит длина решения. Поэтому при решении задачи,  выбирать неизвестные стоит исходя из условия. Чем меньше действий предстоит совершить, тем быстрее решается  задача. А это очень большое преимущество на экзамене.

В задачах «на трубы»  модель решения схожа с задачами «на работу». Разница лишь в том, что здесь производительность трубы – это объём жидкости, протекающей через неё за единицу времени. Иногда в подобных задачах за неизвестные необходимо одновременно принять и объём бассейна, производительность труб, время наполнения и слива бассейна каждой трубой. Из-за большого количества неизвестных задача на первый взгляд может показаться очень трудной и нерешаемой, но это не так. Рассмотрим пример решения задачи.

Решая задачи «на работу», нужно  принимать за неизвестные величины производительность (работа, производимая за единицу времени), но бывают и исключения, где необходимо за неизвестную, например, выбрать время. Иногда встречаются такие задачи, в которых не указывается, какая работа выполняется. В таких задачах, будет удобнее ввести самим единицу работы, равную всей работе.

В заключении можно сделать некоторые выводы и дать рекомендации, которые необходимо знать при сдаче ЕГЭ.

При решении любых текстовых задач нужно обращать особое внимание на единицы измерения – в течение всего решения они обязательно должны быть одинаковыми.

Для преобразования условия задачи в математическую модель математические знания практически не нужны – необходим здравый смысл. Очень важно обязательно сформулировать, используя переменные, что необходимо найти, т. к. переменных может быть намного больше, чем уравнений, где все их найти просто невозможно.

Решая уравнения нужно помнить, что в текстовых задачах все величины, как правило, положительны, т. к. в природе отрицательных скоростей и расстояний не существует. Это даёт право на умножение, деление и на возведение в квадрат получающиеся уравнения и неравенства.

Решая задачи «на работу», очень выгодно принимать за неизвестные величины производительность (работа, производимая за единицу времени), но бывают и исключения, где необходимо за неизвестную, например, выбрать время. Иногда встречаются такие задачи, в которых не указывается, какая работа выполняется. В таких задачах, будет удобнее ввести самим единицу работы, равную всей работе.

 

Текстовые задачи.

1)Автомобиль расходует 9 литров бензина на 100 километров пути, а цена бензина — 26 рублей за литр. Сколько рублей потратил автомобилист на путь длиной 2600 км? Ответ: 6084

2)Стоимость проезда в автобусе 15 рублей, студент Миша каждый день ездит в институт и домой без пересадок на автобусе. Стоимость проезда за 1 день составляет 3% всей его стипендии. Какова его стипендия? Ответ: 1000

3)Килограмм персиков стоит 85 рублей. Сергей купил 3 кг персиков. Сколько рублей сдачи получил Сергей с 300 рублей? Ответ: 45

4)ЕГЭ по русскому языку сдали 92% выпускников, что составляет 23 выпускника. Сколько выпускников в школе не сдали ЕГЭ по русскому языку? Ответ: 2

5)Килограмм яблок стоит 55 рублей. Сколько рублей сдачи получит хозяйка с 500 рублей, если она купила 9 кг яблок? Ответ: 5

6)Электричка находится в пути между двумя пунктами 1 час 15 минут. Найдите, какой процент составляет это время от общего времени пути, которое составляет 6 часов 15 минут. Ответ: 20

7)Килограммовая пачка гречки стоит 27 рублей. Какое наибольшее коли­чество пачек гречки можно купить на 150 рублей? Ответ: 5

8)Строительной фирме нужно приобрести 75 м3. Бетона, однако она приобрела лишь треть нужного. Сколько бетона не хватило до нужного количества? Ответ: 50

9)Цветок лилии стоит 150 рублей. Дима купил букет из нескольких лилий для своей мамы. Сколько рублей потратил Дима, если он купил, нечётное количество лилий и у него было 800 рублей? Ответ: 5

10)Маршрутное такси за месяц проезжает 10000 км. Стоимость одного литра бензина 34,5 рубля. Средний расход бензина на 100 км — 13 лит­ров. Сколько рублей сдачи получит водитель с 4 000 рублей, если он купит 110 л? Ответ: 205

11)Цена ноутбука с 15%-ной скидкой — 25 500 рублей. Найдите цену ноутбука без скидки? Ответ: 29 325

12)Рабочие прокладывают дорогу длиной 12,6 км. Ежедневно они укла­дывают 800 м дороги. Какое наименьшее количество дней необходимо рабочим для прокладывания всей дороги? Ответ: 16

13)Для ремонта квартиры требуется 59 рулонов обоев. Сколько пачек обойного клея необходимо купить, если одна пачка клея предназначен на 9 рулонов? Ответ: 7

14)Стоимость покупки электроэнергии — 1 руб. 14 коп. за 1 кВт/ч, услуги по передаче — 1 руб. 82 коп. за 1 кВт/ч и иные услуги 13 коп. за 1 кВт/ч, потребление электричества в месяц составил 294 кВт/ч. Сколько рублей нужно заплатить за электричество за этот месяц? Ответ: 908,46

15)Стоимость купона на месяц 1700 рублей, а стоимость одной поездки — 60 рублей. Школьник приобретал билет каждую поездку, он сделал за месяц 34 поездки. Сколько рублей сэкономил школьник, если бы купил купон? Ответ: 340

16)В магазине «Сделай сам» мебель продаётся в разобранном виде. Покупатель может заказать сборку мебели на дом, стоимость сборки составляет 20% от стоимости самой мебели. Сколько рублей будет стоить компьютерный стол вместе со сборкой, если без сборки он стоит 4000 руб.? Ответ: 4800

17)Цена на холодильник была повышена на 12% и составила 14 000 рублей. Сколько рублей стоил холодильник до повышения цены? Ответ: 12500

18)Розничная цена учебника 156 рублей, она на 30% выше оптовой цены. Какое наибольшее число таких учебников можно купить по оптовой цене на 5000 рублей? Ответ: 41

19)Футболка стоила 600 рублей. После снижения цены она стала стоить 330 рублей. На сколько процентов была снижена цена на футболку? Ответ: 45

20)Магазин, делая наценку 50%, продает канцелярские наборы по цене 90 рублей за штуку. Какое наибольшее число таких наборов может закупить хозяин этого магазина на 4300 рублей? Ответ: 71

21)Магазин покупает чайники по оптовой цене 420 рублей за штуку, а продает с наценкой 25%. Какое наибольшее число таких чайников можно купить в этом магазине за 3400 рублей? Ответ: 6

22)Магазин делает пенсионерам скидку на определенное количество процентов от цены покупки. Пакет кефира в магазине стоит 45 рублей. Пенсионер заплатил за пакет кефира 41 рубль 40 копеек. Сколько процентов составляет скидка для пенсионеров? Ответ: 8

23)Среди 50000 жителей города 70% не интересуются футболом. Среди интересующихся 60% смотрели по телевизору финал Лиги чемпионов. Сколько жителей города смотрели этот матч? Ответ: 9000

24)В школе 1200 учеников, из них 16 февраля 5% отсутствовало на занятиях. Среди присутствовавших на занятиях учеников 40% обедало в школьной столовой. Сколько учеников обедали в школьной столовой в этот день? Ответ: 456

25)В некотором городе живет 300000 жителей, среди них 20% детей и подростков. Среди взрослых жителей 40% не работает (пенсионеры, студенты, домохозяйки и т.п.). Сколько взрослых жителей работает? Ответ: 144000

26)Футболка стоила 800 рублей. Затем цена была снижена на 15%. Сколько рублей сдачи с 1000 рублей должен получить покупатель при покупке этой футболки после снижения цены? Ответ: 320

27)Поезд отправился из Санкт – Петербурга в 23 часа 50 минут и прибыл в Москву в 7 часов 50 минут следующих суток. Сколько часов поезд находился в пути? Ответ: 8

28)Цена на товар была повышена на 16% и составила 348 рублей. Сколько рублей стоил товар до повышения цены? Ответ: 300

29)В супермаркете проходит рекламная акция: покупая две шоколадки, покупатель получает третью шоколадку в подарок. Шоколадка стоит 35 руб. Какое наибольшее число шоколадок можно получить за 200 руб.? Ответ: 7

30)Поезд Санкт-Петербург – Нижний Новгород отправляется в 17.30, а прибывает в 8.30 следующего дня (время московское). Сколько часов поезд находится в пути? Ответ: 15

31)Хозяин овощной лавки купил на оптовом рынке 100кг помидоров и заплатил 4000 рублей. После продажи помидоров оказалось, что за время хранения в лавке 10% помидоров испортились, и хозяин не смог их продать. Остальные помидоры он продал по цене 50 руб. за килограмм. Какую прибыль он получил? Ответ: 500

32)В книге Елены Молоховец “Подарок молодым хозяйкам” имеется рецепт пирога с черносливом. Для пирога на 9 человек, кроме всего прочего, следует взять 0,3 фунта чернослива. Сколько граммов чернослива следует взять для пирога, рассчитанного на 12 человек? Считайте, что 1 фунт равен 0,4 кг. Ответ: 160

33)Диагональ экрана телевизора равна 24 дюймам. Выразите диагональ экрана в сантиметрах, если в одном дюйме 2,54 см. Результат округлите до целого числа сантиметров. Ответ: 61

34)Бегун пробежал 800м. за 2 минуты 40 секунд. Найдите среднюю скорость бегуна на дистанции. Ответ дайте в км/час. Ответ: 18

35)Диагональ экрана телевизора равна 43 дюймам. Выразите диагональ экрана в сантиметрах, если в одном дюйме 2,54 см. Результат округлите до целого числа сантиметров.

36)В розницу один номер еженедельного журнала “Репортаж” стоит 27руб., а полугодовая подписка на этот журнал стоит 550руб. За полгода выходит 25 номеров журнала. Сколько рублей сэкономит г-н Иванов за полгода, если не будет покупать каждый номер журнала отдельно, а оформит подписку? Ответ: 125

37)Теплоход рассчитан на 650 пассажиров и 20 членов команды. Каждая спасательная шлюпка может вместить 70 человек. Какое наименьшее число шлюпок должно быть на теплоходе, чтобы в случае необходимости в них можно было разместить всех пассажиров и всех членов команды? Ответ: 10

38)Наташе надо изготовить 300 бумажных журавликов. Ежедневно она делает на одно и то же количество журавликов больше по сравнению с предыдущим днём. В первый день Наташа сделала 6 журавликов. Сколько журавликов было сделано в последний день, если на всю работу потребовалось 15 дней? Ответ: 34

39)Два велосипедиста одновременно отправились из деревни A в деревню B, расстояние между которыми 21 км. Скорость первого велосипедиста была на 3 км/ч больше скорости второго велосипедиста. Найдите скорость второго велосипедиста, если он приехал в деревню B на 10 мин позже первого. Ответ дайте в км/ч. Ответ: 18

40)Коле надо посадить 350 кустов роз. Ежедневно он сажает на одно и то же количество кустов больше по сравнению с предыдущим днём. В первый день он посадил 8 кустов роз. Сколько кустов было посажено в последний день, если на всю работу потребовалось 20 дней? Ответ: 27

41)Обе трубы наполняют бассейн за 6 часов, а первая труба — за 10 часов. За сколько часов наполнит бассейн вторая труба? Ответ: 15

42)Первая труба пропускает на 2 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если ёмкость объёмом 420 литров она заполняет на 15 минут дольше, чем вторая труба заполняет ёмкость объёмом 280 литров? Ответ: 12

43)Моторная лодка прошла против течения реки 160 км и вернулась в пункт отправления, затратив на обратный путь на 8 часов меньше времени. Известно, что в неподвижной воде лодка движется со скоростью 15 км/ч. Найдите скорость течения реки. Ответ: 5

44)Два мотоциклиста выехали одновременно из города A в город B, расстояние между которыми 171 км. За один час первый мотоциклист проезжает расстояние на 40 км больше второго мотоциклиста. Найдите скорость второго мотоциклиста, если он приехал в пункт В на 2,5 часа позже первого. Ответ дайте в км/ч. Ответ: 36

45)Елена сделала вклад в банк в размере 5500 рублей. Проценты по вкладу начисляются раз в год и прибавляются к текущей сумме вклада. Спустя год Наталья положила такую же сумму в этот же банк и на тех же условиях. Ещё через год Елена и Наталья одновременно закрыли вклады и забрали деньги. В результате Елена получила на 739,2 рубля больше, чем получила Наталья. Найдите, какой процент годовых начислял банк по вкладам? Ответ: 12

46)Предприниматель Петров получил в 2005 году прибыль в размере 12\,00012000 рублей. Каждый следующий год его прибыль увеличивалась на 110\%110% по сравнению с предыдущим годом. Сколько рублей заработал Петров за 2008 год? Ответ: 111132

47)Имеется два сплава. Первый сплав содержит 12\%12% железа, второй — 28\%28% железа. Масса второго сплава больше массы первого на 2 кг. Из этих двух сплавов изготовили третий сплав с содержанием железа 21\%21%. Найдите массу третьего сплава. Ответ дайте в килограммах. Ответ: 16

48)По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 80 км/ч и 50 км/ч. Товарный поезд имеет длину 1100 метров. Какова длина пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 3 минуты 6 секунд. Ответ дайте в метрах. Ответ: 450

49)Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо семафора за 45 секунд. Найдите длину поезда в метрах. Ответ: 750

50)Поезд, двигаясь равномерно со скоростью 63 км/ч, проезжает мимо здания вокзала, длина которого равна 150 метров, за 1 минуту. Найдите длину поезда в метрах. Ответ: 900

51)Из двух посёлков, расстояние между которыми 88 км, навстречу друг другу одновременно выехали два велосипедиста. Через сколько часов велосипедисты встретятся, если их скорости равны 18 км/ч и 22 км/ч? Ответ: 2,2

52)Один рабочий может выполнить заказ за 9 часов, другой — за 6 часов. За сколько часов выполнят весь заказ оба рабочих вместе? Ответ: 3,6

53)Заказ на 180 деталей первый рабочий выполняет на 3 часа быстрее, чем второй. Сколько деталей в час изготавливает второй рабочий, если первый за час успевает сделать на 2 детали больше? Ответ: 10

54)Теплоход проходит по течению реки до пункта назначения 221 км и после стоянки возвращается в пункт отправления. Скорость движения теплохода в воде без течения равна 15 км/ч. Стоянка длилась 7 часов. Найдите скорость течения реки, если в пункт отправления теплоход вернулся через 37 часов после отплытия из него. Ответ дайте в км/ч. Ответ: 2

55)Велосипедист выехал с постоянной скоростью из города A в город B, расстояние между которыми 288 км. На следующий день он поехал обратно со скоростью на 6 км/ч больше прежней. По пути велосипедист останавливался и отдыхал 4 часа. В итоге на возвращение в город A у него ушло сколько же времени, сколько на путь из A в B. Найдите скорость велосипедиста на пути из A в B. Ответ дайте в км/ч. Ответ: 18

56)Из пункта A в пункт B одновременно выехали две дорожные машины. Первая машина проехала с постоянной скоростью весь путь. Вторая проехала первую половину пути со скоростью 39 км/ч, а вторую половину пути — со скоростью на 26 км/ч большей скорости первой машины, в результате чего в пункт B обе машины прибыли одновременно. Найдите скорость первой машины. Ответ дайте в км/ч. Ответ: 52

57)Цена телевизора в магазине ежеквартально (в квартале — три месяца) уменьшается на одно и то же число процентов от предыдущей цены. Известно, что телевизор, стоимостью 50 000 рублей был продан спустя два квартала за 41 405 рублей. Найдите, на сколько процентов ежеквартально уменьшалась стоимость телевизора. Ответ: 9

58)В 2005 году в посёлке проживало 55 000 человек. В 2006 году, в результате строительства новых домов, число жителей увеличилось на 6%, а в 2007 году — на 10% по отношению к 2006 году. Найдите, число жителей посёлка в 2007 году. Ответ: 64130

59)В сосуд, содержащий 3 литра 14-процентного водного раствора некоторого вещества, добавили 4 литра воды. Найдите концентрацию (в процентах) получившегося после смешивания раствора. Ответ: 6

60)Из одной точки круговой трассы, длина которой 18 км, одновременно в одном направлении стартовали два автомобиля. Спустя 40 минут после начала движения, один автомобиль опередил второй ровно на один круг. Найдите скорость второго автомобиля, если скорость первого равна 90 км/ч. Ответ дайте в км/ч. Ответ: 63

61)Из двух городов, расстояние между которыми равно 544 км, навстречу друг другу одновременно выехали два автомобиля. Скорости движения автомобилей равны 64 км/ч и 72 км/ч. Через сколько часов автомобили встретятся? Ответ: 4

62)По морю параллельными курсами в одном направлении следуют два сухогруза: первый имеет длину 105 метров, второй — 100 метров. Первый сухогруз обходит второго и в определенный момент времени расстояние от носа второго сухогруза до кормы первого равно 500 метров. Спустя 13 минут второй сухогруз обходит первого, и этот момент времени расстояние от носа первого сухогруза до кормы второго составило 400 метров. Определите, на сколько скорость первого сухогруза меньше скорости второго? Ответ дайте в километрах в час. Ответ: 5, 1

63)Плиточник должен уложить 320 м² плитки. Если он будет укладывать на 6 м² в день больше, чем запланировал, то работа будет выполнена на 12 дней раньше. Определите, сколько квадратных метров плитки в день планирует укладывать плиточник. Ответ: 10

64)Грузовой автомобиль перевозит технику из одного города в другой, проезжая в каждый последующий день на одно и то же расстояние больше, чем в предыдущий день. В первый день пути водитель проехал расстояние 520 км. Известно, что расстояние между городами 3270 км и на весь путь потребовалось ровно 5 дней. Определите, сколько километров проехал водитель за третий день пути. Ответ: 654

65)Ремонт одной и той же квартиры Виктор и Алексей делают за 8 дней. Андрей, работая с Виктором, затрачивают на работу столько же времени. Однако, Андрею с Алексеем на ремонт требуется 12 дней. Сколько дней займет ремонт квартиры при одновременной работе всех трех мастеров? Ответ: 6

66)Два маляра могут выполнить работу по покраске стен помещения за 15 дней, а первый из них в одиночку — за 20 дней. Сколько дней необходимо второму маляру, чтобы выполнить работу самостоятельно? Ответ: 60

67)Мотоциклист проехал расстояние в 180 км от A до B с постоянной скоростью. На следующий день он проехал это же расстояние в обратную сторону из B в A со скоростью на 10 км/ч меньше прежней. Возвращаясь, он сделал остановку на 24 минуты и в итоге на дорогу из B в A ушло времени на 1 час больше, чем в прошлый раз на путь из A в B. Найдите скорость мотоциклиста на пути из A и B. Ответ дайте в км/ч. Ответ: 60

68)Строительные фирмы учредили компанию с уставным капиталом 150 млн рублей. Первая фирма внесла 20% уставного капитала, вторая фирма — 22,5 млн рублей, третья — 0,3 уставного капитала, четвертая фирма внесла оставшуюся часть. По договоренности ежегодная прибыль между фирмами будет расформирована пропорционально внесенным в уставный капитал вкладам. Какую сумму получит четвертая фирма, если прибыль составила 100 млн рублей? Ответ дайте в млн рублей. Ответ: 35

69)В результате смешивания 25%-го и 15%-го растворов серной кислоты было получено 750 г 20%-го раствора. Сколько граммов 15%-го раствора было использовано? Ответ: 375

70)Из городов A и B, расстояние между которыми 270 км, одновременно навстречу друг другу выехали два автобуса. Они встретились спустя 2,5 часа после начала движения на расстоянии 140 км от города A. С какой скоростью двигался автобус, выехавший из города B. Ответ дайте к км/час. Ответ: 52

71)Имеются два куска металла массой 80 г и 70 г, которые содержат различную концентрацию серебра. Если сплавить эти два металла, то на выходе получится металл, который будет содержать 63% серебра. Если же сплавить одинаковые массы этих металлов, то результатом будет сплав, содержащий 65% серебра. Найдите, сколько граммов серебра находится в первом куске металла. Ответ: 28

72)Первый рабочий обтачивает на токарном станке на 1 заготовку в день меньше, чем второй. При этом известно, что на обработку 420 деталей ему потребуется на 9 дней больше, чем второму на обтачивание 252 деталей. Определите, сколько деталей в день способен обточить второй рабочий. Ответ: 21

73)В финальном заезде гонки участвовали два гонщика. Заезд проводился на кольцевой трассе, имеющей протяженность 6 км. Гонщикам было необходимо проехать 68 кругов. В результате первый гонщик пришел на финиш раньше второго на 15 минут. Найдите среднюю скорость второго гонщика, если известно, что он отстал от первого ровно на круг через 60 минут после начала гонки, а стартовали они одновременно. Ответ выразите в км/ч. Ответ: 96

74)Оля и Витя начали одновременно решать одинаковый тест. За один час Оля успевает решать 12 вопросов, а Витя 21 вопрос. Оля закончила решать тест на 105 минут позже Вити. Определите количество вопросов в тесте. Ответ: 49

75)Города A и B расположены на расстоянии 630 км друг от друга. Из города A в город B выехал мотоциклист. Спустя 3 часа навстречу ему из города B по тому же маршруту выехал автомобиль. Найдите скорость мотоциклиста, если скорость автомобиля составляла 70 км/ч., а встретились они на расстоянии 350 км от города А. Ответ: 50

76)Через первую трубу в бассейн попадает на 8 литров воды в минуту меньше, чем через вторую. Определите, сколько первая труба пропускает литров в минуту, если она заполняет бассейн объемом 180 литров на 8 минут дольше второй.Через первую трубу в бассейн попадает на 8 литров воды в минуту меньше, чем через вторую. Определите, сколько первая труба пропускает литров в минуту, если она заполняет бассейн объемом 180 литров на 8 минут дольше второй. Ответ: 10

77)В двух сплавах имеется различное содержание кобальта. В первом – 25%, во втором – 30% кобальта. На производстве из них был получен третий сплав общей массой 150 кг, в котором содержится 28% кобальта. Определите разницу в весе двух сплавов. Ответ дайте в килограммах. Ответ: 30

78)От станции А к станции В с постоянной скоростью отправился первый поезд. Расстояние между станциями составляет 153 км. Спустя 8 часов после отправления первого поезда, по тому же маршруту выехал второй поезд. Его скорость на 8 км/ч больше, чем у первого. С какой скоростью двигался первый поезд, если на конечную станцию оба поезда прибыли одновременно. Ответ дайте в км/ч. Ответ: 9

79)Один мастер делает 25 деталей в час, а другой 35 деталей в час. Сколько деталей сделает второй мастер, пока первый сделает 100 деталей?

80)Один мастер может выполнить заказ за 12 часов, а другой за 6 часов. За сколько часов выполнят заказ оба мастера, работая вместе?

81)Дима и Саша выполняют одинаковый тест. Дима отвечает за час на 12 вопросов теста, а Саша — на 22. Они одновременно начали отвечать на вопросы теста, и Дима закончил свой тест позже Саши на 75 минут. Сколько вопросов содержит тест?

82)На изготовление 231 детали ученик тратит на 11 часов больше, чем мастер на изготовление 462 таких же деталей. Известно, что ученик за час делает на 4 детали меньше, чем мастер. Сколько деталей в час делает ученик?

83)Две трубы наполняют бассейн за 3 часа 36 минут, а одна первая труба наполняет бассейн за 6 часов. За сколько часов наполняет бассейн одна вторая труба?

84)Игорь и Паша красят забор за 9 часов. Паша и Володя красят этот же забор за 12 часов, а Володя и Игорь – за 18 часов. За сколько часов мальчики покрасят забор, работая втроем?

85)Двое рабочих, работая вместе, могут выполнить работу за 12 дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за два дня выполняет такую же часть работы, какую второй – за три дня?

86)Две бригады, состоящие из рабочих одинаковой квалификации, одновременно начали выполнять два одинаковых заказа. В первой бригаде было 16 рабочих, а во второй — 25 рабочих. Через 7 дней после начала работы в первую бригаду перешли 8 рабочих из второй бригады. В итоге оба заказа были выполнены одновременно. Найдите, сколько дней потребовалось на выполнение заказов.

87)Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?

88)Имеется два сплава. Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

89)Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?

90)Имеются два сосуда. Первый содержит 30 кг, а второй – 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?

91)В сосуд, содержащий 5 литров 12–процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?

92)Смешали 4 литра 15–процентного водного раствора некоторого вещества с 6 литрами 25–процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

93)Смешали некоторое количество 15–процентного раствора некоторого вещества с таким же количеством 19–процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?

94)Моторная лодка прошла 36 км по течению реки и вернулась обратно, потратив на весь путь 5 часов. Скорость течения реки равна 3 км/ч. Найдите скорость лодки в неподвижной воде.

95)Рыболов в 5 часов утра на моторной лодке отправился от пристани против течения реки, через некоторое время бросил якорь, 2 часа ловил рыбу и вернулся обратно в 10 часов утра того же дня. На какое расстояние от пристани он отдалился, если скорость реки равна 2 км/ч, а собственная скорость лодки 6 км/ч?

96)Катер прошёл от одной пристани до другой, расстояние между которыми по реке равно 48 км, сделал стоянку на 20 мин и вернулся обратно через 5 1/3 ч после начала поездки. Найдите скорость течения реки, если известно, что скорость катера в стоячей воде равна 20 км/ч.

97)Расстояние между пристанями А и В равно 126 км. Из А в В по течению реки отправился плот, а через 1 час вслед за ним отправилась яхта, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот прошел 34 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в км/ч.

98)Из пункта А в пункт В, расположенный ниже по течению реки, отправился плот. Одновременно навстречу ему из пункта В вышел катер. Встретив плот, катер сразу повернул и поплыл назад. Какую часть пути от А до В пройдет плот к моменту возвращения катера в пункт В, если скорость катера в стоячей воде вчетверо больше скорости течения реки?

99)Пристани A и B расположены на реке, скорость течения которой на этом участке равна 3 км/ч. Лодка проходит туда и обратно без остановок со средней скоростью 8 км/ч. Найдите собственную скорость лодки.

100)Четыре бригады должны разгрузить вагон с продуктами. Вторая, третья и четвёртая бригады вместе могут выполнить эту работу за 4 часа, первая, третья и четвёртая – за 3 часа. Если же будут работать только первая и вторая бригады, то вагон будет разгружен за 6 часов. За какое время могут разгрузить вагон все четыре бригады, работая вместе?