Тема. Практическая работа №11" Решение задач с использованием процедур и функций". Инструктаж по ТБ.

Инструкция к практической работе №11

Тема: Решение задач с использованием процедур и функций.

Цель: повторить основные правила языка программирования, сформировать умения выполнения действий в среде программирования Pascal.ABC.net. Оборудование: ПК, проектор, учебник, тетрадь

Ход урока

      I.            Инструктаж по ТБ

   II.            Задания для практической работы

Наберите и выполните программы

 ВАРИАНТЫ ЗАДАНИЙ

Задание 1

Для решения всех задач сделать два варианта программы: с реализацией указанной подпрограммы в виде функции и в виде процедуры. 

Уровень 1

1. Составить программу нахождения наибольшего общего делителя (НОД) и наименьшего общего кратного (НОК) двух натуральных чисел

.

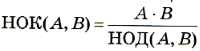Использовать подпрограмму алгоритма Евклида для определения НОД.

2. Вычислить площадь правильного шестиугольника со стороной а, используя подпрограмму вычисления площади треугольника.

3. Даны две дроби  — (А, В, С, D — натуральные числа).

Составить программу деления дроби на дробь. Ответ должен быть несократимой дробью. Использовать подпрограмму алгоритма Евклида для определения НОД.

4. Даны две дроби  — (А, В, С, D — натуральные числа).

Составить программу умножения дроби на дробь. Ответ должен быть несократимой дробью. Использовать подпрограмму алгоритма Евклида для определения НОД.

5. Даны две дроби  — (А, В, С, D — натуральные числа).

Составить программу вычитания из первой дроби второй. Ответ должен быть несократимой дробью. Использовать подпрограмму алгоритма Евклида для определения НОД.

6. Написать программу вычисления суммы  — для заданного числа n. Результат представить в виде несократимой дроби  (р, q — натуральные). Использовать подпрограммы алгоритма Евклида для определения НОД и сложения двух простых дробей.

7. Даны числа X, Y, Z, Т — длины сторон четырехугольника. Вычислить его площадь, если угол между сторонами длиной X и Y — прямой. Использовать две подпрограммы для вычисления площадей: прямоугольного треугольника и прямоугольника. 

Задание 2

Для всех задач выделить подзадачи, решения которых могут быть реализованы через подпрограммы. Выбрать наиболее удобный вариант подпрограммы: функцию или процедуру. Составить программу решения задачи. 

Уровень 2

1. Дано простое число. Найти следующее за ним простое число.

2. Для заданного натурального числа п найти наименьший нечетный натуральный делитель k (k ≠ 1).

3. Заменить данное натуральное число на число, которое получается из исходного записью его цифр в обратном порядке (например, дано число 156, нужно получить 651).

4. Найти все натуральные числа, не превосходящие заданного п, которые делятся на каждую из своих цифр.

5. Имеется часть катушки с автобусными билетами. Номер билета шестизначный. Составить программу, определяющую количество счастливых билетов на катушке, если меньший номер билета — N, больший — М (билет является счастливым, если сумма первых трех его цифр равна сумме последних трех).

6. Из заданного числа вычли сумму его цифр. Из результата вновь вычли сумму его цифр и т. д. Через сколько таких действий получится нуль?

7. На отрезке [100, А] (2¹⁰ < N < 2³¹) найти количество чисел, составленных из цифр а, b, с.

8. Найти все натуральные n-значные числа, цифры в которых образуют строго возрастающую последовательность (например, 1234,5789). 

Уровень 3

9. Два простых числа называются «близнецами», если они отличаются друг от друга на 2 (например, 41 и 43). Напечатать все пары «близнецов» из отрезка [n, 2n], где n — заданное натуральное число, большее 2.

10. Дано четное число n > 2. Проверить для него гипотезу Гольдбаха: каждое четное п представляется в виде суммы двух простых чисел.

11. Составить программу разложения данного натурального числа на простые множители. Например, 200 = 2³ • 5².

12. Дано натуральное число n. Найти все меньшие п числа Мерсенна. (Простое число называется числом Мерсенна, если оно может быть представлено в виде 2^p — 1, где р — тоже простое число. Например, 31 = 2⁵ - 1 — число Мерсенна.)

13. Два натуральных числа называются «дружественными», если каждое из них равно сумме всех делителей (кроме его самого) другого (например, числа 220 и 284). Найти все пары «дружественных» чисел, которые не больше данного числа N.

14. Натуральное число, в записи которого n цифр, называется числом Армстронга, если сумма его цифр, возведенная в степень n, равна самому числу. Найти все числа Армстронга от 1 до k.

15. Найти все простые натуральные числа, не превосходящие n, двоичная запись которых представляет собой палиндром, т. е. читается одинаково слева направо и справа налево.

16. Составить программу для нахождения чисел из интервала [М, N], имеющих наибольшее количество делителей.

17 Дано натуральное число n > 1. Определить длину периода десятичной записи дроби 1/n. 

III.            Алгоритм выполнения (Краткие теоретические сведения)

1.     Запустите программу Pascal.ABC.net

2.     Изучите окно программы

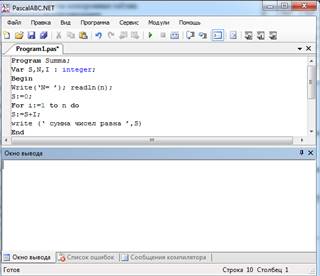
3.     Введите текст программы. При наборе не стоит учитывать регистр вводимых символов. В Pascal нет различий между заглавными и строчными буквами.

4.     Запустите программу на компиляцию. С помощью клавиши F5 или кнопкой запуска программы.

5.     Если программа набрана без ошибок, то в ОКНЕ ВЫВОДА  вы увидите приглашение ввести данные.

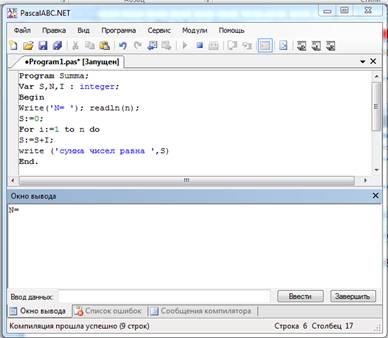
6.     После ввода данных необходимо нажать клавишу ENTER

7.     Если в программе имеются логические, грамматические, синтаксические ошибки, то вы увидите сообщение об ошибке программы.

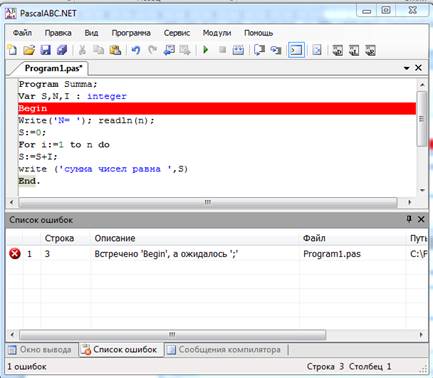
Толкование ошибки – в строке предшествующей строке BEGIN пропущен знак « ; ».

8.     После компиляции  протестируйте программу.

a.      Запустите программу  на выполнение

b.     Введите тестовые данные

c.      Сверьте ответ, если ответы совпали, программу можно считать правильной.

Пример

В Паскале различаются две разновидности подпрограмм: процедуры и функции. Рассмотрим этот вопрос на примере следующей задачи: даны два натуральных числа а и b. Требуется определить наибольший общий делитель трех величин: а + b, а² + b², а • b.

Запишем это так: НОД(а + b, а² + b², а • b).

Идея решения состоит в следующем математическом факте: если х, у, z — три натуральных числа, то НОД(х, y, z) = НОД(НОД(х, у), z). Иначе говоря, нужно найти НОД двух величин, а затем НОД полученного значения и третьего числа (попробуйте это доказать).

Очевидно, что вспомогательным алгоритмом для решения поставленной задачи является алгоритм получения наибольшего общего делителя двух чисел. Эта задача решается с помощью алгоритма Евклида, который подробно обсуждался в 9 классе. Напомним, что идея алгоритма Евклида основана на следующей формуле:

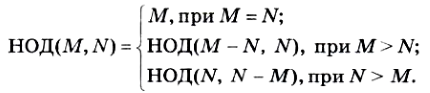
Приведем алгоритм решения поставленной задачи на учебном Алгоритмическом языке. Алгоритм состоит из процедуры «Евклид» и основного алгоритма «Задача», в котором присутствуют два обращения к процедуре:

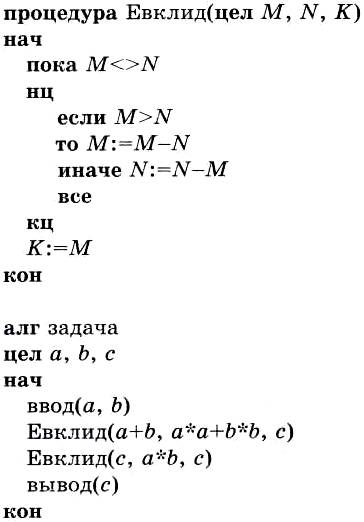
Здесь М, N и К являются формальными параметрами процедуры. М и N — параметры-аргументы, К — параметр-результат.

Процедуры в Паскале. Основное отличие процедур в Паскале от процедур в Алгоритмическом языке (АЯ) состоит в том, что процедуры в Паскале описываются в разделе описания подпрограмм, а в АЯ процедура является внешней по отношению к вызывающей программе. Теперь посмотрим, как решение поставленной задачи программируется на Паскале.

Теперь рассмотрим другой вариант программы, решающей ту же задачу. В ней используется процедура без параметров.

Программа решения рассмотренной выше задачи с использованием функции будет выглядеть следующим образом:

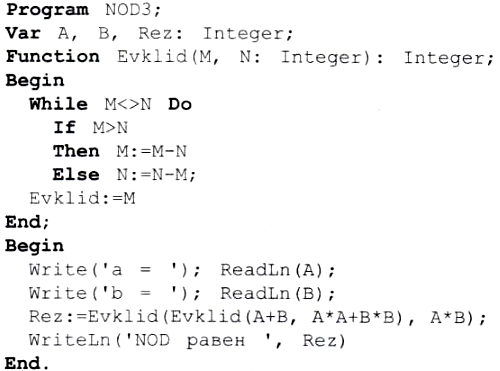
Из примера видно, что тело функции отличается от тела процедуры только тем, что в функции результат присваивается идентификатору функции:Evklid:=M.

IV.            Заполнение и сохранение файла- отчета о практической работе  в своей личной рабочей папке.

Отчет о практической работе № 11

Тема: Решение задач с использованием процедур и функций.

Цель: повторить основные правила языка программирования, сформировать умения выполнения действий в среде программирования Pascal.ABC.net.

Ход урока

       I.            Инструктаж по ТБ

    II.            Выполните задания. Напишите программу согласно заданию.

Вариант № ___

Уровень 1 __________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Уровень 2 __________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Уровень 3 __________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

 III.            Вывод: выполнив практическую работу я научился(лась), ____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

___________________________________________________________