Тема: Решение линейных уравнений с параметрами, составление схемы-алгоритма решения линейного уравнения с параметрами. Понятие «разветвленного уравнения»

Тема: Решение линейных уравнений с параметрами, составление схемы-алгоритма решения линейного уравнения с параметрами. Понятие «разветвленного уравнения»

Цель: сформировать умение решать линейные уравнения с параметрами по схеме-алгоритму; ввести понятие «разветвленного уравнения»; развивать исследовательские способы мышления, наблюдательность.

Ход занятия

I. Организационный этап

II. Актуализация опорных знаний и умений, проверка домашнего задания

1. Повторение теоретических сведений

1) Дайте определение линейного уравнения.

2) Какие вы знаете свойства линейных уравнений?

3) Сколько корней может иметь уравнение ax = b? Приведите примеры.

4) Сформулируйте определение параметра.

5) Сколько корней может иметь линейное уравнение с параметром? От чего это зависит? Приведите собственные примеры.

III. Изучение нового материала

Известно, что при решении линейного уравнения его сначала нужно свести к виду ax =b. Далее можно пользоваться таблицей свойств линейного уравнения. Можно эти же действия представить в виде схемы или алгоритма.

Решите уравнение относительно x:

1) 30x + a = 0.

Решение

3х + а = 0, 3х = - а.

Получили линейное уравнение, которе имеет единственный корень

 x = - а/3 при любых значениях параметра a.

Ответ. При любом значении a x = -а/3.

2) 8 – bx = - 1.

Решение

8 – bx = - 1,  - bx = - 9,  bx = 9.

Получили линейное уравнение. Определим, сколько корней имеет уравнение в зависимости от значений параметра b:

если  b = 0, то уравнение приобретает вид 0x = 9 и не имеет корней;

если b ≠ 0, то уравнение имеет единственный корень x = 9/b.

Ответ. При b = 0 корней нет; при b ≠ 0 x = 9/b.

3) kx + k  = 180.

Решение. Сведем уравнение к линейному:

kx + k  = 180, kx  = 180 – k.

Определим количество его корней в зависимости от параметра k:

если k = 0, то уравнение приобретает вид 0x =180 и корней не имеет;

если k ≠ 0, то уравнение имеет корень x= 180 – k/k.

Ответ. При k = 0 корней нет; при k ≠ 0 x = 180 – k/k.

Сделаем несколько обобщений.

1. Решить уравнение с параметрами означает:

1) указать значения параметров, при которых уравнение имеет корни (определить их количество при различных значениях параметров) или не имеет корней;

2) найти все выражения для корней уравнения и для каждого указать значения параметров.

2. При определенных значениях параметра (назовем их «контрольными») происходит качественное изменение уравнения и соответственно изменяется количество его корней.

3. Для линейных уравнений с параметром (и таких, которые сводят к линейным с помощью равносильных преобразований) «контрольными», как правило, являются такие значения параметра, которые превращаются в ноль при переменной. Итак, чтобы решить линейное уравнение с параметром, необходимо найти «контрольные» значения параметра, решить уравнения при этих «контрольных» значениях и при значениях, отличных от «контрольных».

4. Очень важно правильно записать ответ, особенно тогда, когда решение «разветвляется» в зависимости от значений параметра. Будем пользоваться такой формой записи: при «...» значениях параметра уравнение имеет корни «...»; при «...» значениях параметра уравнение не имеет корней. Подчеркнем, что решить уравнение с параметром значит найти все его решения для допустимых значений параметра (если условием задачи не ограничена область изменения параметра).

Например, ответ к некоторому уравнению с параметром (без ограничения области его изменения):

при x ≠ a/2  x = a + b не будет правильным. Почему? Поскольку при значении b = -a/2  x = a + b = a/2.

Тогда правильным будет ответ:

при b = -a/2 корней нет; при b ≠ -a/2  x = a + b.

Теперь составим схему-алгоритм для решения уравнений с параметром, которые можно свести к линейным.

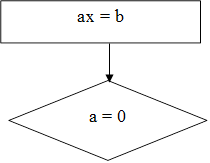                 нет (а ≠ 0)                                                да (а = 0)

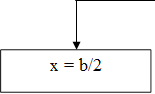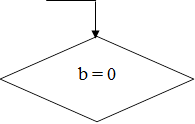Это исследование можно записать с помощью слов «если ..., то ...».

Например, исследования корней уравнения ax = b может выглядеть так:

1) Если a ≠ 0, то x = b/a;

2) если a = 0 и b ≠ 0, то корней нет;

3) если a = 0 и b = 0, то x - любое число.

Отметим, что линейное уравнение ax = b с определенным числовым значением b решают как имеющее один параметр - a. Если значение b также неизвестно, то в уравнении будет два разных параметра a и b. Уравнение может иметь и более двух параметров, обозначающие разными буквами.

IV. Закрепление новых знаний

1. Составьте схему для решения уравнения

(2 + m)x – 3 = 0

и решите его.

Решение.

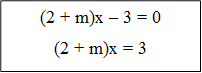Имеем

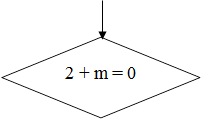                 нет                                                           да

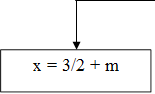1) Если 2  + m ≠ 0, то  m ≠ 2, то

х = 3 /2 + m;

2) если 2 + m = 0, то есть m = - 2, то корней нет.

Ответ. При m ≠ -2 x =  3/2 + m ; при m = -2 корней нет.

2. Составьте схему для решения уравнения

а² х – аb = а и решите его.

Решим следующие уравнения по алгоритму без построения схемы.

3. Решите уравнение ax  - 3 =  b в зависимости от параметров a и b.      Исправьте ошибки в ответах к уравнений с параметрами, которые решали относительно x:

1) при x ≠ 2 x =a + 3,

2) при x ≠ a x=a + b - 1;

3) при x ≠ b  x = a² b;

4) при x∉ {1;2}; x = a+ 1;

5) при x ≠ 3  x ∈ { a + 1; a - 1}.                                                  

V. Подведение итогов занятия

Фронтальная беседа

1. По какой схеме можно решить линейное уравнение с параметром?

2. Как правильно оформить запись ответа?

VI. Домашнее задание

1. Составить линейное уравнение с параметром и блок-схему к его решению.

2. Исправить ошибки в ответах к задачам с параметрами, которые решали относительно x:

1) при x ∉ {0;3}  x ∈  {а + 3;а};

2) при x ∉ {1;2}; x ∈ - {3;а - b};

3) при x ∉ {2;а}; x ∈  {а + b;0};

4) при x ∉  {-1;1}; x ∈  {а + 1; а²; 4}.

3. Решить уравнение 4 + bx = a относительно х.