Тема урока: Сложение натуральных чисел. Свойства сложения

Тема урока:

 Сложение натуральных чисел. Свойства сложения

Тип урока. Урок открытия новых знаний

Цель урока: Формирование способности учащихся к новому способу действия, расширение понятийной базы, применять полученные знания при выполнении сложения натуральных чисел.

Задачи урока:

Образовательные: - повторить понятия слагаемого, суммы;

- повторить свойства сложения;

- формировать умения использовать координатный луч для выполнения сложения натуральных чисел;

- формировать умения решать текстовые задачи.

Развивающие: -  развивать навыки сложения натуральных чисел, логическое мышление учащихся и речь, способность делать выводы;

– развивать у учащихся память и внимание

- развивать умение анализировать, сравнивать и делать выводы;

- развивать устную речь;

Воспитательные: - воспитывать умение высказывать свое мнение;

- воспитание умения участвовать в диалоге;

- формировать способность к позитивному сотрудничеству.

Задачи урока: вспомнить понятия слагаемое, сумма; свойства сложения закреплять и развивать навыки сложения натуральных чисел.

Ход урока

1. Мотивация к учебной деятельности

- организационный момент

а) Приветствие учащихся.

б) Мотивация к уроку – устный счёт. (Слайд 2)

Чтобы сложить числа 5 и 2, можно к числу 5 прибавить 1 и к полученному числу 6 еще раз прибавить 1. Имеем: 5 + 2 = 5 + 1 + 1 = 6 + 1 = 7. Но так вы складывали числа, когда учились в начальной школе. Сейчас, вы не задумываясь, по памяти пишите: 2 + 7 = 9, 6 + 3 = 9, 2 + 8 = 10, 8 + 7 = 15 и т.д., т.е. знаете наизусть таблицу сложения однозначных чисел.

Почему удобно складывать многозначные числа в столбик? Сложим, например, числа 3 853 164 и 2 700 503.

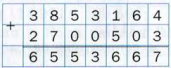
 При таом поразрядном сложении вычисления приходится проводить только с однозначными числами, что не вызывает затруднений.

Напомним, что в равенстве a + b = c числа a и b называют слагаемыми, число с и запись a + b − суммой. Здесь буквами обозначены числа.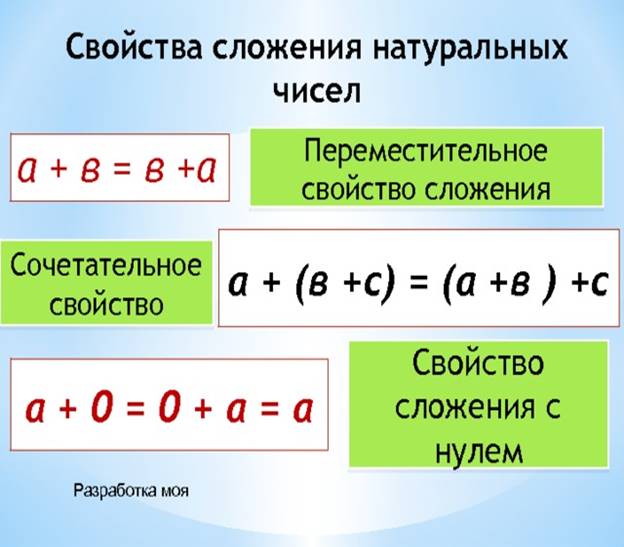

Вам хорошо известно переместительное свойство сложения.

От перестановки слагаемых сумма не меняется.

В буквенном виде это свойство записывают так:

a + b = b + a

Как удобнее вычислить сумму (64 + 23) + 77?

Скорее всего вы поступите так:

(64 + 23) + 77 = 64 + (23 + 77) = 64 + 100 = 164.

Здесь мы воспользовались сочетательным свойством сложения.

Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел.

В буквенном виде это свойство записываю так:

(a + b) + c = a + (b + c)

Из свойств сложения следует, что при сложении нескольких чисел слагаемые можно менять местами и заключать их в скобки, тем самым определяя порядок вычислений.

Например, верны равенства:

a + b + c = c + b + a,

2 + 3 + 7 + 8 = (2 + 8) + (7 + 3).

При сложении число 0 обладает особым свойством: если одно из двух слагаемых равно нулю, то сумма равна другому слагаемому:

a + 0 = a 0 + a = a.  Пример 1. Упростите выражение 136 + (a + 214).

Решение.

Используя переместительно и сочетательное свойства сложения, получаем:

 136 + (a + 214) = 136 + (214 + a) = (136 + 214) + a = 350 + a.

Пример 2. Найдите сумму 7 мин 44 с + 5 мин 38 с.

Решение.

Учитывая, что 1 мин = 60 с, имеем:

7 мин 44 с + 5 мин 38 с = 7 мин + 44 с + 5 мин + 38 с = (7 мин + 5 мин) + (44 с + 38 с) = 12 мин + 82 с = 12 мин + 60 с + 22 с = 12 мин + 1 мин + 22 с = 13 мин 22 с.