Тема урока: Теорема о трех перпендикулярах (вводный урок – 2 ч)

Тема урока: Теорема о трех перпендикулярах

(вводный урок – 2 ч)

Цель урока:

обучающая:

·       Изучить теоретический материал по теме, облегчить обучающимся понимание содержания теоремы, обосновать необходимость теоремы о трех перпендикулярах;

·       Сформировать видение изученной закономерности в различных ситуациях: при решении задач на доказательство или задач, требующих найти численное (буквенное) значение, какого – либо элемента;

·       Учить умению читать чертеж;

развивающая:

·       Способствовать развитию общения как метода научного познания, аналитико-синтетического мышления, смысловой памяти и произвольного внимания;

·       Развивать навыки исследовательской деятельности (выдвижение гипотез, анализ и обобщение полученных результатов).

воспитательная:

·       Развивать у учащихся коммуникативные компетенции (культуру общения, умение работать в группах, элементы ораторского искусства);

·       Способствовать развитию творческой деятельности учащихся, потребности к самообразованию.

Оборудование:

1. Слайды по теме «Теорема о трех перпендикулярах»;

2. Каркасная модель чертежа к теореме;

3. Карточки с задачами.

4. Мультимедийное оборудование.

5. Экран.   

6. Компьютер.           

План урока

Ход урока

Урок ведет учитель совместно с консультантом (сильным учеником).

j Разминка. Математический диктант.

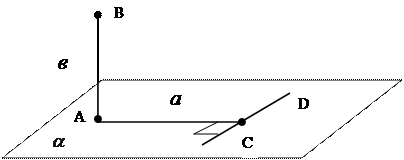
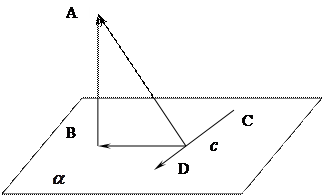
Задание: Перечислите и запишите в тетради названия элементов (отрезков) чертежа, если АВ  (смотрите Рис. 1).

                                                Ответ:  АВ – перпендикуляр;

                                      ВС – наклонная;

Рис. 1

Дополнительные вопросы:

1)    Какой формулой связанны между собой перечисленные отрезки?

(Ответ:  - теорема Пифагора).

2)    Чему равно ВС, если АВ = 3 см, АС = 4 см.? (Ответ: 5 см.).

k Постановка перед учащимися проблемы.

Задача: Через конец А отрезка АВ длины «в», проведена плоскость, перпендикулярная отрезку. И в этой же плоскости проведена прямая. Найти расстояние от точки В до прямой, если расстояние от точки А до прямой равно «а»

Исследование задачи.

1) Рассматривается модель чертежа к теореме из спиц (карандашей), ярко окрашенных, чертеж приводиться на слайде (Рис. 2);

2)    По частям разбирается задача.

а) дан отрезок АВ = в, он перпендикулярен плоскости:

б) в плоскости проводиться прямая, назовем ее СD:

в) по условию задачи известно расстояние от точки А до прямой СD.

! Очень важно именно здесь разобраться, что такое расстояние от точки до прямой на плоскости. Желательно на спицах (карандашах) показать это расстояние, предварительно вспомнив определение: «Расстояние от точки до прямой, есть перпендикуляр, проведенный из этой точки на прямую».

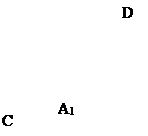
Теперь нужно выяснить, сколько перпендикуляров на чертеже (два: АВ и АА₁) и чему ровно АА₁? (АА₁=а).

г) по условию задачи, необходимо найти расстояние от точки В до прямой СD. Наступил очень важный момент – тот момент, ради которого проводиться этот урок. Необходимо провести перпендикуляр из точки В на прямую СD. На спицах (карандашах) консультант – помощник показывает модель:

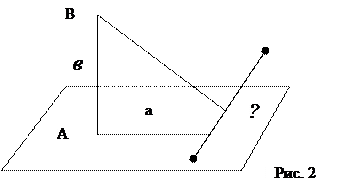
Создается проблемная ситуация: куда пойдет перпендикуляр из точки В?  Где будет находиться его основание на прямой СD?

Выясняются мнения учащихся. Интуитивно некоторые из них догадываются, что основание перпендикуляра, опущенного из точки В на прямую СD, должна находиться в точке А₁.

Но как это доказать?

«Знаем ли мы какую-нибудь теорему, подтверждающую эту догадку?» - спрашивает преподаватель, и продолжает: - «Нет, еще не знаем, а значит, и задачу решить не сможем, пока не изучим нужную теорему. Сегодня мы познакомимся с такой теоремой. Но сначала еще раз вспомним, как называются отрезки АА₁ и предполагаемый отрезок ВА₁. (АА₁ – проекция наклонной ВА₁.; а ВА₁. – наклонная).

Выясним также, сколько перпендикуляров получилось на чертеже (на модели).

(Три: АВ, АА₁., ВА₁.).

На модели ВА₁. – спица (карандаш) желтая, а как только убедились в том, что перпендикуляр, опущенный из точки В, проходит через точку А₁., поменяем желтую спицу на синюю.

l Изучение теоремы.

Обучающимся предлагается сформулировать теорему «О трех перпендикулярах». Консультант – помощник помогает сформулировать теорему с помощью модели и наводящих вопросов. Предлагаются альтернативные варианты формулировки теоремы. Затем учитель предоставляет слово любителям математики, которые дома подготовили свои варианты формулировки и доказательства теоремы. Они поочередно выходят к доске. Обучающиеся их слушают внимательно и выбирают тот вариант, который больше понравился.

Первый выступающий.

Теорема формулируется следующим образом:

Прямая, проведенная на плоскости через основание наклонной перпендикулярно ее проекции, перпендикулярна и самой наклонной.

Доказательство.

1)                          Проведем СА_1. СА₁||АВ по построению, т. к. АВ(Теорема: Если две прямые перпендикулярны к плоскости, то они параллельны). Проведем через АВ и СА₁ плоскость .

2) 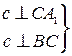                          по Теореме: «Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости».

ч.т.д.

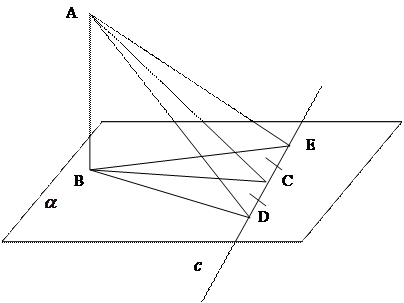
Второй выступающий.

Дано: ; АС – наклонная, ВС – проекция. ВС, АВ.

Доказать: АС.

    Доказательство.

(векторное доказательство)

1)

2) По условию . Значит, . Таким образом получаем: .

ч.т.д.

Третий выступающий.

Дано: ; АС – наклонная, ВС – проекция. ВС, АВ.

Доказать: АС.

Доказательство.

1)    Достроим рисунок так, что 

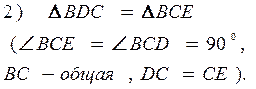
Значит, (как наклонные, имеющие равные проекции).

3) - равнобедренный и, - медиана и высота. .

ч.т.д.

Консультант обсуждает с группой все предложенные варианты доказательства теоремы о трех перпендикулярах.

Учащиеся высказывают свое мнение, они могут выбрать для себя любое доказательство.

После этого учитель вновь обращает внимание ребят на предложенную в начале урока задачу.

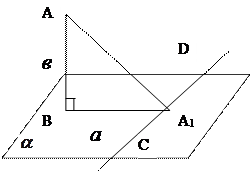mГрупповое решение задачи.

Выясняется, что задача решается в одно действие по теореме Пифагора.

Дано: . .

Найти: Расстояние от точки В до прямой CD

Решение.

1)                          Расстояние от точки до прямой является перпендикуляр. По теореме «О трех перпендикулярах».  - проекция наклонной ВА₁.

2)                          Из , по теореме Пифагора:

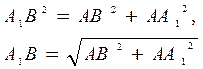
Ответ: Расстояние от точки В до прямой CD равно .

n Закрепление изученного материала.

Предлагаются задачи с числовыми данными. Раздаются индивидуальные карточки с условиями задач

1)

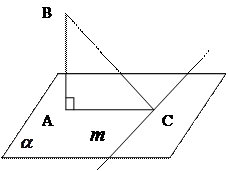Дано:

Найти: АС

Решение.

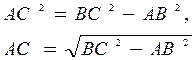Из  по т. Пифагора  далее, подставляя числа

Ответ: 0,3 см.

2) Чертеж тот же.                Дано: АС=6 см., ВС=10 см.

                                             Найти: АВ

Решение

.                                          Ответ: 8 см.

o Практическое применение теоремы о трех перпендикулярах.

(выступления учащихся подготовлены заранее)

Первый выступающий.

Теорема о трех перпендикулярах будет использована при изучении многогранников, когда появиться необходимость в изображении угла между боковой гранью пирамиды и ее основанием.

В будущем узнаем, что угол между боковой гранью пирамиды и ее основанием измеряется линейным углом.

Разберем на примере решения задачи, как построить линейный угол двугранного угла.

Задача: В правильной треугольной пирамиде боковые грани наклонены под углом . Изобразить этот угол (см. рисунок).

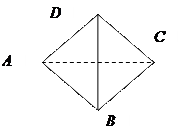
Не будем вдаваться в определение линейного угла, запомним только: чтобы, построить линейный угол, надо в общую точку общего ребра боковой грани и основания пирамиды провести перпендикуляры. Угол между этими перпендикулярами и есть угол .

Проведем из точки D на сторону BD перпендикуляр DK.

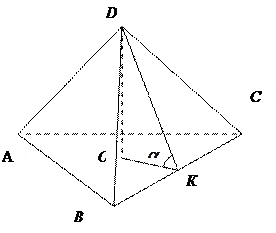Далее из точки D опустим перпендикуляр DO , соединим точку О с точкой К. Будет ли ОК перпендикуляром к ВС?

Да, т. к. ОК – проекция наклонной DK.

По теореме о трех перпендикулярах, .

Второй выступающий.

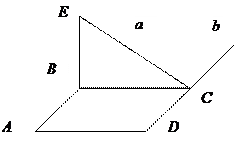Задание: Установить взаимное положение прямых а и в по готовым чертежам.

1.     ABCD – квадрат

BEABCD                                                                   Ответ: .

2. 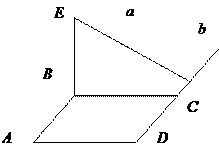    ABCD – квадрат

BEABCD                                                                        Ответ:

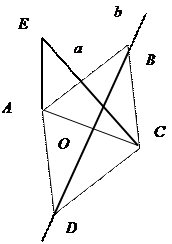3.     ABCD – ромб

АEABCD                                                                         Ответ: .

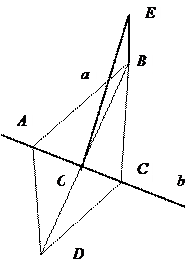4.     ABCD – ромб

BEABCD                                                                         Ответ: .

p Самостоятельная работа

В конце урока предлагается самостоятельная работа по изученному материалу.

Карточки составлены дифференциально – трехуровневые: А, В, С. Ребята выбирают любой уровень. (На карточке указан уровень и номер). Либо решают задачи из разных уровней. Обязательно необходимо решить три любых задачи, остальные задачи решаются дома и сдаются на проверку учителю.

ˆПодведение итогов урока.

Учитель предлагает обобщить учащимся весь теоретический материал, используемый на уроке и решить задачу, которая продемонстрирует успех изучения теоремы о трех перпендикулярах. Выставляются оценки за урок.

Задача.

Дано: AD ┴ (ABC), < BAC = 62º, < ACB = 28º.

Каково взаимное расположение прямых СВ и BD ? Ответ обоснуйте.

‰ Домашнее задание

Учащиеся записывают задание.  ДЗ: №145, №143, №140, п.19,20.

Список используемой литературы.

1.     Геометрия, 10-11: Учебник для общеобразовательных учреждений/ Л. С. Атанасян, В. Ф. Бутузов, С, Б. Кадомцев и др.- М.: Просвещение, 2020.

2.     А. П. Ершова, В. В. Голобородько. Самостоятельные и контрольные работы по геометрии для 10 класса. – М.: Илекса, 2018

3.     Геометрия. 10-11 кл.: Учебник для общеобразовательных учреждений/ Шарыгин И. Ф.- М. Дрофа, 2000.

4.     Лоповок Л. М. Факультативные задания по геометрии для 7-11 классов: Пособие для учителя. - К.: Рад. Шк., 1990.

Задачи для самостоятельной работы.

Уровень А

1. АВ – перпендикуляр к плоскости, АС – наклонная, ВС – ее проекция на плоскость, CD – прямая на плоскости, перпендикулярная прямой ВС. Почему угол ACD – прямой?

2. АВ – перпендикуляр к плоскости, АС – наклонная, ВС – ее проекция на плоскость, CD – прямая на плоскости, перпендикулярная прямой АС. Почему угол ВCD – прямой?

3. На плоскости взяты прямая а и точка А вне ее. Из точки А на прямую а опущен перпендикуляр АВ. Из точки А к плоскости восстановлен перпендикуляр АС. Точку С соединим с точкой В. Сделайте соответствующий чертеж. Укажите все полученные прямые углы. Дайте основание ответу.

Уровень В

1. Угол С треугольника АВС – прямой. AD – перпендикуляр к плоскости треугольника АВС. Докажите, что треугольник BCD – прямоугольный.

2. АВСD – квадрат диагонали которого пересекаются в точке Е. АН – перпендикуляр к плоскости квадрата. Докажите, что прямые НЕ и BD перпендикуляры.

3. Из вершины А квадрата ABCD со стороной 16 см., восстановлен перпендикуляр АЕ длиной 12 см. Докажите, что треугольник ВСЕ – прямоугольный. Найдите его площадь.

4. Из центра О квадрата ABCD со стороной 18 см. к его плоскости восстановлен перпендикуляр ОМ длиной 12 см. Найдите площадь треугольника АВМ.

5.     Отрезок АМ перпендикулярен плоскости треугольника АВС и имеет длину 24 см. Найдите расстояние от точки М до прямой ВС, если АВ = АС = 20 см., ВС = 24 см.

6.     В правильном треугольнике АВС точка О – центр. ОМ – перпендикуляр к плоскости АВС. Найдите расстояние от точки М до стороны АВ, если АВ = 10 см., ОМ = 5 см.

Уровень С

1. Из вершины А прямоугольного треугольника АВС (  - прямой) к плоскости треугольника проведен перпендикуляр АК. Докажите, что прямые КВ и ВС взаимно перпендикулярны.

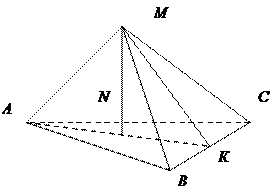2. МАВС – пирамида, , АК – высота . Докажите, что МК – высота грани МВС (см. чертеж).

3. Из вершины С правильного треугольника АВС со стороной 10 см. проведен к его плоскости перпендикуляр СМ длинной 6 см. Вычислить расстояние от точки М до стороны АВ.

4. В равнобедренном треугольнике CEH точка А – середина основания EH. Из точки С к плоскости треугольника проведен перпендикуляр СК. Докажите, что прямые АК и ЕН взаимно перпендикулярны.

5.     Катеты прямоугольного треугольника АВС 15 см. и 20 см. Из вершины прямого угла С проведен отрезок СD, перпендикулярный плоскости этого треугольника, CD = 35 см. Найти расстояния от точки D до гипотенузы АВ.

6.     Доказать, что если точка равноудалена от всех сторон многоугольника, то она проектируется на его плоскость в центр вписанного круга.