Тема урока: "Заключительное повторение курса геометрии 10 – 11 классов. Конус"

Тема урока: "Заключительное повторение курса геометрии

10 – 11 классов. Конус"

“Вдохновение нужно в геометрии, как и в поэзии”. 

(АС.Пушкин)

Цель урока: Систематизация и углубление знаний по теме "Конус". Повысить интерес к геометрии, решая нестандартные задачи.

Образовательная:

o    отрабатывать знания основных понятий, определений, теорем и умения применять эти знания при решении задач различных по содержанию и уровню сложности.

Развивающая:

o    развивать логическое мышление, умение сравнивать, обобщать, классифицировать;

o    развивать и совершенствовать умения применять накопленные знания в измененной ситуации, делать выводы и обобщения.

Воспитательная:

o    воспитывать ответственность за результат своего труда.

Тип урока: урок обобщения и систематизации знаний.

Методы обучения: практический (устный опрос, тестовая проверка, самопроверка и взаимопроверка).

Формы организации урока: индивидуальная, фронтальная, парная.

Оборудование: средства ТСО, презентация, дидактический материал (тесты, самостоятельная работа)

Ход урока

I. Организационный момент (3 мин)

II. Актуализация знаний (10 мин)

            Фронтальный опрос: (слайд 4)

1.      Дать определение конуса.

2.      Как можно получить эту фигуру?

3.      Чему равна S_б и S_n конуса?

4.      Что лежит в основании конуса?

5.      Что получится при вращении прямоугольного треугольника вокруг гипотенузы?

6.      Назовите элементы конуса и покажите их на чертеже. (слайд 5)

7.      Решить задачу по готовому рисунку. (слайд 7)

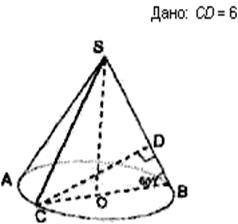SO-высота.

Найти площадь боковой поверхности.

Решение:

1)      В ∆CDB: ∠CDB = 90⁰, ∠DBC = 60⁰ ⟹ Sin∠DBC =  ⟹  ⟹

CB = , CB = d ⟹ r = .

2)      В ∆SOB:   ∠COB = 90⁰,  ∠SBO = 60⁰   ⟹  Cos∠DBC =  ⟹     ⟹     SB =  = l.                                       S_бок=  ⟹ S_бок=

ТЕСТ  (слайд 9)

Проверить ответы учащихся по вариантам. (слайд 10)

III. "Конусы в нашей жизни" (7 мин) (слайд 11)

Вопросы ко взводу:

-        Установите связь между картиной Шишкина "Корабельная роща" и геометрическим телом, которое называется "конус".

Ответ: Конус в переводе с греческого языка означает "сосновая шишка", а на картине Шишкина изображен сосновый лес.

-        Где еще в природе встречаются конусы?

Ответ: корпус шариковой ручки, конец стержня шариковой ручки, горы, елки, стволы деревьев, ракета для полёта в космос, маяк, громоотводы, морские ракушки, сосульки зимой, детские пирамидки из колец, мы используем ведра, имеющие форму усеченного конуса; крыши старинных замков похожи на конусы; для переливания жидкостей мы берем воронку, которая также имеет форму усеченного конуса

IV.  Решение задач на практическое применение (7 мин):

Как вы сейчас узнали: конус очень часто можно встретить в нашей жизни. А теперь нам

предстоит решить задачи с практическим применением.

По статистике на Земле ежегодно гибнет от разрядов молний 6 человек на 1 000 000 жителей (чаще в южных странах). Этого бы не случалось, если бы везде были громоотводы, так как образуется конус безопасности. Чем выше громоотвод, тем больше объем такого конуса. Некоторые люди пытаются спрятаться от разрядов под деревом, но дерево не проводник, на нем заряды накапливаются и дерево может быть источником напряжения.

Задача 1. "Молниеотвод". (слайд 15)

Вычислите высоту молниеотвода, если радиус "защищенного" круга 50 м, а угол между молниеотводом и образующей конуса безопасности 60 (самостоятельная работа на местах с последующей проверкой).

Решение:

tg 60° =  ;  tg 60⁰ = √3 ≈ 1,7

h =  ≈ 29,4м

Ответ: 29,4м

А если необходимо вычислить поверхность произвольного конуса, высота и радиус которого не доступны для непосредственного измерения.

Вопросы ко взводу:

-        Как найти радиус?

(измерить окружность основания и разделить на 6,28 = 2);

-        Как найти образующую?

(определить две образующие: перекинув метровую ленту через вершину геометрического тела);

-        Как найти высоту? (определить по теореме Пифагора).

Задача 2: (слайд 16)

Пусть окружность конической кучи камней 12 м (L_окр). Длина двух образующих - 4,6 м (L_бок).

Найти площадь поверхности кучи камней.

Решение.

L_бок = 2l    ⟹  1 =   = 2,3 м

r =   

   ⟹   r =   ≈ 1,9 м

S =  · r  · l = 3,14 · 1,9 · 2,3 ≈ 13,7 м²

Ответ: 13,7 м²

Учитель: При взгляде на коническую кучу камней или песка мне вспоминается старинная легенда восточных народов, рассказанная у А.С. Пушкина в "Скупом рыцаре" (слайд 17). Послушайте её:

"Читал я где-то,
Что царь однажды воинам своим
Велел снести земли по горсти в кучу, -
И гордый холм возвысился,
И царь мог с высоты с весельем озирать
И дол, покрытый белыми шатрами,
И море, где бежали корабли…”

·         Какие ассоциации вызывают у Вас эти стихи? (Холм – это конус).

·         Какой высоты мог быть этот холм?

·         На сколько километров может увеличиться панорама для наблюдения, поднявшегося с подножия холма к его вершине?

На все эти вопросы мы сможем ответить после повторения темы “Объем тел вращения”. Это “задача на будущее”.

V. Самостоятельная работа (10 мин)

VI. Рефлексия (3 мин): (слайд 18)

Каждому суворовцу раздать наклейки трёх цветов (красный,  желтый, зелёный). На листе бумаги они должны наклеить  наклейку, соответствующую их ответу.

Красный цвет –  мне непонятно, что такое конус, как получается это геометрическое тело, как применять формулы для решения конуса и как в жизни можно применить знания, полученные на уроках геометрии.

Жёлтый – мне не совсем понятно, что такое конус, как получается это геометрическое тело, как правильно применять формулы для решения конуса и как в жизни можно применить знания, полученные на уроках геометрии.

Зеленый цвет – мне  понятно, что такое конус, как правильно применять формулы для решения конуса и как в жизни применить знания, полученные на уроках геометрии.

VII. Подведение итогов урока. Домашнее задание (5 мин): (слайд 19)

Итак, вы повторили, как находить элементы конуса, площадь поверхности, применили свои знания в "геометрии на воздухе". Надеюсь, что в дальнейшем теоретические знания, полученные на уроках геометрии, вы сможете успешно использовать в различных жизненных ситуациях.

Выставление оценок.

1.      § 2, п. 61 – 63, §3, п. 81. Повторить формулы решения конуса;

№ 565, № 572.

2.      Из книги для подготовки к ЕГЭ (Д.А. Мальцев):

            № 12, тест 13 – 14;

            № 9, тест 25 – 26;

Литература:

1.Л.С. Атанасян “Геометрия 10-11”.

2. П.И.Алтынов, Л.И.Звавич, А.И.Шляпочник и др. “2600 тестов и проверочных заданий по математике для школьников и поступающих в ВУЗы”.

3. Материалы сайта фестиваля педагогических идей “Открытый урок”.

Скачано с www.znanio.ru